球头铣刀多轴铣削的刀具与工件切触区域实时计算方法

黎柏春,王振宇,杨建宇,王宛山

(1.中国民航大学 航空工程学院,天津 300300; 2.东北大学 机械工程与自动化学院,辽宁 沈阳 110819)

铣削力作为研究铣削过程的基础和前提,近年来很多学者对其进行了研究,而且理论建模和仿真已成为铣削力研究的重要手段[1].铣削力建模和仿真需要以铣削过程的几何信息为基础,包括实时刀具运动状态、切触区域等.其中,刀具与工件切触区域是铣削力模型中确定积分边界的重要依据.尤其对于球头铣刀的多轴铣削,由于刀具的球面形状和刀轴方向改变使得切触情况复杂、多变,其切触区域计算成为相关研究需要解决的首要问题.

Yang等[2]提出了一种基于实体修剪的切触区域求解方法.Taner等[3]提出了一种基于几何投影的切触区域求解方法.Gong等[4]将刀具和工件表示为三角形网格描述的实体后,通过减法布尔运算不断更新工件,确定切触区域.Wei等[5]提出了一种改进的Z-Map离散方法.Inui等[6]设计了基于图形处理器(Graphics Processing Unit,GPU)加速和单向Dexel离散的几何仿真算法,由此确定切触区域.Li等[7]提出了一种计算切触区域的解析方法.魏北成等[8]将球头铣刀多轴铣削过程考虑为一系列的微小斜平面切削,从而确定多轴铣削时的切触区域.Zhu等[9]将平底圆角铣刀多轴铣削的切触区域边界分为3种曲线,由此得到切触区域符号化解析模型.

综合上述研究,切触区域的计算方法可总结为实体仿真方法、离散仿真方法和解析方法.实体仿真方法具有较高的计算精度,但需要大量空间,而且计算效率低,计算100个刀位点耗时数分钟[2],不适用于多轴铣削复杂曲面.离散仿真方法降低了对存储空间的需求,但存在计算精度和计算效率的平衡矛盾,一般只适用于三轴铣削的情况[8].解析法具有较好的计算精度和计算效率,但切触区域边界模型往往比较复杂,尤其是球头铣刀多轴铣削复杂曲面时,难以建立准确的边界模型,因此,该方法只适用于工件轮廓可用数学模型描述的情况,不适用于铣削表面二次铣削以及多轴铣削复杂曲面的情况.鉴于此,本文针对球头铣刀多轴铣削复杂曲面,提出一种实时计算刀具与工件切触区域的方法.

1 切触区域实时计算的基本流程

切触区域实时计算方法的总体流程如图1所示,该方法主要包括以下关键环节:① 从数控程序中提取铣削工艺参数和刀具轨迹信息,计算每齿进给量,并以此为基本长度离散刀具轨迹一系列位置和位姿数据.② 根据刀具几何参数,构建相距每齿进给量大小的两相邻刀位的刀具扫描体模型.③ 体素化工件和刀具扫描体模型,以便将复杂的三维空间布尔运算转化为一维布尔运算.④ 进行布尔运算,更新工件的体素化数据,并标记当前更新的工件表面数据.⑤ 从当前更新的工件表面数据中筛选出切触区域点数据,进行实时重建渲染.

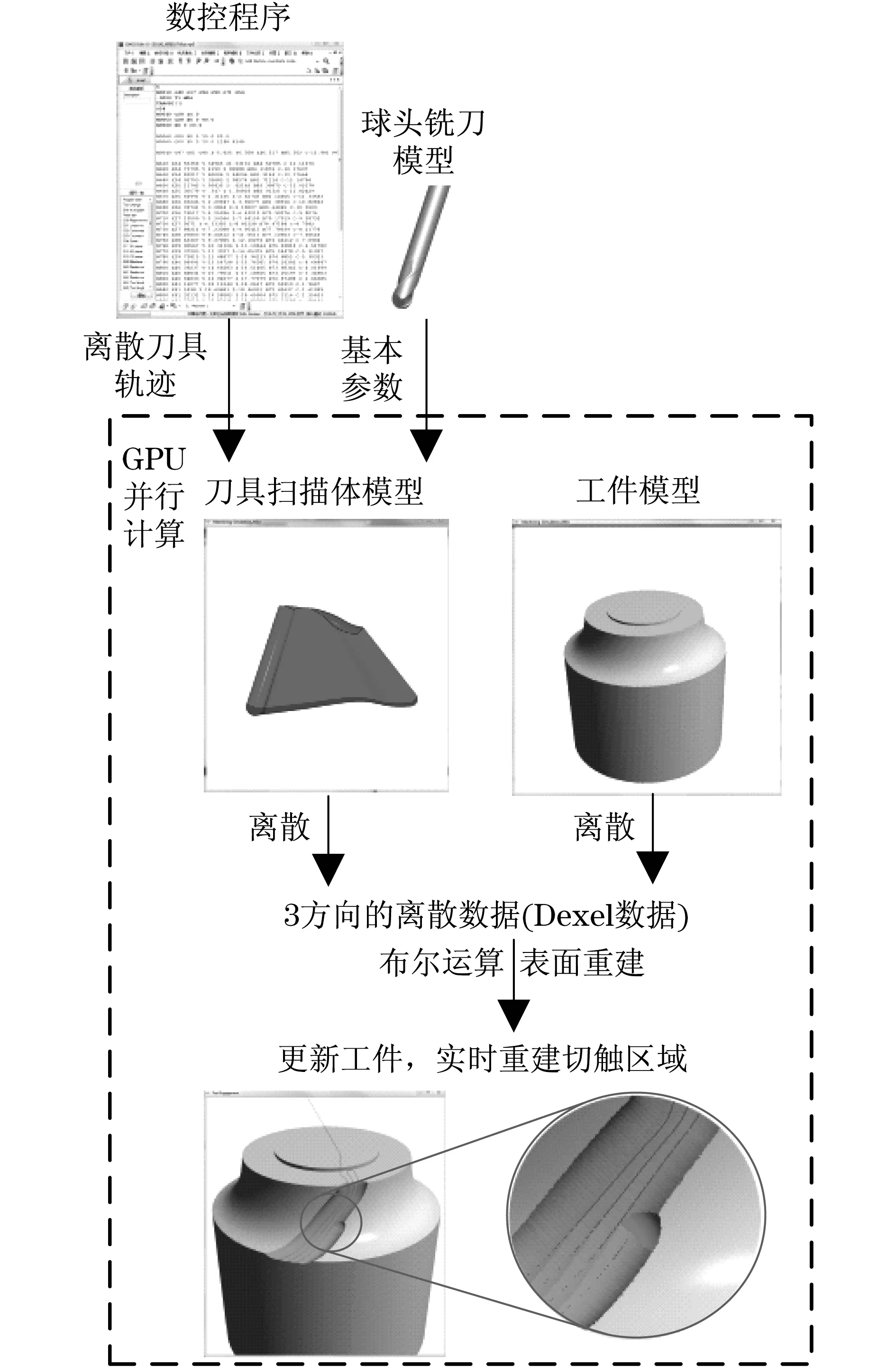
图1 总体流程Fig.1 Flow diagram

为了保证在高精度离散前提下,提高切触区域计算效率,相关计算主要由GPU并行计算实现.前期工作[10-11]已完成刀具扫描体建模和模型体素化研究.

2 面向切触区域实时计算的铣削加工几何仿真

2.1 刀具位置和位姿

为了获得刀具位置和位姿,需要模拟数控系统的译码和插补运算.模拟数控系统的译码就是将数控程序读取到内存后,进行分类处理和数值提取,插补就是对数值进行分类插值.因此,可设计译码和插补的算法流程,如图2所示.

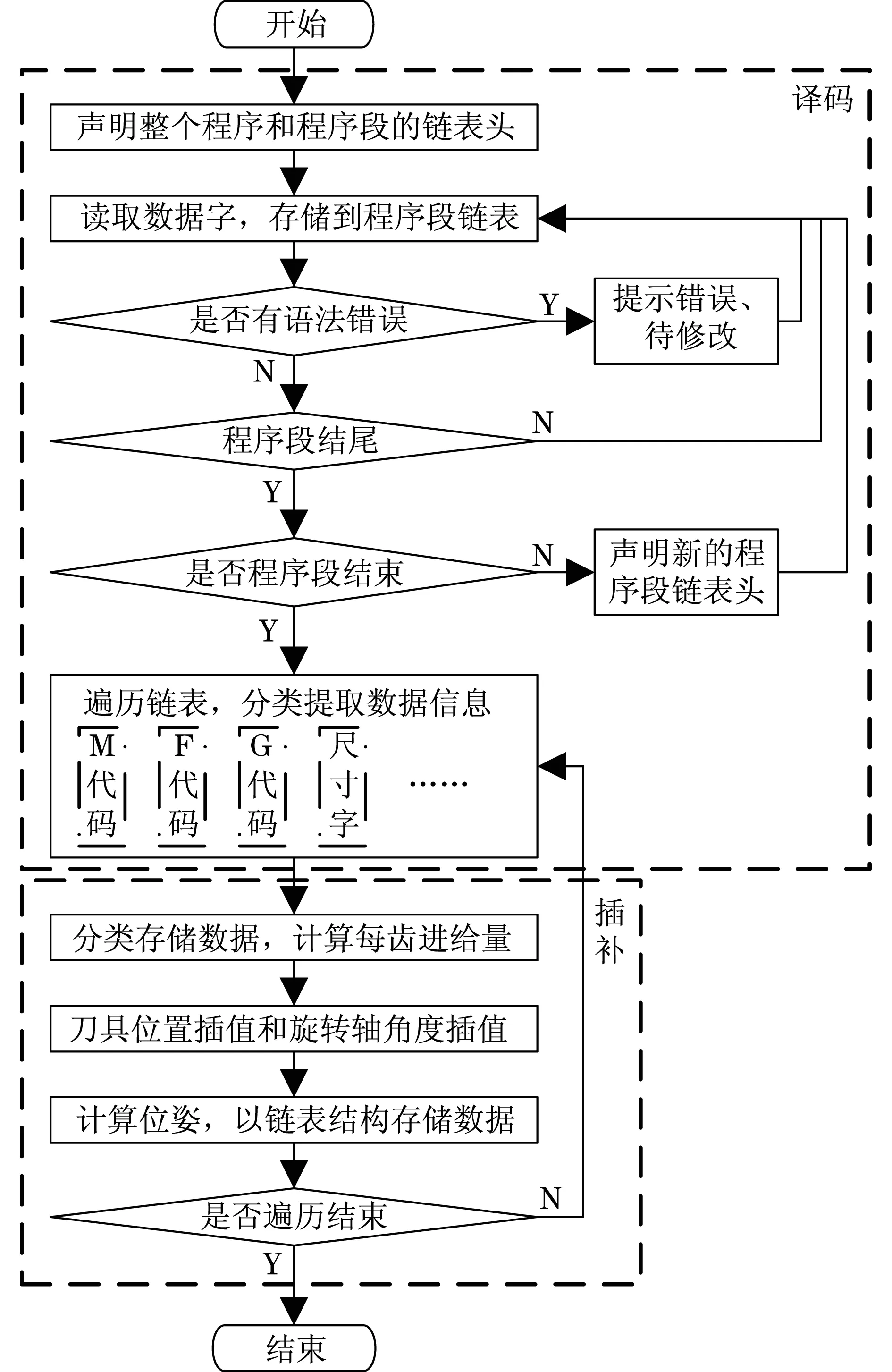
图2 数控程序译码和插补的模拟算法Fig.2 Algorithm for simulation of decoding numerical control codes and interpolation

不同数控程序的行数和程序段长度不同,译码时所需内存存储空间动态多变.为此,图2的算法采用链表嵌套链表的数据结构为其动态分配存储空间,即将程序段以数据字为单元通过链表数据结构形式存储,而且程序段之间也使用链表形式有序地组织为一体,其逻辑结构如图3所示.

从数控程序中获得刀具位置和机床旋转轴角度后,还需要对其以每齿进给量为基本长度进行插值,并根据旋转轴角度计算刀具位姿.数控系统实现多轴铣削时刀位和旋转轴角度插补一般采用线性插值方式[12],据此可直接写出刀尖位置的插值表达式为

(1)

图3 数控程序存储的逻辑结构示意图Fig.3 Diagram of logical constructs for storing numerical control codes

式中:pi-1,pi为插值得到的相邻刀尖位置坐标;f为进给速度(mm/min);n为主轴转速(r/min);Nf切削刃数;pj为从数控程序提取的离散刀具位置;条件1为pi-1∈[pj-1pj]且pi∈[pj-1pj];条件2为pi-1∈[pj-1pj]且pi∈[pjpj+1].

刀具位姿与机床结构形式密切相关,文中以回转摆动形式的五轴机床为例,如图4所示.

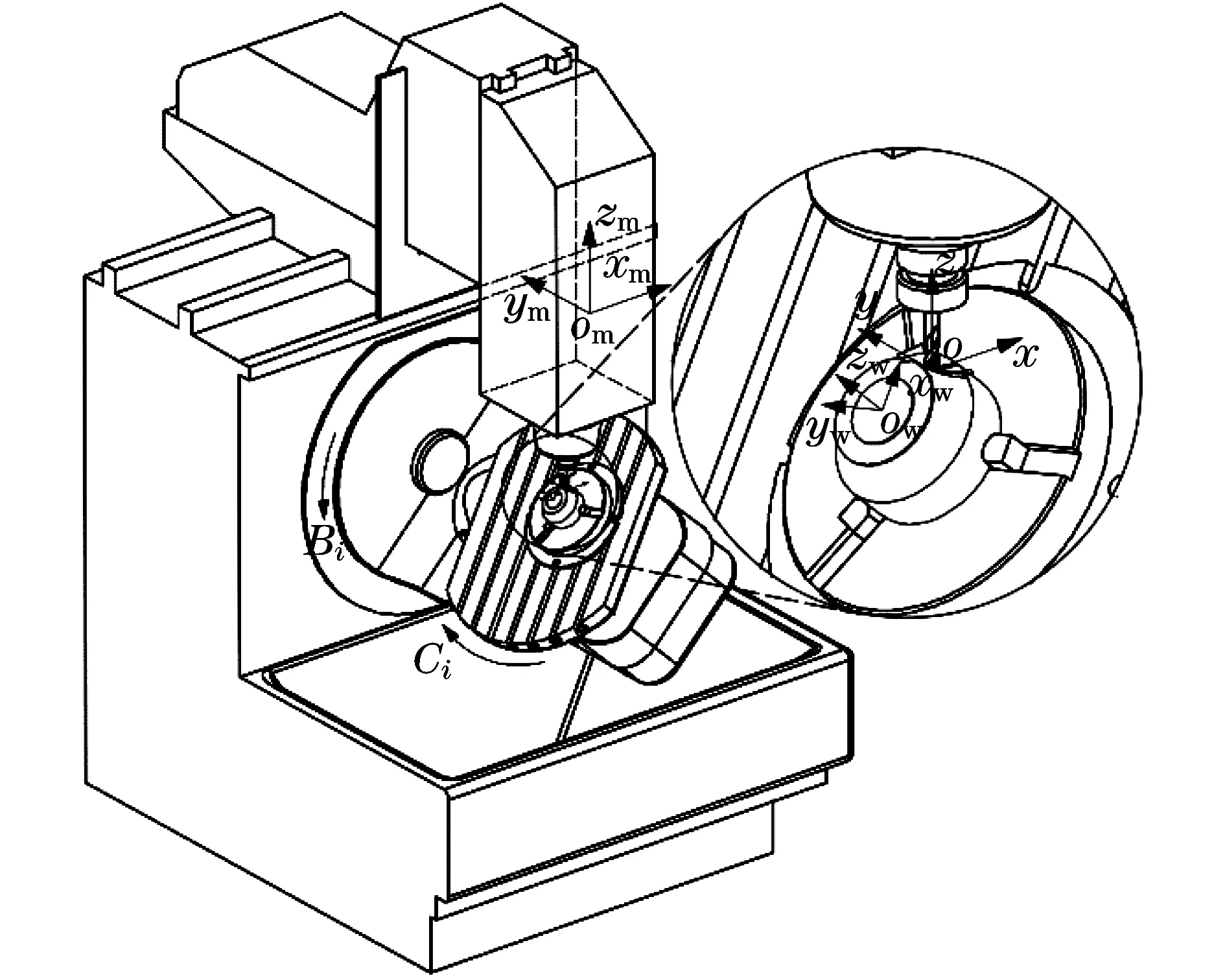
图4 五轴机床Fig.4 5-axis machine tool

根据线性插值可得到刀位pi对应的旋转轴角度Bi和Ci为

(2)

(3)

式中:Bj和Cj分别为pj对应的B,C旋转轴角度,从数控程序中提取得到.

图4中,om-xmymzm为机床坐标系,ow-xwywzw为工件坐标系,o-xyz为刀具坐标系.其中,刀具坐标系o-xyz以刀尖为原点,刀轴方向为z轴正方向,进给方向在垂直于z轴平面内的投影方向作为x轴正方向,y轴正方向则由笛卡尔坐标系右手定确定.根据图4坐标系和B,C旋转轴运动关系,可写出刀具位姿在工件坐标系下的矢量形式为

(4)

2.2 GPU加速的布尔运算

插值获得刀具位置和位姿后,利用文献[10]的方法可实时建立刀具扫描体模型.为了能够计算每齿进给量的切触区域,必须将每相邻的两个刀具位置和位姿构建为独立的刀具扫描体模型.然后,利用文献[11]的方法,将工件模型和刀具扫描体模型离散为3方向的Dexel体数据,进行布尔运算.

为了实现布尔运算的GPU并行加速,利用着色语言GLSL控制顶点着色器和transform feedback步骤实现在GPU上的布尔运算.具体思路是将工件的Dexel数据以顶点属性的形式存储到transform feedback对象申请的显卡缓存区,需要存储的每个Dexel数据主要包括网格坐标、长度坐标、法向量和切削状态标识符;而刀具扫描体的Dexel数据则以颜色纹理形式存储,如图5所示.纹理坐标可作为Dexel数据的网格坐标,因此,颜色纹理只需存储每个Dexel数据的长度坐标和法向量.

工件、刀具扫描体离散后的布尔运算和工件数据更新过程可分为6类,如图6所示.为了方便表达,将工件Dexel数据两端的长度坐标分别记为bw和tw(沿Dexel投射方向,bw为近端,tw为远端),对应的表面法向量记为ξ1和ξ2.将扫描体Dexel数据两端的长度坐标分别记为bc和tc,对应的表面法向量记为n1和n2.

图5 刀具扫描体到颜色纹理的映射示意图Fig.5 Schematic diagram of mapping cutter swept volume into color texture

图6 布尔运算和工件数据更新Fig.6 Boolean operation and workpiece update

(1) 图6(a)中bc>tw,此时工件的Dexel线段未被切削,无更新.

(2) 图6(b)中bw>tc,此时工件的Dexel线段未被切削,无更新.

(3) 图6(c)中tc>tw>bc>bw,此时工件Dexel线段的远端被切削,即更新tw为bc,更新ξ2为-n1.

(4) 图6(d)中tw>tc且bc>bw,此时工件Dexel线段的中间部分被切削,生成2个新Dexel线段.

(5) 图6(e)中tc>tw且bw>bc,此时工件Dexel线段被全部切除.

(6) 图6(f)中tw>tc>bw>bc,此时工件Dexel线段的近端被切削,即更新bw为tc,更新ξ1为-n2.

根据数据存储、布尔运算和工件数据更新,设计基于GPU并行计算的布尔运算算法,如图7所示.

3 切触区域实时重建

图7所述算法能够标记每次新生成的点集,但布尔运算是工件模型和刀具扫描体模型之间的布尔运算,因此，标记的离散点集并非完全位于刀具表面,不能直接作为构建切触区域的点集.为此,通过点和球心(球头部分的球心)距离筛选刀具切触区域点集.假设布尔运算新生成的任意点坐标为(wx,wy,wz),由前述可知该坐标为工件坐标系下坐标,为了计算方便将其变换到刀具坐标系下为

(5)

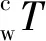
(6)

其中，nx为刀具坐标系x轴正方向单位矢量

(7)

nf为刀具瞬时进给方向的单位矢量

(8)

球心在刀具坐标系下坐标为(0, 0,R),R为刀具半径.由式(5)计算得到的坐标和球心坐标,在考虑离散误差情况下，可将刀具切触区域点集表示为

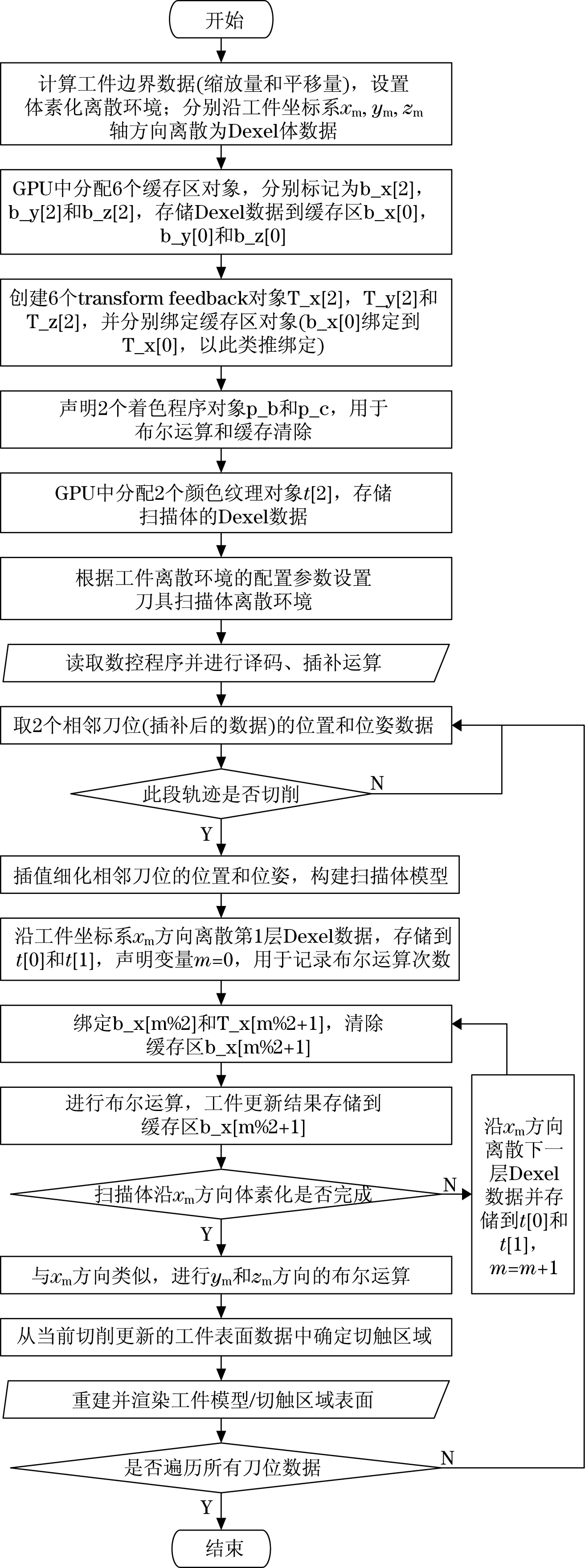
图7 GPU加速的布尔运算算法Fig.7 Algorithm of Boolean operation based on GPU acceleration

(9)

式中:δ为三维模型的离散精度.

在Dexel结构中，点数据包括点的位置坐标和表面法向量.因此,可以通过在点位置坐标中心创建基本图元重建表面,例如：三角面片、四边形等.但此时存在基本图元之间融合问题,不能实现基本图元无缝连接,形成光滑表面.为此,需要对点位置坐标进行微小调整,然后以各点为中心创建以离散精度δ为边长的四边形图元,其原理如图8所示.

图8 切触区域表面重建原理Fig.8 Surface reconstruction of cutter-workpiece engagement

点(cx,cy,cz)调整后的新点为

(10)

其中，(cx1,cy1,cz1)和(cx2,cy2,cz2)为

此外,渲染重建表面时，光照计算使用Dexel中的表面法向量cξ,以保证表面显示的光滑连续.

4 仿真分析和验证

为验证文中方法的可行性,利用C++语言、OpenGL 4.5图形接口和GLSL着色语言开发实现切触区域计算的相关算法,并通过模拟叶轮开粗铣削过程实时计算切触区域.叶轮开粗铣削过程选择半径为R=4 mm的球头铣刀作为刀具,主轴转速6 000 r/min,进给速度3 200 mm/min,其仿真结果如图9所示.由图9可以看出,文中方法适用于多轴铣削复杂曲面的切触区域仿真计算,且切触区域光滑连续,具有良好的渲染显示效果.

图9 切触区域的仿真计算结果Fig.9 Simulation results of cutter-workpiece engagement

为了验证文中方法的准确性,通过三维建模软件中实体布尔运算功能(实体仿真方法)，计算叶轮开粗铣削过程中某个刀位点的切触区域,并将其与文中方法的计算结果进行对比分析.为了便于比较,将切触区域沿刀具坐标系z轴负方向投影,如图10所示.

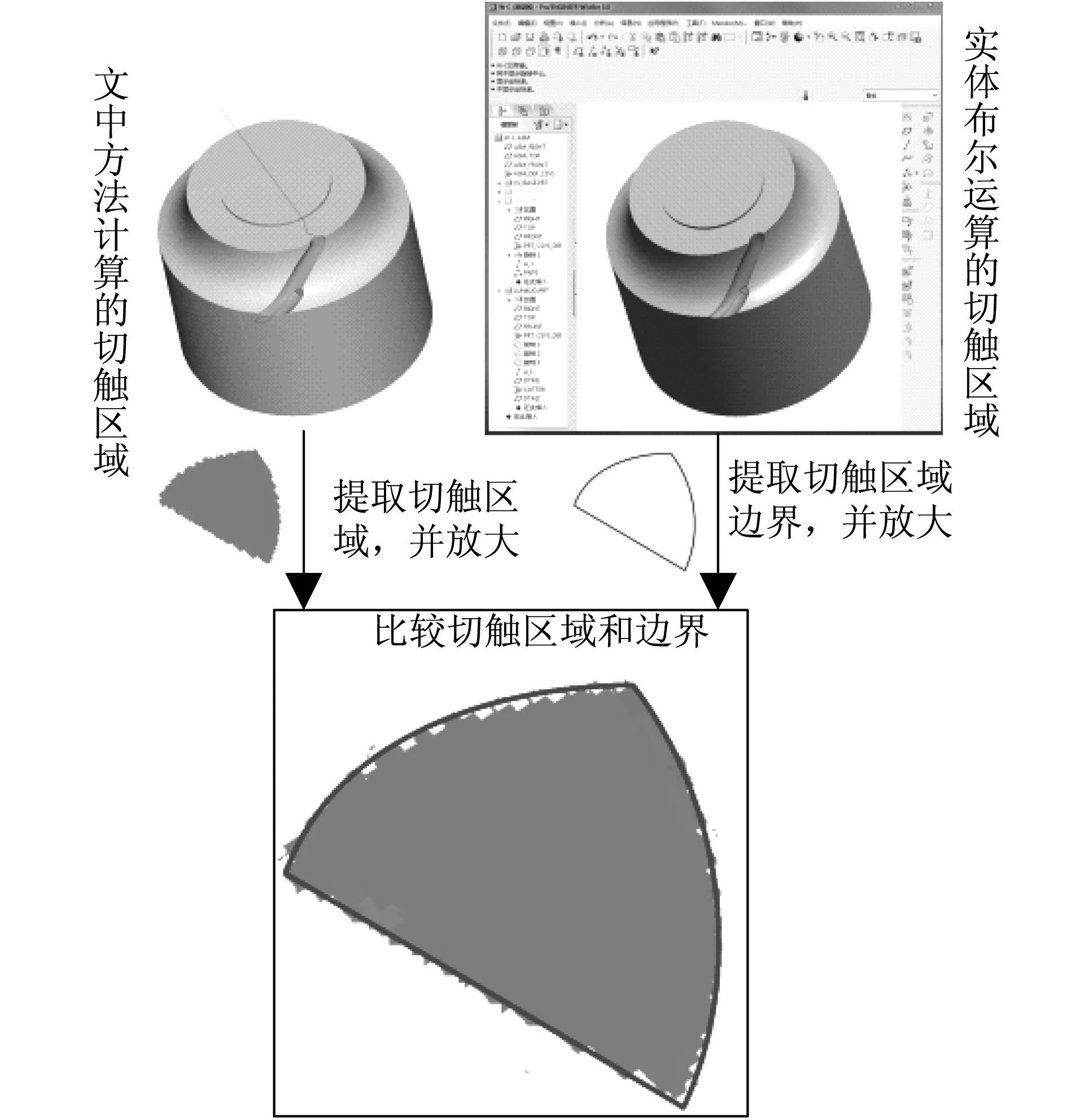
图10 切触区域仿真结果对比分析Fig.10 Comparison and analysis of simulation results of cutter-workpiece engagement

由图10可以看出：实体布尔运算计算得到切触区域具有清晰轮廓、较高精度,可作为验证文中方法的依据.但其计算过程复杂、效率低,需要大存储空间,实用性较差.此外,文中方法和实体布尔运算方法分别计算得到的切触区域具有较高吻合度,且偏差极小,从而验证了文中方法的准确性.

对于文中方法的实时性,在普通PC机(Intel Core i3-7350K 4.2 GHz,内存8 GB,显卡Nvidia GeForce GTX 970)上仿真计算叶轮开粗铣削切触区域时，帧率可达40 帧/s左右,即每分钟大约能计算2 400个刀位点的切触区域,具有良好的实时性.

5 结论

结合前期研究成果,以3方向离散方法和GPU并行计算为基础,提出了针对球头铣刀多轴铣削复杂曲面的切触区域实时计算方法.给出了刀具与工件切触区域实时计算的基本流程,设计了模拟数控程序译码和插补过程的算法流程,推导了插值计算刀具位置和位姿的表达式,设计了GPU加速下面向切触区域计算的工件和刀具扫描体布尔运算算法,给出了并行重建切触区域的方法.

为了验证文中方法和相关论述,开发实现了切触区域计算的相关算法/方法.以典型的叶轮开粗铣削为例,进行切触区域仿真计算,并与三维建模软件中的实体布尔运算结果进行对比分析.相关结果表明：文中方法不仅具有较好的可行性和良好的实时性,而且计算的切触区域具有较高准确度和精度.因此,文中的切触区域计算方法具有较强的实用性和应用价值,对球头铣刀多轴铣削的进一步研究和应用具有重要意义.