基于模型控制的并联机构机器人腿简化建模与辨识方法研究
2019-12-31史琼艳谢小敏
史琼艳,谢小敏
(1.常州机电职业技术学院 机械工程学院,江苏 常州 213164; 2.河海大学 机电工程学院,江苏 南京 210098)
腿式机器人与轮式机器人不同,腿式机器人可以执行多种工作,比如在复杂的环境中爬梯子和克服障碍等[1].近几年大量的专家学者在腿式机器人上进行了大量的研究以提高机动性.在腿式机器人中,更多的研究重点放在四足机器人的应用上,例如在不平坦的地形中进行救援和承载负重,因为四足机器人的特性确保了腿式机器人具有更多的静态稳定性[2].
文献[3]研究了平面双滑块机构的2DOF并联机器人,计算得到机器人驱动力方程,利用Matlab及ADAMS软件验证模型的有效性.文献[4]研究3-PRR并联机器人机构运动学,研究3-PRR并联机器人运动特性,并进行数学建模,利用ADAMS仿真软件验证建模的合理性.文献[5]深入研究6PUS-UPU并联机器人运动学以及动力学,基于拉格朗日方程建立该并联机器人运动学模型,对该模型进行模糊辨识,为了实现驱动力的优化对冗余分支控制器进行设计,最后在Matlab及ADMAS中验证控制效果.
并联结构在运动学及动力学上有强耦合性[6],通常可以用传统的基于模型的控制器进行并联机器人全动态建模控制[7].虽然这种方法可以减少建模误差,但在动力学计算方面非常复杂.此外,在串联机器人中设计基于模型的控制器的一般方法并不适用于并联机器人.对此,本文提出并联机构机器人腿的简化建模和控制策略,构造并联2自由度机器人腿简化模型,给出了简化模型动力学方程,利用RLS法识别简化模型动力学参数,对比PD控制器和非线性控制器控制策略,使用ADAMS/Matlab进行简化模型的参数识别及两种不同类型控制器控制效果验证.结果表明,所提出的建模方法在仿真软件中实现系统识别和基于模型控制的有效性.
1 系统概述及建模
1.1 2自由度机器人腿模型
本文研究的并联机器人腿是一种用于在非结构化环境下进行运动的液压机器人腿平台.该平台具有2个自由度,每个自由度都有液压缸和伺服阀驱动[8].
腿部机构设计成用来匹配极坐标中的驱动关节,并且它可以在关节空间中简化为弹簧式倒立摆(SLIP)模型,其中,θr,r分别为二维空间上极坐标的角度和极径.
两个执行器分别进行摆动和径向运动.如果摆动执动器是固定的并且径向运动执行器可以自由运动,那么腿的端点(以r表示)可以沿直线(径向)移动.如果摆动执行器可以自由运动并且径向运动执行器是固定的,则整个关节腿(以θr表示)可以在摆动轴的方向上旋转.为了更好地描述机器人腿在二维空间的运动,引入了图1中的模型,其中,f1,f2分别是执行器1和2产生的力,τ,F分别是对θr和r施加的广义力,L1,L2,L3是相应腿部的长度,φ1,φ2,φ3是相应位置的角度.那时,执行器的作用力(f1,f2)和广义力(τ,f)关系如下[9]:
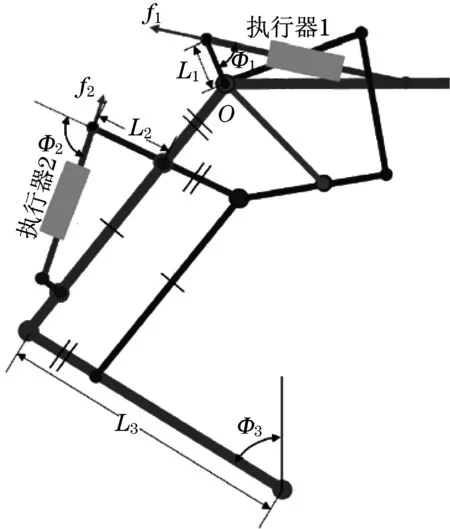
图1 具有运动参数和执行器力的示意图Fig.1 Schematic diagram with kinematic parameters and actuator forces
1.2 基于简化模型的动态建模
为了实现基于模型的控制,这里需要获得模型的动力学和参数.然而,与串联机器人动力学相比,并联机构具有复杂的耦合动力,因此,获得并联机器人的完整动力学方程需要大量的努力和时间.此外,从完整的动力学方程中重写回归矩阵是困难的.本文提出了一个简单的模型,而不是整个并联机构模型.假设这个并联关节腿为2自由度机械手,该机械手只具有一个转动关节和一个移动关节.这个模型能够通过径向及转动方向驱动器独立地进行径向运动以及摆动.
为了简化计算,假设该系统为理想的运动,忽略了作用在机器人上的摩擦力和重力.此外,本文假设坐标系原点固定在地面上.利用拉格朗日公式生成机器人动力学模型,2自由度机器人动力学方程的结果如下:
(5)
(6)
M22=m2
(7)
2 系统识别
2.1 识别模型
获得机器人动力学参数的简便方法是通过计算机辅助设计(CAD)获取设计模型的理论值.然而,由于简化模型与实际模型不同,因此,不可能获得实际参数.本文使用另一种方法获得简化模型参数——系统识别.
传统的系统识别方法主要有以下几个步骤.
步骤1从机器人动力学方程式(3)中定义动态参数,构造一个不随时间变化的回归矩阵.
步骤2将回归矩阵和动态参数从机器人动力学方程中分离出来,重写机器人动力学方程,该方程与动态参数呈线性关系[7].因此,式(3)改为如下:
(8)

定义动态参数如下:
(9)
最终得到回归矩阵如下:
(10)
2.2 识别算法
为了识别系统的动态参数,首先需要确立关节腿的回归矩阵,然后对每次采样周期的输入信号(关节力和力矩)、输出信号(关节位置、速度和加速度)进行测量[10].这时的测量信号可以表示为
其次,利用优化算法对系统的动态参数进行估算.如果选择常用的最小二乘法进行估算,那么参数如下:
(13)
此外,还有其他类型的优化方法用于估算:加权最小二乘法、最大相似估计法(利用傅里叶级数输出满足PE条件的期望轨迹)以及扩展卡尔曼滤波器(EKF)(用于非线性系统中)[12].本研究采用递归最小二乘法(RLS)[13].识别算法如下所示:

首先初始化参数,然后在每个采用时间点测量输入输出值,得到回归矩阵,最后更新估算参数.
3 控制策略定义
并联机器人的控制策略一般有两类,分别为运动学控制及动力学控制策略.为了验证建模方法的有效性,同时获得基于模型控制的名义值,本文使用PD控制器(见图2)和非线性同步控制器(见图3).
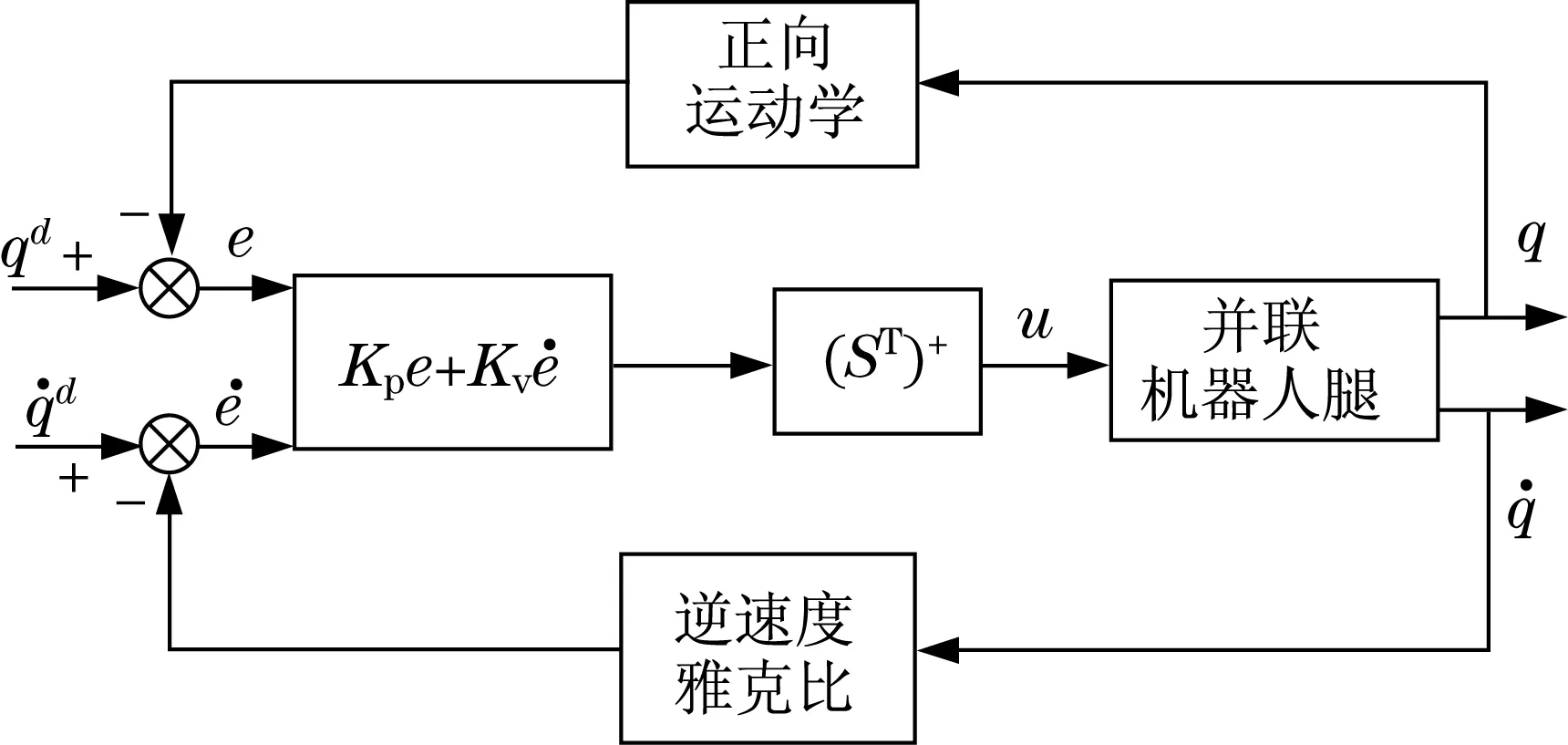
图2 PD控制器框图Fig.2 PD controller block diagram

图3 非线性同步控制框图Fig.3 Nonlinear synchronous controller block diagram
定义末端执行器的期望轨迹如下:
(14)
式中:x,y分别为关节1和2期望轨迹的轮廓.
PD控制器控制输入定义如下:
(15)
式中:KP为比例增益矩阵;Kv为积分增益矩阵;S为末端执行器与关节的速度雅克比矩阵;e为关节误差.
非线性同步控制器控制输入定义如下:
(16)
式中:Kp为比例增益矩阵;Kd为微分增益矩阵;T为耦合误差;S为末端执行器与关节的速度雅克比矩阵;e为关节误差.
4 仿真模拟
本节利用仿真软件Matlab验证上文所提出的建模方法的有效性,同时获得基于模型控制的动态参数值.首先,利用上节中介绍的识别模型和识别算法对简化模型进行系统识别.然后,选择两种不同的控制策略应用于模型控制,比较两者的控制性能.对于动态参数值的获取,使用ADMAS软件来进行动力学模拟.图4为软件中机器人腿模型.

图4 机器人腿的仿真模型Fig.4 Simulation model of robot legs
4.1 动态参数计算
为了将机器人腿系统作为2自由度机械手来进行系统识别,本文首先检查是否满足以下条件,然后启动执行机构进行输入:① 机器人腿应在其运动范围内移动;② 回归矩阵在激励过程中必须满秩(即应满足持续激励条件).其次,以1 ms为时间间隔,测量了2 s内的输入(关节力和扭矩)和输出信号(关节位置、速度和加速度).最后,使用RLS算法估算动态参数.
使用RLS算法估算动态参数的仿真结果如图5所示,式(9)中机器腿动力学参数ρ1,ρ2,ρ3最后收敛到一个恒定值,分别为10.02 kg,-0.412 kg·m以及1.213 5 kg·m2.
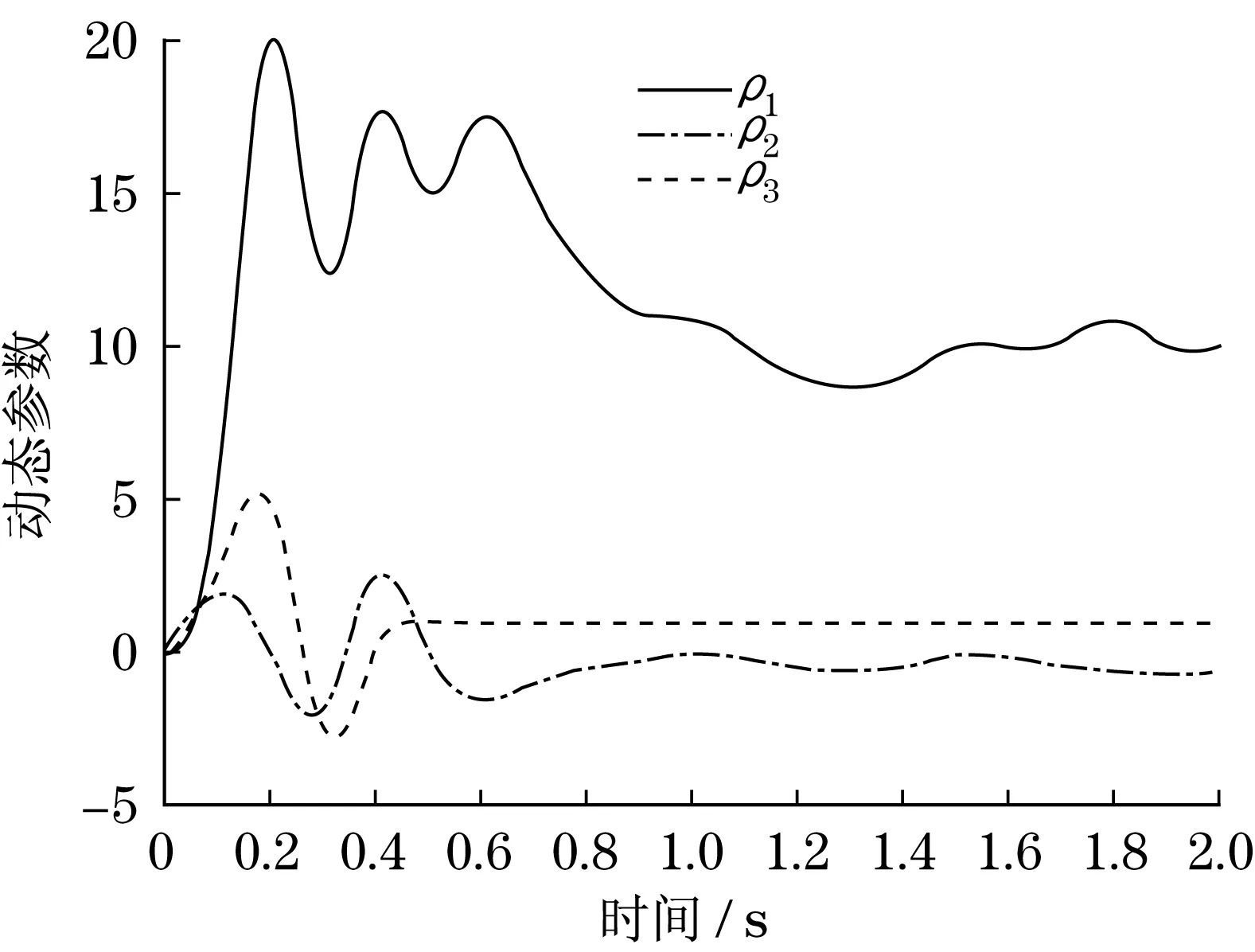
图5 系统识别的仿真结果Fig.5 Simulation results of system identification
4.2 简化模型控制效果仿真
得到简化模型动力参数之后,利用Matlab分别采用PD控制器及非线性同步控制器进行仿真验证.控制器跟踪控制的性能评价指标如下:① 关节位置误差的幅值;② 末端执行器位置误差的幅值.仿真结果显示:PD控制下关节1和2以及末端执行器的位置误差如图6所示,非线性同步控制下关节1和2以及末端执行器位置误差如图7所示.
由6可知:PD控制下关节1的位置误差幅度0.007 9 mm,关节2的位置误差幅度0.007 0 mm,末端执行器的位置误差X向幅度0.008 5 mm,Y向幅度0.009 3 mm.由图7可知:非线性同步控制器下关节1的位置误差幅度0.003 9 mm,关节2的位置误差幅度0.004 9 mm,末端执行器位置误差X向0.007 2 mm,Y向0.006 8 mm.说明由于采用了非线性饱和函数,在非线性控制器下关节1、关节2以及末端执行器的位置误差幅度均有明显减小,非线性同步控制器在两种性能评价指标上均优于PD控制器.结果表明,本文所提出的建模方法可以有效地消除闭环系统中的非线性模型效应.
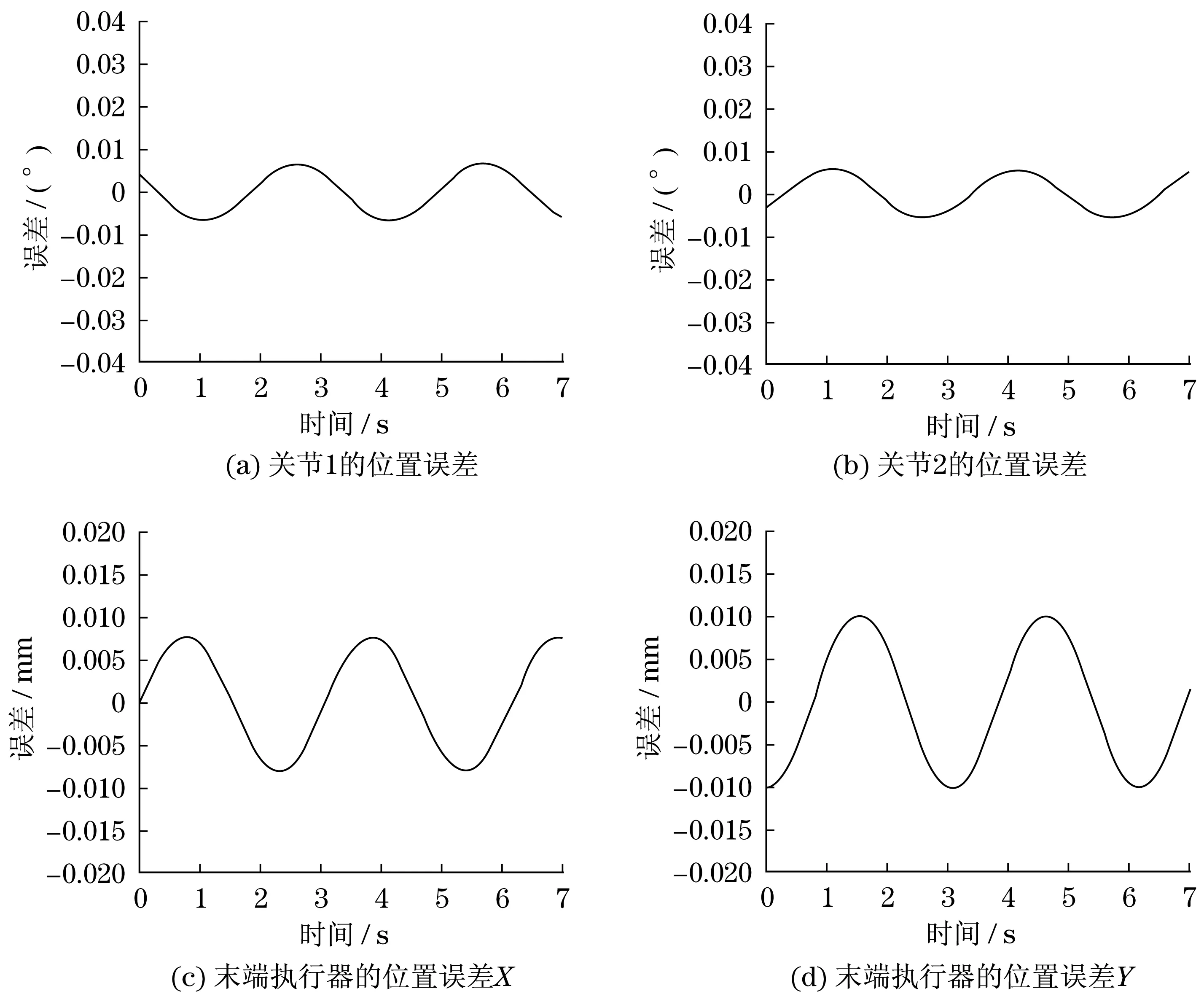
图6 PD控制下关节及末端执行器位置误差Fig.6 Position error of joint and end effector under PD control

图7 非线性同步控制下关节及末端执行器位置误差Fig.7 Position error of joint and end effector under nonlinear synchronous control
5 结语
本文建立了2自由度并联机器人腿简化模型,将机器人腿看作是一个2自由度机械手.对传统动力学方程进行改进,建立了简化模型的动力学方程.为了识别简化模型动态参数,建立参数识别算法.在ADMAS仿真软件中识别系统的动态参数,在Matlab中对两个关节及末端执行器位置进行仿真验证,比较PD控制器及非线性同步控制器跟踪控制性能.结果显示:采用非线性同步控制器不仅关节位置误差小,而且末端执行器的位置误差也降低,说明本文采用的建模思路对于多自由度并联机器人腿的分析具有借鉴意义.
