3自由度柔性并联机构自抗扰控制研究

周 微

(常州机电职业技术学院 机械工程学院,江苏 常州 213164)

柔性并联机构(Compliant Parallel Mechanism)是一种利用自身柔性杆件的弹性变形来传递运动的新型机构,通过有效地运用弹性变形来改善机构的运动特性,具有结构刚度强、无摩擦磨损、免装配润滑和运动精度高等优点,在生物医学、高精度机床和机器人等领域有着广泛的应用[1].由于柔性并联机构的控制系统具有复杂多变量、强非线性和高耦合的特点,如何提高柔性并联机构的轨迹跟踪精度是控制研究急需解决的问题[2].文献[3]从柔性并联机构非线性与线性间的不确定性方面进行分析,基于H2/H∞混合鲁棒控制,研究了机构的位置追踪状态.文献[4]以一种柔性并联机构为研究对象,采用合成法和PD相结合的控制方式,设计了一种基于机构动力学方程的新型控制器.文献[5]采用一种结合应变速度和最佳状态的反馈控制器,研究了平面3-RRR柔性并联机构的残余振动.文献[6]采用Hensens & Kostic理论来补偿柔性并联机构的Lagrange方程,从而补偿机构的单位定点误差,分析了机构分别在S型、T型速度规划算法下的位置和速度误差.为了改善柔性并联机构的位移轨迹跟踪精度,本文基于3-PRR柔性并联机构,设计了一种自抗扰控制器(Active Disturbance Rejection Control,ADRC),并分析了机构的位移追踪误差,有效提高了机构的控制稳定性.

1 3-PRR柔性并联机构模型

1.1 机构模型

本文以3-PRR柔性并联机构为研究对象,由于柔性并联机构是以传统的并联机构为设计原型,并运用拓扑优化方法得到的一种新型机构,拓扑优化方法并没有改变机构间的运动关系,故可以运用传统3-PRR并联机构的理论来分析3-PRR柔性并联机构[7].

3-PRR柔性并联机构有3个自由度,即沿XY方向的平移和绕Z方向的转动,模型如图1所示.机构由定平台、动平台以及连接动定平台的3条对称支链构成.机构的定平台A1A2A3和动平台C1C2C3均为等边三角形,每条运动支链由1个移动副(P副)和2个转动副(R副)构成.移动副连接着定平台的各个顶点和转动副,是机构的驱动副,驱动距离为di(i=1,2,3).连杆BiCi(i=1,2,3)长度均相等,两端为转动副且与动平台相连.在动平台的中心建立定坐标系O-xy,其中，θi为连杆BiCi与x轴正向的夹角,αi为AiBi与x轴正向的夹角,θP为动平台C1C2C3绕z轴的旋转角度.点P为动平台的几何中心,即机构的运动末端.

1.2 机构Jacobian分析

基于图1的机构模型,采用闭环矢量法对机构的3条支链进行求解,可以得到支链的运动学约束关系，即

(1)

将式(1)的矢量方程投影至x轴和y轴,可得

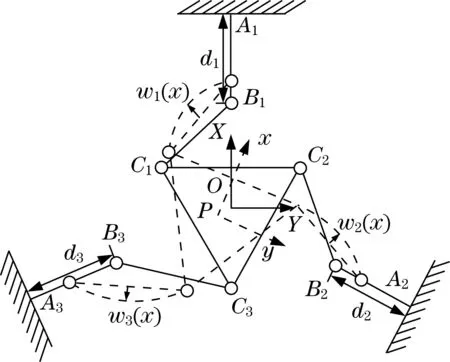
图1 3-PRR柔性并联机构模型Fig.1 Model of 3-PRR compliant parallel mechanism

(2)

式中:(xAi,yAi)为点Ai的坐标.

对式(2)求导,可得

(3)

2 系统控制器的设计

2.1 PID控制器的设计

PID控制是一种通过利用反馈误差的方式来达到控制效果的闭环控制,是运用最广泛的控制技术.PID控制器通过参数整定,调节比例、积分和微分3个参数值以形成控制器的理想输出,这些参数的线性组合可以反映控制系统的响应速度和稳定性能[8].PID控制器的原理如图2所示,其中，Integrator为积分器,Derivation为微分器.Kp,Ki,Kd3个参数的调节对于控制系统的效果有着关键作用,本文采用临界曲线法来对Kp,Ki,Kd进行参数整定,使其达到最佳的控制效果.

图2 PID控制原理图Fig.2 Schematic diagram of PID control

2.2 ADRC控制器的设计

ADRC主要由非线性跟踪微分器、扩张状态观测器和非线性状态误差反馈3部分组成,原理如图3所示.为了提高控制系统的动态特性,解决系统快速响应和超调间的矛盾,运用扩张状态观测器对被控对象进行实时在线估计,利用跟踪微分器安排过渡过程,并对系统的总扰动进行补偿.

图3 ADRC控制原理图Fig.3 Schematic diagram of ADRC control

2.2.1 跟踪微分器

跟踪微分器是自抗扰控制的前馈通路部分,主要作用是处理系统的输入信号r(k),并提取出输入信号r(k)的跟踪信号r1(k)和微分信号r2(k).跟踪微分器可以根据输入信号的大小和控制要求来安排过渡过程,解决快速响应和超调间的矛盾,使系统的输入信号具有快速性且无超调的双重特点.跟踪微分器的输出方程为

(4)

式中:h为系统采样时间;r(k)为输入信号.fst(x1,x2,δ,h0)为非线性函数,

(5)

式中:δ为速度因子,决定系统的跟踪速度;h0为滤波因子,对噪声进行滤波处理;sgn(·)为符号函数;d与α的值为

d=δh0

d0=h0d

y=x1+h0x2

(6)

(7)

2.2.2 扩张状态观测器

扩张状态观测器是自抗扰控制的反馈通路部分,主要作用是将系统未建模部分、内部参数摄动以及外界干扰等因素归为一个新的状态,为系统提供新的反馈输入信号z(k)、扩张状态变量和各阶状态变量.通过扩张状态变量估算系统的干扰,从而利用反馈来补偿系统扰动.扩张状态观测器的输出方程为

(8)

式中:y(k)为系统输出信号;u(k)为系统非线性状态反馈输出信号;ε0为初始输出误差信号;z1(k),z2(k),z3(k)分别为跟踪信号、微分信号和反馈误差信号;b0,β1,β2,β3为控制参数;fal(ε0,αi,δ0)为非线性函数,

(9)

式中:δ0为初始速度因子;ε为输出误差信号;αi为实数,0<αi<1.

2.2.3 非线性状态误差反馈

由于PID控制律的Kp,Ki,Kd线性组合往往会造成控制系统快速响应与超调之间的矛盾,因此，非线性状态误差反馈将Kp,Ki,Kd的线性组合转变为非线性组合,从而实现自抗扰控制.非线性状态误差反馈的控制律方程如下:

e1(k)=r1(t)-z1(k)

e2(k)=r2(t)-z2(k)

u0=kpfal(e1,α01,δ1)+kdfal(e2,α02,δ1)

(10)

式中:kP,kd为非线性状态反馈的比例和微分参数;e1(k),e2(k)分别为跟踪误差信号和微分误差信号;fal(e2,α02,δ1)与式(9)相同,0<α01<α02<1.

2.3 ADRC控制器稳定性分析

假设系统为不确定参数2阶系统,ei=xi-zi(i=1,2,3),那么可得到系统的偏差状态方程为

(11)

(12)

由式(12)可知,参数ω0决定了扩张观测器的控制性能,且偏差状态方程的3个极点都处于同一位置,此时有

(13)

由于fal(e1,a01,δ)为奇函数,当kp>0时,P(e1)>0.因此，控制器方程可简化为

(14)

系统的平衡点为e1=e2=0.

选取Lyapunov函数为

(15)

(16)

因此，控制系统处于半负定,符合Lyapunov稳定性的要求[9].

3 控制仿真

根据柔性并联机构的结构特性,不断调节控制器的参数,直至机构运动平稳且误差波动较小,仿真时间为10 s.PID控制器的控制参数Kp=8.5,Ki=0.5,Kd=0.2.ADRC控制器的参数为δ=6,α1=0.3,α2=0.1,β1=51,β2=372,β3=1 058,δ0=0.004,kp=18,kd=0.9,α01=0.6,α02=0.8,δ1=0.05.系统在X,Y,Z3个方向的PID控制和ADRC控制位移跟踪曲线分别如图4～图6所示.

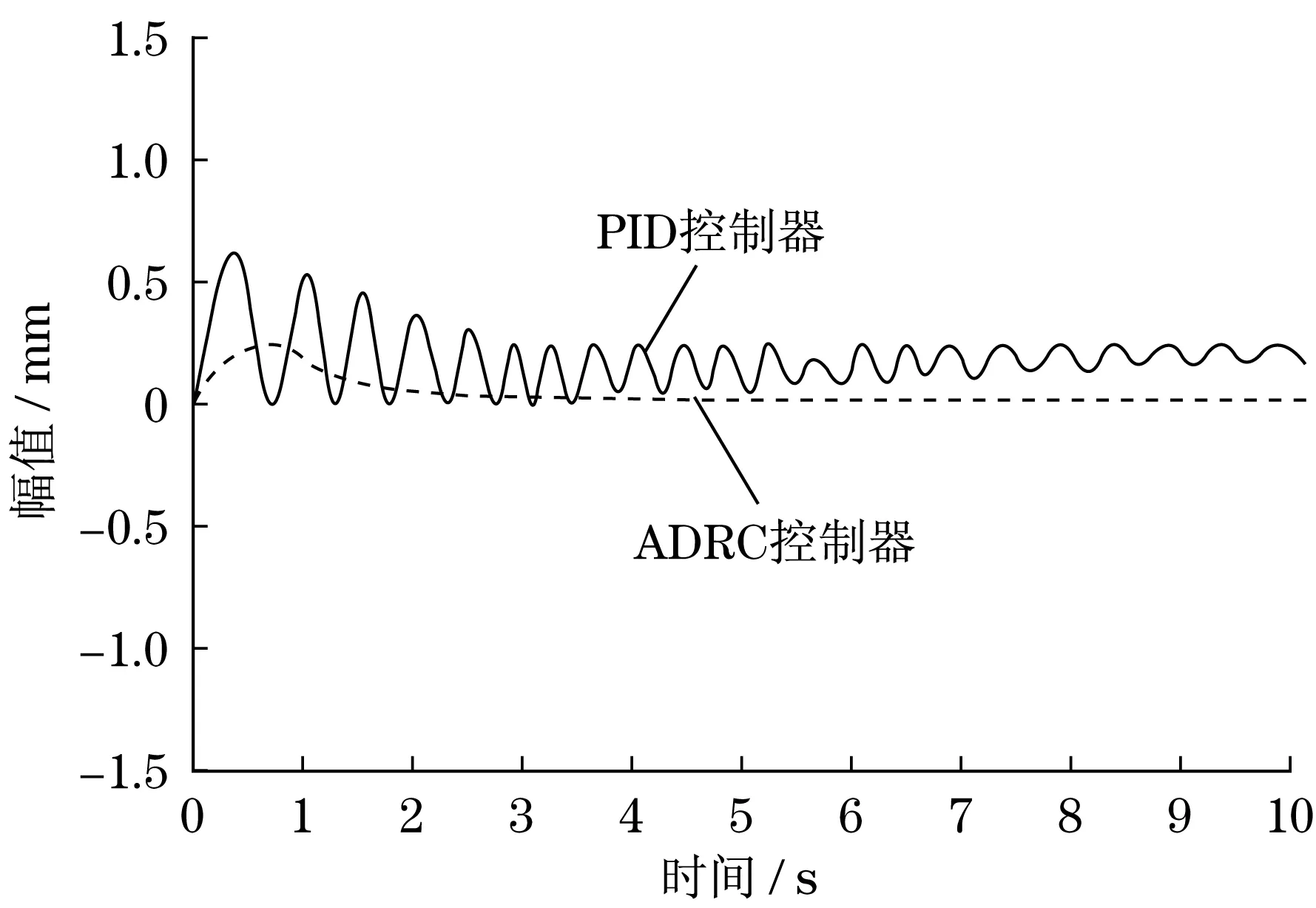
图4 X方向位移跟踪误差曲线Fig.4 Displacement tracking error curve of X-direction

图5 Y方向位移跟踪误差曲线Fig.5 Displacement tracking error curve of Y-direction

由图4～图6可知：PID控制和ADRC控制在最初的3 s时间内,均存在较大的轨迹跟踪误差,轨迹跟踪的稳定性较差.经过一段控制算法的实时运算,两种控制方式都能达到一定的控制精度,但是随着ADRC控制不断消除快速响应与超量间的矛盾,使得机构3个方向的轨迹跟踪误差逐渐趋近于零,而PID控制无法消除该矛盾,轨迹跟踪误差还是较大.由表1可知,与PID控制相比,ADRC控制的超调量和调整时间都更短,说明ADRC控制的稳定性更好,在响应速度方面更优.

图6 Z方向位移跟踪误差曲线Fig.6 Displacement tracking error curve of Z-direction

表1 仿真结果Tab.1 Simulation result

4 结语

基于3-PRR柔性并联机构模型,根据闭环矢量法分析了机构的运动学方程,得到的输入输出Jacobian矩阵为控制系统提供了参考输入.分别设计了PID控制器和ADRC控制器,并分析了ADRC控制器的非线性跟踪微分器、扩张状态观测器和非线性状态误差反馈部分.研究了柔性并联机构在PID控制和ADRC控制两种不同控制方式下的位移轨迹误差曲线,结果表明:ADRC控制可以解决快速响应与超调间的矛盾,轨迹跟踪误差小,响应速度快,可以满足柔性并联机构高追踪精度的要求.