基于偏最小二乘法的集装箱吞吐量预测模型研究

丁文涛，刘孟琦，齐 越，苏孟超，李宜军，房 卓

（1.交通运输部规划研究院，北京 100028；2.大连理工大学建设工程学部，辽宁 大连116023）

引言

集装箱运输是现代交通的重要发展方向，也是港口地位和功能的重要标志，科学准确地预测港口集装箱吞吐量，对于指导港口发展和建设具有重要的意义。目前港口集装箱吞吐量预测方法可以分为两大类，即定性预测方法和定量预测方法，常用的定性方法有Delphi法、专家调查法等，定量预测法有因果分析法、时间序列分析法、组合预测法等。如戴霖，黄浩[1]等建立马尔科夫模型预测港口吞吐量，刘明维[2]等利用指数平滑法进行吞吐量预测，刘长俭[3]等采用 BP人工神经网络构建港口集装箱吞吐量预测模型，朱小檬[4]等基于时间序列-因果分析法相结合的方法对海港集装箱吞吐量进行中长期预测，陈昌源[5]等利用改进的 GM(1,1)对上海港集装箱吞吐量进行预测。

综合来看，传统方法多基于少量解释变量，造成数据信息的流失，并且无法很好地解决解释变量间的共线性问题。另一方面，这些方法都需要足够多的历史数据来支撑，更适用于集装箱运输发展较为成熟的港口。我国有较多港口的集装箱运输尚处于起步发展阶段，传统的方法较难预测未来的吞吐量规模。偏最小二乘法（PLS）能够较好解决解释变量共线性及样本数量过少导致的无法有效建模的问题，因此本文采集影响港口集装箱吞吐量的众多影响因素并利用PLS方法建立预测模型。

1 偏最小二乘回归建模

1.1 建模思想

偏最小二乘法（PLS）是由瑞典统计学家Herman OA Wold和Svante Wold一起开发的线性回归模型，最初应用于社会科学领域，现在主要应用在化学计量学领域并广泛应用于其他领域。PLS方法将主成分分析与多元线性回归和典型相关分析结合到一起，将自变量和因变量投影到新空间提取主要成分，按照相关性程度排序确定提取成分个数后，建立线性回归模型。相比标准回归，PLS方法特别适用于自变量存在多重共线性和预测变量矩阵维度多于观测值的情况。

1.2 基本原理

设自变量为矩阵En×m，因变量为矩阵Fn×p。将矩阵进行数据标准化，每个样本减去一个维度变量均值然后除以该维度的标准差。自变量矩阵标准化后为E0(n×m)，因变量矩阵标准化后为F0(n×p)。

提取主成分t1：

提取主成分u1：

式中：w1为权重系数且为单位向量，；c1为权重系数且为单位向量，。

根据主成分原理和典型相关分析，t1与u1的方差达到最大且t1与u1的相关度达到最大值。故要求：

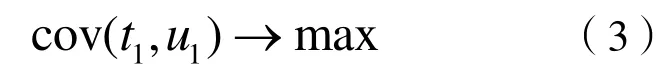
通过拉格朗日方法求解，w1为矩阵E0′F0F0′E0的最大特征值的特征向量，c1为矩阵F0′E0E0′F0的最大特征值的特征向量，并且均单位化。解出w1，c1即可求出t1与u1。

从而建立E0，F0对t1与u1的回归方程：式

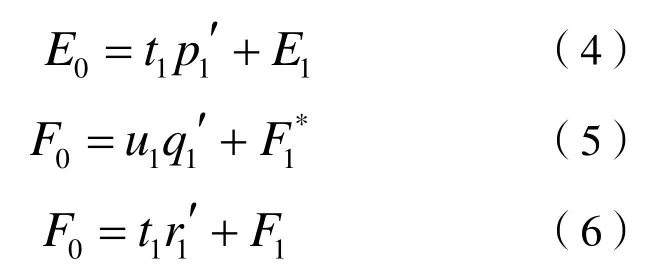
中：E1,F1*,F1是三个回归方程的残差矩阵。

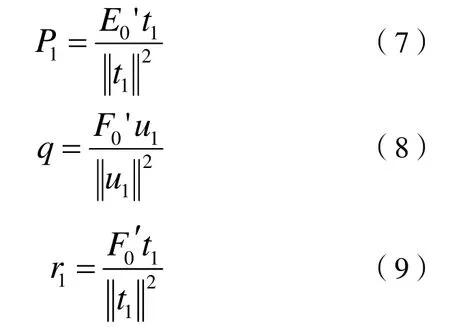
用E1和F1取代E0和F0，按照上述过程，求出第二个轴w2和c2以及t2和u2，并重新建立E1和F1与t2和u2的回归方程，直到求出所有主成分。（何时终止提取成分，后文详述）

若E0的秩为A，则可以得到：

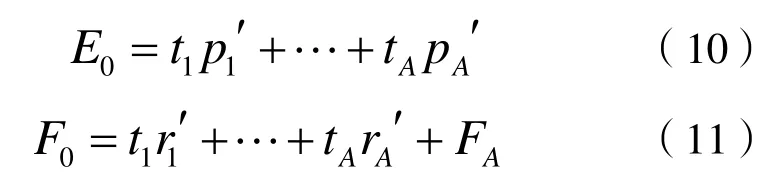
由于t1,…tA都是E01…E0m的线性组合,m=1,2,…，带入上式中，可得到：

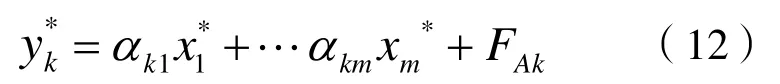
式中：k=1,2,…，且FAk为残差矩阵FA的第k列。

确定提取主成分的个数th：

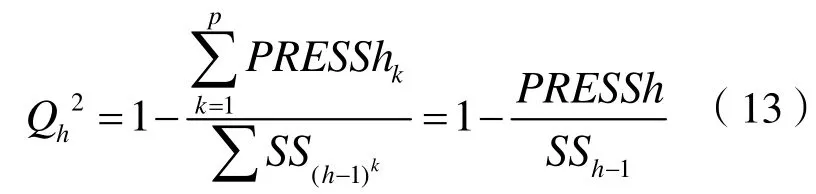
当Qh2≥(1-0.952)=0.0975时，th成分边际贡献显著，可以确定h，然后将其转化为y与x1,x2,…xh的回归方程[6]。

1.3 变量投影重要性分析

每一个自变量在解释因变量作用的重要性程度可以用变量投影重要性（VIP）来分析，具体的计算公式为：

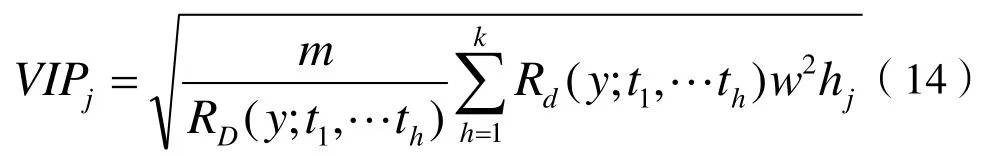
式中：VIPj是第j个变量xj的投影重要性指标；m为自变量个数；whj是wh的第j个分量；RD(y,th)是th对y解释的变异精度；是t1…th对y的累计解释能力。

2 算例分析

为了验证偏最小二乘回归模型的有效性和准确性，本文拟采用黄骅港进行验证。黄骅港于2012年开始运营集装箱业务，实现了年均40 %以上的快速增长，2018年完成集装箱吞吐量72万TEU。新

时期，“一带一路”、京津冀协同发展、设立雄安新区等重大战略陆续实施，黄骅港的发展环境发生了较大的变化，科学把握未来集装箱吞吐量是十分必要和有意义的。

2.1 数据选取

集装箱吞吐量与港口腹地的经济发展和基础设施的规模密切相关，根据对黄骅港集装箱装箱货物及货源地的调查，选取影响黄骅港集装箱吞吐量的相关因素如下：沧州市生产总值（x1，亿元），沧州市全社会固定资产投资值（x2，亿元），沧州市消费品零售值（x3，亿元），沧州市外贸进出口值（x4，亿美元），沧州市出口值（x5，亿美元），沧州市公路里程（x6，万km），沧州市海铁联运量（x7，t），河北省生产总值（x8，亿元），河北省粮食产量（x9，万t），河北省第二产业总值（x10，亿元），河北省第三产业总值（x11，亿元），河北省进出口总值（x12，亿美元），河北省铁路运营里程（x13，km）以及黄骅港集装箱吞吐量（y，TEU），具体数据见表1。

表1 黄骅港集装箱吞吐量影响数据采集

2.2 多重共线性诊断

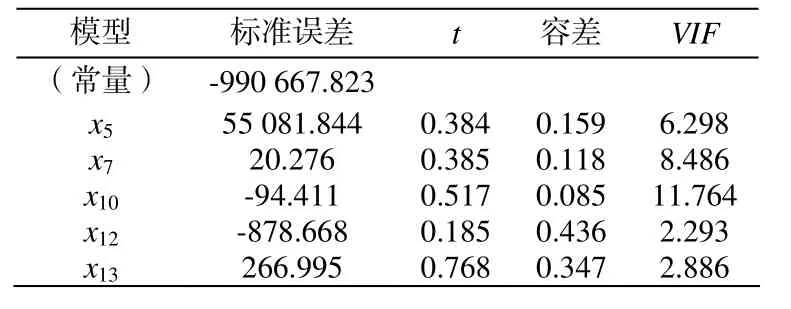
表2 回归系数

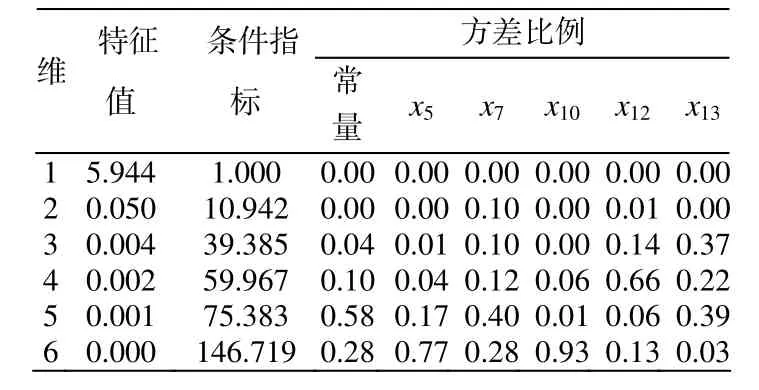
表3 多重共线性诊断

黄骅港 2012年才开始发展集装箱业务，样本数量小于变量数量，且经过SPSS初步计算，相关系数大于0.96，有严重多重共线性问题，采用普通的回归方法无法建立回归方程，一般的方法是采用逐步回归方法建立多元回归方程。

经过SPSS软件计算，得出的多元回归方程的回归系数以及多重共线性诊断如表2和表3所示。

从表2中可看出，经过逐步回归后的变量VIF值依旧偏大，其中x10的VIF值大于10，从表3中可以看出最小特征值为 0，其中最大方差比例达到0.93，接近于 1，可以看出逐步回归后建立的多元回归方程多重共线性依旧很严重，本文采用PLS方法解决共线性问题建立预测模式。

2.3 集装箱吞吐量偏最小二乘法回归方程确定

利用 SPSS软件中的 PLS算法，选取2012—2016年影响黄骅港集装箱吞吐量的13个因素进行偏最小二乘法，将 2017年数据用于检验方程，最终经过计算选出4个主成分（h=4），计算结果如表4所示。

可以看出，前4个主成分可完全解释自变量和因变量的信息，即选取4个主成分可准确地提取信息。

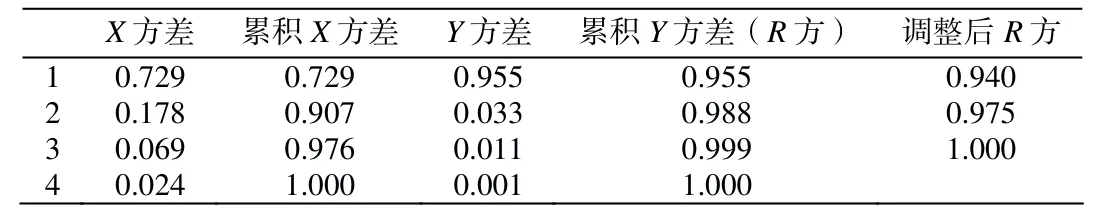
表4 已解释的方差比例

通过软件计算结果可以得到标准化偏最小二乘回归方程：

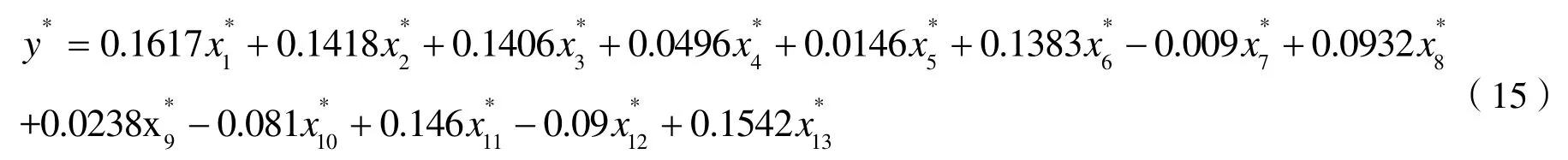
将标准化偏最小二乘回归方程中的标准化因变量还原成普通变量，得到黄骅港集装箱吞吐量与各自变量的回归方程：

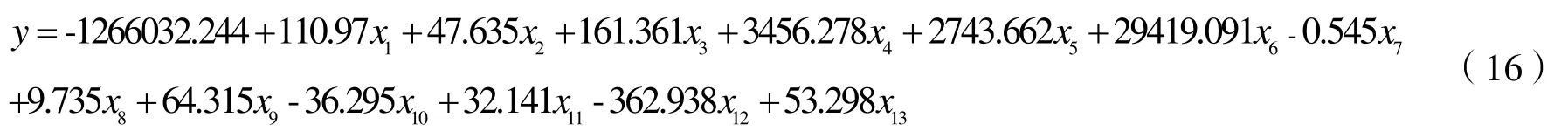
2.4 拟合效果和预测效果分析

将 2012—2016年各自变量数据带入预测模型中得到拟合值（见表5），与实际值相比较并算出两者的残差值（见表5和图1）。将 2017年各自变量数据带入预测模型中得到 2017年吞吐量预测值并与实际值比较检验模型预测精度（见表6）。

表5 黄骅港集装箱吞吐量实际值与预测值比较

表6 黄骅港集装箱吞吐量2017年预测结果

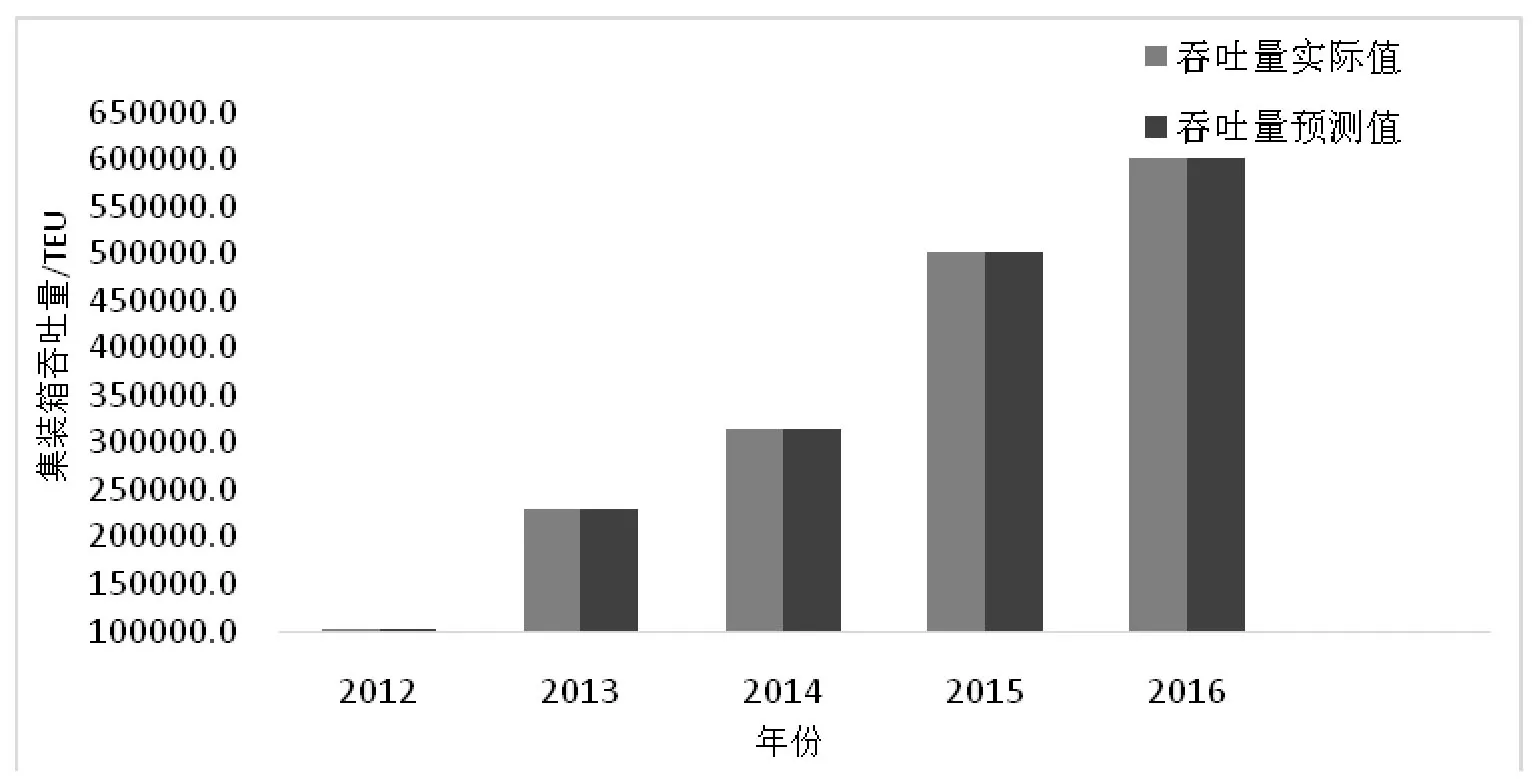
图1 黄骅港2012—2016年集装箱吞吐量实际值与预测值比较

从图1中看出，黄骅港集装箱吞吐量实际值与拟合值拟合效果良好，从表5中看出拟合值与实际值残差值都在1 %以内，可以见得偏最小二乘法能够有效的消除多重共线性，得到精确度较高的回归模型。从表6中可以看出，采用偏最小二乘回归模型预测误差在5 %以内，预测精度较高。

2.5 变量投影重要性指标（VIP）

计算出影响黄骅港集装箱吞吐量变量重要性指标并绘制直方图（见图2），从图中可以看出，沧州市生产总值、沧州市社会固定资产投资值、沧州市消费品零售值、沧州市公路里程数、沧州市海铁联运量、河北省生产总值、河北省农业产量、河北省第三产业总值、河北省铁路运营里程这9个因素的投影重要性指标大于1，说明这9个指标是影响黄骅港集装箱吞吐量的重要因素。

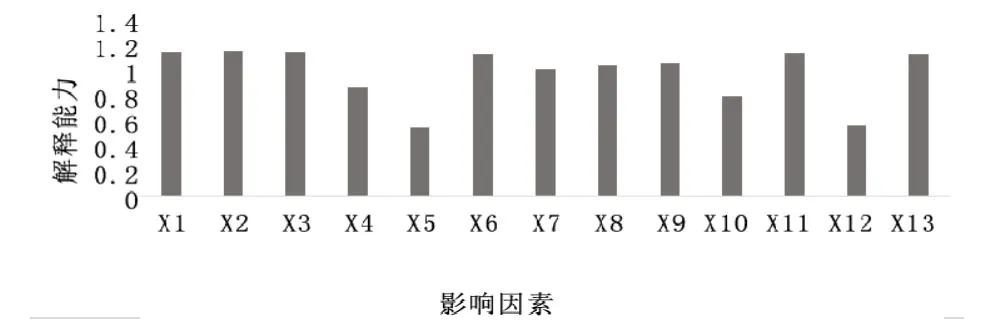
图2 变量投影重要性指标

2.6 回归结果解释

从得到的回归方程中可以看出沧州市生产总值、沧州市社会固定资产投资值、沧州市消费品零售值、沧州市外贸进出口值、沧州市出口值、沧州市公路里程、河北省生产总值、河北省农业产量、河北省第三产业总值、河北省铁路运营里程对集装箱吞吐量起促进作用，而河北第二产业总值和河北进出口值对黄骅港集装箱吞吐量起负向作用。

黄骅港正在大力发展煤炭、粮食运输的“散改集”，这占现有集装箱吞吐量的70 %，而目前工业适箱货运量还没有得到充分释放，腹地工业产生的集装箱多由天津港运输，所以河北省第二产业总值对黄骅集装箱吞吐量影响有限。随着沧州渤海新区的发展，临港工业所产生的适箱货运量将会逐步增加，这在以后的建模中要加入进去。黄骅港腹地冀中南地区外贸集装箱主要经天津港出口，所以河北省外贸进出口额对黄骅港集装箱吞吐量影响很小。随着津冀港口公司参与到黄骅集装箱码头运营，以及中韩自贸协定的推动，黄骅港承担内支线运输将逐步增加，近洋直航也将在未来开辟，这也要在以后的建模中考虑。

2.7 黄骅港集装箱吞吐量中长期预测

将影响吞吐量因素的指标按照灰色模型法GM(1,1)进行预测，并且将预测的影响因素值带入建好的偏最小回归二乘模型，预测2020年和2025年的黄骅港集装箱吞吐量，结果见表7。

表7 2020年和2025年黄骅港集装箱吞吐量预测结果

3 结语

通过 PLS方法能够提取变量中解释性强的成分，去除变量中多重相关信息，保留变量原有信息，该法能够最大限度的利用影响港口集装箱吞吐量的众多变量信息。黄骅港集装箱吞吐量预测算例表明，该方法能够在历史年份数据较少的情况下，精确度较高的预测集装箱吞吐量，算例中给出的黄骅港集装箱吞吐量2020年、2025年预测结果，也可为黄骅港发展建设预测提供参考。