基于粗糙集和加权TOPSIS法的弹目匹配模型

李亚雄，徐 萌，张斌伟

(1 火箭军工程大学，西安 710025； 2. 31102部队，南京 210016)



【装备理论与装备技术】

基于粗糙集和加权TOPSIS法的弹目匹配模型

李亚雄1，徐 萌2，张斌伟1

(1 火箭军工程大学，西安 710025； 2. 31102部队，南京 210016)

提出了基于粗糙集和加权TOPSIS法的弹目匹配模型；该模型充分考虑目标特性和战斗部毁伤效应匹配度，适应了弹目匹配固有的客观性和非线性跳跃变化特点；算例分析表明：该模型能够对各类武器打击各目标的优先顺序进行量化评估，解决了混合火力打击下打击目标的弹型选择问题。

粗糙集;TOPSIS法;弹目匹配

在使用多种武器对目标进行混合火力打击时，经常面临弹种选取顺序的问题，即有多种类型的武器都可以打击某一个目标，应当确定弹种的选取顺序。研究混合火力打击弹目匹配问题需要考虑的因素很多，比如作战目的复杂性、武器装备的成本、作战过程的协同性等等[1]，本文从典型常规导弹战斗部的毁伤效应与目标易损性的匹配程度入手研究混合火力打击弹目匹配问题，以匹配性为依据确定弹种选取顺序。

1 混合火力弹目匹配性评价指标体系及求解思路

1.1 弹目匹配性评价指标体系

典型常规战斗部的毁伤效应主要包括破片杀伤效应、弹头侵彻效应、冲击波爆破效应、侵彻爆破效应和延时爆破效应等5种效应。根据目标易损性分析，与此相应的目标抗毁效应主要包括抗破片杀伤效应、抗弹头侵彻效应、抗冲击波爆破效应、抗侵彻爆破效应和抗延时爆破效应。对于同一效应，典型战斗部毁伤效应与目标抗毁效应的指标和量纲是一致的，例如，冲击波爆破效应和抗冲击波爆破效应都是用冲击波超压来量化。选取以上5种毁伤效应的匹配度作为弹目匹配的5个指标，记为c1、…、c5，综合考虑常规导弹战斗部与目标在5个指标下的匹配情况，得到弹目匹配顺序。弹目匹配性评价指标体系如图1所示。

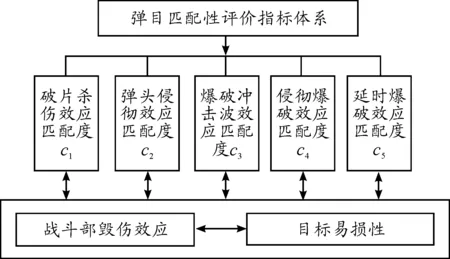
图1 弹目匹配性评价指标体系

采用hijk表示第i种战斗部与第j种目标在第k种毁伤效应下达到既定毁伤程度的匹配度，Wik为第i种战斗部的第k种毁伤效应能够达到的最大值，Vjk为第j种目标在第k种抗毁效应下达到既定毁伤程度能够抵抗的最大值。

hijk具有以下性质：

1) 当战斗部i不存在第k种毁伤效应时，Wik=0，对任一目标j，有hijk=0。

2) 当hijk=1，表示弹目达到最佳匹配，hijkl>1，表示战斗部威力比毁伤目标需要的威力要大；hijk<1，表示战斗部威力无法达到预期的毁伤程度。hijk为中介指标，其值过大或者过小表示不适宜匹配。

3) hijk随具体的弹型和目标的不同而具有非线性跳跃变化特性，例如战斗部i与目标j的破片杀伤效应匹配度很好，但是延时爆破效应匹配度却为0。

1.2 弹目匹配性评价求解思路

基于混合火力打击弹目评价指标的以上特点，采用粗糙集属性重要性原理[2-3]确定指标权重，将权重加入TOPSIS法[4-16]，求出最优解和最劣解，并得到各弹型与目标的匹配情况到最优解的加权欧氏距离和贴近度，由贴近度确定弹目匹配顺序。

弹目匹配指标体系确定后，下一个需要解决的问题就是确定指标间的权重。目前，指标权重确定的方法有很多，如层次分析法、德尔菲法、模糊评定法等。混合火力弹目匹配评价指标具有以下特点：特定弹型的毁伤效应往往主要体现在某一种或极少数的几种；对某个目标打击，造成有效毁伤的效应同样也是少数，不可能包含所有的毁伤效应。因此，在确定评价指标权重时，需要考虑指标客观性，而粗糙集理论具备的重要度原理能够较好地满足以上需求。

2 基于粗糙集理论的弹目匹配指标权重计算方法

2.1 粗糙集的基本概念

粗糙集理论是由波兰数学家Z.Pawlak于1982年提出的，目前已广泛应用于解决不确定、不精确和不完全数据的多属性决策问题。其中主要的基本概念定义如下：

1) 决策信息系统。信息系统是粗糙集理论研究的主要对象，通常用四元组S=(U,A,V,F)来表示，其中，U为对象集，U={x1,x2,…,xn}，xi(i≤n)称为一个对象；A为属性集，A={a1,a2,…,am}，aj(j≤m)称为一个属性；V为属性的值域；F={fj|j≤m}，fj为每个对象的每个属性赋予信息值，称为信息函数。假如A=C∪D且C∩D=φ，即A包含条件属性集合C和决策属性集D，则S称为信息系统。

2) 等价关系。对属性子集R⊆A，等价关系ind(R)为

3) 依赖度。依赖度k，即Q以程度k依赖于P，其中

4) 属性子集的重要性。sig(C′)为属性子集C′∈C关于D的重要性，其中

5) 指标的重要性、权重。指标ck∈C在指标集C中的重要性由C中去掉ck之后引起的信息量变化大小来表示，即

指标ck的权重ωk为

2.2 基于粗糙集理论的弹目匹配指标权重计算步骤

步骤1：获取原始数据矩阵，构建决策信息系统。对于弹目匹配问题，对象集U={x1,x2,…,xn}为可选的弹型集合；条件属性集C={c1,c2,…,ck}为5种毁伤效应的匹配度指标；决策属性集D={d}为弹目综合匹配度；匹配度hijk为原始数据信息矩阵。粗糙集理论，要求指标数据离散，按照模糊聚类分析的一般方法确定hijk对应的匹配等级。

步骤2：计算指标ck的posC-{ck}(D)。

步骤3：计算指标ck关于D的重要性sig(ck)。

步骤4：归一化ck的重要性，得到ck的权重ωk。

3 基于加权TOPSIS法的弹目匹配顺序确定方法

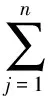
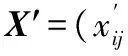
步骤2：建立规范化决策矩阵Y=(yij)m×n。

步骤3：构造加权规范化决策矩阵Z=(zij)m×n。

步骤4：计算各指标的最优解A+和最劣解A-。

4 仿真算例及结果分析

4.1 问题背景

假设现有A型侵彻子母弹、B型侵彻子母弹等11种弹型打击机场跑道目标，需要确定这11种弹型与目标间的弹目匹配优先顺序。

4.2 构造弹目匹配问题的决策信息系统

对象集U={x1,x2,…,xm}由这11种弹型组成；条件属性集C={c1,c2,…,cn}为5种毁伤效应的匹配度；决策属性集D={d}为弹目综合匹配度；匹配度hijk为原始数据信息矩阵，如表1所示。

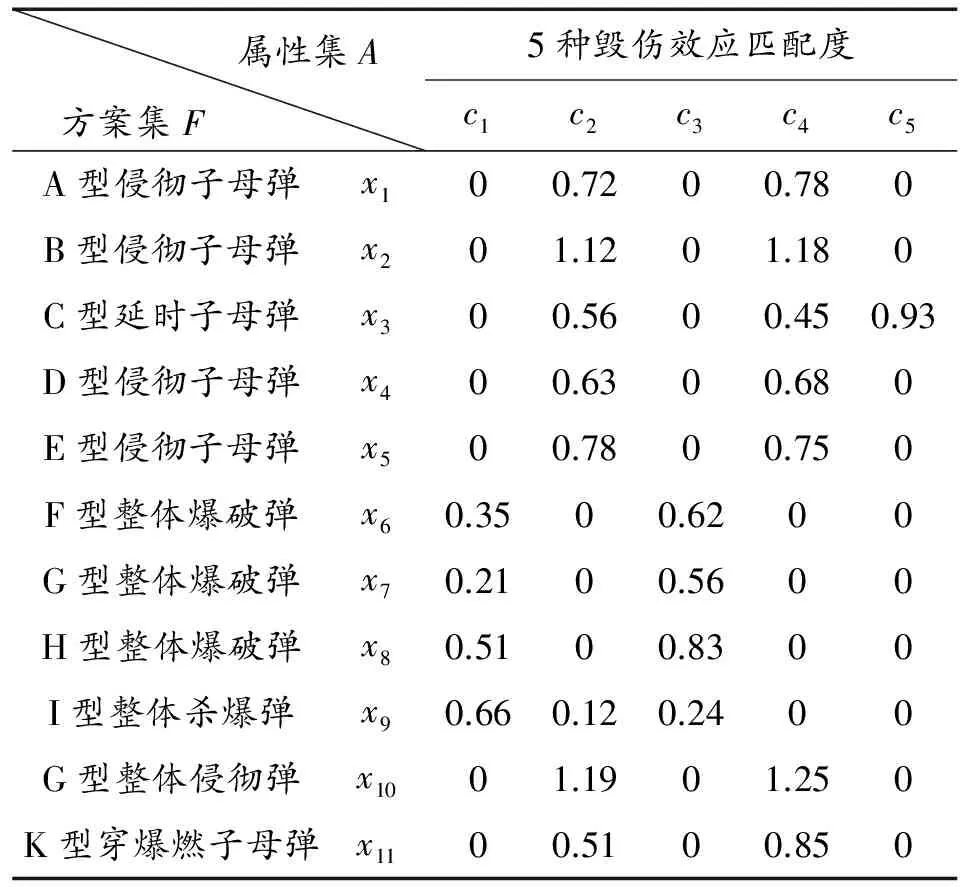
表1 弹目匹配原始数据信息矩阵

粗糙集理论要求指标数据离散，按照模糊聚类中的1～5标度法确定hijk对应的匹配等级。当hijk∈[0.8,1.2]时，认为“匹配度很好”，用标度5表示；当hijk∈[0.6,0.8)∪(1.2,1.4]时，认为“匹配度好”，用标度4表示；hijk∈[0.4,0.6)∪(1.4,1.6]时，认为“匹配度较好”，用标度3表示；hijk∈[0.2,0.4)∪(1.6,1.8]时，认为“匹配度一般”，用标度2表示；hijk∈[0.0,0.2)∪(1.8,+∞)时，认为“匹配度差”，用标度1表示。直接给出数据离散化后的匹配信息矩阵，如表2所示。

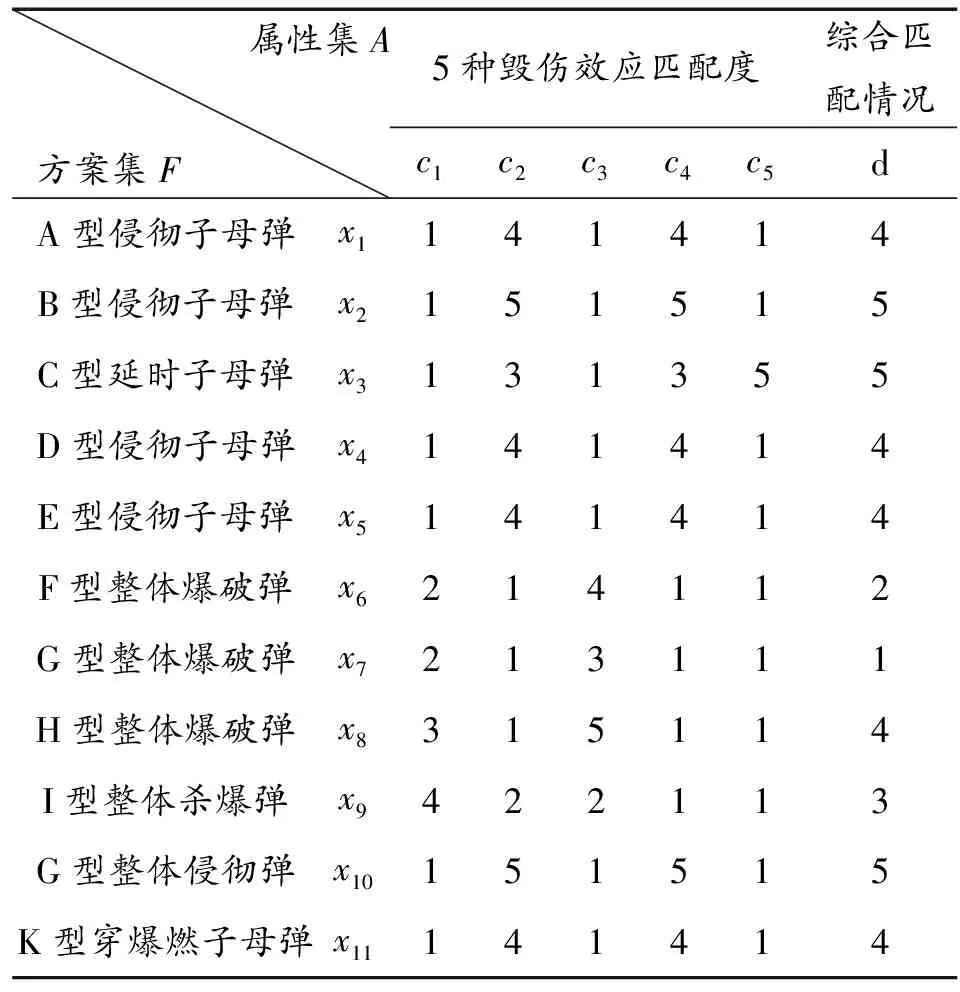
表2 弹目匹配信息矩阵

4.3 单个评价指标权重的计算

根据对象集划分规则，有：

U/C={(x1),(x2),(x3),(x4),(x5),(x6),(x7),(x8),(x9),(x10)}

U/D={(x2,x3,x10),(x1,x4,x5,x8,x11),(x9),(x6),(x7)}

PosC(D)={x1,x2,x3,x4,x5,x6,x7,x8,x9,x10}

γC(D)=|PosC(D)|/|U|=11/11=1

对指标ck，计算PosC-{ck}：

PosC-{c1}(D)={x1,x4,x5,x11}s

PosC-{c2}(D)={x1,x4,x5,x11,x2,x10}

PosC-{c3}(D)={x1,x4,x5,x11,x2,x10,x6,x7}

PosC-{c4}(D)={x1,x4,x5,x11,x2,x10}

PosC-{c5}(D)={x1,x4,x5,x11,x2,x10}

计算指标ck关于D的重要性sig(ck)：

sig(c1)=γC(D)-γC-{c1}(D)=1-4/11=7/11

sig(c2)=γC(D)-γC-{c2}(D)=1-6/11=5/11

sig(c3)=γC(D)-γC-{c3}(D)=1-8/11=3/11

sig(c4)=γC(D)-γC-{c4}(D)=1-6/11=5/11

sig(c5)=γC(D)-γC-{c5}(D)=1-6/11=5/11

对ck的重要性进行规一化，得到权重ωk：

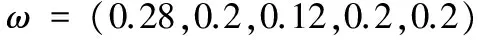
4.4 运用加权TOPSIS法确定弹目优先匹配顺序

单个评价指标的权值计算得到后，按照计算步骤，得到弹目匹配的优先次序如表3。

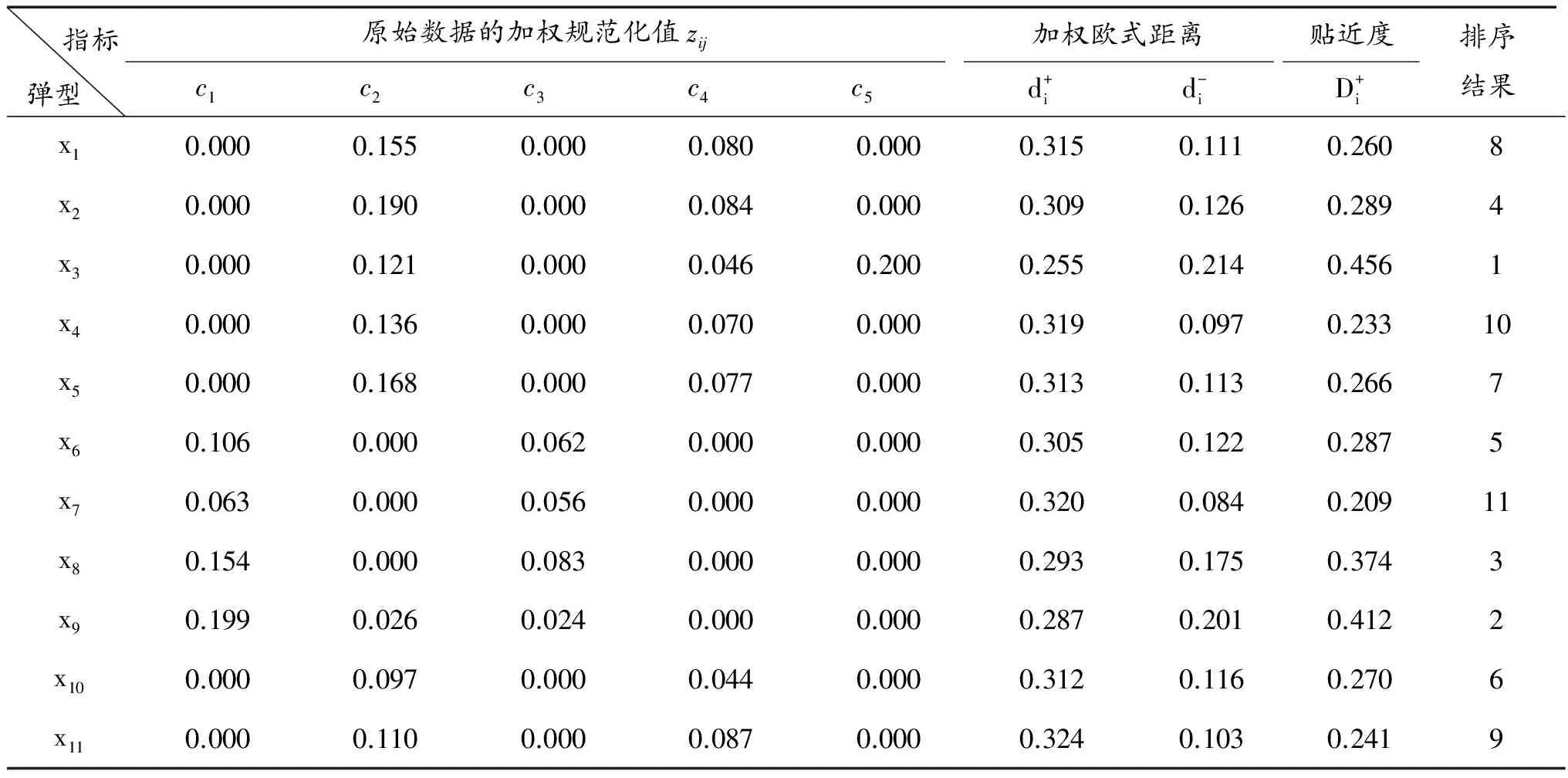
表3 基于加权TOPSIS法弹目匹配计算结果

如表3所示，11种弹型打击机场跑道目标的弹目匹配优先顺序为

5 结束语

本文分基于混合火力打击弹目匹配问题的特点，通过目标特性和典型常规导弹战斗部的毁伤效应分析，运用粗糙集理论和TOPSIS法建立了弹目匹配顺序求解模型，能够对各类武器打击各目标的优先顺序进行量化评估，解决了混合火力打击下打击目标的弹型选择问题。

[1] 沈寿林，朱江，王三喜.联合作战目标武器弹药匹配模型[J].指挥控制与仿真，2013，35(5)：47-50.

[2] 李远远.基于粗糙集的指标体系构建及综合评价方法研究[D].武汉:武汉理工大学，2009.

[3] 谭宗凤，徐章艳，王帅.一种改进的粗糙集权重方法[J].诗算帆工程与应用，2012，48(18)：115-118.

[4] 周亚.多属性决策中的TOPSIS法研究[D].武汉：武汉理工大学，2009.

[5] YAGER R，FILEV D P.Induced Ordered Weight Averaging Operators[J].IEEE Trans on Systems，Man，and Cybernetics，1999，29(2)：141-150.

[6] ZARAS K.Rough Approximation of A Preference Relation by a Multi-Attribute Stochastic Dominance for Determinist and Stochastic Evaluation Problems[J].European Journal of Operational Research，2001，130(2)：305-314.

[7] ROY A，PAL S K.Fuzzy Discretization of Feature Space for a Rough Set Classier[J].Pattern Recognition Letters，2003，24(6)：895-902.

[8] 郭美芳，柏席峰，刘晓燕.地下目标毁伤与防护技术发展研究[R].中国兵器工业集团第二一〇研究所，2008.

[9] 刘雅琼.多重毁伤效应综合评价方法研究[D].南京：南京理工大学，2009.

[10]庞伟宾.抗常规钻地武器坑道毁伤效应及安全防护层厚度研究[D].合肥：中国科学技术大学，2007.

[11]HAMBLING D.Novel Warhead May Bust the Deepest Bunkers[J].New Scientist,2005(7)：45-49.

[12]KLEPACZKO J R，BRARA A.An Experimental Method for Dynamic Tensile Testing of Concrete by Spalling[J].Internationel Journal of Impact Engineering 2001(25)：387-409.

(责任编辑 周江川)

Model of Missile Target Matching Based on Rough Setand Weighted TOPSIS

LI Ya-xiong1, XU Meng2, ZHANG Bing-wei1

(1.Rocket Force University of Engineering, Xi’an 710025,China;2.The No. 31102ndTroop of PLA, Nanjing 210016, China)

A matching model based on rough set and weighted TOPSIS was proposed. The model took the matching degree of the target characteristics and warhead damage effects into account and adapted to the inherent objectivity and nonlinear jump characteristics. The example analysis shows that the model can be used to quantify and evaluate the priority order of all kinds of targets, and solve the problem of the missile target selection under the mixed fire attack.

rough set; TOPSIS method; bullet matching

2016-09-21；

2016-11-25 作者简介：李亚雄(1979—)，男，博士，副教授，主要从事军事运筹学研究。

10.11809/scbgxb2017.04.003

李亚雄，徐萌，张斌伟.基于粗糙集和加权TOPSIS法的弹目匹配模型[J].兵器装备工程学报，2017(4):14-17.

format:LI Ya-xiong, XU Meng, ZHANG Bing-wei.Model of Missile Target Matching Based on Rough Set and Weighted TOPSIS[J].Journal of Ordnance Equipment Engineering,2017(4):14-17.

TJ765

A

2096-2304(2017)04-0014-04