多导弹协同作战制导律研究

王晓芳，郑艺裕，林 海

（北京理工大学 宇航学院，北京100081）

近程防御武器系统（CIWS）是一种配属在海军舰船上的装备，用来侦测与摧毁逼近的反舰导弹或相关的威胁飞行器，具有强大的威力［1］。为了有效地突破CIWS的拦截，反舰导弹通常采用饱和攻击战术［2］。饱和攻击一般要求导弹群同时到达目标区域并最终几乎同时命中目标。如果不能很好地实现2个“同时”，那么导弹突破敌方CIWS的难度将上升，饱和攻击将失去原有的意义。因此，如何充分共享战场实时信息，设计具有弹目距离协同（满足导弹群同时到达目标区域的要求）和攻击时间协同（满足同时命中目标的要求）功能的制导律，完成高效的、信息化的饱和攻击，是一个值得深入研究的课题。

目前，对具有攻击时间协同的制导律，学者们进行了一些研究［3－6］。文献［3］基于线性化后的弹目相对运动模型，采用最优控制理论得到一种可用于反舰导弹饱和攻击的攻击时间控制导引律。文献［4］将攻击时间作为协调变量，提出一种基于协调变量的时间协同制导律。文献［5］针对目标机动的情况，运用卡尔曼滤波理论估计目标加速度，确定了附加的目标指令，得到一种最优弹着时间可控制导律。但这些方法都假设导弹的速度为常数，而且需要估计导弹的剩余飞行时间。而在导弹实际飞行过程中，其飞行速度一般不会是一个固定不变的值［6］，剩余飞行时间的估计精度也难以保证。此时，上述制导律将不再适用或其精度将会大大降低。而对于弹目距离协同制导律的研究，目前还未见到相关的文献。

本文考虑导弹速度可变且避开对剩余飞行时间的预测问题，提出一种可实现多导弹弹目距离协同和攻击时间协同、从而对目标实现有效饱和攻击的协同制导律。首先，设定了各导弹期望的弹目距离；然后，基于经典比例导引律，采用时标分离原理、动态逆系统理论和线性系统理论设计了使每枚导弹的弹目距离趋于期望的弹目距离的弹目距离协同制导律。当各导弹距目标比较近时，为了能够精确攻击目标，又采用有限时间控制理论设计了视线角速度收敛制导律，使各导弹在接近目标的过程中视线角速度迅速收敛于零，最终几乎同时命中目标，也实现了攻击时间的协同。上述两部分制导律组成了具有弹目距离协同和攻击时间协同功能的协同制导律，仿真结果验证了其正确性和有效性。

1 比例导引律下的弹目相对运动模型

建立弹目相对运动模型时，不失一般性，考虑一枚反舰导弹攻击一个海上目标的情形，此时，导弹与目标的相对运动关系如图1所示。

图1中，Oxy为惯性坐标系；M，T分别代表导弹和目标；相应地，MT为弹目线，r为弹目距离，q为视线角；v为导弹的速度；φ，η分别为导弹的航向角和速度前置角（图示方向为正）；aτ，an分别为导弹的切向和法向加速度；vt，φt，ηt分别为目标的速度、航向角和速度前置角。

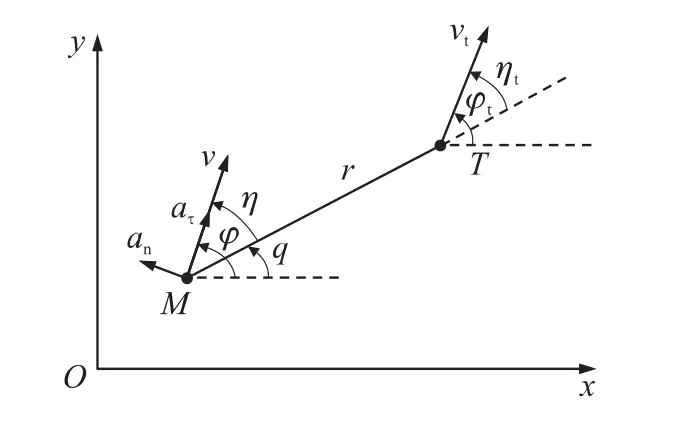
图1 导弹与目标的相对运动

经典比例导引律为

式中：K为比例系数。由图1可知：

由式（1）～式（3）可得：

为分析问题方便，假设目标静止，然后对式（5）求导，可得：

将式（4）代入式（6）得到的表达式，再将其代入式（7），另外，考虑在导弹飞行过程中通常速度前置角η不大，因此可认为cosη≈1，sinη≈η，则化简后的式（7）为

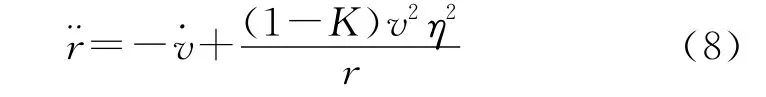
由式（8）可见，在相同速度变化率的基础上，比例系数K的取值对弹目距离的二阶导数有直接影响，从而会影响导弹与目标的接近速度和弹目距离r。因此，可通过控制K的取值实现对弹目距离的控制。

2 协同制导律设计

本文协同制导律由两部分组成：各导弹发射后按照弹目距离协同制导律飞行，使导弹群同步接近目标；当弹目距离小到一定程度时，为了确保有效地打击目标，转为使视线角速度收敛的制导律。由于各导弹的速度差别不会太大，而切换制导律时的弹目距离也比较小，因此，能够实现多枚导弹几乎同时命中目标。

2.1 弹目距离协同制导律

图2所示为n枚导弹协同攻击目标的情况，Mi表示第i枚导弹，T为目标，ri为第i枚导弹的弹目距离为期望弹目距离。

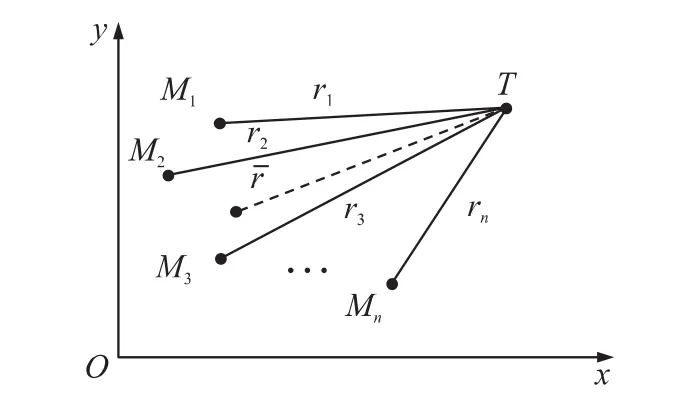
图2 多导弹协同攻击目标示意图

弹目距离协同制导律是使多枚导弹的弹目距离等于期望弹目距离、多枚导弹同步接近目标的制导律。因此，首先需确定期望弹目距离

2.1.1 期望弹目距离的确定及收敛性证明在设定期望弹目距离时，考虑以下2个因素：①应根据各枚导弹当前的弹目距离ri来设定

②为保证导弹逐渐接近目标以及最终能命中目标，须随时间变化收敛于零。

在深入分析上述2个因素的基础上，将期望弹目距离设定为所有参与协同作战导弹的弹目距离的平均值，即

接下来，对的收敛性进行证明。

取李雅普诺夫函数

显然，L为正定函数。对式（10）求导可得：

对式（9）求导得：

在导弹飞向目标的过程中，有＜0，因此得：

将式（13）代入式（11），又因为期望弹目距离＞0，因此有：

即是负定的，因此，渐进收敛于零。

2.1.2 弹目距离协同制导律设计

根据时标分离原理［7－8］，可将由式（5）和式（6）描述的弹目相对运动非线性系统分解为2个快慢变化不同的子系统——慢变子系统（5）和快变子系统（6），然后利用动态逆系统理论对2个子系统分别进行反馈线性化，将原系统补偿为具有线性传递关系的系统，即伪线性系统［9］，再用线性系统的设计理论完成系统的综合与设计，从而导出弹目距离协同制导律。

2.1.2.1 慢变子系统动态逆设计

对于如式（5）所示的慢变子系统，其期望输出为，设其控制量输入为速度前置角指令ηc。为使系统的输出r→可令其具有如下的动态特性：

式中：kr＞0，为慢变子系统带宽。根据动态逆系统方法，综合式（15）和式（5），可得此子系统的期望输入为

式中：η0为η的初始值，sgn（·）为符号函数，式（16）表示ηc的符号与其初值η0相同。为了保证能求出ηc，必须满足：

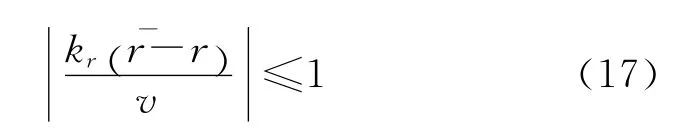
当速度前置角η跟随式（16）所示的前置角指令变化时，慢变子系统（5）将被补偿成为线性系统（15），其输出r渐进收敛于。假设η0＞0，分析式（16）（η0＜0情况类似）。当r＞时，ηc∈［0，π／2），此时，导弹速度在视线方向的分量使弹目距离缩短且趋近于期望弹目距离；当r＝时，ηc＝π／2，此时，导弹的速度矢量垂直于视线，其在视线上的投影为零，力图使弹目距离保持为当r＜时，ηc∈（π／2，π］，此时，要求导弹倒飞以增大弹目距离，使其趋近于；考虑实际情况和η0＜0的情况，为保证＜0，ηc的取值范围为（－π／2，π／2）。

根据时标分离原理，慢变子系统的期望输入ηc将作为快变子系统的期望输出，即快变子系统控制器的任务为：通过设定比例系数K控制η逐渐趋近于ηc。

2.1.2.2 快变子系统动态逆设计

对于快变子系统（6），其期望输出为ηc，控制量输入为K。根据动态逆系统方法，令

则快变子系统（6）可被补偿为伪线性系统：

式中：kη＞0，为快变子系统带宽。当按照式（18）设定比例系数K时，速度前置角η将渐进收敛于ηc，从而可实现对各导弹弹目距离的调整和控制。

将式（18）代入式（1）可得弹目距离协同制导律的表达式：

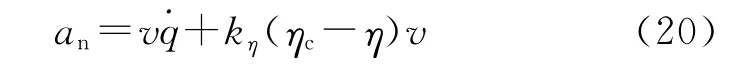
式中：ηc与当前时刻各枚导弹的弹目距离r有关。

由式（20）可见，当η→ηc时，此制导律变为比例系数K＝1的比例导引律。由式（6）知，此时＝0，即η为常数。随着弹目距离r逐渐减小，由式（4）和式（1）知逐渐增大，导弹的需用过载逐渐增大，最后趋近于无穷。当需用过载超过导弹的可用过载时，弹目距离协同制导律无法实现，导弹最终无法命中目标。如果在弹道末段，即r＜rε（rε为设定的制导律切换的弹目距离）时，设计一种制导律，在弹目距离逐渐缩短的过程中，能使→0，即η→0，则导弹能精确命中目标。而且，如果rε不大，而多枚导弹之间的速度相差又不太大时，其命中目标的时间差不会太大，即实现了多枚导弹攻击时间的协同，各导弹几乎同时命中目标。

2.2 视线角速度收敛制导律

在实现弹目距离协同和合理确定rε的基础上，根据有限时间控制理论设计an，使得在有限时间内快速收敛于零，保证导弹最终能命中目标。考虑如下引理：

引理1［10］一阶线性系统

可被下列控制器在有限时间内镇定：

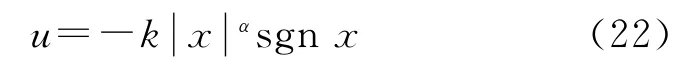
式中：x为状态变量，u为控制量，k＞0，0＜α＜1。引理1表明：对初始状态x（0）≠0的状态x（t），如式（22）所示的控制器将在有限时间ts内使状态变量到达x＝0（平衡点）后停留，且

当目标静止时，由式（2）和式（3）可得：

根据引理1，针对如式（24）所示的系统，可取控制量：

则η和将在有限时间ts内被镇定至零。需要说明的是，只有在保证弹目距离逐渐减小，即＜0的前提下，采用式（25）所示的制导律才能精确命中目标，而在弹目距离协同制导律中对速度前置角的限幅（ηc∈（－π／2，π／2））则保证了＜0这一条件。

综上所述，多枚导弹协同攻击目标时，使其飞行前段能够实现弹目距离协同、飞行末段能够精确打击目标且实现攻击时间协同的制导律为

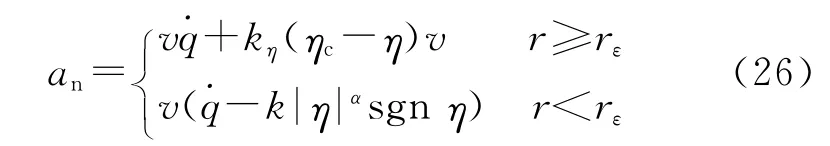
且ηc∈（－π／2，π／2）。

3 仿真分析

假设2枚导弹协同攻击一个舰艇，2枚导弹的初始状态如表1所示，表中下标0表示初始值，（xm，ym）表示导弹在地面坐标系的坐标。设2枚导弹作匀加速运动，其切向加速度均为aτ＝0.1m／s2。目标的位置为（45，25）（km）。取设计参数kη＝0.5，kr＝1，k＝50，α＝0.6，两部分制导律在弹目距离rε＝2 000m时切换。考虑到导弹逐渐飞向目标的需求以及能量和过载的约束，对速度前置角指令进行限幅：－20°≤ηc≤20°。另外，设2枚导弹的可用法向过载为±10。

表1 导弹的初始参数

为更接近于真实系统，设导弹法向加速度自动驾驶仪为一阶惯性环节，即

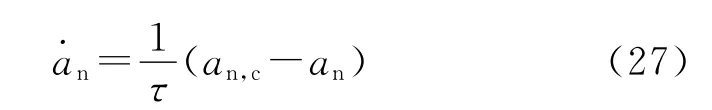
式中：τ为驾驶仪时间常数，取τ＝0.3s，an，c为法向加速度指令，由式（26）确定。仿真结果如图3～图9所示。图5～图7主要显示飞行前段应用弹目距离协同制导律时相关参数的变化情况，其余的图则显示了导弹整个飞行过程中参数的变化。

图3 导弹运动轨迹

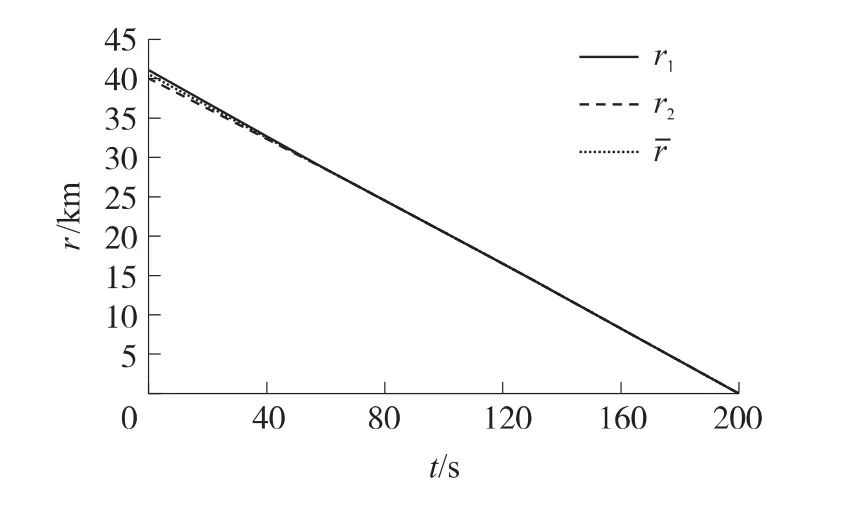
图4 弹目距离随时间变化

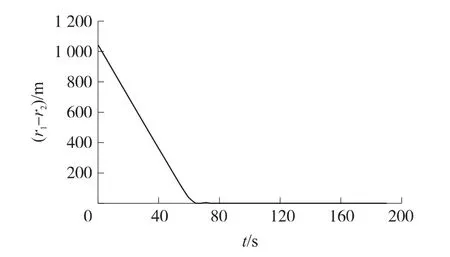
图5 弹目距离差随时间变化

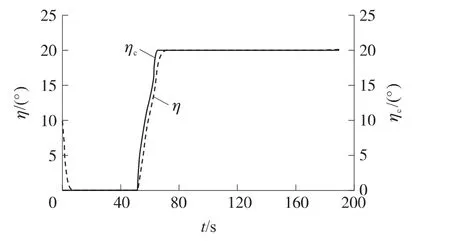
图6 导弹1的速度前置角变化

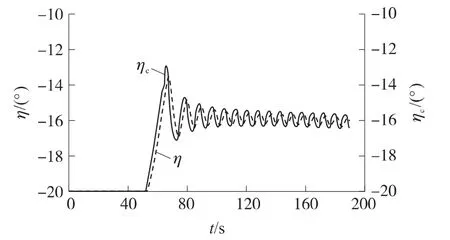
图7 导弹2的速度前置角变化

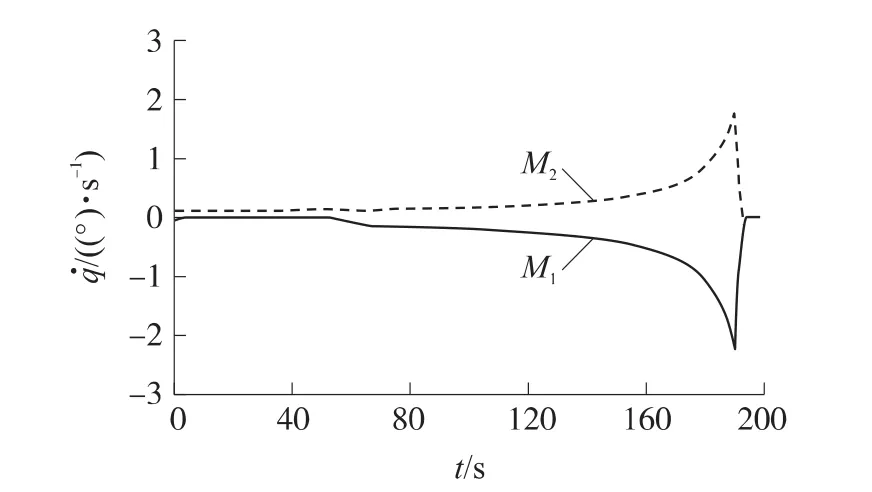
图8 视线角速度随时间变化

图9 法向过载随时间变化

对仿真结果进行分析：

①综合图5、图6和图7可知，开始飞行时，导弹1距目标比较远，因此，为了达到弹目距离协同，导弹1以最大相对速度（ηc＝0）飞行，而导弹2则按照限幅的最大（按绝对值）速度前置角飞行以等待导弹1，在78s左右，两弹的弹目距离相等，均等于期望弹目距离。在接下来的飞行过程中，由于导弹1的速度大于导弹2的速度，因此，导弹1的相对速度较小（速度前置角较大），其按照限幅最大的速度前置角飞行；导弹2则按照弹目距离协同的要求不断地调整其速度前置角。由图4和图5看出，78s后、切换制导律之前，两弹的弹目距离实现了很好的协同。另外，由图6和图7还可看出，实际的速度前置角η能够较好地跟踪前置角指令ηc。

②由于两部分制导律切换时的弹目距离比较小，而且2枚导弹的飞行速度相对较大且相差不多，因此，2枚导弹到达目标的时间差比较小，约为0.2s，可认为2枚导弹几乎同时攻击目标，实现了攻击时间的协同。

③在采用弹目距离协同制导律时，由于在78s前导弹1的弹目距离大于导弹2的弹目距离，因此导弹1在视线的方向上快速飞向目标，而在78s后，它的飞行速度大于导弹2，为了达到弹目距离协同，其绕路飞行，弹道相对弯曲。导弹2则是在78s前绕路飞行，而在后面一段快速接近目标。在采用使视线角速度收敛的制导律时，快速收敛，η快速收敛于零，导弹最终以直线弹道飞向目标。这些可由图3看出。

④由图8可见，在大约188s时，制导律进行切换。前一段应用弹目距离协同制导律时，在η→ηc的情况下，由式（20）可知，比例系数K→1，不满足比例导引律的收敛条件，因此，视线角速度发散。188s后，导弹按式（25）所示制导律飞行，视线角速度快速收敛。

⑤从图9所示的法向过载图中可知，在应用弹目距离协同制导律时，2枚导弹的法向过载比较小且变化平缓。在两部分制导律切换时，过载较大，但也不超过导弹的可用过载，之后过载快速收敛于零。因此，导弹的过载满足要求。

4 结束语

针对多枚导弹协同作战时导弹同时到达目标区域和同时攻击目标的要求，在各导弹速度不同且可变的前提下，本文提出了由弹目距离协同制导律和视线角速度收敛制导律组成的协同制导律。在飞行前段，通过合理设计比例系数K，控制导弹实现弹目距离协同。在弹道末段，基于有限时间控制理论设计制导律使得视线角速度趋近于零，实现了对目标的有效协同打击。采用本文的协同制导律，导弹能够有效地突破敌方的防御系统，对目标实施有力的协同攻击，因此，本方法具有广阔的军事应用前景。下一步的工作将是：对本文方法如何应用于目标运动和导弹在三维空间内攻击目标的情况进行深入研究。

［1］印桂生，陈怀友.近程防御武器系统可视化仿真研究［J］.哈尔滨工程大学学报，2010，31（2）：220－225.YIN Gui－sheng，CHEN Huai－you.Vegaprime based visual simulation of a close－in weapon system［J］.Journal of Harbin Engineering University，2010，31（2）：220－225.（in Chinese）

［2］张昆，薛晓春.反舰导弹饱和攻击的组织及实施［J］.飞航导弹，2006（11）：15－17.ZHANG Kun，XUE Xiao－chun.The organization and implementation of anti－ship missiles’saturation attack［J］.Aerodynamic Missile Journal，2006（11）：15－17.（in Chinese）

［3］JEON I S，LEE J I，TANK M J.Impact－time－control guidance law for anti－ship missiles［J］.IEEE Transactions on Control Systems Technology，2006，14（2）：260－266.

［4］赵世钰，周锐.基于协调变量的多导弹协同制导［J］.航空学报，2008，29（6）：1 605－1 611.ZHAO Shi－yu，ZHOU Rui.Multi－missile cooperative guidance using coordination variable［J］.Acta Aeronautica Et Astronautica Sinica，2008，29（6）：1 605－1 611.（in Chinese）

［5］张功，李帆，赵建辉，等.弹着时间可控的机动目标多弹协同制导律［J］.指挥控制与仿真，2010，32（1）：52－55.ZHANG Gong，LI Fan，ZHAO Jian－hui，et al.Impact－time－control guidance law for multi－missile cooperative model with mobility of the target considered［J］.Command Control ＆Simulation，2010，32（1）：52－55.（in Chinese）

［6］施建洪，张友安，梁勇.飞行器落角与撞击时间控制研究［J］.海军航空工程学院学报，2011，26（4）：398－404.SHI Jian－hong，ZHANG You－an，LIANG Yong.Research on impact angle control and impact time control for aircraft［J］.Journal of Naval Aeronautical Engineering Institute，2011，26（4）：398－404.（in Chinese）

［7］SCHUMACHER C，KHARGONEKAR P P.Stability analysis of a missile control system with a dynamic inversion controller［J］.Journal of Guidance，Control and Dynamics，1998，21（3）：508－514.

［8］苏身榜，张友安.动态逆方法在空空导弹控制系统设计中的运用［J］.海军航空工程学院学报，2003，18（6）：601－604.SU Shen－bang，ZHANG You－an.The application of dynamic inversion to control system design for air－to－air missiles［J］.Journal of Naval Aeronautical Engineering Institute，2003，18（6）：601－604.（in Chinese）

［9］李春文，冯元昆.多变量非线性控制的逆系统方法［M］.北京：清华大学出版社，1991：19－58.LI Chun－wen，FENG Yuan－kun.Multivariable nonlinear control of inverse system method［M］.Beijing：Tsinghua University Press，1991：19－58.（in Chinese）

［10］BHAT S P，BEMSTEIN D S.Finite time stability of homogeneous systems［C］／／American Control Conf.Evanston：American Autom Control Council，1 9 9 7：2 5 1 3－2 5 1 4.