基于增强型显式互补滤波的无人机姿态算法

马 力， 李天松， 阳荣凯， 黄艳虎

(1.桂林电子科技大学 信息与通信学院，广西 桂林 541004； 2.玉林师范学院 电子与通信工程学院,广西 玉林 537000)

微机电系统(micro-electro-mechanical system，简称MEMS)传感器因体积小、经济实惠、精度适中等优点被广泛应用于无人机捷联式惯性导航系统。惯导系统启动后，机体的初始姿态未知，利用有效信息解算得到初始姿态矩阵的过程称为惯导系统的初始对准。现有的对准方法分为静基座和动基座对准。静基座精对准是先进行解析式粗对准，再运用卡尔曼滤波估计初始误差角及传感器误差进行修正对准[1]。动基座对准实时记录载体的姿态变化，结合初始姿态的最优估计值，进而得到导航前一刻的姿态[2]。然而，MEMS传感器的精度不够高，并不适用现有的对准方法。采用四元数方法更新姿态，四元数初始值由捷联惯导的初始对准确定[3-4]，一些开源项目或文献对四元数初值赋予[1,0,0,0]T[5-6]，四元数微分方程初值不够精确，导致后续解算精度降低。文献[7-9]使用扩展卡尔曼滤波、无迹卡尔曼滤波和粒子滤波进行九轴数据融合，但是这几种算法计算量较大，流程复杂，工程应用较为困难。ECF算法[10]利用加速度计测量地球重力与通过姿态矩阵得到的地球重力作向量叉乘，得到误差通过PI运算修正陀螺仪x、y轴角速度，缺点是未修正z轴角速度，即未修正航向角。为此，在ECF算法基础上，利用磁强计测量的地磁场强度信息来修正陀螺仪z轴角速度，能有效提高航向角估计的精度，得到的航向角不存在漂移现象。

1 系统设计

系统采用STM32F407处理器为控制核心，GY-86模块包含惯性敏感元件MPU6050(加速度计和陀螺仪)和高精度磁强计HMC5883。MPU6050最高可测量±16gn(gn为重力加速度)，±2000°/s的角速度，具有良好的动态响应特性。HMC5883采用霍尼韦尔各向异性磁阻技术，具备高灵敏度和高可靠性，测量范围达±8.1 Gs，用于辅助测量航向角。通过I2C总线与主控通信，速率可达400 kHz/s。初始对准与姿态解算系统框图如图1所示。

图1 初始对准与姿态解算系统框图

2 初始对准

导航常用3个坐标系。1)机体坐标系(b系，xbybzb轴)：原点位于飞行器重心，xb沿飞机横轴指右，yb轴沿飞机纵轴指前，zb轴沿飞机竖轴，xbybzb构成右手直角坐标系，此坐标系与IMU本体系s重合。2)东北天地理坐标系(n系，ENU轴)：原点位于飞行器重心，E轴指东，N轴指北，U轴和重力g方向相反，取此坐标系为导航坐标系。3)地心惯性坐标系(i系，xiyizi轴)：原点位于地球中心，xi、yi在赤道平面内，指向恒星方向，xiyizi构成右手坐标系。

加速度计测量的是比力。若将加速度计平放在地面上，则其受惯性力为0，在竖直方向受到重力产生重力加速度g，忽略物体绕地球产生的向心加速度，则z轴加速度计的输入量为-g，“-”号表示竖直向下，x、y轴的输入量为0。在四轴飞行条件下，假设加速度计只测量重力加速度，忽略其他瞬时加速度。对于MPU6050加速度计，有以下关系式成立：

A=AADC/SA。

(1)

其中：AADC为加速度计ADC输出；SA为灵敏度；A为机体加速度，在四轴飞行条件下，也就是重力加速度在机体各轴的分量。

陀螺仪角速度关系式为

(2)

为了得到初始四元数，利用加速度计求俯仰角、横滚角，磁强计求航向角，并分别与陀螺仪融合得到精度相对较高的姿态角。对于三轴加速度计，设α1为加速度计x轴相对地平面的角度，α2为加速度计y轴相对地平面的角度，α3为加速度计z轴相对重力方向的角度[11]，有

(3)

其中：Ax、Ay、Az为加速度计3个方向的ADC输出。|α1|与|α3|相等，其意义为偏离程度相同。

按照姿态角的定义：俯仰角(pitch)为机体yb轴与地平面间的夹角，以飞行器抬头为正；横滚角(roll)为机体zb轴与包含机体yb轴的铅垂面间的夹角，以飞行器向右倾斜为正；航向角(yaw)为机体yb轴在地平面上的投影与N轴间的夹角，以机头右偏为正。由于s系与b系重合，有

θacc=α2，γacc=α1，

(4)

其中θacc为俯仰角，γacc为横滚角。

可由磁强计测得航向角，通过θ与γ对磁强计进行倾斜补偿[12]，在b系下，

(5)

其中：Mx、My、Mz为磁强计ADC输出；Hx、Hy为倾斜的磁强计回归水平方向的ADC输出修正值；ψ为航向角。在机体受到晃动干扰的情况下，单独使用式(4)、(5)计算精度较低，必须滤除干扰。为此，对加速度计ADC输出值进行滑动平均滤波，再用式(4)、(5)进行计算。对于仍存在的高频干扰，使用传统的互补滤波方法去除。

(6)

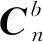
θgyro=ω·dt+θgyro。

(7)

对于θgyro初始值，用式(4)得到的角度代入。由于加速度计、磁强计具有高频噪声，通过上述方法求姿态角，虽然每次得出的结果精度稍低，但不会随时间产生累积误差；陀螺仪具有低频噪声，每次的角速度输出精度较高，但角度由于是积分得到，从而不断形成累积误差。为抑制陀螺仪积分累积误差、滤除加速度计和磁强计输出中的高频干扰，通过一阶互补滤波融合计算：

(8)

其中：τ为滤波器时间常数；ψ为航向角。

3 四元数姿态更新算法

3.1 四元数

2个坐标系间的位置关系可认为是刚体的定点转动，可用四元数描述。四元数是由4个元构成的数，

Q(q0,q1,q2,q3)=q0+q1i+q2j+q3k=

[q0,q1,q2,q3]T。

(9)

其中：q0、q1、q2、q3为实数；i、j、k为相互正交的单位向量。

(10)

(11)

将式(11)简化为

(12)

结合式(10)、(11)可得到四元数转换为姿态角的关系式：

(13)

在已知姿态角情况下，可通过姿态角转换为四元数，

(14)

由于

(15)

只要确定了q0的正负，其他3个数的正负也随之确定。由式(13)可知，若q0、q1、q2、q3的正负号全部取反，得到的姿态角不变，因此，q0的符号可任取正负。

东北天和北东地2个地理坐标系都可作为导航参考系，但是不同参考系下的计算公式略有不同，不能混用。

3.2 解四元数微分方程

用四元数方法更新姿态，归根结底是求四元数。可直接将四元数应用到程序中，或者先将其转换为姿态矩阵和姿态角。四元数微分方程

(16)

对于不具备特殊形式的常微分方程式，

(17)

假设其解为y(x)，在定义域内某区间[xi,xi+1]，使用微分中值定理，有

y(xi+1)-y(xi)=y′(εi)(xi+1-xi)，

(18)

其中εi∈[xi,xi+1]。记(xi+1-xi)为步长h，K=hy′(ε)，式(18)可改写为

y(xi+1)=y(xi)+hy′(εi)=y(xi)+

hf(xi,yi)=y(xi)+K。

(19)

将K视作在[xi,xi+1]上的平均斜率近似值，只要求出K，再利用初值y(m)就可迭代求解。为了获得更高的精度，在区间[xi,xi+1]内选择4个点，将这4个点的斜率进行加权平均，获取平均斜率误差较小的近似值K，这就是经典的4阶龙格库塔法(RK4)。

4 增强型显式互补滤波

式(8)是一阶互补滤波，求出角度后进行互补滤波，不必通过四元数求姿态角。由四元数描述的EECF算法是先将加速度计、磁强计数据融合至陀螺仪角速度信息中，以修正飞行器相对导航坐标系的角速度，再求修正四元数。

重力加速度g在地理坐标系的分量为

gn=[gx,gy,gz]T=[0,0,-g]T,

(20)

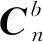
(21)

(22)

对式(21)和式(22)进行向量叉乘：

axsz,axsy-aysx)T。

(23)

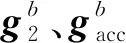
(24)

其中：Ki为积分系数；Kp为比例系数。由ωb,new可求出修正的四元数，并对其归一化处理得qnew。此时，将b系的任一向量经过新的姿态矩阵映射到n系，即将b系旋转到n系所在位置，则这2个坐标系的xOy平面是重合的。

显式互补滤波(ECF)算法的缺点是未修正航向角误差，可利用磁强计修正航向角误差，构成了增强型显式互补(EECF)算法，其原理如图2所示。

图2 增强型显式互补算法原理框图

磁强计测量的地磁场强度在机体坐标系的分量归一化为

mb=(mx,my,mz)T，

(25)

(26)

在北半球，任意一点的地磁场强度水平分量平行于地平面指向北，竖直分量竖直向下。设其在地理坐标系的投影为

d=(0,dy,dz)T，

(27)

其中dy和dz为未知量，取dy=uy,dz=uz，则

d=(0,uy,uz)T，

(28)

即mn的ux分量应为0。将式(26)与式(28)进行向量叉乘，得

merr=mn×d=(0,-uxuz,uxuy)T，

(29)

与式(24)类似，再次对ωb修正，得

(30)

5 算法验证分析

搭建以STM32主控、GY86模块、数传、电子调速器、遥控发射机与接收机等为核心部件的硬件平台，进行飞行试验。系统上电后，由STM32获取GY86模块的原始数据，设置采样率为100 Hz，采集初始对准以及姿态解算2个过程的数据，由数传模块传输至电脑端，通过MEX指令将Matlab与C语言混合编程，用本算法分析结果。初始对准在晃动条件下完成，初始对准的姿态角如图3所示，姿态解算的姿态角如图4所示。

图3 初始对准的姿态角

图4 姿态解算的姿态角

首先进行经初始对准与直接赋予四元数[1,0,0,0]T的姿态角对比，分别记为方式1、方式2，使用增强型互补滤波算法，以航向角为例，进行误差分析。四元数[1,0,0,0]T对应θ=0,γ=0,ψ=0，由初始对准得到的初始姿态角θ=-1.74°，γ=0.43°，ψ=20.13°，两者之间存在误差。图5为2种方式航向角估计值。从图5可看出，使用方式2相对方式1进行解算得到的航向角发生了偏移。

图5 2种方式航向角估计值

固定初始俯仰角和初始横滚角，变换初始航向角，观测姿态解算中航向角偏移量，如图6所示。从图6可看出，初始姿态角偏移越大，则解算得到的姿态角偏移越大。加入初始对准算法能得到初始姿态角，有助于提高后续姿态解算的准确性。为了比较算法的滤波效果，使用卡尔曼滤波以及MPU9250自带的DPM算法得到静态时的姿态角，采用姿态角标准差比较各算法滤波精度，静态姿态角标准差如表1所示。从表1可看出，EECF算法不仅能解算出机体的俯仰角和横滚角，还可解算得到航向角，静态姿态角标准差小于0.05°，且解算精度相比卡尔曼滤波、MPU9250 DMP滤波，航向角标准差分别下降了63.8%、35.4%。

图6 初始航向角与姿态解算中航向角偏移

算法θ/(°)γ/(°)ψ/(°)卡尔曼滤波0.0610.0620.116MPU9250 DMP0.0370.0340.065EECF0.0230.0210.042

6 结束语

针对中小型飞行器使用微机电系统(MEMS)器件无初始对准过程导致姿态估计精度低的问题，提出一种基于增强型显式互补滤波的无人机姿态算法。一方面，加入初始对准算法，可解算出初始航向角，提高了后续姿态解算的准确性；另一方面，在显式互补滤波(ECF)基础上，增加使用地磁场强度信息修正陀螺仪z轴角速度，构成了增强型显式互补滤波(EECF)，提高了航向角解算精度，得到的航向角不存在漂移现象。搭建硬件平台进行了算法验证，为后续实验提供了实践基础。