仿人机器人协调阻抗控制算法

齐春丽， 伍锡如

(桂林电子科技大学 电子工程与自动化学院，广西 桂林 541004)

近年来，仿人双臂机器人在操作空间内具有优越的协调操作能力，可以完成重型物体搬运、零件装配、焊接等复杂任务，已成为机器人领域的研究热点。自20世纪80年代起，国内外许多研究者开始了对双臂协作的研究[1-2]。

基于机械臂运动学和动力学模型，双机械臂协作的诸多控制算法被提出，主要包括位置控制、力/位混合控制、阻抗控制等[3]。李贺立等[4]提出了一种新型阻抗控制算法，将双臂看作主从臂，引入双臂间相对误差和虚拟恢复力概念，合理分配载荷，实现了双臂用于搬运柔性物体的需求，同时减小了双臂间误差，提高了系统的稳定性。Caccavale等[5]提出基于阻抗内环和阻抗外环相统一的整体控制算法，解决双臂的协调阻抗控制问题，并采用工业机器人进行实验验证，证明算法既能减小内应力，又能防止滑环现象的发生，克服了单一阻抗控制存在的缺点。敖天翔[6]将阻抗模型拓展为多点阻抗模型，并利用有限元理论对其求解，解决了双臂协调操作过程中运动与力协调的分配问题，实现操作系统的可靠性。Tao等[7]提出了位置控制模型和力控制模型2种控制方案，将二者应用于协作机器人同一相互作用方向上，并验证了控制方案的优越性。华磊等[8]提出一种扩展的冗余机械臂阻抗控制算法，该算法通过对操作空间和零空间共组的增广操作空间解耦，得出相应驱动力矩，并引入避关节极限性能指标函数来优化零空间运动，确保冗余关节运动角度的合理性。陈钢等[9]在双臂协调操作运动约束关系的基础上，提出了适用于协调操作的力/位混合控制方法，并通过实验与传统控制方法比较，验证了该方法的正确性。Duan Jinjun等[10]针对双臂协同时外部干扰和校准误差会引起未知轨迹偏差的问题，提出了一种用于力/位跟踪的对称自适应变导纳控制方法，该方法能够补偿偏差，减小其对系统的影响。

考虑到操作过程中干涉力会对双臂产生影响，许多研究者通过引入扰动观测器，以控制干涉力对双臂的影响。司彦娜等[11]采用非线性干扰观测器的自适应反演滑模控制方法，实现对机械臂轨迹跟踪问题的控制，保证系统稳定性。Sadeghian等[12]基于任务空间误差和机器人的广义动量，设计了2种不同的扰动观测器，以观测估计和补偿任务变量上的广义力，确保任务空间误差的渐近稳定性，并在七自由度机械臂上进行了实验验证。钱琮玮等[13]基于动量守恒设计了一种外部扰动观测器对机械臂碰撞的作用力进行预估，根据观测器观测结果的不同设计相应的响应控制方法，避免机械臂与机械臂和机械臂与外部干扰的碰撞。

为了实现既能观测对外部扰动，又可达到合理分配载荷的目的，保证物体搬运过程中的控制精度，考虑到操作物的运动特性，构建统一动力学模型，结合基于广义动量的扰动观测器观测外部扰动力矩，设计了适用于双臂协调的阻抗控制方法，同时引入变加权矩阵以求得最优抓取矩阵，达到协调操作过程中合理分配载荷的目的，提高操作系统的性能。

1 仿人机器人运动学模型

1.1 正逆运动学分析

多关节机器人是由多个连杆组成，各连杆之间通过相邻坐标的齐次变换(平移变换和旋转变换)实现机械臂末端位姿变换，完成预定工作。相邻坐标之间的变换通式为

(1)

其中qi、ai-1、αi-1、di为机械臂连杆相对应的D-H参数，分别表示各关节转角、连杆长度、相邻关节的扭转角、连杆偏移。根据D-H参数法可得2个七自由度机械臂末端相对于基座坐标系的位姿变换矩阵为

(2)

若已知机械臂末端位姿，求解机械臂各关节的转角变量的过程称为机械臂的逆运动学分析，逆运动学是正运动学的逆运算。

1.2 双臂运动学模型

采用n(n=7)自由度的Baxter仿人双臂机器人，其模型如图1所示，相应的关节空间动力学模型为

(3)

图1 双臂机器人模型

由于外力矩由机械臂末端受外力所产生的操作力矩分量μo和其他位置的扰动力矩分量μd组成，式(3)可改写为

(4)

通常，机械臂末端操作空间和关节空间的转换关系为

(5)

其中：x为机械臂末端位姿；J为雅可比矩阵。式(5)的另一种形式为

(6)

其中：J+为雅可比矩阵的广义逆矩阵；δ为任意n维向量。式(6)中前后两部分分别表示机械臂操作空间和零空间的运动动力学模型。

设零空间速度向量为v，雅可比矩阵为JN，两变量约束条件为

(7)

1.3 双臂与操作物统一动力学模型

仿人机器人紧协调时双臂与操作物之间的约束及受力关系如图2所示。其中：Ol和Or分别为左右臂在操作物上的抓取点；Oc为操作物质心；Of为仿人机器人基座坐标原点；ftl、ftr、τtl和τtr分别为双臂末端输出力和左右臂输出力矩；m0g表示操作物体的重力。

图2 仿人机器人紧协调操作约束及受力关系

根据紧协调操作特性，当忽略操作物形变时，O、Ol和Or处的速度、加速度均相等。操作物质心处所受合力表达式为

(8)

由牛顿-欧拉方程，操作物动力学方程为：

(9)

其中：Io为操作物惯性矩阵；ωo为操作物角速度。由式(8)、(9)可变换为

(10)

其中：W为双臂协调操作是的抓取矩阵；Mo为常数矩阵；Co为反对称矩阵。

根据式(10)，双臂作用在操作物质心的操作力为

Ft=W+(Fo-Fto)+(I12-W+W)Ωd=

(11)

(12)

用Ft代替式(7)中的J+Tμo，在满足双臂紧协调操作特性的基础上，仿人双臂机器人与操作物的统一动力学模型为

(13)

2 带有扰动观测器的双臂阻抗控制

2.1 双臂阻抗控制

阻抗控制可以很好地控制机械臂和环境之间的相互作用，能够实现机械臂协调操作的稳定性。冗余双臂关节空间阻抗方程式为

(14)

其中：qd为机械臂的期望轨迹；Md、Bd和Kd分别为关节期望惯性、期望阻尼和期望刚度。式(14)的对应控制输入为

(15)

采用期望内力Fid和调节系数L实现操作物内力平滑变化。为控制操作物内力，设操作物期望位姿为xd，根据式(13)，机械臂操作空间阻抗方程为：

(16)

其中：Mx、Bx和Kx分别为操作物期望惯性、期望阻尼和期望刚度。式(16)相应的控制输入为

Kx(xd-xo)]。

(17)

(18)

根据式(18)，可知零空间的阻抗方程为

(19)

其中Mv、Bv和Kv分别为零空间中期望惯性、期望阻尼和期望刚度。由于零空间位置误差不易定义，由文献[14]可知，经投影的关节空间误差能被用来定义零空间所要求的输入加速度，

(20)

2.2 基于广义动量的扰动观测器

未知环境对机械臂产生的外部扰动干涉力对机械臂运行的轨迹精度有很大的影响，为了提高机械臂运动精度，增加机械臂稳定性，设计了基于广义动量的能观测扰动干涉力矩μd的控制器。

根据统一动力学模型(13)，定义机械臂的广义动量为

(21)

则

(22)

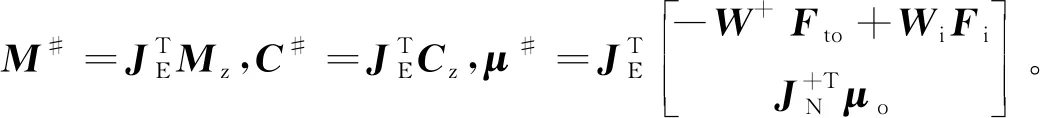
令残余向量r作为观测器指标，其表达式为

(23)

则

(24)

其中Kr为正定对角线矩阵。特别地，P(0)=0，r(0)=0。

当存在干涉力时，观测器指标会快速增加到-μd，根据外力矩的变化而变化，实现对干涉力矩的观测。结合式(23)和式(17)，用残余向量代替扰动力矩μd，式(17)可改写为

Kx(xd-xo)]。

(25)

(26)

该控制律能控制操作物运动和内力分配，解决因干涉力导致的机械臂运行精度下降问题，保证紧协调操作过程中机械臂及操作物的稳定运行。

设计合理的抓取矩阵，可直接控制分配载荷及内应力的大小。定义W+为

(27)

机械臂在紧协调搬运时的总驱动能量为

ξ=0.5μTμ。

(28)

若要合理分配抓取载荷，则需要对式(28)进行最小优化处理。采用KKT条件对其进行最优化[15]，引入变加权矩阵实现了抓取载荷的合理分配，且能控制操作物内应力的大小，使操作系统性能达到最优。

3 实验结果与分析

为了验证本算法的正确性，采用七自由度的双臂机器人为模型，利用Matlab软件平台进行仿真实验。表1为其中一个机械臂的D-H参数。

表1 双臂D-H参数表

仿真时将2个机械臂的初始关节角分别设置为ql=[-π/20π/6π/2-π/1.4π0]和qr=-ql，机械臂的终止关节角度为ql=[-ππ/2π/2π/3.5-π/60π/8]，操作物体的质量为4 kg，操作时间为40 s，时间间隔为0.05 s，阻抗控制参数分别为Bx=16E6，Kx=0.2E6，Bv=1.5E14，Kv=16E14。

图3为无观测器时操作物体的位置误差。从图3可看出，当无观测器时，操作物体的位置误差比较大。图4为有观测器时操作物体的位置误差。比较图4、图3可看出，引入观测器后，操作物体的位置误差远远小于无观测器的位置误差，表明操作物体位置精度有很明显的提高。

图3 无观测器时操作物体的位置误差

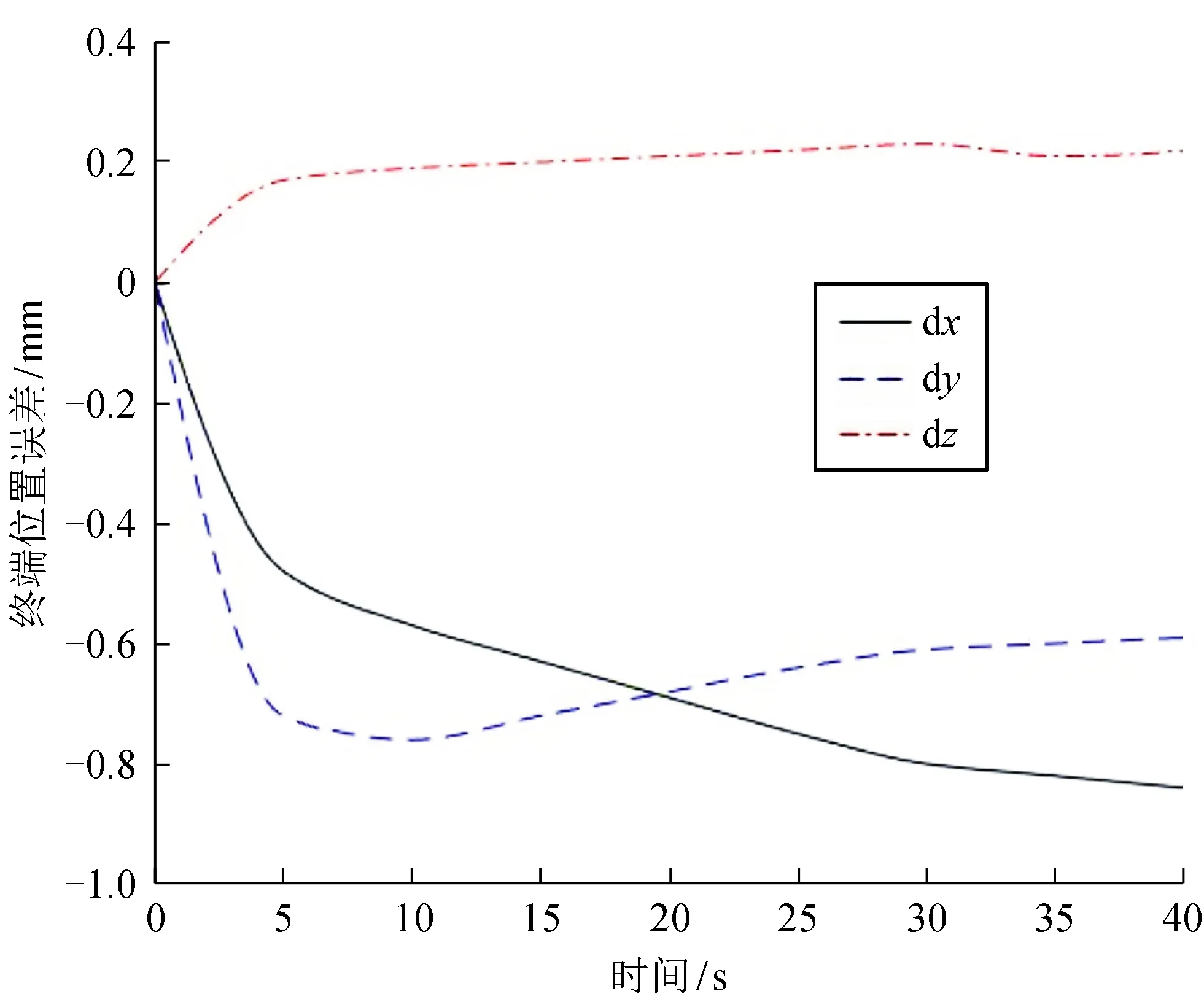
图4 有观测器时操作物体的位置误差

图5 机械臂的实际关节力矩

图6 观测器观测的关节力矩

图5为机械臂的实际关节力矩，图6为观测器观测出的关节力矩。对比图5、6可看出，10 s时存在外干涉力条件下，观测器观测的关节力矩与实际关节力矩基本一致，说明了本观测器是有效的。

4 结束语

针对仿人双臂机器人在未知环境下协调操作时操作物和机械臂轨迹跟踪精度低的问题，在阻抗控制方法的基础上，提出了双臂紧协调的控制算法。通过分析紧协调操作时物体与双臂存在的约束关系，建立两者统一动力学模型。同时，为了使机械臂达到节约工作资源、优化分配载荷的目的，引入变加权矩阵。为了能实现对未知环境干涉力的直接控制，采用能观测外部干涉力的扰动观测器，使其与阻抗控制模型结合，设计了仿人双臂机器人的协调阻抗控制算法，提高了操作物的位置跟踪精度，极大地改善了协调操作的性能。