三轴磁强计及梯度计校准的综合系数法

徐超群，张绍华，易 忠,2*，孟立飞

（1.北京卫星环境工程研究所；2.可靠性与环境工程技术重点实验室：北京100094）

0 引言

三轴磁强计是一种测量磁场大小与方向的仪器，常被用于磁性研究；由于其体积、质量和功耗都比较小，有时也被用于微小卫星的姿态控制[1-2]。磁场梯度计是由2个理论性能一致的磁强计构成，它的测量结果为2个磁强计的差分值，其特点在于测量结果更能反映被测物的磁性特征，并且在一定程度上自动过滤背景磁场的干扰[3-4]，因此在国防军工、科研生产等领域都有广泛应用。一般情况下，磁强计在加工生产过程中，会出现三轴不正交、零位不一致、三方向灵敏度不相同等问题；梯度计也会因2个磁强计摆放的线性位置不正确而引起误差[5]。这些都会严重影响它们的测量性能，因此在使用三轴磁强计和梯度计之前应该对其进行校准。

磁强计测量误差校准方法有很多种，如：利用磁强计的测量结果，分析计算误差，从而得到三轴磁强计的校准模型[6]；利用椭球曲面模型，计算磁场强度大小，由递推法计算校准参数[7]；最小二乘算法也是磁强计校准模型常用方法[8-10]；也有将粒子群算法和遗传算法等优化算法用于三轴磁强计的校准[11-12]，并且取得较好效果；还有一些星用磁强计使用在轨实时校准的方法[13]。梯度计的校准方法主要是对单个磁强计进行校准，或者通过坐标变换对2个磁强计摆放位置不一致引起的误差进行修正。以上校准方法大多需要考虑多个因素，测量过程和数据处理较为复杂。

本文在分析三轴磁强计及其组成的梯度计的测量误差特点与性质的基础上，建立测量误差修正模型，提出综合系数法，即：利用无磁转台把待校准的磁强计放入空间分布均匀且稳定的磁场中，通过测量不同组磁场数据，拟合出磁强计误差补偿矩阵，最后得出校正后的磁场结果。利用此方法对Bartington 公司生产的三轴磁强计及其组成的梯度计进行标定，以验证该方法的有效性。

1 误差分析

误差按照其产生的特点与性质，可分为粗大误差、随机误差和系统误差3种[14]，其中系统误差是可以补偿的。造成磁通门磁强计系统误差的主要因素是安装误差和制造误差。

1.1 零位误差

在零磁场环境，由于磁强计制造工艺等影响，磁强计测量结果不为零，这就产生了零位误差。只考虑电路漂移以及铁芯剩磁的情况下，三轴磁强计实际输出值和理论输出值的关系可表示为

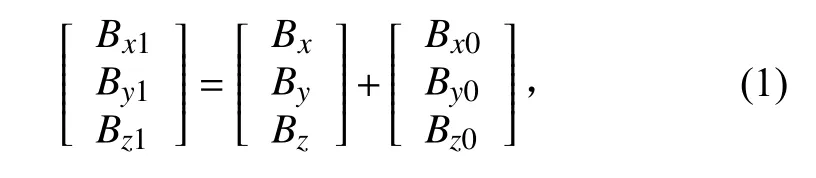
式中：Bx1、By1、Bz1为磁强计实际输出信号；Bx、By、Bz为磁强计理想输出信号；Bx0、By0、Bz0为磁强计初始值，即零位误差项。当Bx0=By0=Bz0=0时，测量结果为理想值。

1.2 灵敏度误差

理想状态下，磁强计的激励电路和三方向的磁敏部件在工作时其灵敏度是相同的；但是由于制造工艺的差别，三方向的灵敏度会存在差异，从而使测量结果不准确。这里用Kx、Ky、Kz分别表示3个方向的灵敏度，则磁强计3方向实际测量结果的表达式为

如果取Kx=Ky=Kz=1，则为理想状态。

1.3 正交误差

在实际加工生产中，磁强计的实际坐标系和理论坐标系存在一定差异，并且，三轴磁强计自身的三个坐标轴也不能完全正交[15]。如图1所示，假设磁强计的理论正交坐标系为Oxyz，其真实的三轴坐标系为Ox1y1z1，真实输出值为Bx1,By1,Bz1。

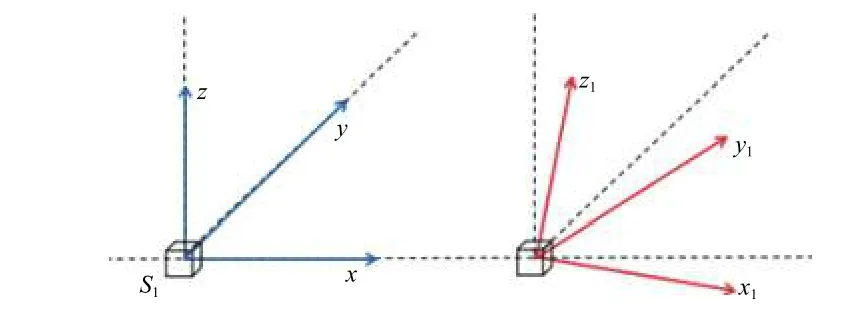
图1 坐标系三轴关系示意图Fig.1 The rectangular coordinateof the magnetometer

不正交性使得磁强计三轴之间存在误差。设：x1轴与正交坐标系的x、y、z轴的夹角分别为αx、αy、αz；y1轴与正交坐标系的x、y、z轴的夹角分别为βx、βy、βz；z1轴与正交坐标系的x、y、z轴的夹角分别为γx、γy、γz。除去其他因素，磁强计只有正交误差时，磁强计的输出信号应为

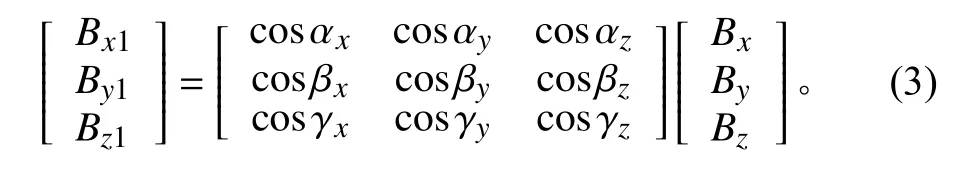
当αx=βy=γz=0，αy=αz=βx=βz=γx=γy=90°时，输出为理想状态。

1.4 梯度计误差

梯度计是由2个性能接近的三轴磁强计组成；假设每个磁强计都经过校准，属于理想型，则梯度计的误差主要是由2个磁强计的摆放位置引起。以其中一个磁强计为测量参考基准，第二个磁强计输出信号校准公式与正交误差校准形式一致。

2 校准方法

为了补偿误差，对以上几种影响误差的因素进行研究和分析，从而得到共有的影响形式。由上面的误差形式可以看到：

1）校准计算时，实际输出信号可从理想测量结果经由一个3×3阶的矩阵转换得到，如正交误差、灵敏度误差和梯度计的位置误差；

2）校准计算时，理想输出信号和实际输出信号相差一个常数，如零位误差。

将以上两种因素综合考虑，磁强计的理想输出信号和实际输出信号的关系为

其中M为磁场多元函数。对式(4)取平方，得到总场模值的平方：

在稳定磁场环境下转动磁强计，记录n(n＞12)姿态下磁强计输出值，采用最小二乘法，上述问题变为多元函数极值问题，因为B1是在不同姿态下采集，且采集数据量远远大于12，因此所求矩阵系数非奇异，存在唯一解。

3 实验验证

如图2所示，把校准系统放置于磁场均匀分布且正交稳定的CM2零磁试验室（属于北京卫星环境工程研究所），将2只三轴磁强计（Bartington 公司生产）组成的梯度计固定于无磁转台上，坐标系与CM2试验室坐标系一致，施加单方向的磁场，其他两个方向设置零场，利用钾光泵磁强计监测背景场，通过旋转转台，记录同一点的x、y和z三个方向测量的32组数据，B1为磁强计在不同旋转角度下的实际读数，B的理想值可以通过高精度光泵磁强计获得，或者通过测量得到的B1取平均得到，根据式(4)和式(5)，计算出系数矩阵。

图2 三轴磁强计校准验证实验Fig.2 Experiment for verification of three-axis magnetometer

3.1 三轴磁强计校准

先对组成梯度计的1号和2号磁强计进行校准，利用综合系数法分别计算出A和B0。其中：A为正交误差、灵敏度误差等因素的综合校准系数矩阵；B0为理想输出信号和实际输出信号相差的常数矩阵。则1号磁强计的待测系数为

2号磁强计的待测系数为

图3(a)和图3(b)分别为1号和2号磁强计总场校准结果。可以看到，未经过校准的磁强计测量值波动很大，利用综合系数方法校准后，2号磁强计的最大总场偏差从552.4 nT降到15.0 nT，2个磁强计的总场测量偏差降低了2个数量级。

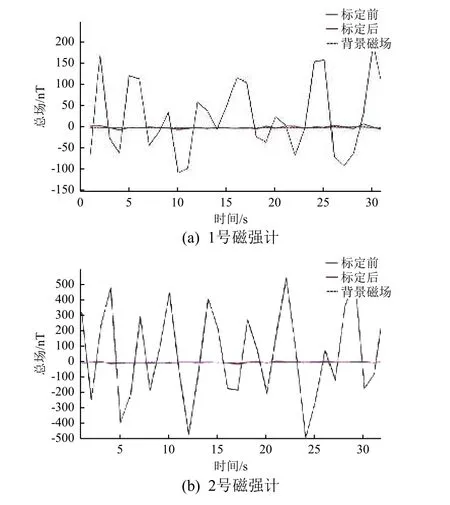
图3 2个磁强计的总场校准结果对比Fig.3 Calibration results of total magnetic field intensity for two magnetometers

3.2 梯度计校准

在对2个磁强计的零偏、灵敏度和非正交性偏差进行综合矫正后，将这2个磁强计组成梯度计。因为在安装时难以保证磁强计各个分量之间保持完全一致，所以需要对磁强计的各分量一致性进行标定，标定方法与单个磁强计的标定类似。在CM2零磁试验室启动大型线圈设备来抵消地球磁场，而后设置50 000 nT的竖向稳定磁场，把梯度计置于三轴无磁转台中心，并在360°球域空间旋转。以1号磁强计为参照，计算出2号磁强计对应的转向偏差矩阵，其待测系数矩阵A为

梯度计在x、y、z方向的校准结果对比如图4所示。可以看到，梯度计未校准前的测量偏差很大；经过校准之后，磁场梯度各分量测量精度提升了3个数量级。

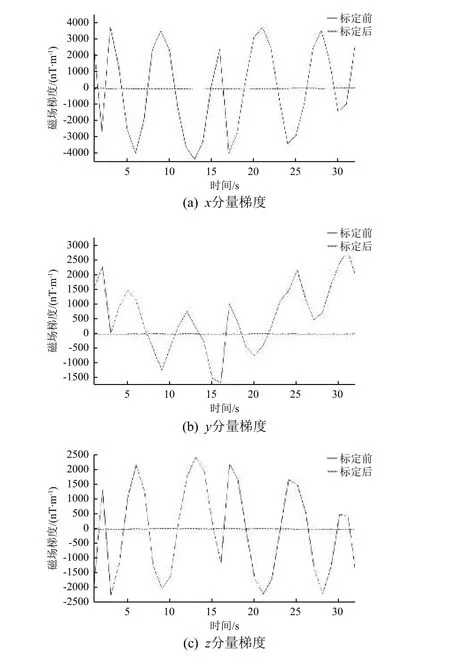
图4 磁场梯度计校准结果对比Fig.4 Comparison of calibration results of the magnetic field gradiometer

表1为磁传感器测量偏差最大值。可看出，经过校准后，测量偏差大幅度下降，说明该算法对磁强计和梯度计校准是有效的。实验结果没有达到偏差绝对值为0的校准效果，主要原因是监测背景读数与理想值之间存在一定差异；另外，转台旋转角度和读数的偏差，以及实际测量地点存在一定的磁场梯度，这些也会影响校准结果。

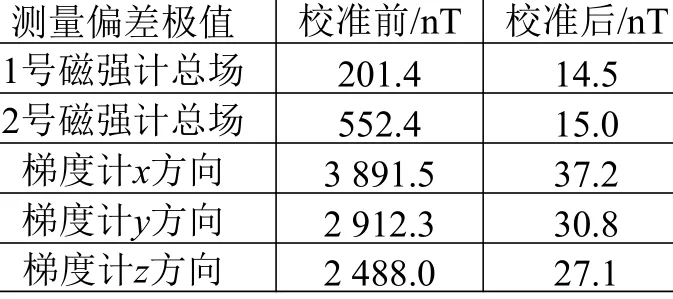
表 1校准前后磁场偏差极值对比Table 1 Comparison of peak values of magnetic field deviation before and after calibration

4 结束语

本文对磁通门三轴磁强计及其组成的梯度计的测量误差进行了分析，并根据误差特点与性质，建立了误差修正模型和校正算法；在均匀的磁环境中，利用无磁转台对三轴磁强计及其组成的梯度计进行了标定；实验结果证明该方法可将测量偏差降低2个数量级左右。此外，该方法还可用于对多个磁强计阵列进行校准，整个过程不需要单独计算每个磁强计零偏、灵敏度和非正交性偏差干扰因素，提高了三轴磁传感器的测量精度和效率。