基于最小二乘法的改进卡尔曼滤波算法

符 强， 陈孝倩， 孙希延， 任风华， 严素清

(1.桂林电子科技大学 广西精密导航技术与应用重点实验室,广西 桂林 541004；2.桂林电子科技大学 电子工程与自动化学院，广西 桂林 541004)

在室内、密集街区、山地、森林等微弱卫星导航信号环境中，由于遮挡和反射，卫星信号功率衰减并伴有多径干扰和噪声干扰，从而降低了码环的跟踪性能[1-2]。针对这些问题，现有的解决方案主要有3类：1)信号接收天线的空域处理方法，如扼流圈天线可以削弱来自地面和低仰角的多径信号[3-4]；2)对跟踪环路的相关器和码鉴相器进行改进，如窄相关[5]和Strobe鉴相器[6-7]，这类方法虽然可提高抑制多径干扰的性能，但也减弱了环路的跟踪性能和噪声抑制性能；3)基于估计原理的多径估计方法，如Townsend等[8]采用多相关器结构得到多组相关值，通过迭代计算，得到估计的直达信号相关参数，以达到抑制多径的目的。通过借鉴多径估计延迟锁定环路(MEDLL)中信号估计的方法，崔艳等[9]提出最大似然估计算法，利用最大似然估计原理在相关前估计出直达信号和多径信号的各项参数，虽能很好地抑制了多径，但也降低了噪声抑制性能，且有计算量过大的问题。基于卡尔曼滤波的方法很多，其主要有2种实现结构：1)在码环鉴别器和环路滤波器之间加入卡尔曼滤波器；2)用卡尔曼滤波器代替原有的鉴别器。卡尔曼滤波主要有线性卡尔曼滤波[10](Kalman filter，简称KF)、扩展卡尔曼滤波[11-12](extended Kalman filter，简称EKF)和平淡卡尔曼滤波[13](unscented Kalman filter，简称UKF)3种，其中EKF和UKF都是非线性的。采用非线性卡尔曼滤波虽然效果相对较好，但计算量很大；而采用线性卡尔曼滤波，计算量小，但存在滤波器发散的问题。

虽然研究者提出了很多基于卡尔曼滤波的码跟踪方法，但不管采用线性卡尔曼滤波还是非线性卡尔曼滤波，在这种滤波估计中，观测值是唯一的信息源，但信息源中的噪声误差、系统误差、观测误差、设备误差等会降低滤波器的估计性能，使得采用现有卡尔曼滤波技术的码跟踪环的性能较差。为此，提出一种最小二乘算法与卡尔曼滤波相结合的改进算法。

1 卫星导航信号模型与构造

卫星导航接收机中，载波跟踪环和码跟踪环共同组成接收机的跟踪环路。载波跟踪环对载波频率和载波相位进行跟踪。码环对码相位进行精确的估计和跟踪，这是实现伪距测量和定位的基础[14]。在存在多径效应的弱信号环境中，全球定位系统(global position system，简称GPS)卫星信号可表示为

(1)

其中：i为各路信号分量；ai为信号幅度；ω为载波频率；θi为第i路信号的载波初相位；c(t)为伪码；τi为第i路信号与本地伪码的码相位差；D(t)为导航电文；n(t)为高斯白噪声。这里τ0为直达信号与本地伪码的码相位差，是估计的目标参数。

设I路本地载波为sin(ω0t+θ0)，不考虑导航电文，则I路解扩后的相干积分值为

(2)

其中：

(3)

φi=(ω-ω0)Tcoh+(θi-θ0)；

(4)

(5)

其中：p(t)为服从N(0，σ2)的高斯白噪声；Tcoh为相干积分时长；fe为载波频率差；φi为载波相位差；Rc(·)为伪码自相关函数。实际接收机中，由于载波跟踪环对载波频率差fe和载波相位差φi的精确跟踪，将fe、φi看作已知的常数参数。

采用卡尔曼滤波器代替传统码环鉴别器处理多径问题，通常建立状态方程和观测方程，对直达信号和多径信号的码相位等目标参数进行估计，抑制多径效应。在这种方法中，由各相关支路解扩后的相干积分值组成的观测值是卡尔曼滤波的唯一信息源。从式(2)可知，伪码自相关函数是相干积分值的一个因子，这个因子包含噪声误差、系统误差、观测误差、设备误差等各种误差，这些误差会被带入卡尔曼滤波对目标参数的估计中。如何寻求一种方法抑制或消除这些误差，对自相关函数因子进行修正，使得观测值更接近真实值，从而对直达信号和多径信号的码相位、幅度等目标参数进行更精确的跟踪。

2 对相关函数因子的修正

为了便于推导，以接收到的卫星信号只包含一路直达信号和一路多径信号的情形为例，推导的结果很容易推广到更多路径的情况。设某一I路相关支路的相关器与本地即时码相关器的码相位间距为δ，由式(2)可知，该支路的相干积分值为

R(t)=a0sinc(feTcoh)cos(φ0)Rc(τ0-δ)+

a1sinc(feTcoh)cos(φ1)Rc(τ1-δ)+p(t)，

(6)

每次相干积分值作为一个观测值缓存于缓存模块中，每M次相干积分进行一次环路更新。式(6)可写成矢量形式

R=G·B+P。

(7)

其中：P为噪声矢量；R为该相关支路的M次相干积分值组成的观测矢量；G为量测矩阵；B为待估计的状态矩阵。

R=[R1,R2,…,RM]Τ，

(8)

(9)

(10)

由最小二乘估计原理[15]可知，B的最小二乘估计为

(11)

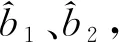
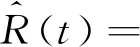
(12)

得到一个修正后的相干积分。对每条相关支路的相干积分中的自相关函数因子都用最小二乘算法进行修正，并得到修正后的相干积分，则可得一组无偏、均方误差和最小的新的观测值，组成观测矢量zk，用于后续的滤波估计。

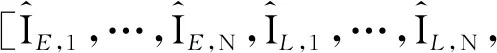
(13)

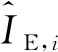
3 改进后的卡尔曼滤波在码跟踪中的应用

3.1 基于改进卡尔曼滤波的信号跟踪模型

利用最小二乘算法修正相关函数因子的思想，构造一组无偏、均方误差和最小的修正观测值。改进卡尔曼滤波算法的码跟踪环实现结构如图1所示。与传统卡尔曼滤波算法不同，改进卡尔曼滤波算法在卡尔曼滤波器前加入最小二乘模块，并在最小二乘模块与积分累加器之间加入缓存模块，用于缓存各支路解扩后的相干积分。为解决卡尔曼滤波器的发散问题，改进卡尔曼滤波算法加入了发散判断控制模块。

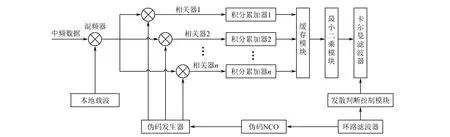
图1 改进卡尔曼滤波算法的码跟踪环实现结构

设各相关支路的相关器相对即时码相关器的码相位间距为±δj，为了能够估计多径信号，并对直达信号进行精确码跟踪，选择滤波器状态量为

x=[a0a1τ0τ1]Τ。

(14)

其中：a0为直达信号的幅度；a1为多径信号的幅度；τ0、τ1分别为直达信号和多径信号相对本地伪码的码相位差。卡尔曼滤波器的状态方程为

(15)

其中：wk为过程噪声向量，其为零均值白高斯噪声。设Qk是wk的协方差矩阵，Qk一般取对角矩阵，建立修正观测矢量与状态量之间的线性方程为

zk=Hk·xk+vk。

(16)

其中：Hk为测量矩阵,Hk的维数为4N×4；vk为测量噪声向量。Hk的第i列(i=1,2,3,4)可由下述公式求得，

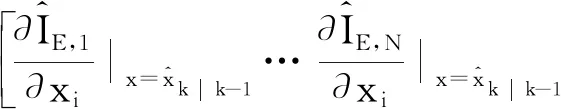
(17)

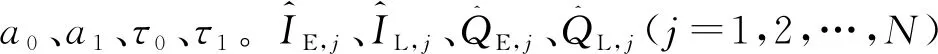
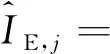
a1sinc(feTcoh)cos(φ1)Rc(τ1+δj)。

(18)

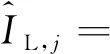
a1sinc(feTcoh)cos(φ1)Rc(τ1-δj)。

(19)

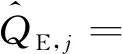
a1sinc(feTcoh)sin(φ1)Rc(τ1+δj)。

(20)

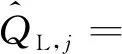
a1sinc(feTcoh)sin(φ1)Rc(τ1-δj)。

(21)

3.2 卡尔曼滤波器模块

设I和Q支路分别采用了N组超前-滞后相关器，考虑下线性系统：

xk=F·xk-1+wk；

(22)

zk=Hk·xk+vk。

(23)

根据系统模型构建卡尔曼滤波基本方程：

(24)

Pk|k-1=FPk-1FΤ+Qk-1，

(25)

Kk=Pk|k-1HkΤ(HkPk|k-1HkΤ+Rk)-1，

(26)

(27)

Pk=(I-KkHk)Pk|k-1。

(28)

在卡尔曼滤波的实现过程中，测量噪声的预测是非常关键的一步，很大程度上决定了卡尔曼滤波器的性能。此外，如何进行发散的判断和修正也是至关重要的步骤。只有这样，所设计的卡尔曼滤波器才能带来预想的效果。

1)噪声的理论分析。接收机中噪声是白高斯噪声，白高斯噪声通过积分累加器的过程可近似为通过低通滤波器的过程，故接收机噪声方差σ2=N0Bn/2，其中N0为双边带频谱功率密度，Bn=1/Tcoh为积分累加器的带宽。测量噪声协方差阵Rk由各测量之间的协方差组成。设n1、n2为I路上2条相关支路的信号，n3、n4为Q路上2条相关支路的信号，vn1、vn2、vn3、vn4为4条支路的噪声，|ni-nj|为2个信号所在支路相关器之间的码相位间距，

E[vn12]=E[vn22]=E[vn32]=E[vn42]=σ2。

(29)

由于I支路与Q支路的不相关性，有

E[vn1,vn3]=E[vn1,vn4]=E[vn2,vn3]=

E[vn2,vn4]=0。

(30)

设伪码码元长为Tchip，不同信号间的协方差为：

(31)

(32)

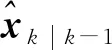
4 仿真结果与分析

采用GPS的1号卫星的伪码，中频为4.092 MHz，采样频率为16.368 MHz，相干积分时间为5 ms，每10次相干积分组成最小二乘模块的观测量。仿真有两路信号，一路直达，一路多径，多径信号相对直达信号的码相位时延为0.3码片，幅度相对比例为0.5。

图2为信噪比RSN=-25 dB时传统卡尔曼滤波算法[10]和改进卡尔曼滤波算法的码相位跟踪误差。从图2可看出，当RSN=-25 dB时，传统卡尔曼滤波的码相位跟踪误差为-0.028～0.031码片，改进卡尔曼滤波算法的码相位跟踪误差为-0.022～0.018码片，改进卡尔曼滤波算法的码相位跟踪精度稍高于传统卡尔曼滤波算法。

图2 2种算法在信噪比为-25 dB时码相位误差对比

图3为典型低信噪比RSN=-45 dB时2种算法的码相位跟踪误差。从图3可看出，随着信噪比降至-45 dB，传统卡尔曼滤波算法[10]的码相位跟踪误差为-0.14～0.17码片，而改进卡尔曼滤波算法的码相位误差为-0.06～0.08码片，改进卡尔曼滤波算法的码跟踪精度明显高于传统卡尔曼滤波算法。

图4为2种算法不同信噪比的码相位均方根误差(root mean square error，简称RMSE)。从图4可看出，在信噪比为-45 dB时，改进卡尔曼滤波算法和传统卡尔曼滤波算法[10]的码相位RMSE分别为0.002 7码片和0.043码片，前者比后者要小很多。随着信噪比的增加，2种算法的码相位RMSE都有减小的趋势。当信噪比增加到-24 dB时，改进卡尔曼滤波和传统卡尔曼滤波的码相位RMSE分别为0.001和0.004，相比于信噪比-45 dB的情形，2种算法的码相位RMSE的差值减小，但前者仍然小于后者。其结果充分表明了改进卡尔曼滤波算法较传统卡尔曼滤波算法的码跟踪性能更稳定。

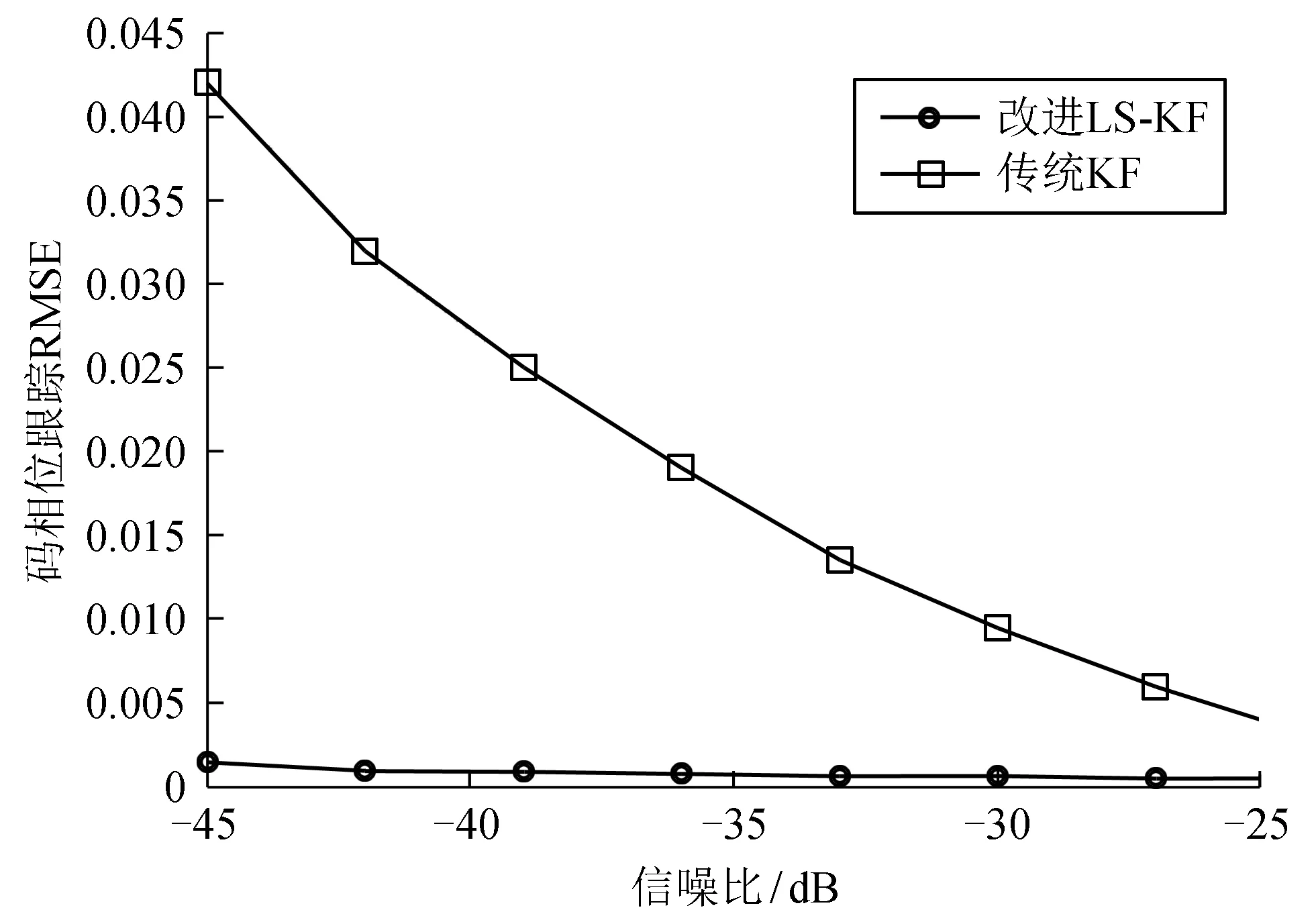
图4 2种算法在不同信噪比下的码相位跟踪RMSE对比

为了进一步分析2种算法在不同多径时延下的性能，仿真的2路信号中，多径信号相对直达信号的幅度为1/2。图5为2种算法在信噪比-45 dB和-25 dB时不同多径时延下的码相位RMSE跟踪误差。从图5可看出，在多径时延相同信噪比条件下，改进卡尔曼滤波算法比传统卡尔曼滤波算法[10]的码相位RMSE更小。改进卡尔曼滤波算法比传统卡尔曼滤波算法具有更优的跟踪性能。

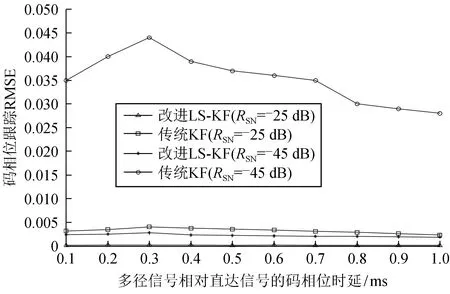
图5 2种算法在不同多径时延下码相位RMSE对比

5 结束语

为了解决卡尔曼滤波处理伴有多径干扰的微弱卫星导航信号的码跟踪时相干积分值组成的观测量误差较大的问题，利用最小二乘算法对相关函数因子进行修正的思想，构造一组无偏、均方误差和最小的修正观测值，建立数学模型，通过卡尔曼滤波得到更优的码跟踪性能，减小了相干积分中包含的多种误差，且采用线性卡尔曼滤波器，具有计算量小的特点。本算法加入了发散判断控制模块，控制了卡尔曼滤波器的发散。仿真结果表明，与文献[10]的算法相比，本算法对码相位跟踪具有更高的精度，特别是在低信噪比条件下，本算法的码相位跟踪误差精度与强信号条件保持在同一个数量级,同时具有更稳定的跟踪性能。在多径时延变化的统计意义上，本算法的码相位RMSE跟踪误差更小，具有更优的跟踪性能。