用法向量求二面角大小的一个问题

湖北省襄州一中 李继武

在用法向量求二面角时，必须解决一个问题：所求得的两个半平面的法向量的夹角，是等于二面角的大小，还是等于此二面角的补角的大小？这取决于两个法向量的方向.

为区分二面角两个半平面的法向量的方向，先定义一个“向内法向量”和“向外法向量”概念.

结论1：设向量m和n分别是二面角α-a-β的面α和β的法向量.若m和n都向该二面角内，或都向该二面角外，则向量夹角〈m，n〉与二面角α-a-β的平面角互补；若m和n一个向二面角内，另一个向二面角外，则〈m，n〉与二面角α-a-β的平面角相等.

证明：设P为二面角α-a-β内一点，PH和PR分别与半平面α，β垂直，垂足H∈面α，R∈面β，设过PH和PR的平面与棱a交于点Q，连接HQ，RQ，得到平面四边形PHQR，其中有两个对角是直角.因为，这里向外向内向外向内.在四边形PHQR中，∠HQR+∠P=π，即∠HQR+=π，且∠HQR+=π；又显然cos=-cos，所以，即∠P+=π.得∠HQR=，同理∠HQR=，这就证明了，若m和n都向该二面角内，或都向该二面角外，则向量夹角〈m，n〉与二面角α-a-β的平面角互补；若m和n分别是二面角α-a-β“向内”和“向外”的法向量，则〈m，n〉与二面角αa-β的平面角相等.

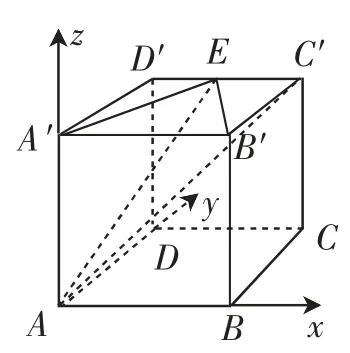
图1

例1 如图1，在棱长为1的正方体ABCD-A′B′C′D′中，E是C′D′的中点，求二面角A-B′E-A′和A-B′E-C′的大小.

解析：以AB的方向为x轴正方向，AD的方向为y轴正方向，AA′的方向为z轴正方向，建立坐标系.如图1所示，则A（0，0，0），B′（1，0，1），E，C′（1，1，1）.取平面ABCD的一个法向量n=（0，0，1），平面AB′E的法向量m=（x，y，z）由得x+z=0，由得则设θ=〈m，n〉，则cosθ=对于两补邻二面角都向外，而m对于二面角A-B′E-A′向外，对于二面角A-B′E-C′向内.

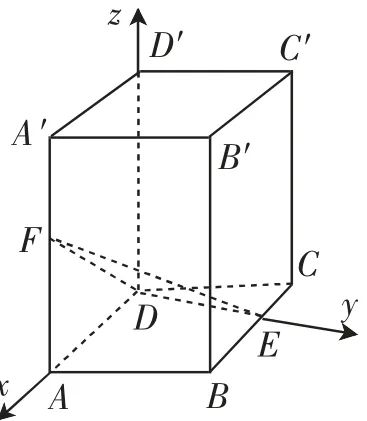
图2

例2 如图2，直四棱柱ABCD-A′B′C′D′的底面是菱形，AA′=4，AB=2，∠BAD=60°，E，F分别是BC和AA′的中点.求二面角F-ED′-C的大小.

解：如图2，以D点为原点，DA的方向为x轴的正方向，DE的方向为y轴的正方向，DD′的方向为z轴正方向，建立空间直角坐标系，则D（0，0，0），D′（0，0，4），C（-2，，0），E（0，，0），F（2，0，2），=（0，，-4），=（2，0，-2）（-2，0，0）.设面D′EC的法向量为m=（x，y，z）.由得-2x=0，由，得y-4z=0.所以m=取面D′EF的法向量n=（x1，y1，z1）.由=0，得y1-4z1=0得2x1-2z1=0.所以n=由定义知，平面D′EC的法向量m和平面D′EF的法向量n都向二面角F-ED′-C外.由结论1知，法向量夹角与二面角互补.cos〈n，m〉=

例3 四边形ABCD是正方形，E，F分别是AD和BC的中点.把△CDF沿DF折起，使得点C到点P的位置，且PF⊥BF.

（1）求二面角D-PF-C的大小；

（2）求二面角B-PC-D的大小；

（3）设G点是AD边上的点，求二面角G-PB-C为钝二面角、直二面角、锐二面角时G点的位置.

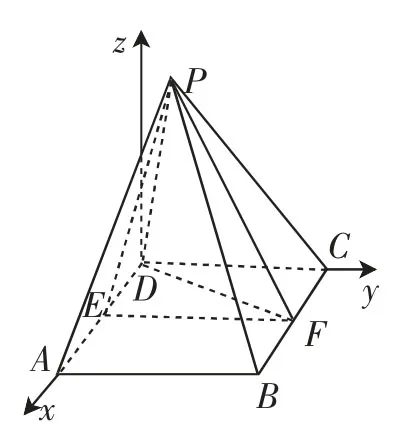
图3

解：（1）如图3，因为E，F分别为正方形ABCD的边AD，BC的中点，所以BC⊥EF.又BC⊥PF，所以BC⊥平面PEF.所以AD⊥平面PEF，则AD⊥PE.设正方形ABCD的边长为2.在Rt△PDE中，PD=2，DE=1，所以PE=.又EF=2，PF=1，所以△PEF是直角三角形，∠EPF=90°.因为平面PEF⊥平面ABCD，作PH⊥EF与EF交于H点，则PH⊥平面ABCD.求得PH=.现以D点为原点，DA，DC分别为x轴，y轴的正方向，建立空间直角坐标系，则D（0，0，0），C（0，2，0），设平面PFC的法向量为m=（x，y，z），平面PDF的法向量为n=（x1，y1，z1）.由m·得，由得0，取得一组解是.由n·得，由得取得一组解是x=-6，y=3，因此设〈m，n〉=θ，则cosθ=，所以θ=60°.由于m向二面角外，n向二面角内，由结论1知θ就等于二面角的大小.即二面角D-PF-C的大小为60°.

（2）B（2，2，0），E（1，0，0），C（0，2，0），P设平面PBC的法向量为m=（x，y，z），平面PEB的法向量为n=（x1，y1，z1）.由得2x=0，x=0，由得z=0，得m=.由得x1+2y1=0，由得，令y1=1，则x1=-2，z=0，故得到n=（2，1，0），于是两向量夹角的余弦值cos〈m，n〉=可见m向二面角外，n也向外，由结论知，二面角B-PC-D为钝角π-arccos