单点系泊系统液滑环弹簧蓄能密封圈密封性能研究

高涵宇 李佳君 杜 彬2 李林燎 孙家斌 岳前进

(1.大连理工大学海洋科学与技术学院 辽宁盘锦 124200； 2.潍柴重机股份有限公司零部件分公司 山东潍坊 261108)

液滑环作为单点系泊系统中最为关键的零部件，其设计和制造技术长期被国外垄断，价格高昂，制约我国海上油田建设的快速发展[1]。液滑环需要在旋转接头处配备多重密封装置，从而阻碍原油泄漏[2]。液滑环工作在高温高压的动态密封过程，而单一的橡胶材料无法满足高温高压的动态密封过程，因此蓄能弹簧密封圈得以出现。蓄能弹簧密封圈的主体材料选取改性聚四氟乙烯，由于改性PTFE材料耐高温、耐腐蚀、耐磨性好、润滑性好，可以应对恶劣的工作环境，因此弹簧蓄能密封圈具有优良的自密封和回弹性，可及时解决因材料磨损、应力松弛及装配偏移导致的密封失效问题，同时介质压力也会辅助提高密封性能。

目前弹簧蓄能密封圈广泛用于动态和静态密封中[3]。国际上常见成熟的密封圈产品主要包括Trelleborg的Turcon Variseal弹簧密封圈和Saint-gobain公司的OmniSeal系列蓄能弹簧密封圈等。由于技术封锁，我国对其密封性能的研究甚少。桑园[4]利用ANSYS对弹簧蓄能密封圈接触区的接触压力分布进行了研究；贾晓红等[5]提出了采用变截面圆环模拟螺旋弹簧的二维等效方法。

本文作者利用Abaqus商业软件建立蓄能弹簧密封圈的二维轴对称模型，分析了U形弹簧对系统密封性能的补偿能力，基于正交试验法对不同尺寸弹簧蓄能密封圈进行仿真模拟，得到各参数对密封区域接触压力的影响，并获得了密封性能最优的模型尺寸参数。

1 弹簧蓄能密封圈有限元分析计算

1.1 几何模型

图1为滑环结构图，液滑环由内环和外环组成，内环固定不动，驱动臂连接吊耳带动外环旋转，液体从进油口输入并在环形腔道中流动，密封圈结构如图2所示，尺寸选择φ1 000 mm×18 mm×10.6 mm,唇口直径0.6 mm、唇厚1.5 mm、唇长11.3 mm、被压环厚度6.7 mm。将弹簧蓄能密封圈简化为平面二维轴对称模型进行分析。

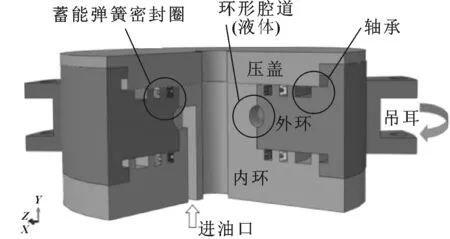
图1 液滑环结构Fig 1 Structure of liquid swivel

图2 蓄能弹簧密封圈Fig 2 spring energized seal ring

1.2 材料模型

滑环的内外环等效成解析刚体进行分析，弹簧采用不锈钢，弹性模量E=210 GPa、泊松比ν=0.3。根据法国圣戈班密封公司[6]提供的Fluoroloy®A49材料：改性PTFE夹套材料弹性模量E=800 MPa，泊松比ν=0.46。为方便有限元计算能够快速有效，现做以下假设：(1)忽略原油温度对密封圈的影响；(2)聚四氟乙烯假定为弹塑性材料；(3)滑环的内外环弹性模量远大于密封圈材料，选用解析刚体分析。

1.3 网格划分

图3所示是模型的网格划分情况,密封圈夹套选用CAX4IH单元，共3 254个。杂交非协调单元。杂交单元主要适用于不可压缩材料，在单元变形比较小时，非协调单元能克服剪切自锁，得到精确的位移和应力结果；单元形状皆为四边形为主，自由扫掠，采用进阶算法，在合适的地方使用映射网络[7]。弹簧是主要受力部位，为方便计算，将弹簧与密封圈建成一体，分区赋予材料属性，选用CAX4R单元，减缩积分，共266个。

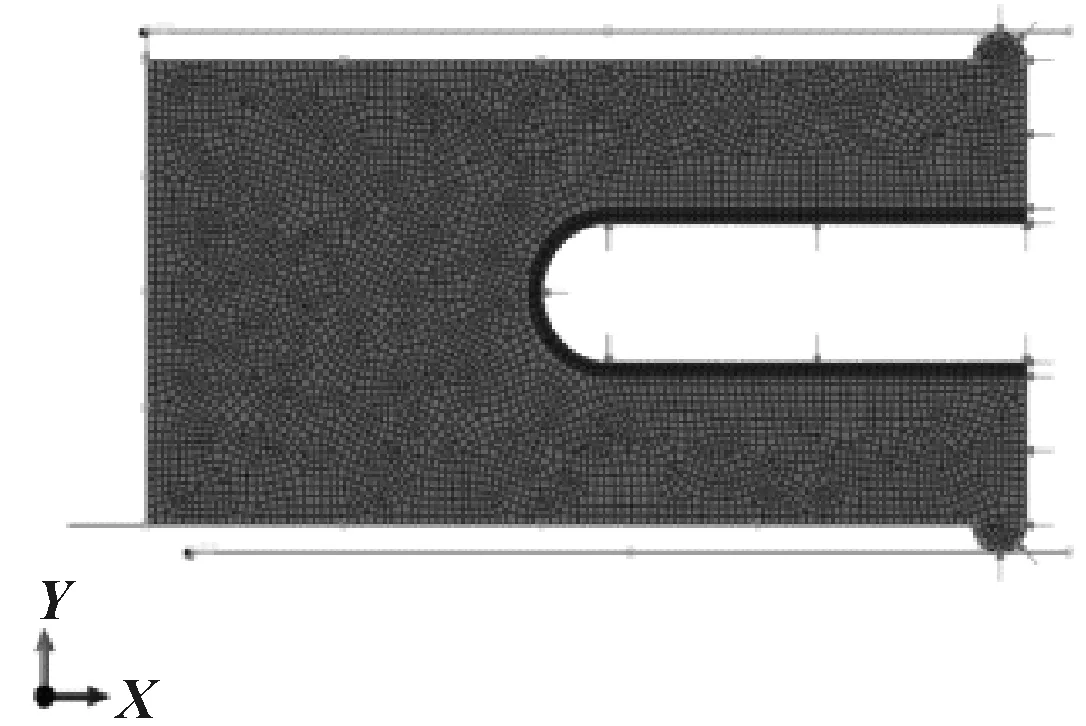
图3 网格划分及载荷分布情况Fig 3 Meshing and loading on the seal ring

1.4 接触设置

文中接触算法采用罚函数法

Πp=1/2pTEpp

(1)

式中：Ep是惩罚因子；p为嵌入深度，是结点位移U的函数。罚模型允许黏性接触面之间有小量的相对滑动，便于求解非线性问题，摩擦因数选取0.2。如图4所示，设置滑环上壁与密封圈上端为面面接触，滑环上壁为“主面”，密封圈上端接触面为“从面”。Abaqus里选择刚度较大、网格划分较疏的接触面为“主面”；同理，密封圈下端接触面为“从面”，滑环下壁为“主面”；滑环上壁左侧面为“主面”，密封圈根部接触面为“从面”，法向接触属性选择“硬接触”，防止面面之间发生穿透。

图4 密封圈与密封槽装配方式Fig 4 Assembly of sealing ring and sealing groove

1.5 边界条件与加载

对滑环下壁全约束，给上壁y轴负方向初始位移0.2 mm，蓄能弹簧密封圈没有边界条件约束，共设有2个分析步，分别为：第一步，预压缩，橡胶圈在密封沟槽中的实际状态是压紧的，建立所有接触对；第二步，模拟实际工作状态通压5 MPa，U形密封圈开口方向正对密封液体，是主要的承压部位。

1.6 密封性能判定条件

滑环的密封形式属于弹性体自紧密封，保证密封的必要条件是密封处最大接触应力大于介质压力[8-9]。密封形式属于动密封，考虑密封圈表面摩擦力对密封性能的影响，引入接触面处的线接触压力：

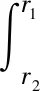
(2)

式中:F1为弹簧蓄能密封圈截面径向线接触压力，N；r1、r2分别为初始接触点及最终接触点的径向坐标值，mm；σr为上唇口接触应力，MPa。

为了便于简化运算过程，进行比较，文中模拟默认密封圈接触区域的位置相同，即直径相同，只比较径向方向上的线接触应力大小。

2 结果及分析

2.1 上下唇口接触应力分布

如图5所示，显然密封圈截面的对称性起到了作用，上下唇的应力值相差较小，整体趋势相同，故此后的模型中仅选取上唇口应力分布进行分析。

图5 上下唇口应力分布对比Fig 5 Stress distribution of upper and lower lips

2.2 弹簧形式简化

弹簧为密封夹套提供恢复力，在预压缩或通压时，弹簧刚度大，恢复原有形状的能力强于PTFE夹套，可以保证密封性能。弹簧厚度选取2 mm，如图6所示，有弹簧的密封圈密封性能明显更优，弹簧提供了额外的回弹力;无弹簧时11～13 mm处出现小波峰，上唇中段发生大变形与密封沟槽接触，液滑环属于旋转机构，接触产生的摩擦会使密封圈磨损，减少使用寿命并影响密封效果。嵌入弹簧以增加刚度，即可解决此问题。

图6 有无弹簧的密封圈应力分布Fig 6 Stress distribution of sealing ring with spring or not

2.3 结构优化设计

一种性能优越的密封圈，需要同时拥有较低的摩擦力(由线接触压力产生的径向力)和较高的最大接触压力，故采用正交实验法分析密封圈的结构参数对上述两指标的影响[10-12]。唇口直径、唇长、唇厚、被压环厚度为主要参考因素，记作A、B、C、D，对4个因素进行正交试验，每个因素均取5个水平，因素水平表与前期控制变量法相同。密封圈关键参数选取如表1所示，选择L25(56)的正交表。

表1 密封圈简化模型主要参数水平

将线接触压力与最大接触压力作为评价密封圈密封性能的2个指标。根据最新的参数组合绘制出相应的模型如图7所示，弹簧厚度统一取2 mm。

图7 密封圈具体参数Fig 7 Specific parameters of sealing ring

图8和图9所示为唇口直径和唇厚对线接触压力和峰值接触压力的影响,随着唇口直径增大，峰值接触压力和线接触压力均是先增大后减小。当唇口直径为2.0 mm时二者的差值出现最大值。唇厚对接触压力的影响规律与唇口直径相似，在唇厚为2.5 mm处线接触压力与峰值接触压力的差值最大，因为线接触压力由积分得到，所以对变量的敏感程度较小。

图8 唇口直径对线接触压力和峰值接触压力的影响Fig 8 Effect of lip diameter on line-contact and peak contact pressure

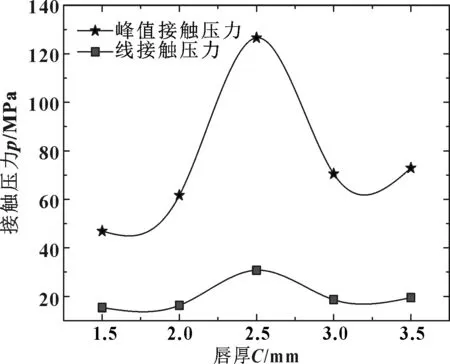
图9 唇厚对线接触压力和峰值接触压力的影响Fig 9 Effect of the thickness of lip on line-contact and peak contact pressure

图10和图11所示为唇长与被压环厚度对线接触压力和峰值接触压力的影响规律，可以看出密封接触压力远远大于液体压力5 MPa，保证密封性能。如图10所示，唇长增加，线接触压力和峰值接触压力增大，唇长为11 mm时上升最快，可能是唇长选型的临界值。从图11可以看出，被压环厚度造成的影响相反，在被压环厚小于6 mm时下降最快，在6～9 mm范围内接触压力与峰值接触压力下降平缓，影响很小。

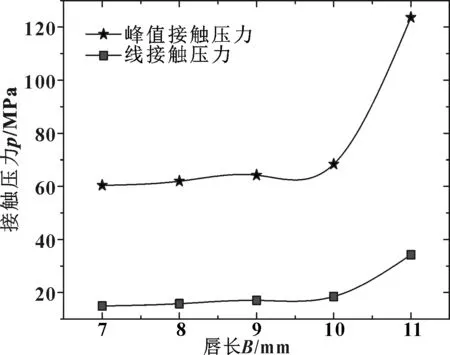
图10 唇长对线接触压力和峰值接触压力的影响Fig 10 Effect of the length of line-contact and peak contact pressure

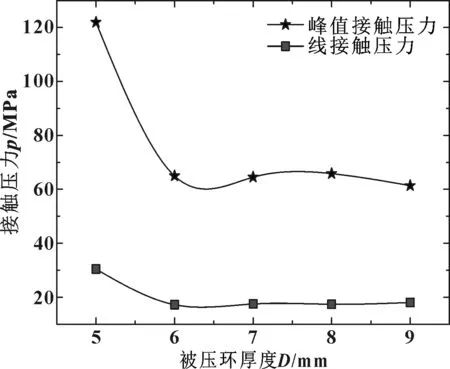
图11 被压环厚度对线接触压力和峰值接触压力的影响Fig 11 Effect of the thickness of compression ring on line-contact and peak contact pressure

为了确定各个参数对密封性能的影响程度，引入极差Rj，各因素的主次顺序通过各自的极差Rj的大小进行判定

Rj=max(kj)-min(kj)

(3)

式中：Rj表示在取值范围内该因素的试验指标变化的幅度；kj为某因素某水平下的试验指标均值。

极差越大，表示该因素的水平变化对试验指标峰值接触应力的影响越大，该因素越重要。

文中极差Rj计算结果如表2、表3所示。结合表2对k值的综合观察，k1和k5最大，因为峰值接触应力越大密封性能越好，选取A1C5为优水平。结合表3以线接触压力为指标，数值越小密封圈磨损越小，综合考虑A1C1为优水平。结合表2以峰值接触压力为指标，选取B2D2为优水平；结合表3,以线接触压力为指标，选取B5D5为优水平。

通过比较各R值的大小，以峰值接触压力为指标可知唇口直径的R最大，所以各因素对试验指标影响的主次顺序依次是C、A、B、D。即唇厚影响最大，其次是唇口直径和唇长，而被压环厚度的影响较小。以线接触压力为指标，则唇长影响最大，其次是唇口直径和唇厚，被压环厚度的影响最小。

表2峰值接触应力指标下的分析结果

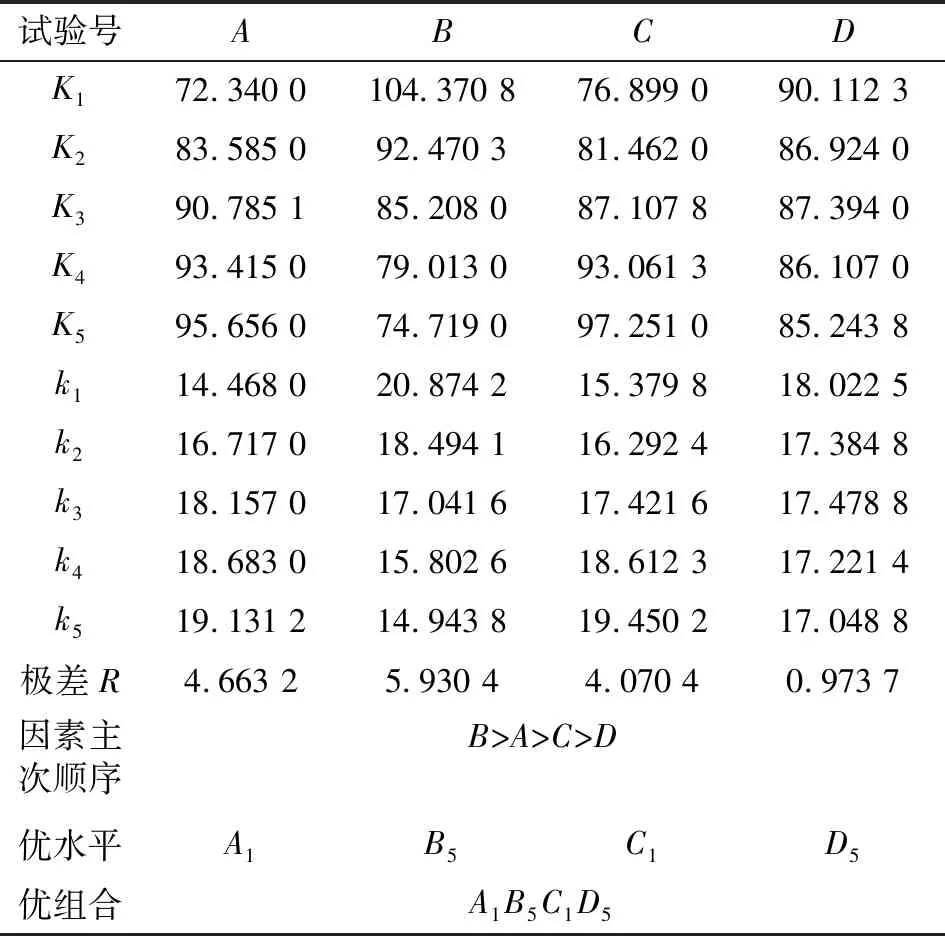
表3 线接触压力指标下的分析结果

表4中给出了2个指标下各因素的极差在总极差中的比重，对比可知，对B因素而言，线接触压力指标下的极差占比大，选择该指标下的最优水平作为优化模型的最优值，即选择唇长7 mm。同理可知，最优模型唇厚为3.5 mm。对于A和D2个因素，其占比相近，各自进行分析。对于A因素，不论是哪种指标下，都是唇口直径1.2 mm为最优值，而对D因素而言，考虑正交试验中被压环厚度的变化趋势，被压环厚度为5 mm时2个指标差值最大，选择被压环厚度5 mm作为最优值。结合2种指标下的极差分析，观察极差占比，对于峰值接触压力，唇厚的值占比高达0.483 5，接近50%，足以体现该参数重要性，故C排在B前面，而A与D排序位置不变，重要度排序由大到小依次为C、A、B、D。

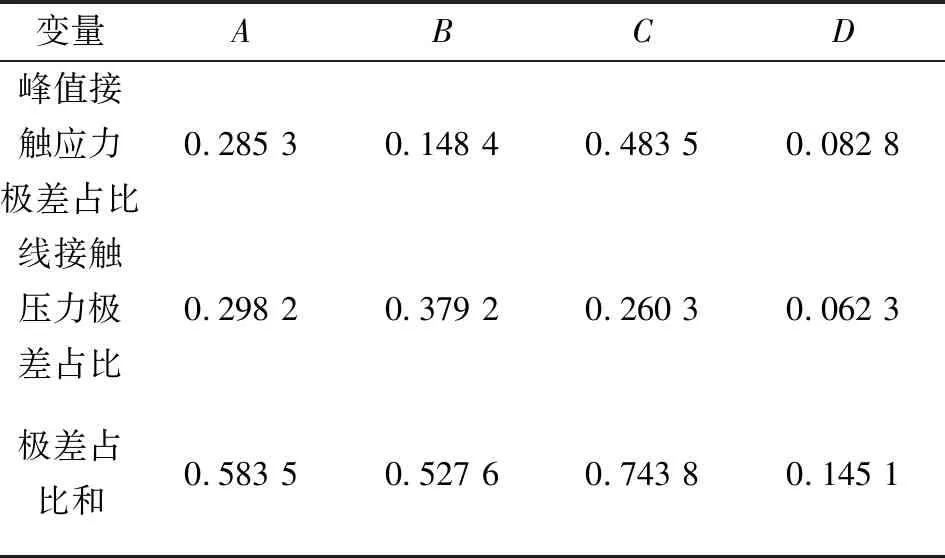
表4 极差分析

3 结论

(1)对蓄能弹簧密封圈模型进行简化，将密封圈材料简化为弹性体，验证了弹簧对于密封接触压力的补偿能力。

(2)在满足密封性能的前提下对正交实验结果进行极差分析，得到影响密封圈峰值接触压力的各因素主次顺序依次为唇厚、唇口直径、唇长、被压环厚；影响密封圈线性接触压力的各因素主次顺序依次为唇长、唇口直径、唇厚、被压环厚。综合二者得到最后的各因素主次顺序依次为唇厚、唇口直径、唇长、被压环厚。

(3)在文中所用模型参数下，蓄能弹簧密封圈的最优结构参数值：唇口直径1.2 mm，唇长7 mm，唇厚3.5 mm，被压环厚度5 mm。