构建模型，让边角关系深度呈现*——2019年南通中考第17题的解法探究与思考

江苏省海门市东洲国际学校 张浩杰

纵观南通中考近三年的填空题，都有一道涉及反比例函数图像与几何图形完美结合的中档题，意在挖掘边和角之间的一种内在联系，重在考查学生从形的角度突破，从数的角度解决的基本技能、基本路径，旨在教师的教学过程中，深层次理解图形的“边角关系”.

一、原题呈现

（2019年南通中考）如图1，过点C（3，4）的直线y=2x+b交x轴于点A，∠ABC=90°，AB=CB，曲线y=（x＞0）过点B，将点A沿y轴的正方向平移a个单位长度恰好落在该曲线上，则a的值为______.

图1

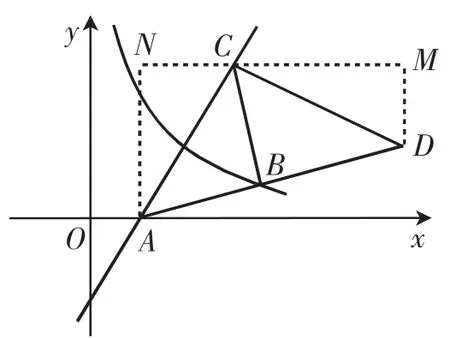
图2

二、方法思考

从已知条件中可以发现△ABC是等腰直角三角形，可知特殊角、边的关系、边角关系及延伸而出的其他相关性质.结合问题，解决的关键点在于求出k的值，可以从数或形的角度攻克.

1.构造“K”型（全等三角形）

（1）如图2，以点C为直角顶点构造等腰直角三角形ACD，分别过点C作x轴的平行线，过A、D两点作y轴的平行线，交于N、M两点，可以发现由已知可求得直线AC∶y=2x-2、点A（1，0），则CM=AN=4，DM=CN=2，则点D（7，2）.由CB⊥AD，得B是AD的中点，则点B（4，1），则抛物线为，可求得a=4.

（2）如图3，过点B作BD⊥AC，垂足为点D，则D为AC的中点，则点D（2，2）.同（1）构造“K”型，则AN=DM=2，DN=BM=1，则点B（4，1），则抛物线为y=，可求得a=4.

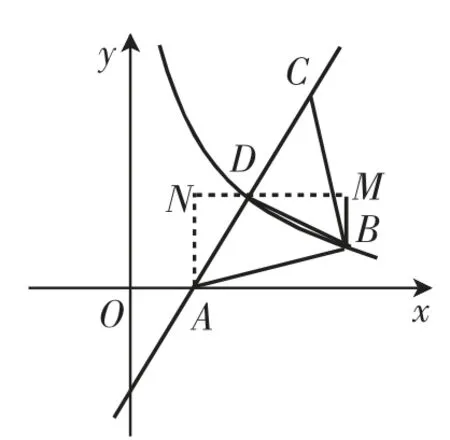
图3

图4

2.构造一线三等角模型

如图5，分别过点C、B作x轴的垂线，垂足分别为点P、M，分别以PC、BM为直角边在PC左侧、BM右侧作等腰直角△PCD、△BMN.则.又AD=2，CD=，则BM=MN=1，AN=4，则点B（4，1），则抛物线为，可求得a=4.

图5

图6

3.构造两角和为45°模型

如图6，构造矩形ANMD.由∠CAB=45°，得∠NAC+∠BAD=45°.可求得tan∠NAC=.若能求出tan∠BAD，则同样可求出点B的坐标.如何求tan∠BAD？可以通过以下探究过程实现.

如图7，矩形ABCD中，∠EAF=45°，且满足△AEF是等腰直角三角形，则，可求得.根据以上方法在图6中可求得，则点B（4，1），则抛物线为y=，可求得a=4.

三、解后再思

1.45°角的联想

（1）抓住45°角，构造“K”型或一线三等角，利用“边角”关系，形成全等三角形或相似三角形，为形向数转化打下基础.在“K”型构造上，需找直角，可利用现有的，如方法1（3）；可以借助已知点作为直角顶点，如方法1（1）；也可利用图形的性质去构造，如方法1（2）.对于一线三等角而言，主要还是相似模型的构建，真正让边角关系无处不在.

（2）从一个角为45°转化为两角和为45°，通过构造矩形，可推导出“45°+”的正切公式，其本质涉及高中知识：两角和的正切公式tan（α+β）=对于学有余力的学生，可以引导他们进一步探究推导其他一些性质：如当α=β时；如α+β=45°，且知其中一角的正切值，则可求另一角的正切值（三者可知二求一）.利用这些探究，可将较为复杂的边角之间的比例关系轻松破解.

图7

图8

2.三角形边角关系之间的变化，形成变式

路径（1），直角三角形中锐角的度数发生变化，如：把“∠ABC=90°，AB=CB”改为“直角△ABC中，∠CAB=30°或60°”，其他不变，以上解决问题的方法同样适用，变化的是构造“K”型中，由全等三角形转为相似三角形.

路径（2），三角形形状的改变，“∠ABC=90°，AB=CB”改为“等边△ABC”，改编如下：

如图8，过点C（3，4）的直线y=2x+b交x轴于点A，△ABC是等边三角形，曲线y=（x＞0）过点B，将点A沿y轴的正方向平移a个单位长度恰好落在该曲线上，则a的值为______.

路径（3），边之间的数量关系发生变化，如：“∠ABC=90°，AB=CB”改为“Rt△ABC，且”，即：

如图1，过点C（3，4）的直线y=2x+b交x轴于点A，△ABC是直角三角形，且，曲线y=（x＞0）过点B，将点A沿y轴的正方向平移a个单位长度恰好落在该曲线上，则a的值为______.

3.解题教学走向深度

我们知道，学习数学的过程与数学解题紧密相关，学生数学能力的提升在于解题的质量而非数量，解题质量的提升路在何方？教会学生有想法，教会学生有对比，教会学生有反思，则是重中之重.本题的研究看似用好45°角，其本质可以延伸于角的存在性问题的思考策略，举一反三，从而达到殊途同归的目的.解决本题的思路有多种，从基本思路到思路优化再到高位思考，在这样的过程中让学生体验到方法的融会贯通，达到触类旁通的功效，尤其是推导“45°+”正切公式的历程，激发学生对于高中知识探究的欲望，能够有效提升学生的数学能力，因此解题教学的着力点要落在学法指导上.当然，解题教学的发展点要落在问题演变上，从一题走向一类，从而让学生从变化中发现不变的结构，进一步训练学生的有效提炼，真正实现学生从学解题达到会解题，使解题教学走向深度教学.