四边形中的变式探究题探析

江苏省南京外国语学校 陶维维

新课程标准指出，数学课程不仅要使学生掌握必备的基础知识与技能，而且要培养学生的创新意识与实际操作能力，发展学生的情感、意志，形成正确的人生观、世界观和价值观.四边形的变式探究问题，能使学生在自主探究、实际操作与合作交流中，收获更多的数学活动经验，它包括两种类型的探究：一是探索在不变条件下，当动点位置不同时能否得到相同的结论；二是探究由特殊情形得到的结论能否推广到一般情况，它既考查了学生对四边形性质与判定的理解与掌握，也考查了学生的创新精神与实践能力.

一、平行四边形变式探究题

平行四边形的性质包括：对边平行且相等，对角相等，邻角互补，对角线互相平分.它的判定方法有五种，用边来判定的方法有三种，用角来判定、用对角线判定的各一种方法.平行四边形是中心对称图形，所以，相同条件的不同图形可能得到同一结论.

例1在▱ABCD中，对角线AC、BD交于点O，将过点A的直线l绕点A旋转，交射线CD于点E，BF⊥l于点F，DG⊥l于点G，连接OF、OG.

（1）如图1，当点E与点C重合时，请直接写出线段OF、OG的数量关系；

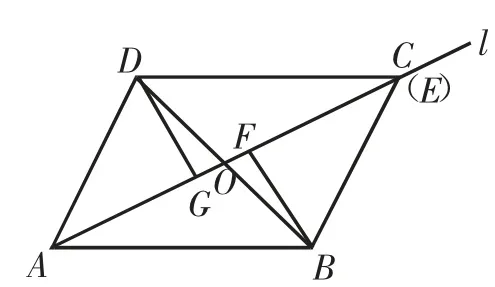
图1

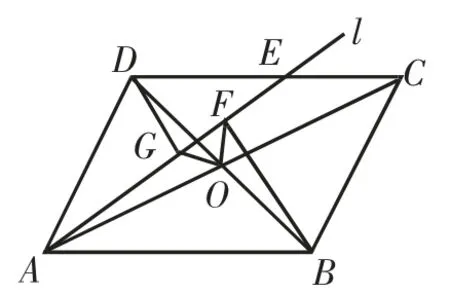
图2

（2）如图2，当点E在线段CD上时，OF与OG有什么数量关系？请证明你的结论.

（3）如图3，当点E在线段CD的延长线上时，上述结论是否仍成立？请说明理由.

解析：（1）OF=OG，理由如下.

由四边形ABCD是平行四边形，得OB=OD.

由BF⊥l于点F，DG⊥l于点G，得∠BFO=∠DGO=90°.

（2）OF=OG，理由如下.

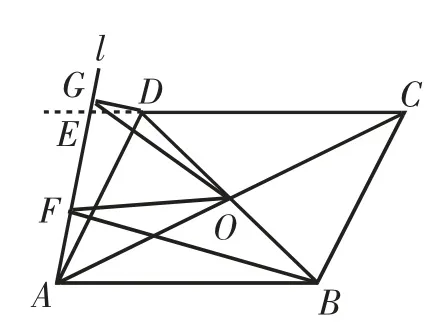
图3

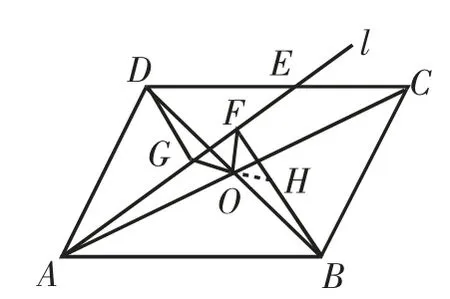
图4

延长GO交BF于点H，如图4所示.

由BF⊥l于点F，DG⊥l于点G，得BF∥DG，则∠ODG=∠OBH.

（3）当点E在线段CD的延长线上时，上述结论仍成立，理由如下.

延长GO、FB交于点H，如图5 所示.

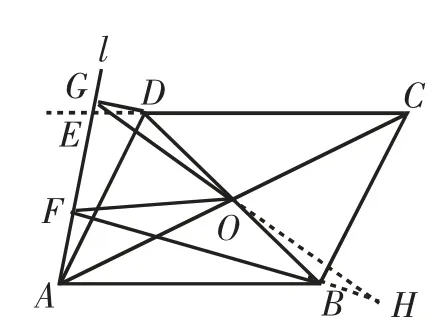
图5

由四边形ABCD是平行四边形，得OB=OD，

由BF⊥l于点F，DG⊥l于点G，得BF∥DG，则∠DGO=∠BHO.

评注：本题在解答过程中主要应用了全等三角形、直角三角形斜边中线的性质、平行四边形的性质等，在解答第（2）问和第（3）问时，解题思路是相同的，都是延长一边构造直角三角形.

二、菱形变式探究题

菱形不仅具有平行四边形的一切性质，而且有自己特殊的性质，即四边相等，对角线互相垂直平分，每条对角线平分一组对角.它的判定方法有三种，用边来判定的两种，用对角线来判定的一种.因为它既是轴对称图形也是中心对称图形，所以当一个角的顶点与菱形的顶点或中心重合时，在旋转过程中始终有全等三角形.

例2已知四边形ABCD是菱形，AB=4，∠ABC=60°，有一足够大的含60°角的直角三角尺的60°角的顶点与菱形ABCD的顶点A重合，两边分别与CB、DC相交于点E、F，且∠EAF=60°.

（1）如图6，当点E是线段CB的中点时，请直接判断△AEF的形状是______.

图6

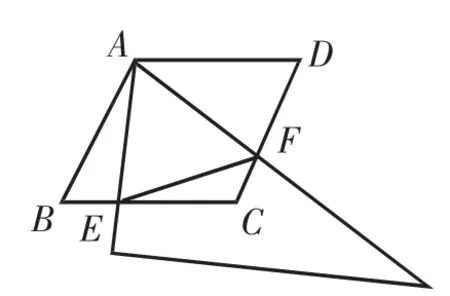
图7

（2）如图7，当点E是线段CB上任意一点时（点E不与点B、C重合），求证：BE=CF.

（3）如图8，当点E在线段CB的延长线上，且∠EAB=15°时，求点F到BC的距离.

解析：（1）△AEF是等边三角形，理由如下.

连接AC.

由四边形ABCD是菱形，得AB=BC=AD，∠B=∠D.

由∠ABC=60°，得∠BAD=120°，△ABC是等边三角形，则AC=AB.

由点E是线段CB的中点，得AE⊥BC，则∠BAE=30°.又∠EAF=60°，则∠DAF=120°-30°-60°=30°=∠BAE.

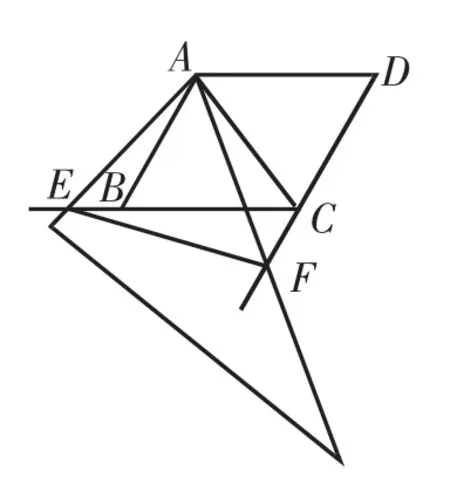
图8

（2）连接AC.

同（1）得△ABC是等边三角形，则∠BAC=∠ACB=60°，AB=AC.

又∠EAF=60°，则∠BAE=∠CAF.

由∠BCD=∠BAD=120°，得∠ACF=60°=∠B.

（3）同（1）得：△ABC和△ACD是等边三角形，则AB=AC，∠BAC=∠ACB=∠ACD=60°，则∠ACF=120°.

由∠ABC=60°，得∠ABE=120°=∠ACF.

由∠BAC=60°，∠EAF=60°，得∠BAE=∠CAF.

由∠EAB=15°，∠ABC=∠AEB+∠EAB=60°，得∠AEB=45°，则∠CEF=∠AEF-∠AEB=15°.

作FH⊥BC于点H，在△CEF内部作∠EFG=∠CEF=15°，如图9所示.

由∠FCH=∠ACF-∠ACB=60°，得∠CFH=30°，则CF=2CH，FH=

由BC=AB=4，得CE=BC+BE=4+2x，则EH=4+x=x+3x，解得x=，则FH=，即点F到BC的距离为

评注：其实在∠EAF绕点A旋转的过程中，始终有不变的结论，如：BE=CF，△AEF是等边三角形，其他结论都是在这些结论的前提下进一步延伸的.

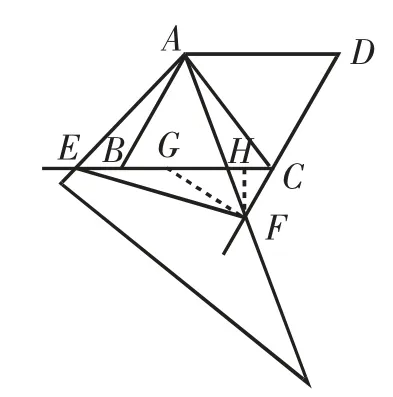
图9

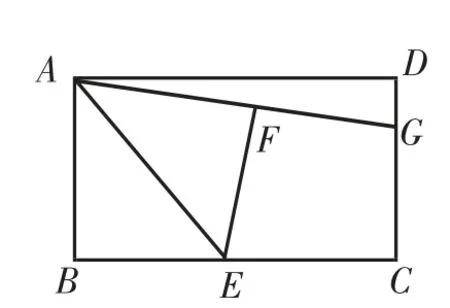
图10

三、矩形的变式探究

矩形不仅具有平行四边形的一切性质，而且有特殊的性质，即四个角都是直角，对角线相等.它的判定方法有三种，用角判定的两种，用对角线判定的一种.因为矩形既是轴对称图形也是中心对称图形，所以在矩形内探究的结论可以推广到一般的平行四边形中.

例3（1）【操作发现】如图10，在矩形ABCD中，E是BC的中点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G.猜想线段GF与GC的数量关系是_______.

（2）【类比探究】如图11，将（1）中的矩形ABCD改为平行四边形，其他条件不变，（1）中的结论是否仍然成立？请说明理由.

图11

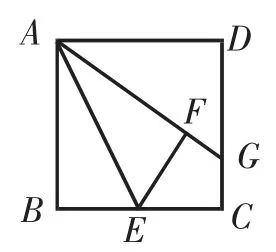
图12

（3）【应用】如图12，将（1）中的矩形ABCD改为正方形，边长AB=4，其他条件不变，求线段GC的长.

解析：（1）GF=GC，理由如下.

连接EG.

由E是BC的中点，得BE=CE.

由将△ABE沿AE折叠后得到△AFE，得BE=EF，则EF=EC.又EG=EG，∠C=∠EFG=90°，则△ECG△EFG（HL），则FG=CG.

（2）（1）中的结论仍然成立.理由如下.

连接FC.由E是BC的中点，得BE=CE.

由将△ABE沿AE折叠后得到△AFE，得BE=EF，∠B=∠AFE，则EF=EC，则∠EFC=∠ECF.

由矩形ABCD，得∠B=∠D.

由∠ECD=180°-∠D，∠EFG=180°-∠AFE=180°-∠B=180°-∠D，得∠ECD=∠EFG，则∠GFC=∠GFE-∠EFC=∠ECG-∠ECF=∠GCF，则∠GFC=∠GCF，则FG=CG.

（3）设GF=GC=x，则AG=4+x，DG=4-x.

在Rt△ADG中，（4+x）2=（4-x）2+42，解得x=1，即CG=1.

评注：本题将矩形中得到的“FG=CG”推广到一般平行四边形中，然后在正方形中应用，反映了变式探究的一般过程，即实验发现—类比探究—推广应用.

变式探究题在变化的图形中有不变的结论，或者随图形的变化结论做相应的改变，在解题中，锻练了学生的观察能力、逻辑思维能力，对问题追根求源的探究欲望，提升了学生对数学现象本质的认识，体会如何在变化过程中把握不变.