深度探究，挖掘内涵——对2019年杭州市中考数学第16题的思考及探究

浙江省杭州钱塘新区教师教育学院 童永芳

一、原题呈现

如图1，把某矩形纸片ABCD沿EF、GH折叠（点E、H在AD边上，点F、G在BC边上），使点B和C落在AD边上同一点P处，点A的对称点为点A′，点D的对称点为点D′.若∠FPG=90°，△A′EP的面积为4，△D′PH的面积为1，则矩形ABCD的面积等于______.

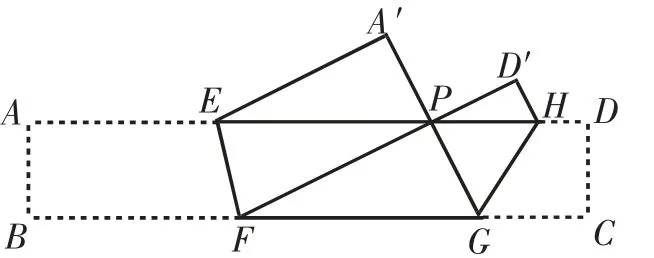
图1

二、试题分析解答

矩形折叠问题主要考查图形变化中的轴对称.了解轴对称的概念，探索轴对称图形的基本性质：成轴对称的两个图形全等，对应点的连线被对称轴垂直平分，是教学中的重点.显然，本题承载了课标对轴对称的考查要求.

问题中的条件有：①矩形ABCD沿EF、GH折叠（点E、H在AD边上，点F、G在BC边上），点B和C落在AD边上同一点P处；②∠FPG=90°；③△A′EP的面积为4，△D′PH的面积为1.结论是求矩形ABCD的面积.

由∠FPG=90°，∠A′=∠A=90°，∠D′=∠D=90°，得PF∥A′E，PG∥D′H，则△A′EP与△D′PH相似.又△A′EP的面积为4，△D′PH的面积为1，则两三角形的相似比为2∶1.由折叠可得PA′=AB=CD=PD′，从而求出△A′EP的每一条边和△D′PH的每一条边，再根据折叠知道AE=A′E=4，HD=HD′=1.最后由AB=2，AD=，得矩形ABCD的面积为

三、深度探究

解出答案后，我们去细细分析题目中每一个条件和结论，意外收获一些有趣的结论.

1.针对条件①点B和C落在AD边上同一点P处

折叠矩形一次，将矩形纸片ABCD沿EF折叠（点E在AD边上，点F在BC边上），使得点B落在AD边上，这只要AD≥AB即可，日常生活中，我们常常利用图2的方式从普通的A4纸中折出一个正方形.但是，此时按要求将点C也折起，落在同一点P处，显然做不到.

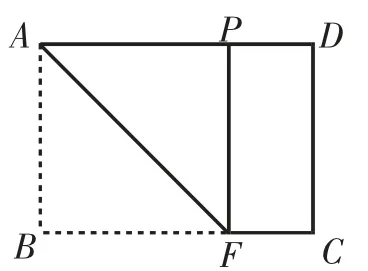
图2

利用刚才的结论，点B落在AD上需要AD≥AB，同样，点C 落在AD 上需要AD≥CD.显然，若要点B和C落在AD边上同一点P处，则AD≥2AB，即BC与AB之比大于或等于2.如图3所示.

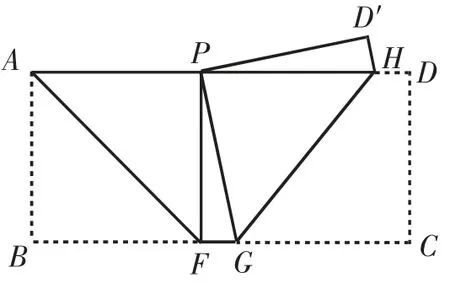
图3

2.针对条件②∠FPG=90°

折叠矩形两次，矩形纸片ABCD沿EF、GH折叠（点E、H在AD边上，点F、G在BC边上），点B和C落在AD边上同一点P处，当AD＞2AB时，我们得到新的研究对象△PFG，对于三角形，我们研究边和角及它们的关系，常见等腰三角形和直角三角形.我们先来看是否可以是等腰三角形.

（1）△PFG是等腰三角形.

显然，当点P位于AD的中点处时，PF=FG.

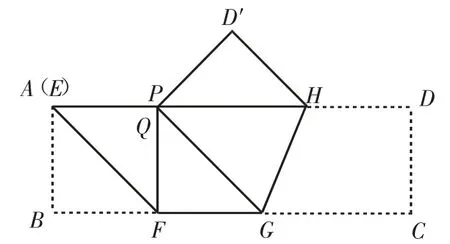
图4

如图4，在AD上截取AQ=AB，当点P与Q重合时，△PFG为直角三角形，此时若FG=FP，△PFG就是以F为顶角顶点的等腰三角形，此时GC=PG=FG，BC与AB之比为+2，是最小的.当然，在这个比值下，由对称性可得当点P在AD的中点右侧时也存在以点G为顶角顶点的等腰三角形.

在刚才的探究过程中，如图3、4，都存在以点F（G）为直角顶点的直角三角形.那∠FPG会等于90°吗？

（2）△PFG是直角三角形.

在点P移动的过程中，我们发现∠FPG先变大，再变小，当点P位于AD的中点处时∠FPG最大，而此时PF=PG，即在这个时刻，若∠FPG等于90°会满足要求.缩短AB的长，∠FPG会变大，成为钝角，即点P在AD的中点左、右两个时刻会有直角的情况存在.所以说在PF=PG，∠FPG=90°时（如图5），BC与AB的比值最小，其值为+2.而当BC与AB的比值大于+2时，如图6，∠FPG=90°.同理，根据对称性可知，点P在AD的中点右侧时也存在∠FPG=90°的情况.

图5

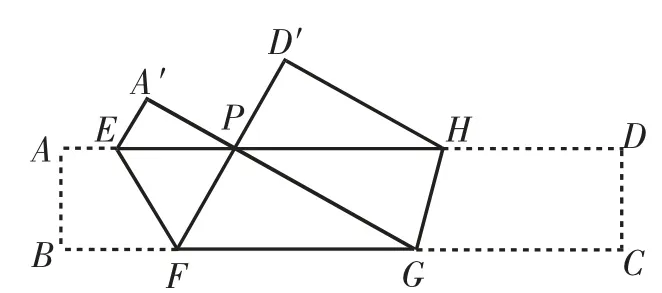
图6

继续研究∠FPG=90°的情况.

图6中，连接BE、BP、CH、CP，易得四边形EBFP、PGCH为菱形，根据菱形对角线平分一组对角，易得∠BPC等于135°.换一个角度思考问题，如图7，固定BC，若∠BPC 等 于135°，则点P在圆心角为90°的四分之一圆弧上，经过点P作出矩形ABCD都满足∠FPG=90°.

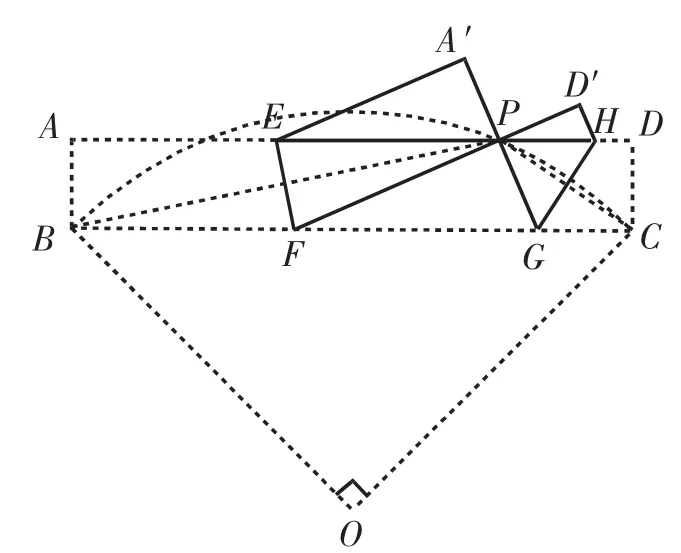
图7

如图8，当点P位于弧BC的中点处时，AB最大，连接OP交BC于点I.设PI=AB=1，OB=r，根据，得与之前计算的结果吻合.

3.针对条件③△A′EP的面积为4，△D′PH的面积为1

另外，在图1中若连接A′D′，则由△A′EP的面积为4，△D′PH的面积为1，可得△PA′D′的面积为2，则很快求得PA′=PD′=2.其原理如图9，在△ABC中，点D在BC上，DE∥AC，DF∥AB，因为，所以，所以

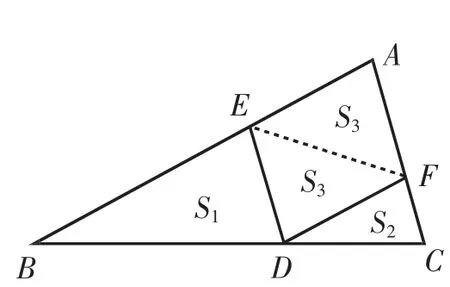
图9

图10

四、大胆猜想

1.有关∠FPG的度数

在探究中，我们发现点P从点A到点D的运动过程中，∠FPG先变大，再变小，当点P位于AD的中点处时∠FPG最大.既然∠FPG的度数随点P运动而改变，这符合函数的概念，如果设AE的长为自变量x，∠FPG的大小为因变量y，那么y关于x是怎样的函数？是我们熟系的函数类型吗？

2.有关△PFG

对△PFG的形状进行探究，主要研究△PFG的边和角的大小及关系，关于△PFG的周长，其值即为边BC的长，是问题的前提条件BC与AB的比值中的信息，那么△PFG的面积的值关于线段AE的长会是什么函数关系？同样，我们以BC=5、AB=1（BC与AB之比大于+2）为例，作出图像，观察图像（如图11），是二次函数吗？无法判断.

事实上，我们设AE的长为自变量x，△FPG的面积为因变量y，求出y 关于x 的函数，其表达式为y=，作出图像，如图12中的虚线，显然不是二次函数.

图11

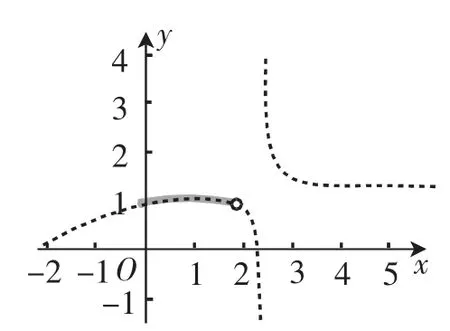
图12

五、相关结论

探究把某矩形纸片ABCD沿EF、GH折叠（点E、H在AD边上，点F、G在BC边上）问题，我们得到一些有趣的结论：

①若要点B和C落在AD边上同一点P处，则BC与AB之比大于或等于2.

②当点P位于AD的中点处时，△PFG是以点P为顶角顶点的等腰三角形；当BC与AB之比大于或等于时，△PFG可以是以点F（G）为顶角顶点的等腰三角形.

③当点P在距离点A或点D一个AB的长度时，△PFG是以点F（G）为直角顶点的直角三角形；若要∠FPG=90°，则BC与AB之比大于或等于

我们猜想：①∠FPG的度数关于AE的长可能是二次函数（有待读者验证）；

②△PFG的面积关于AE的长也可能是二次函数（结果不是）.

六、结语

中考试题凝聚了命题者的心血，其内涵丰富.在解题或解题教学中若仅仅解出答案就停止脚步，犹如入宝山而空返，十分可惜.日常教学中，教师若能引导学生对优秀的中考试题进行深度探究，并对问题提出新的猜想，提高学生学习数学的兴趣，激发学生热爱探究的精神，培养学生勇于创新的意识，最大程度发挥中考试题的教育教学功能.