三角形中的一条线、两个模型、三个结论

江苏省南通田家炳中学 潘丹丹

三角形是人教版八年级上册第十一章内容，如何研究与三角形相关的角是研究的重点与难点，通过对与三角形有关内容的分析与认识，笔者对如何求与三角形相关的角及与三角形相关的角的一些题型做了适当的认识与总结，如有不当之处，敬请批评指正.

一、三角形中的一条线——内角和定理或外角结论

与三角形有关的角包括内角和外角，如何去求相关角呢？笔者认为，牢牢抓住内角和定理或者外角结论，在求与三角形相关的角时，首先确定所研究的角是什么角，抓住三角形的内角和定理（三角形三个内角和等于180°）这条线，或者抓住外角结论（三角形的外角等于与它不相邻的两个内角的和）这条线.

基于三角形求角中一条线的思路认识，可进一步得出以下两个模型及对三个结论的认识.

二、两个模型——飞镖模型和8字模型

1.8字模型

如图1，试探究∠A、∠B、∠C、∠D的关系.

结论：∠A+∠B=∠C+∠D.

通过对三角形中研究角时一条线的认识，可知应紧抓三角形的内角和定理.证明如下：

证明：在△ABE中，∠A+∠B+∠AEB=180°，所以∠A+∠B=180°-∠AEB.

在△CDE中，∠C+∠D+∠CED=180°，所以∠C+∠D=180°-∠CED.

又因为∠AEB=∠CED，所以∠A+∠B=∠C+∠D.

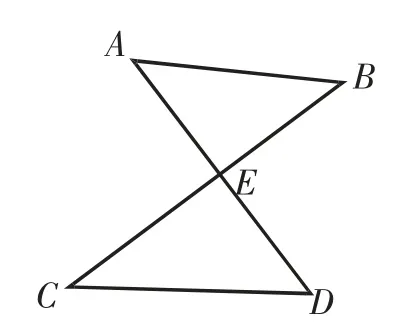
图1

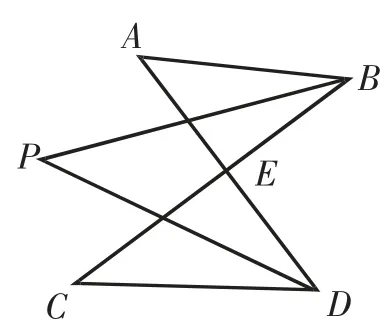
图2

建立在8字模型的基础上，将8字模型与角平分线结合，有如下问题探究：

如图2，BP、DP分别平分∠B、∠D，相交于点P，试探究∠P与∠A、∠C的关系.

证明：记线段AD、BP相交于点M，则根据8字模型结论得∠A+∠ABP=∠P+∠ADP ①.

记线段BC、DP相交于点N，则根据8字模型结论得∠P+∠CBP=∠C+∠CDP ②.

因为BP、CP分别平分∠ABC、∠ADC，所以∠ABP=∠CBP，∠ADP=∠CDP.

认识了8字模型与角平分线的结合，在此基础上还可做如下变式：

证明：记线段AD、BP相交于点M，则根据8字模型结论得，所以∠ABC-∠ADC=3（∠P-∠A）.

记线段BC、DP相交于点N，则根据8字模型结论得∠P+∠CBP=∠C+∠CDP，则，所以

进一步可以推广到一般情况：

2.飞镖模型

如图3，试探究∠A、∠B、∠C、∠D的关系.

结论：∠D=∠A+∠B+∠C.

通过对三角形中研究角时一条线的认识，有以下思考：

证法1：（利用三角形内角和定理）连接BC.

在△ABC中，∠A+∠ABC+∠ACB=180°，所以∠A+∠ABD+∠ACD=180°-∠DBC-∠DCB.

在△DBC 中，∠BDC+∠DBC+∠DCB=180°，则∠BDC=180°-∠DBC-∠DCB，所以∠BDC=∠A+∠ABD+∠ACD.

证法2：（构造外角，利用外角结论）连接AD并延长至点E.

根据外角结论，得∠BDE=∠B+∠BAE，∠CDE=∠C+∠CAD，所以∠BDE+∠CDE=∠B+∠C+∠BAE+∠CAD，即∠BDC=∠BAC+∠B+∠C.

实际上在利用外角结论证明时，也可用以下方法：延长线段BD交AC于点M，或者延长线段CD交AB于点N.

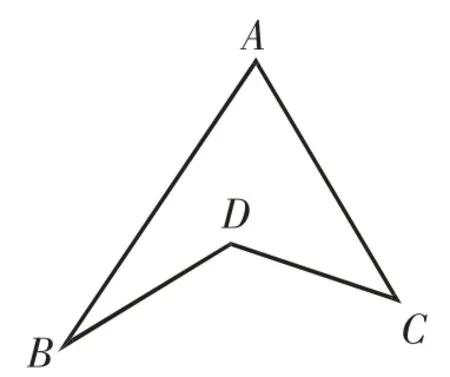
图3

图4

建立在飞镖模型的基础上，将飞镖模型与角平分线结合，有如下问题探究：

如图4，BO、CO分别平分∠ABC、∠ACB，相交于点O，试探究∠A、∠O、∠D的关系.

结论：∠A+∠D=2∠O

证明：由飞镖模型可得：∠O=∠A+∠ABO+∠ACO，∠D=∠O+∠OBD+∠OCD.

因为BO、CO分别平分∠ABC、∠ACB，所以∠ABO=∠OBD，∠ACO=∠OCD.则∠O-∠A=∠D-∠O，故∠A+∠D=2∠O.

认识了飞镖模型与角平分线的结合，在此基础上还可做如下变式：

证明：由飞镖模型可得：∠O=∠A+∠ABO+∠ACO，∠D=∠O+∠OBD+∠OCD.

进一步可以推广到一般情况：

将8字模型、飞镖模型与对角线结合得到了一般性的结论，而三角形中角平分线的一般结论又如何呢？

三、三个结论（三角形中角平分线的结论）

1.两个内角平分线的结论

在△ABC中，∠ABC的平分线和∠ACB的平分线交于点P，如图5，试猜想∠P与∠A的关系，并予以证明.

证明：在△PBC中，∠P=180°-∠PBC-∠PCB.

因为BP、CP分别平分∠ABC、∠ACB，所以∠PBC=

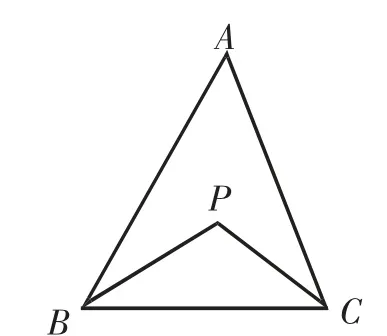
图5

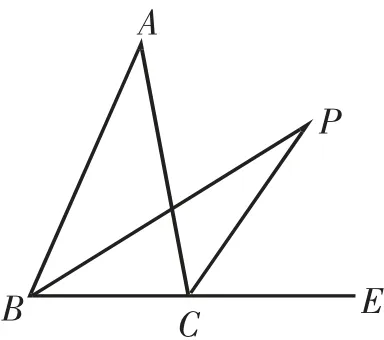
图6

2.一个外角与一个内角平分线的结论

在△ABC中，一个外角∠ACE的平分线和一个内角∠ABC的平分线交于点P，如图6，试猜想∠P与∠A的关系，并予以证明.

证明：因为∠PCE为△PBC的外角，所以∠P=∠PCE-∠PBC.

因为BP、CP分别平分∠ABC、∠ACE，所以∠PBC=

3.两个外角平分线的结论

在△ABC 中，两个外角∠EBC的平分线和∠FCB的平分线交于点P，如图7，试猜想∠P与∠A的关系，并予以证明.

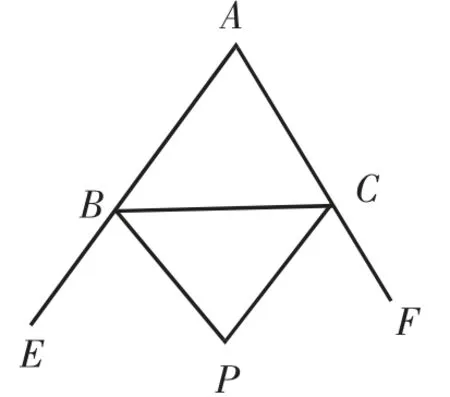
图7

证明：在△PBC中，∠P=180°-∠PBC-∠PCB.

因为BP、CP分别平分∠EBC、∠FCB，所以∠PBC=

建立在三角形中角平分线的结论上，与之方法类似，以上问题均可拓展到一般情况并得到一般性的结论：

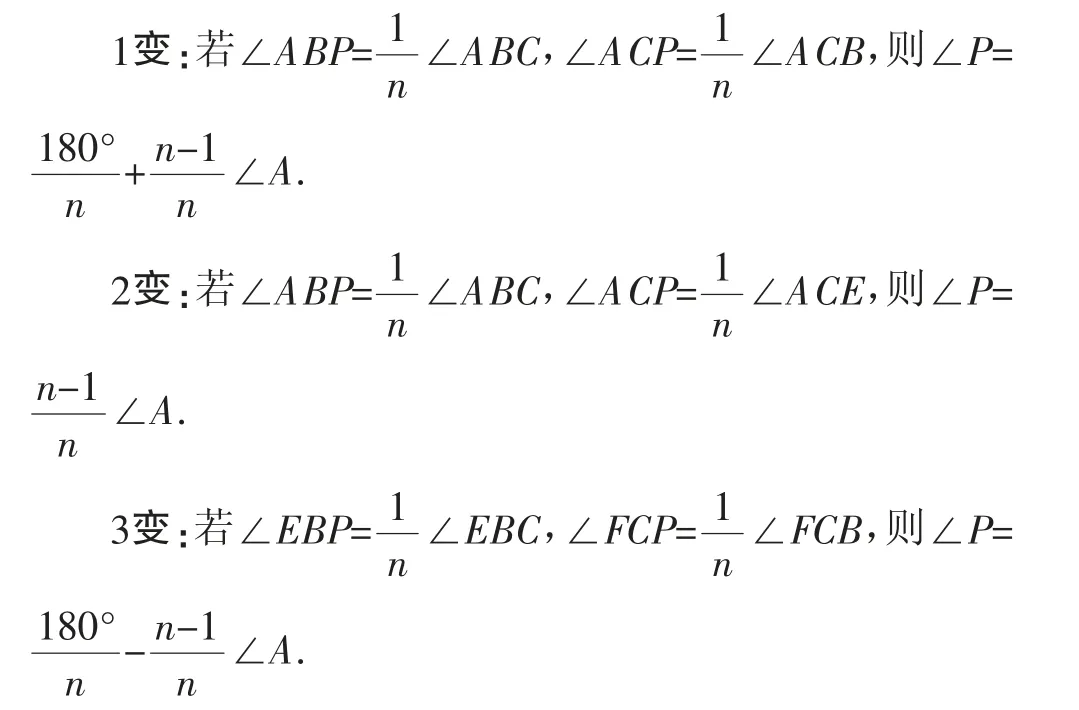
以上内容是对三角形中如何求角这个问题的部分认识，充分掌握好以上问题的结论及证明过程，在适当情况下能起到事半功倍的作用.实际上，不管是三角形中求什么角的问题，核心本质都是首先抓住这个角是什么角，然后充分利用内角和定理或者外角结论进行转化解决.