2019年台州中考数学第16题解法分析与再探究

浙江省宁波市镇海蛟川书院 刘继华

一、试题呈现

（2019年台州）如图1，直线l1∥l2∥l3，A、B、C分别为l1、l2、l3上的动点，连接AB、BC、AC，线段AC交直线l2于点D.设直线l1、l2之间的距离为m，直线l2、l3之间的距离为n，若∠ABC=90°，BD=4，且，则m+n的最大值为___________.

图1

图2

二、解法展示

1.构造相似，利用函数求最值

解法1：如图2，过点B作PQ⊥l2交l1于点P，交l3于点Q，过点A作AF⊥l1交l2于点E，交l3于点F.

设AP=x，则EB=FQ=x.又BD=4，则DE=4-x.

2.利用斜大于直求最值

解法2：如图3，延长AB交l3于点E，作△BCE的中线BO.

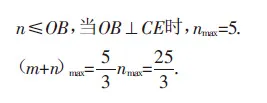
图3

图4

3.构造辅助圆求最值

解法3：如图4，延长AB交l3于点E，构造过C、B、E三点的⊙O.由∠CBE=90°，得OE为直径.

同解法2可得CE=10，则点B在半径为5的半圆CBE上运动，点B到l3距离的最大值即为n的最大值，当⊙O与l2相切时，nmax=5.

4.数形结合，以数解形

解法4：如图5，以B为原点建立平面直角坐标系.

由∠ABC=90°，得kAB·kBC=-1，则=-1，则pq=6a2①.

由BD=4，得点D（-4，0）.

由kAD=kCD，得，则3p+2q=-20 ②.

图5

图6

三、试题变式

1.条件与结论互换变式

变式1：如图6，其他条件与原试题相同，若∠ABC=90°，m=2，n=3，则BD的最小值为___________.

思路点拨：如图7，延长AB交l3于点E，构造过C、B、E三点的⊙O.

图7

2.改变条件变式

表1

现以①和②为例：

变式2：如图8，将“A、B、C分别为l1、l2、l3上的动点”变为“A，B，C分别为l2，l3，l1上的动点”，“BD=4”变为“AD=4”，其他条件、问题与原试题相同.

图8

图9

思路点拨：如图9，当⊙O与l3相切时

变式3：如图10，将“∠ABC=90°”变为“∠ABC=60°”，其他条件与问题和原试题相同.

思路点拨：方法1：如图11，延长AB交l3于点E，构造过C、B、E三点的⊙O，连接OC、OE，作OH⊥l3交⊙O于点G.

图11

由l2∥l3，得

易得CE=10.

因为∠ABC=60°，所以∠CBE=120°，∠COE=120°，∠OCE=∠OEC=30°，CH=HE=5，OH=则CO=，点B在半径为的弧CBE上运动.

点B到l3距离的最大值，即为n的最大值.

当⊙O与l2相切时，点B与G重合，则，故

方法2：事实上，不难发现，当⊙O与l2相切时，△CBE为等腰三角形，，此时n=

3.结论一般化

如图10，其他条件与原试题相同，若∠ABC=θ，BD=a，且=t，则m+n的最大值为___________.

思路点拨：由变式3的方法2，可得

四、探究反思

1.试题解读，实现整体把控

本题以平行线、直角三角形为背景，考查了平行线的性质、特殊三角形的性质与判定、相似、圆的基本性质等核心知识.以往以此图为背景的中考试题，如2013年广东深圳数学中考第13题、2013年海南省中考第14题，图形是固定的，一般利用特殊三角形、相似三角形、平行线等相关知识即可解决，但这道题巧妙融入运动观点，涉及的思想方法更加丰富，渗透了函数思想、方程思想、转化思想、数形结合思想等重要思想方法，使不同能力的学生对试题感悟及解法达到不同水平，“使不同的人在数学上得到不同的发展”.

2.解法反思，积累解题经验

有些学生疑惑为什么别人能想出多种解法，我却一种也想不出.波利亚解题表的精髓就是联想，教师要充分发挥解题表的辐射功能.这道题的突破口就是∠ABC=90°，这个条件使人联想到的方法是直角三角形、相似、圆、勾股定理，k1·k2=-1等.

解法1是常规解法，图形中有直角这一关键条件，学生在已有学习经验积累基础上，比较容易联想到一线三直角，所以辅助线的产生水到渠成，接下来是将边表示出来，当遇到长度未知的线段时，自然想到用字母表示相关线段长度，发展了学生的符号意识，通过相似建立起了两个变量之间的对应关系，函数思想自然而然产生.

图12

图13

解法2与解法3思维要求比较高.直接求最值的困难使学生萌发转化的思想，直角这一特殊条件，容易使人联想到构造直角三角形，构造辅助圆，将m+n的最大值转化为先求n的最大值.

在各类解法中，解法2、解法3解法简洁，值得思考的是，在后续变式中，采用了解法3，构造辅助圆，因为这一解法更能触类旁通，体现实质.例如，当∠ABC=60°时，利用解法2斜大于直，如图12，作△BCE的中线BM，BM的长度是个变量，此种方法看似不适用了，这是因为这种添辅助线的方法没有理解问题本质，若要用解法2，需要构造过C、B、E三点的辅助圆⊙O，连接BO，作ON⊥l2于点N，当ON=BO时，OH为定值，HN最大.

解法4是解析法，是高中方法，适合一小部分初中优秀学生，仅供参考.如果教师在平时教学中抛砖引玉，必然会激发这部分学生的探究欲望.

3.变式教学，提升思维品质

每道中考题都是经过专家精心命制的，如果能细细品味，潜心探究，一定会有意犹未尽之感.作为一线教师，在平时教学中，应该挖掘每道题的潜在价值，变式教学是一种很好的途径.以这道中考题为例，通过条件和结论互换、改变条件、结论一般化等方式进行变式，使学生从多角度、多渠道思考问题，感受条件与条件、条件与结论之间的联系，更深刻地理解问题本质，提升学生的思维能力.通过变式，使学生进一步感悟不同的解法，并逐步内化成为属于他们的自然解法，提升解题能力.