基于分形谐振器的远场超分辨率扫描成像
2019-12-24高强李小秋周志鹏孙磊
高强 李小秋 周志鹏 孙磊
1) (南京电子技术研究所, 南京 210039)
2) (天线与微波技术国防科技重点实验室, 南京 210013)
3) (电子科技大学应用物理研究所, 成都 610054)
为突破传统衍射极限实现远场超分辨率扫描成像, 提出一种基于分形谐振器的微结构阵列用于目标远场超分辨率扫描成像.该阵列基于局域模谐振原理, 将目标的超分辨率信息包含在频谱中传播到远场, 可在远场通过频谱信息判断目标所在位置, 从而不借助于格林函数实现超分辨率实时成像, 成像过程简单方便.基于分形谐振器的设计使阵列具有多频点工作的特点, 最终实现了λ/10的超分辨率成像.结合分形谐振器一阶谐振和三阶谐振的特点, 提出一种可有效提升成像效率的新型的扫描成像方法.
1 引 言
超分辨率最早应用于光学亚波长成像, 即在物体近场范围内探测物体本身包含的精细结构特征所对应的高频分量来实现超分辨率[1-4].Born和Wolf根据光学成像过程得出:一束光入射到1个具有超精细结构(精细尺度小于λ/2)的物体上,入射波会被转换成传播波和凋落波; 传播波分量能够传播到探测器, 凋落波分量只能存储在结构表面, 前者与物体本身对应的低频分量相关联, 后者与物体包含的精细结构对应的高频分量(亚波长信息)相关联; 亚波长信息通过凋落波向外传播, 而凋落波分量的幅度呈指数衰减而无法传播到远场参与成像, 影响超分辨率成像的实现[5].因此, 如何获取亚波长信息(高频分量)是实现超分辨率成像的关键.在 1984年, Pohl等[6]提出利用近场探针扫描物体表面来实现亚波长成像, 缺点是近场扫描光学显微镜需要消耗较长的时间来逐点扫描, 因此, 无法实时高效成像.随后, 同时具有负介电常数和负磁导率的完美透镜被提出来, 该透镜可以将凋落波幅度进行放大, 然后在透镜的出射面扫描成像[7-10].其局限性是依然是近场成像, 因为凋落波的性质并没有发生变化.
将凋落波转换为传播波辐射到远场是一种实现远场超分辨率成像的有效方法.文献[11]提出一种远场超级透镜, 它可以将放大后的凋落波通过紧邻的耦合元件转换成传播波, 传播到远场参与成像, 实现超分辨率成像.但是其缺点是耦合元件设计难度较大, 且转换的传播波的频率范围有限, 只能让一部分凋落波分量转化成传播波, 因此该远场成像透镜的超分辨率能力也很有限[12].另一种方法是在微波频段, Fink团队[13-15]提出由亚波长周期阵列构成的谐振超透镜, 该周期结构可将凋落波转换为传播波, 并将目标的空间信息包含在频谱分量中, 用于超分辨率图像的重构.该超透镜为三维立体结构, 尺寸较大且不便于加工, 在此基础上则提出了二维平面超透镜[16-18], 具有剖面低的优点,可实现二维拓展目标的成像.该方法的关键在于需要获得成像目标与收发天线之间的格林函数, 文献[19]则对于亚波长小球加载的情况, 从解析上分析了超分辨率实现的条件, 并通过仿真进行验证.但是, 对于复杂的成像环境, 获取准确的格林函数极其困难[20-23].文献[24]分析了局域模谐振现象:当亚波长谐振器进行有限周期排列时, 产生的谐振模式会将电磁场束缚在亚波长的空间尺寸范围内.这些局域模谐振模式可以将空间信息与频率相对应, 并传播到远场, 这样就可以直接根据频谱信息来实现实时成像, 而不需要格林函数.文献[25]则基于这种原理提出一种基于开口环谐振器的远场扫描成像阵列, 但仍需要进行逐个单元扫描, 成像效率有限.本文同样基于局域模谐振原理, 并结合分形结构的特性, 设计一种具有多频点工作能力的远场超分辨率扫描成像阵列.该结构可将目标的细节信息传播到远场, 并通过远场频谱进行图像重构, 实现超分辨率成像.由于分形结构多阶谐振的特性, 将其中一阶和三阶谐振特性组合利用, 提出一种高效率扫描成像方法.
2 原理及结构设计
首先要分析电磁波在这种局域模谐振媒质内部的特性, 这方面已经有很多分析的方法, 其中一种就是基于偶极子模型分析谐振器单元之间的耦合[26,27], 将亚波长谐振器等效为电偶极子和磁偶极子的叠加, 从而分析实现远场辐射的原理.从这种分析方法中可以发现一个现象, 尽管所有谐振单元尺寸一样, 但会产生N个不同频率的谐振模式, 实际上这是由谐振器之间的耦合引起的, 并且谐振峰的数量和单元的数量是相对应的.然而由于简并模式和对称性的原因, 实际谐振频点存在重合的情况, 获得的信息数量受到了限制.文献[16]的研究表明, 获得的频谱信息与成像目标的空间信息是相互对应的, 因此可以通过一些措施和方法来建立谐振频率和谐振器空间位置之间的联系, 从而通过频谱信息来得到目标的空间位置, 进而成像.基于这种现象, 可以利用分形结构一些独特的特性进行相应的结构设计和成像.
分形结构是指局域与整体具有某种自相似性的结构, 这种自相似性用来进行谐振器的设计时会产生多频点谐振的特性.本节内容则基于这种多频点谐振特性进行分形远场扫描微结构阵列的设计.这里采用“H”形谐振器作为初始谐振单元, 进行三阶分形设计后得到的结构模型如图1(a)所示.图中棕色部分为金属贴片, 蓝色部分为刻蚀出的槽,金属印刷在FR4介质基板上, 相对介电常数为4.2, 损 耗 正 切 角 tanδ= 0.001, 厚 度 为 1 mm,其中l1=l2=10 mm,l3=l4=6mm,w1= 1.2mm,w2= 0.4 mm,px=py= 20 mm.

图1 (a)分形谐振器单元的物理尺寸; (b)开关设置模型Fig.1.(a) Physical dimensions of fractal resonator cell; (b) switch setup model.
下面对该分形谐振器单元进行远场频谱仿真,仿真设置从 1 GHz到 6 GHz, 一个小偶极子天线放置在单元近场范围, 在距离单元3000 mm处放置一个远场探针来监测远场频谱, 如图2(a)所示.为了实现扫描成像, 可在槽间加载开关来控制该谐振器使其具有可切换的工作状态, 实际工程应用中可采用光导开关, 并通过激光来控制, 可以有效提升扫描成像的速度.图1(b)中的黑色部分即为加载的开关, 记为 A, B1, B2, B3, B4.状态 1:当所有开关都断开时, 整个分形谐振器被激励, 处于工作状态, 在图2(b)远场频谱的黑色曲线有3个明显的谐振峰, 谐振频率分别为 1.5, 3.5, 5.1 GHz,分别代表着三阶分形单元的谐振频率.状态2:当所有开关闭合时, 加载开关位置处短路, 分形谐振器处于非工作状态, 1—6 GHz频率范围内无谐振现象, 如图2(b)红色曲线所示, 且幅度也远小于谐振时的频谱幅度.也就是说, 通过这两种状态引起的远场频谱变化可判断分析谐振器单元上面是否存在激励源, 从而确定激励源的位置, 进而成像.这里的一阶谐振频率为1.5 GHz, 单元周期则为λ/10.并且远场频谱中的每个谐振频点都可用来进行扫描成像, 在实际应用中可根据实际环境具有更多的选择性, 体现了这种分形结构多频点工作的优点.

图2 分形谐振器单元远场频谱仿真模型及两种工作状态下的远场频谱 (a)远场频谱仿真模型; (b)两种工作状态下的远场频谱Fig.2.Far-field spectrum simulation setup of fractal resonator cell and simulated far-field spectra of two working status:(a) Far-field spectrum simulation setup; (b) far-field spectra of two working status.
值得注意的是, 文献[25]将单个谐振器单元作为一个成像像素点, 本文则不同, 提出的分形单元具备更多的工作状态, 具体可以细分为多个像素点.接下来对一阶和三阶谐振进行组合使用, 根据谐振器的谐振情况将该分形单元划分为5个区域,如图1(b)所示, 分别对应1个一阶谐振和4个三阶谐振.这样三阶谐振就将整个分形谐振器细分为4个区域, 具有了4个像素点.对于该4个像素点区域, 打开其中1个区域的开关, 关闭其他开关,通过开关通断得到的频谱即可判断该区域是否存在激励源, 成像像素得到细化, 提升了成像分辨率.
为了避免相邻像素点区域对远场频谱的影响,须要分析单元之间的耦合问题, 模型结构如图3所示.此时, 一个激励源位于单元 1 的近场区域, 初始状态时两个单元都处于非工作状态, 在远场频谱中不会观察到谐振现象.当处于状态1时, 单元2的5个开关闭合, 断开单元1的5个开关, 此时单元1处于工作状态, 在远场频谱中会观察到明显的谐振现象, 如图4黑色曲线所示, 谐振频率位于1.47 GHz; 当处于状态 2 时, 单元 1 的 5 个开关闭合, 断开单元2的5个开关, 此时单元2处于工作状态, 可以看到此时的远场频谱远小于状态1时,可以判断单元1和2之间的耦合可以忽略不计, 如图4红色曲线所示.

图3 一阶谐振的两种工作状态设置Fig.3.Two working status setup of the first resonance.

图4 一阶谐振两种工作状态的远场频谱Fig.4.Far-field spectra of the first resonance at two working status.
然后对三阶谐振进行类似的分析, 模型结构如图5(a)所示, 得到的结果与一阶谐振类似, 相邻像素点区域之间的耦合可以忽略不计.
3 分形微结构阵列的远场超分辨率成像特性验证与分析
利用上面提出的分形单元结构进行多频点远场扫描成像微结构阵列的设计以及超分辨率特性的分析.将该分形谐振器单元组成一个8 × 8的周期阵列放置在自由空间中, 周期为px=py=20 mm, 并对每个单元进行编号, 从 (1, 1)到 (8, 8),如图6(a)所示, 每个单元代表着一个成像像素点.这里选择60个点源组成一个笑脸形的源成像目标, 放置在阵列上方5 mm处, 然后在距离阵列结构10λ处放置4个覆盖1—6 GHz的宽带Vivaldi天线来接收频谱信息, 结构模型如图6(b)所示.根据前面分析的结果, 每个完整的分形谐振器可以代表4 个像素点, 总共就要 8 × 8 × 4 = 256 个像素点, 正常的扫描成像过程是对这256个像素点进行逐点扫描, 然后成像.这里基于该分形单元本身的结构特性, 提出一种改进的成像方法, 成像步骤如下:
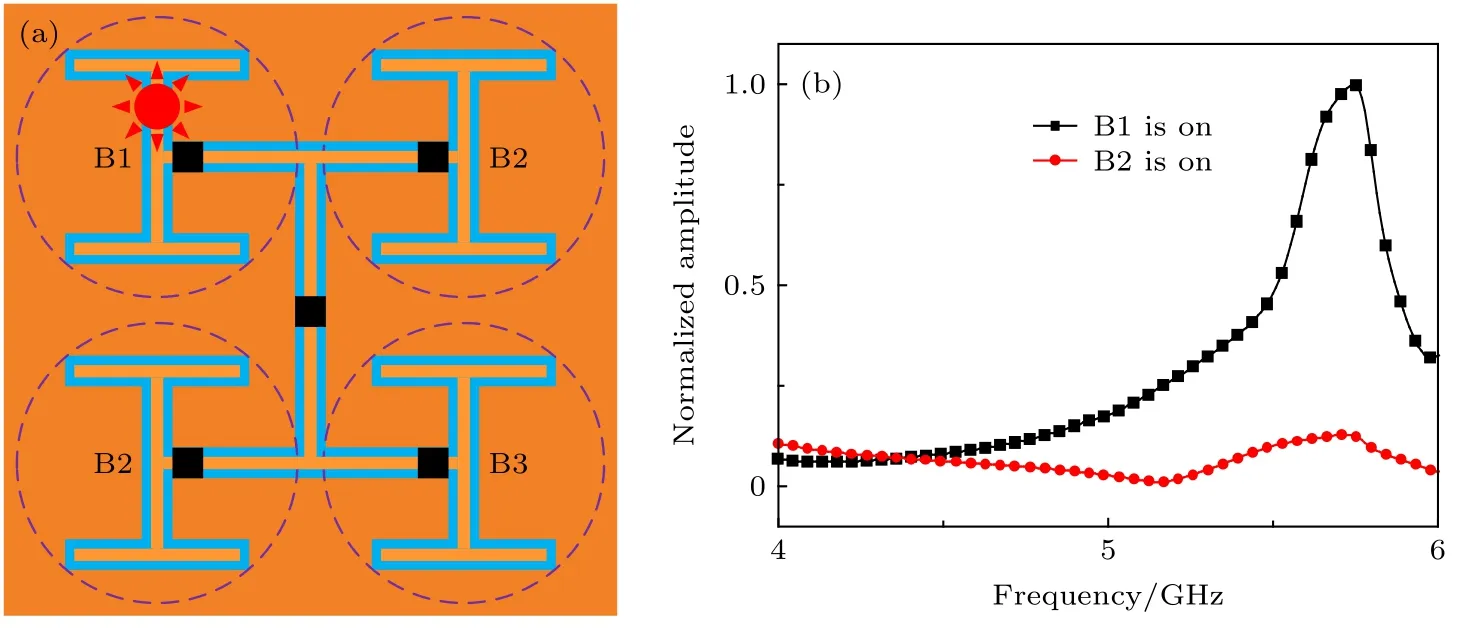
图5 三阶谐振的两种工作状态设置及远场频谱 (a)工作状态设置; (b)远场频谱Fig.5.Two working status and far-field spectra of the third resonance:(a) Working status setup; (b) far-field spectra.

图6 分形微结构阵列编号及成像模型设置 (a)编号模型; (b)成像模型Fig.6.Number of fractal microstructure array and imaging model:(a) Number model; (b) imaging model.
1)初始状态时所有单元都处于非工作状态,所有点源同时激励, 然后打开编号(1, 1)单元的开关A, 使其工作;
2)此时4个宽带Vivaldi天线会接收到具有谐振现象的频谱信息, 将其中的一阶谐振峰值幅度叠加后填充到编号(1, 1)单元代表着的像素点中;
3)关闭编号 (1, 1)单元的开关A, 打开编号(1, 2)单元的开关A, 重复步骤1和2的过程, 将谐振峰值幅度填充到编号(1, 2)单元代表着的像素点中;
4)依次类推, 对所有单元进行同样的操作, 最后得到一个8 × 8的成像矩阵, 利用MATLAB进行画图成像.
在光学成像里, 相邻光斑的幅度相差一倍以上, 认为二者是可分辨的, 光斑之间的距离即为分辨率.这里一个单元大小视为一个像素点, 在成像结果中, 有激励源和无激励源的相邻像素点幅度相差一倍以上, 认为二者可分辨, 成像分辨率即为单元周期大小.归一化的成像结果如图7(a)所示, 从图中可以确定32个单元存在成像目标源, 然后将这32个像素点每个细分为4个小像素点, 总共128个新像素点, 对其进行重新编号从1到128,然后进行同样的成像.
归一化的成像结果如图7(b)所示, 通过二次编号扫描, 将成像像素进行细化, 笑脸形的源成像得到了很好的呈现, 其轮廓清晰, 验证了所提出结构实现远场扫描超分辨率成像的有效性.新提出的扫描成像方法针对文中案例总共需要 8 × 8 + 32 ×4 = 192次扫描, 相对于正常的 256次扫描过程,节省64次的扫描时间.改进的成像方法增加了二次编号的过程, 这个过程可通过计算机编程来实现, 从而可忽略二次编号过程带来的时间影响.因此, 改进的成像方法在成像效率上可得到有效的提升.该结构可以应用在医学成像、无损检测以及电磁泄露等相关领域中.
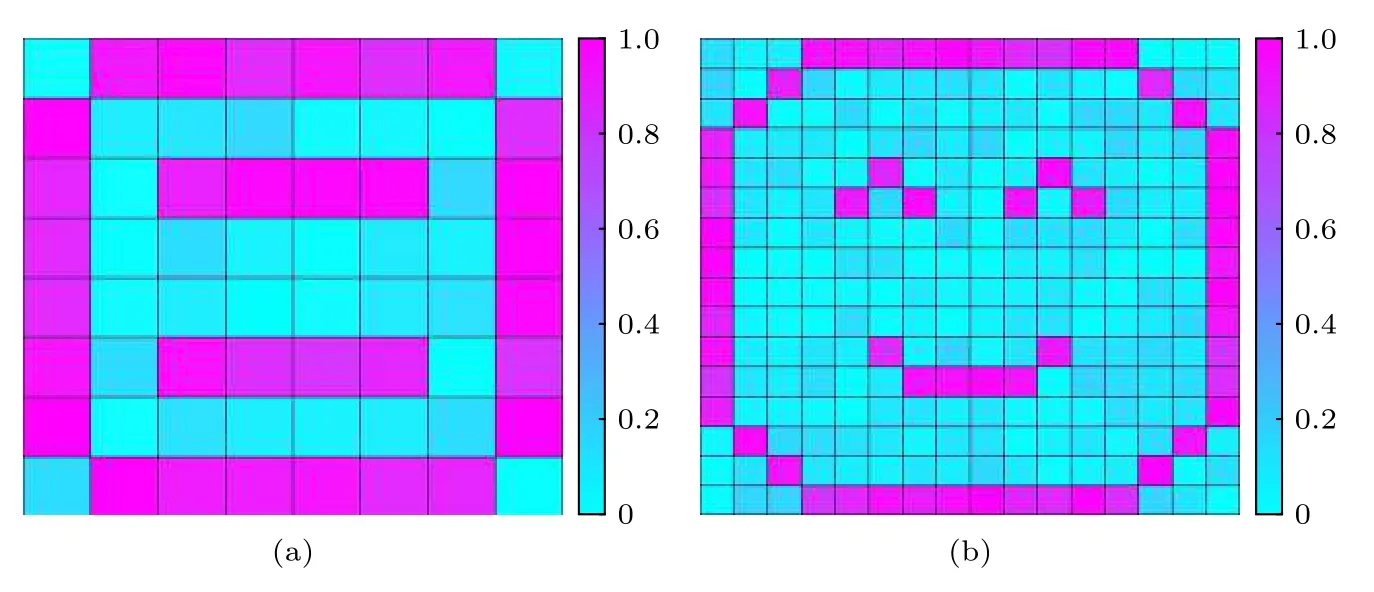
图7 分形微结构阵列远场超分辨率扫描成像结果 (a) 8 × 8 像素点成像结果; (b) 16 × 16 像素点成像结果Fig.7.Far-field super-resolution scanning imaging results of microstructure array:(a) 8 × 8 pixel imaging result; (b) 16 × 16 pixel imaging result.
4 结 论
亚波长谐振器进行周期排列后, 电磁波会被束缚在亚波长尺寸范围, 所形成的模式可以携带物体的细节信息, 并可以辐射到远场, 这些信息与频谱直接相关联, 通过远场频谱就可以直接进行成像,而不需要获取格林函数.本文基于这个原理, 并利用分形结构所具有的多频点工作特性, 设计了一种具有多频点工作能力的远场超分辨率扫描成像微结构阵列, 实现了的超分辨率成像.该微结构阵列不仅具有多频点的工作能力, 还可以将一阶谐振和三阶谐振结合起来, 提出了一种新的扫描成像方法, 先对目标进行粗像素扫描, 确定目标位置后再进行细像素扫描, 获得成像, 相对于已有的方法,可有效提升成像效率.
