基于枝节加载多模谐振器的电调微波滤波器设计

贾建科，王新宽，郑春来，耶晓东

(陕西理工大学 物理与电信工程学院，陕西 汉中 723000)

0 引言

认知无线电技术[1-2]能够利用有限的频谱资源，缓解频谱资源紧张的现状，同时该技术能识别所需频段并自我决定和调节所需频段，工作在可调的工作频带中。频率可调滤波器可以满足该技术需要，使系统小型化并减小系统的插入损耗。微波电调滤波器可以实现滤波器的工作频率和带宽可调，电调滤波器在不改变系统硬件结构的基础上，实现了滤波器工作频率和带宽的调节。微波电调滤波器也可称为微波可重构滤波器，是通过调节固定电路的偏置电压调节滤波器的频率响应，实现滤波器的频率和带宽可调[3]。现有文献给出了电调滤波器的设计，但所设计的电调滤波器存在带外衰减不理想，通带选择性不理想的问题。文献[4]提出的可重构双通带滤波器采用E型微带谐振器，实现了滤波器频率的电调，但滤波器尺寸大，带外衰减不理想；文献[5]利用T型微带谐振器设计的频率可调带通滤波器，尺寸大，通带选择性不理想，且滤波器的频率调节范围较小。文献[6]利用高低阻抗线微带谐振器设计的电调带通滤波器尺寸相对大，带外衰减不理想。基于此，提出了一种基于枝节加载微带线多模谐振器的电调滤波器，实现了滤波器的小型化，并利用新型的频变耦合结构引进新的传输零点，改善了滤波器的带外衰减和通带选择性。

枝节加载的微带线多模谐振器由于加载枝节的微扰，兼并模分裂，利用该谐振器设计微波滤波器，实现微波滤波器的小型化[7-8]。通过控制加载在谐振器末端和加载枝节上的变容二极管的容值大小，可改变微带线的电长度，从而改变谐振单元的谐振频率，控制滤波器中心频率的变化，实现微波滤波器的频率可调，满足认知无线电技术的需要。本设计在分析电调枝节加载微带多模谐振器的基础上，利用双端短路的枝节加载微带多模谐振器和变容二极管设计电调微波滤波器。

1 枝节加载多模谐振器谐振(SLR)机理分析

枝节加载多模谐振器是在双端短路或开路的微带线中心位置加载短路或者开路枝节，因而枝节加载多模谐振器有4种结构，分别为开路枝节加载的双端开路微带谐振器、开路枝节加载的双端短路微带谐振器、短路枝节加载的双端开路微带谐振器、短路枝节加载的双端短路微带谐振器[9-12]。下面主要讨论开路枝节加载的双端开路微带谐振器和短路枝节加载的双端短路微带谐振器的谐振机理。

1.1 开路枝节加载的双端开路多模微带谐振器

根据传输线理论，传输线上任意点的电压和电流可表示为：

U(θ)=ULcosθ+jILZ0sinθ

(1)

(2)

由式(1)、(2)可得传输线上任意点的输入阻抗为：

(3)

电长度为θ的无耗传输线的转移矩阵为：

(4)

则从传输线左侧向右看去的输入导纳为：

(5)

由式(5)可知传输线终端开路时输入导纳为：

(6)

由式(5)可知传输线终端短路时输入导纳为：

(7)

根据式(5)可知，对于结构复杂的多模微带谐振器，分析其谐振特性时，根据谐振器的结构求出谐振器的转移矩阵ABCD矩阵，再结合式(6)、式(7)就可求出谐振器的输入导纳。最后根据谐振条件Im(Yin)=0可分析谐振器的谐振特性。

根据谐振条件Im(Yin)=0和式(6)可得，双端开路的传输线谐振器是二分之一波长谐振器，谐振器的电长度θ=kπ，k为整数。对于微带线谐振器，其谐振频率为:

(8)

其中：c为光速，L为传输线谐振器的长度，εeff为传输线谐振器的介质的等效介电常数。当k=1，即θ=π时可得第一谐振频率，当k≥2时，可依次得到其他高次谐振频率。

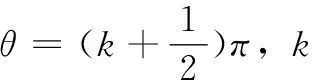
(9)

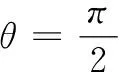
双端短路的传输线谐振器是二分之一波长谐振器，第一谐振频率：

(10)

其中：c为光速，L为传输线谐振器的长度，εeff为传输线谐振器的介质基板的等效介电常数。

开路枝节加载的双端开路微带谐振器是在双端开路的微带谐振器的中间加载开路枝节，结构如图1(a)，开路谐振器的几何长度为2L1，电长度为2θ1，特性阻抗为Y1，开路枝节的几何长度为L2，电长度为θ2，特性阻抗为Y2。该谐振器结构对称，呈轴对称分布，可以利用奇偶模理论进行分析。奇模分析时，对称面处等效为电壁，可用接地等效；偶模分析时，对称面处等效为磁壁，可用开路等效。图1(b)和(c)分别为奇模等效电路和偶模等效电路[5]。

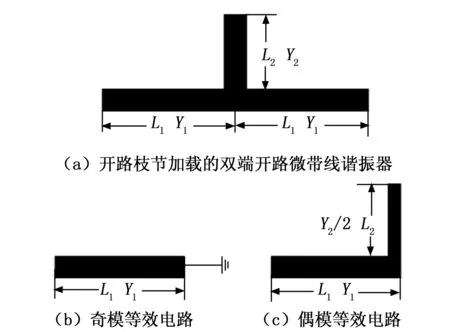
图1 结构图

奇模等效电路为单端短路的传输线谐振器，是四分之一波长谐振器，由式(9)可知奇模第一谐振频率为：

(11)

偶模等效电路为双端开路的传输线谐振器，是二分之一波长谐振器。为分析方便，令开路枝节的特性导纳Y2=2Y1，根据式(8)则偶模第一谐振频率为：

(12)

改变谐振器L1和开路枝节L2的长度就可改变谐振器的奇模和偶模谐振频率。当奇偶模频率靠近，并辅以强的外部耦合就可构成带通滤波器[13-14]。

1.2 短路枝节加载的双端短路多模谐振器

短路枝节加载的双端短路微带谐振器是在双端短路微带谐振器的中间加载短路枝节，结构如图2(a)，短路谐振器的几何长度为2L1,电长度位2θ1，特性阻抗为Y1，短路枝节的几何长度为L2，电长度为θ2，特性阻抗位Y2。同理该谐振器结构对称，呈轴对称分布，也可以利用奇偶模理论进行分析。奇模分析时，对称面处等效为电壁，可用接地等效；偶模分析时，对称面处等效为磁壁，但加载的是短路枝节，因此偶模等效电路在加载枝节末端接地。图2(b)和图2(b)分别为奇模等效电路和偶模等效电路。奇模等效电路为双端短路的传输线谐振器，是二分之一波长谐振器，奇模第一谐振频率为：

图2 结构图

(13)

偶模等效电路为双端短路的传输线谐振器，也是二分之一波长谐振器[15-17]。为分析方便，令开路枝节的特性阻抗Y2=2Y1，则偶模第一谐振频率为：

(14)

同理，改变双端短路谐振器L1和加载短路枝节L2的长度就可改变奇偶模谐振频率，同时辅以强的外部耦合就构成了带通滤波器[7]。

2 枝节加载的频率可调多模谐振器

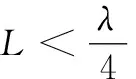
对于开路枝节加载的双端开路谐振器，在3个开路端串联变容二极管就可构成枝节加载的电调谐振器[8]。根据变容二极管加载位置的不同，枝节加载电调谐振器可分为4种类型，分别为终端加载变容二极管，另一端短路的微带谐振器；终端加载变容二极管，另一端开路的微带谐振器；中间加载变容二极管，一端开路，另一端短路的微带谐振器；中间加载变容二极管，两端都开路。本设计选用的是终端加载变容二极管，另一端短路的微带谐振器，同理该谐振器结构对称，呈轴对称分布，也可以利用奇偶模理论进行分析。奇模分析时，对称面处等效为电壁，可用接地等效；偶模分析时，对称面处等效为磁壁，但加载的是短路枝节，因此偶模等效电路在加载枝节末端接地。其电路如图3(a)，奇模等效电路如图3(b)，偶模等效电路如图3(c)。奇模等效电路由变容二极管Cv1和二分之一波长微带线谐振器组成，利用奇偶模理论分析时，谐振器右端看作电壁，可等效接地。根据奇模等效电路和传输线理论可得其奇模输入导纳为：

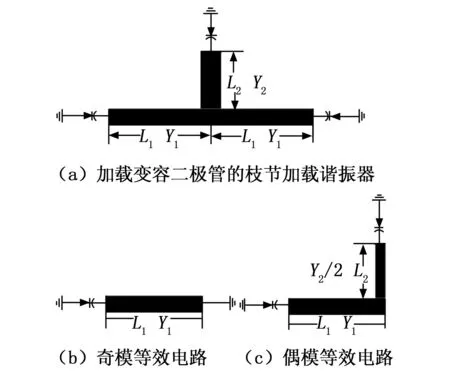
图3 电路图

Yin_odd=-jY1cotθ1+jωc1

(15)

其中：Y1为微带线谐振器L1的特性导纳，θ1为微带线谐振器L1的电长度，c1为加载变容二极管Cv1的容值。根据传输线谐振器谐振条件，由式(15)可得变容二极管Cv1的容值c与谐振器奇模谐振频率fodd的关系为：

(16)

由式(16)可知，随着加载的变容二极管Cv1容值c1的增大，奇模谐振频率fodd减小。改变加载变容二极管Cv1的容值，可改变谐振器的奇模谐振频率。

偶模等效电路如图3(c)所示，偶模等效电路由二分之一波长谐振器L1、加载枝节L2、变容二极管Cv1和变容二极管Cv2组成。根据传输线理论可得该电调谐振器的偶模输入导纳为：

(17)

其中：

式(17)中，Y1为微带线谐振器L1的特性导纳，θ1为微带线谐振器L1的电长度，Y2为微带线谐振器加载枝节L2的特性导纳，θ2为微带线谐振器加载枝节L2的电长度，c1为加载变容二极管Cv1的容值，c2为加载变容二极管Cv2的容值，ωeven为偶模谐振角频率。根据传输线谐振器谐振条件，由式(17)可知变容二极管Cv1的容值c1和变容二极管Cv2的容值c2与谐振器偶模谐振频率feven有关，随着加载的变容二极管Cv1容值c1和变容二极管Cv2容值c2增大，谐振器偶模谐振频率feven减小。因此改变加载变容二极管的容值，就可改变谐振器的偶模谐振频率。

根据式(11)、(12)可知，枝节加载的多模微带线谐振器的奇模谐振频率与谐振器的长度L1有关，增大谐振器长度，奇模谐振频率减小，偶模谐振频率与谐振器的长度L1和加载枝节的长度L2有关，增大L1和L2的长度，偶模谐振频率减小。根据式(16)、(17)可知，在不改变枝节加载谐振器几何长度的基础上，通过在谐振器和加载枝节的末端加载变容二极管的方法，可改变谐振器的奇模和偶模谐振频率。改变加载的变容二极管的容值，等效为改变谐振器和加载枝节的几何长度，从而改变谐振器的谐振频率。增大谐振器两端加载的变容二极管Cv1的容值，减小谐振器的奇模谐振频率，增大谐振器两端加载的变容二极管Cv1和加载枝节末端加载的变容二极管Cv2的容值，可减小偶模谐振频率。通过强的外部耦合，使该电调谐振器的奇模谐振频率和偶模谐振频率构成一通带，改变变容二极管Cv1多和Cv2的容值，可实现滤波器工作频率的电调。多模谐振器的奇模谐振频率和偶模谐振频率二者间的耦合系数M为：

(18)

由式(18)可知，由多模谐振器构成的微波带通滤波器，改变多模谐振器的奇模谐振频率和偶模谐振频率，就可改变滤波器的带宽。因此改变变容二极管Cv1和Cv2的容值，不仅实现了微波滤波器工作频率的电调，还实现了微波滤波器工作带宽的电调。图4(a)给出了奇模谐振频率随加载变容二极管容值的变化曲线。可知随着变容二极管容值的增大，谐振器奇模谐振频率减小。当变容二极管容值较小时，奇模谐振频率变化大，随着变容二极管容值增大，奇模谐振频率变化减小。改变加载在谐振器两端的变容二极管的容值可改变谐振器的奇模谐振频率。图4(b)给出了偶模谐振频率随加载变容二极管容值的变化曲线。随着加载在谐振器短路端和加载枝节短路端可变二极管容值的增大，谐振器的偶模谐振频率减小。改变加载在谐振器两端的变容二极管的容值也可改变谐振器的偶模谐振频率。因此通过在谐振器的两端加载变容二极管就可实现谐振器谐振频率的电调[18-20]。

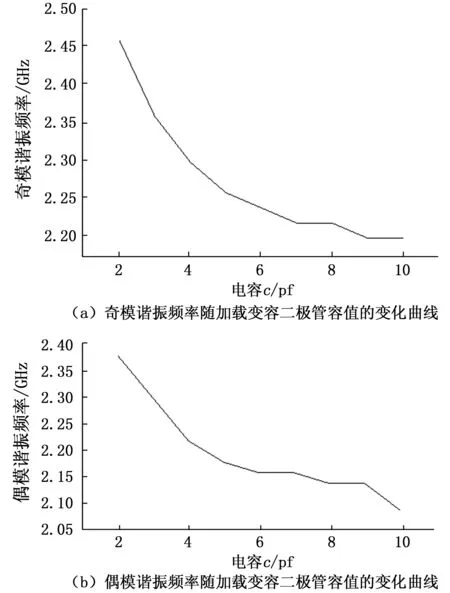
图4 谐振频率随加载变容二极管容值的变化曲线

本设计通过在开路枝节加载的双端开路谐振器的开路端和加载枝节端加载变容二极管的方法构成了一电调微带多模谐振器，并利用该电调谐振器设计电调滤波器。枝节加载的谐振器具有多模谐振特性，因此利用电调枝节加载谐振器不仅可实现滤波器的小型化，同时实现滤波器工作频率和带宽的电调。

3 枝节加载多模谐振器的电调滤波器设计

枝节加载多模谐振器由于加载枝节的微扰，传输线谐振器简并模分裂，形成奇模和偶模谐振频率，辅以强的耦合方式就可构成带通滤波器[4]。因此由一个枝节加载谐振器设计的微波滤波器可以有效减小滤波器的尺寸，实现滤波器的小型化。本文利用枝节加载的电调多模谐振器设计了一电调微波滤波器，通过平行耦合线馈电，在枝节加载谐振器的开路端和加载的枝节上串联变容二极管实现微波滤波器工作频率的电调。该电调微波滤波器由枝节加载谐振器、变容二极管、平行耦合馈线组成，滤波器拓扑结构如图5所示。

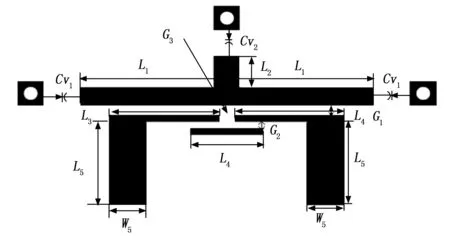
图5 枝节加载谐振器的电调微波滤波器

谐振器由两端开路的谐振器和加载的短路枝节组成，其长度为2L1，加载的短路枝节长度为L2。在谐振器的开路端和加载枝节的短路端串联变容二极管Cv1和Cv2，L3为平行耦合馈线，馈线末端放置耦合线L4。介质基板材料选用Rogers RT/Duroid 5880，相对介电常数为2.65，介质基板厚度h=1 mm。谐振器的长度决定奇模谐振频率，而谐振器的长度和加载枝节长度决定偶模谐振频率，改变谐振器和加载枝节的长度就可改变滤波器的工作频率和带宽。通过改变变容二极管的偏置电压，就可改变变容二极管的容值，实现滤波器工作频率和带宽的电调。因此在谐振器的短路端和加载枝节端加载可变电容器和偏置电路，改变偏置电路的偏置电压，就可改变变容二极管的容值，实现滤波器频率的电调。

该滤波器的馈电方式采用平行耦合线L3馈电，平行耦合线L3和谐振器枝节L1之间实现电耦合。微带线L5是阻抗匹配线，其宽度为W5。为了增强滤波器的通带选择性，引入源和负载耦合的方法，在滤波器的上边带引入了一传输零点，该源和负载的耦合是容性耦合。输入输出平行耦合线L3的末端相互靠近，二者之间实现耦合，即源和负载耦合，耦合方式是电耦合，二者之间的间距为G3。减小两平行耦合线L3的间距G3的值，当G3=2 mm时，通带右边未引入传输零点，随着间距G3的减小，当G3=0.4 mm时，通带右边引入了一个传输零点TZ3，如图6所示。图6给出了引进源和负载耦合时，滤波器通带选择性的变化曲线。从图6可知，引进源和负载耦合，即减小输入输出馈线末端的距离G3，通带右边引入新的传输零点，滤波器通带选择性增强。在馈线L3末端放置耦合线L4，进一步增强了源和负载的耦合，滤波器的通带选择性增强。图7给出了添加耦合线L4后，滤波器通带选择性的变化曲线，从图7可知，添加耦合线L4后，滤波器过渡带更加陡峭，通带选择性进一步加强。馈线L3和耦合线L4的间距为G2，放置耦合线L4后滤波器的传输零点TZ2和TZ3更靠近通带，滤波器的通带选择性进一步增强。耦合线L4的长度、馈线L3和耦合线L4的间距G2的大小都影响传输零点TZ2和TZ3的位置。馈线L3与谐振器的间距为G1，馈线末端耦合线L4与平行耦合馈线L3间距为G2，谐振器末端通过过孔接地，过孔直径为d。通过仿真优化可得该滤波器的尺寸，L1=45 mm，W1=2 mm，L2=3 mm，W2=4 mm，L3=35.9 mm，W3=0.4 mm，L4=10 mm，W4=0.2 mm，L5=24.5 mm，W5=5.6 mm，G1=0.1 mm，G2=0.2 mm，d=0.8 mm。最后仿真了该频率可调滤波器，仿真结果如图8所示。图8给出了变容二极管容值与滤波器工作频率的变化关系，滤波器的工作频率随着变容二极管容值的增大在减小。

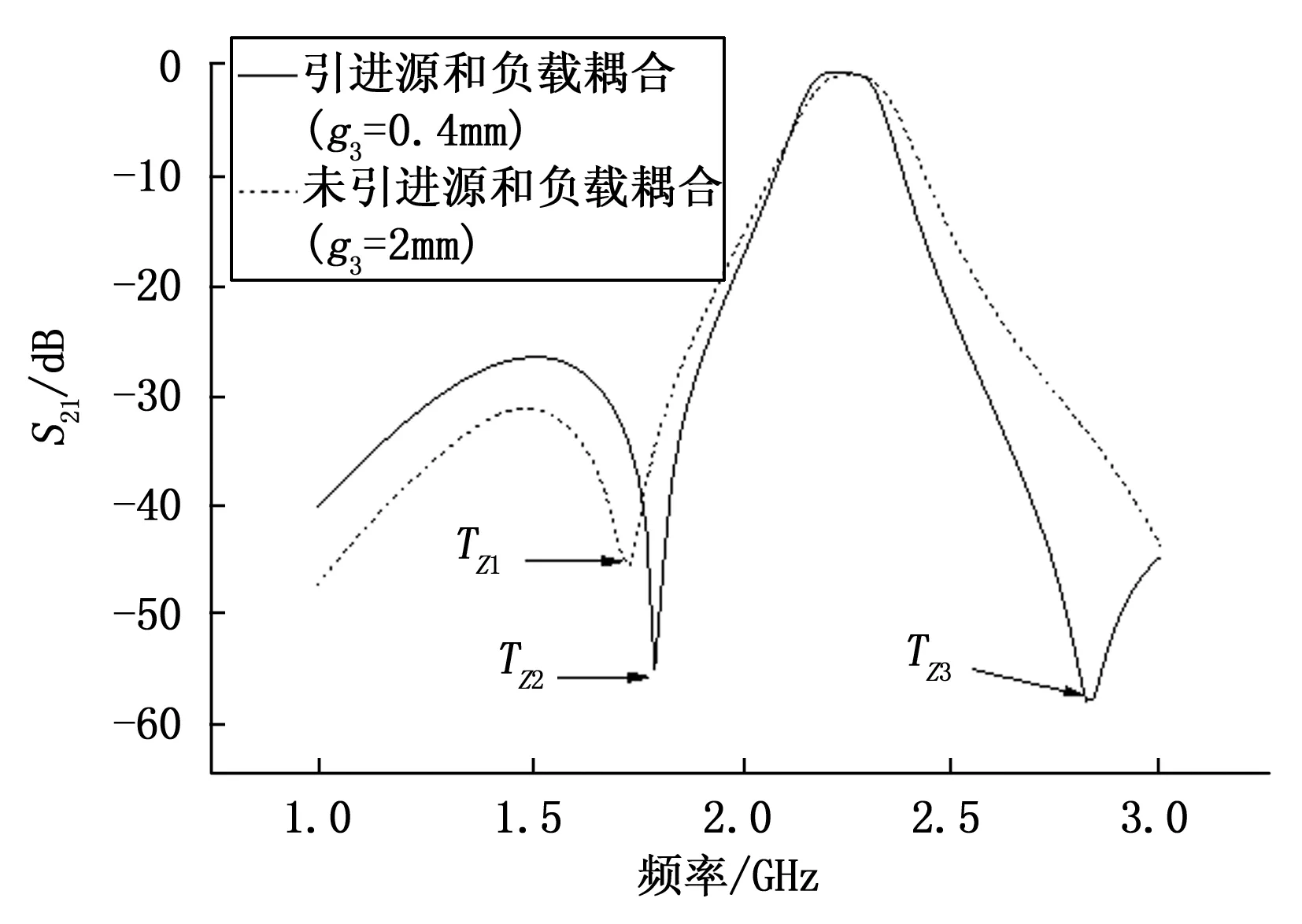
图6 引进源和负载耦合时通带选择性的变化曲线

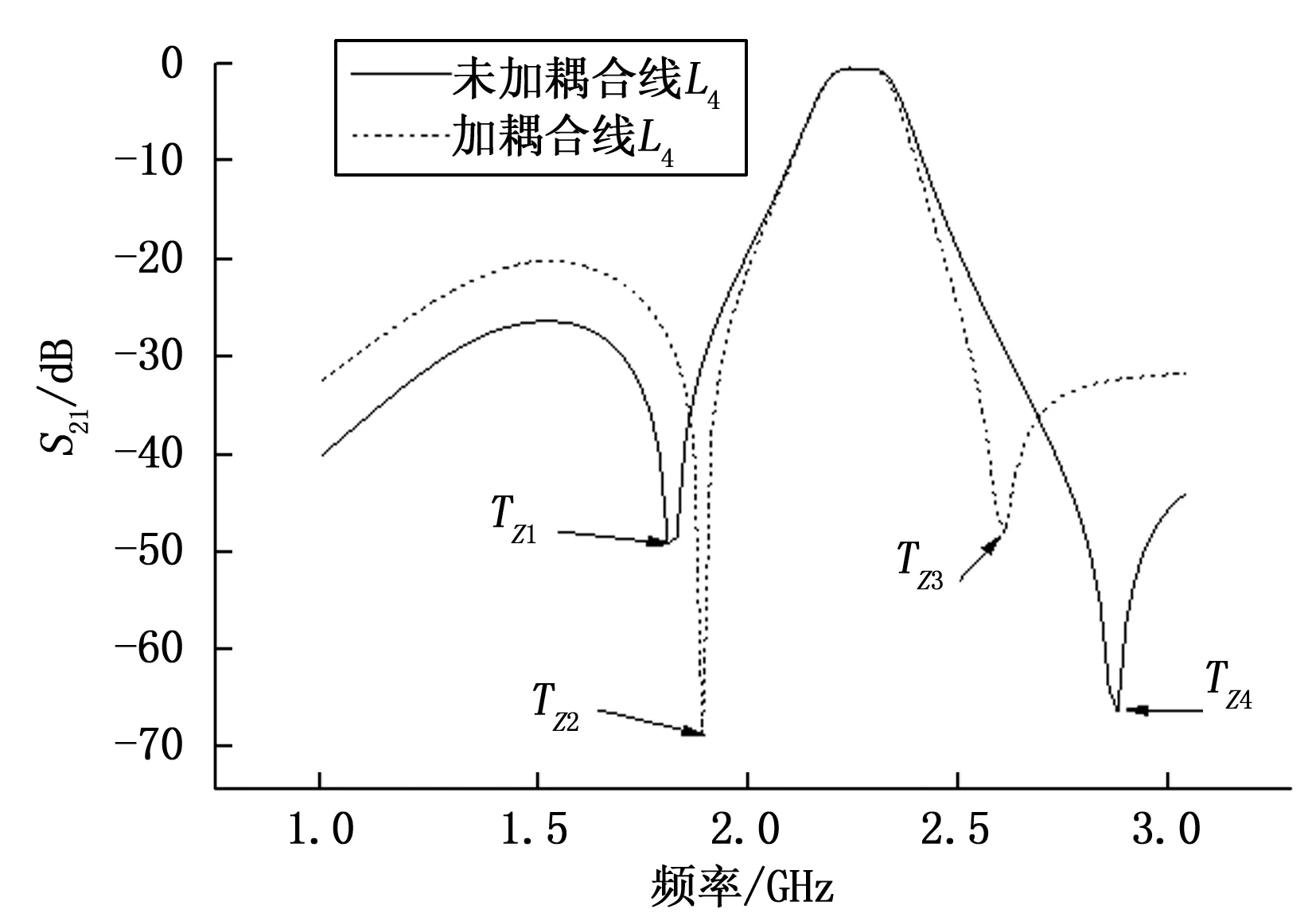
图7 添加耦合线的滤波器通带选择性的变化曲线

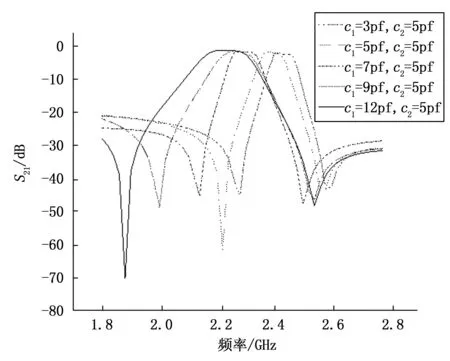
图8 枝节加载的电调滤波器S21参数曲线

仿真过程中，加载枝节L2端的变容二极管Cv2容值为5 pf，变容二极管用容性边界等效。由图8可知，随着谐振器端加载变容二极管容值Cv1的增大，滤波器的工作频率逐渐减小，变容二极管Cv1的可调范围为2～10 pf，超过该范围滤波器的带内和带外特性变差；滤波器的频率可调范围为2.10～2.40 GHz,频率变化范围为300 MHz。通过改变加载在谐振器的开路端和加载枝节端变容二极管的容值，实现了微波滤波器频率的电调，但该电调微波滤波器的带宽随着变容二极管容值的增大，带宽增大，即该电调滤波器实现了滤波器频率电调，但滤波器带宽不恒定。

由图8可知，该电调微波滤波器的阻带衰减不理想，下阻带最小衰减20 dB，上阻带的最小衰减为30 dB，不能满足微波滤波器的带外衰减要求，这主要是由于微带传输线谐振器的周期性。为了增大带外衰减，可通过在带外引入传输零点的方法。为了在带外引入传输零点，提出了一种新型的频变馈电结构，如图9所示。该馈电结构由输入输出耦合和源和负载耦合组成。输入输出耦合馈电结构采用平行线耦合馈电结构，包括电容c和一段接地短路线。该接地短路线由长度为L3的传输线和长度为L4的短路线构成，传输线L4实现输入输出耦合馈电。源和负载耦合结构由开路线构成，该开路线包括传输线L6、L7和L8，开路线之间的间距G3和L8决定带外传输零点的位置。因此滤波器整个耦合路径包括输入输出耦合路径和源和负载耦合路径，输入输出耦合路径为主耦合路径。当这两个耦合路径相位相反，幅度相等时，出现传输零点。图10为该新型频变馈电结构电调微波滤波器的传输特性仿真曲线。从图10可知，利用新型的频变馈电结构，在该电调滤波器的上阻带引入一个新的传输零点。与图8的曲线相比，该电调滤波器的上阻带和下阻带的衰减大于30 dB。因此引入该新型频变馈电结构不仅引入传输零点，也改善了滤波器的带外衰减特性。

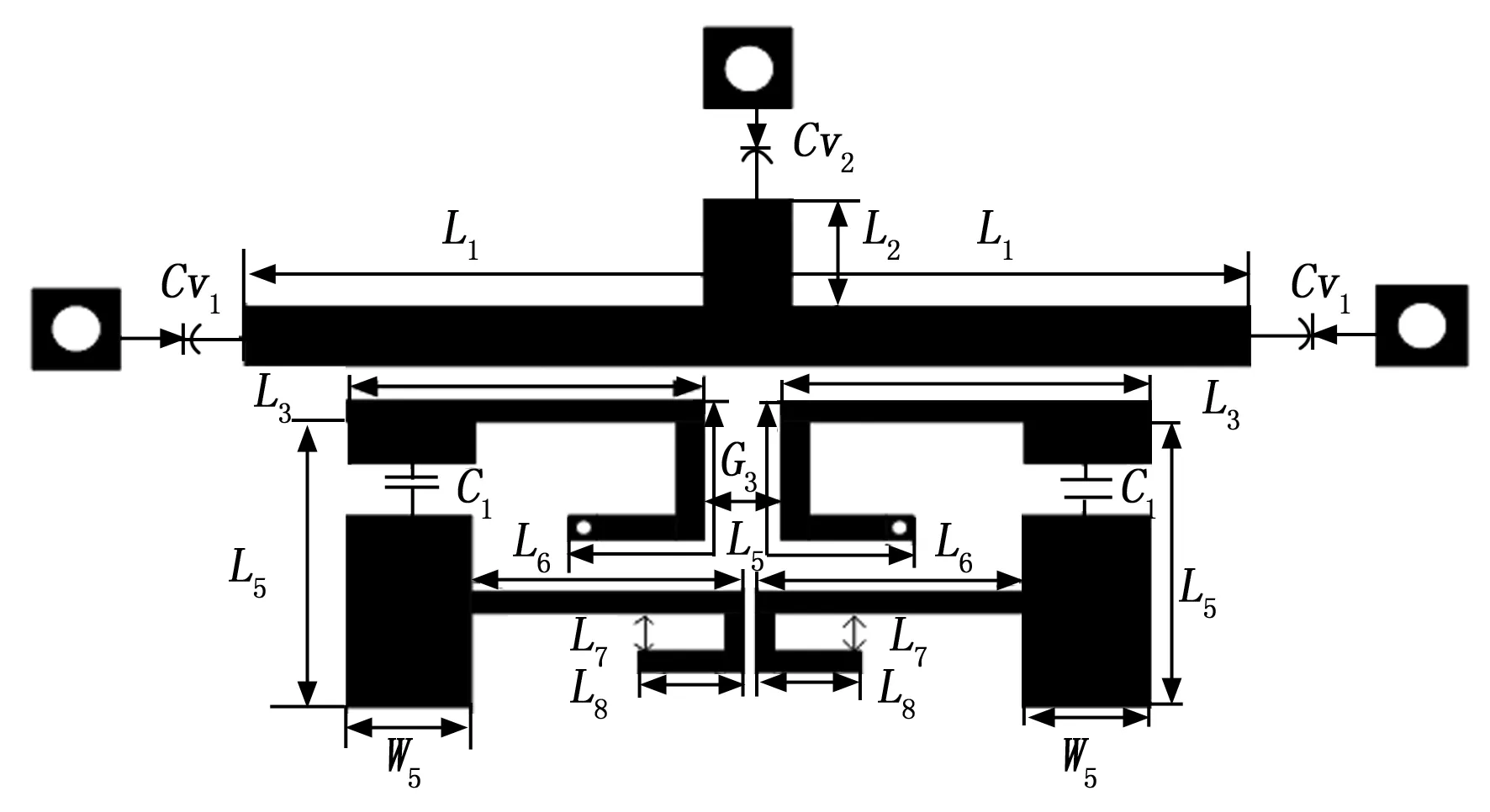
图9 新型频变馈电结构的电调微波滤波器

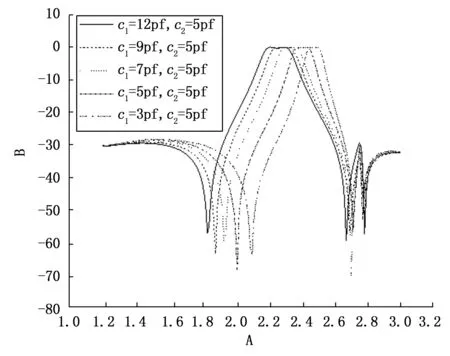
图10 新型频变馈电结构的电调微波滤波器S21参数曲线

4 结束语

本设计在分析枝节加载微带线多模谐振器的基础上，提出了一种频率可调谐振器，并利用该谐振器设计了一频率可调的微波电调滤波器，并实现了微波滤波器的小型化。通过仿真优化确定了滤波器几何尺寸，给出该滤波器的拓扑结构。从仿真结果可知，该微波滤波器可实现滤波器工作频率的电调，随着加载变容二极管容值的减小，滤波器的工作频率增大，带宽逐渐减小，未实现滤波器工作带宽的恒定。为了改善滤波器的阻带衰减特性，提出一种新型的频变馈电结构，有效改善了滤波器的带外衰减特性，并在上阻带引入了一新的传输零点。