钨空位捕获氢及其解离过程的分子动力学*

付宝勤 侯氢 汪俊 丘明杰 崔节超

(四川大学原子核科学技术研究所, 辐射物理及技术教育部重点实验室, 成都 610064)

氢(H)同位素滞留问题是聚变堆第一壁材料设计的关键, 而深入理解H在缺陷(如空位)处的非均匀形核长大过程有助于揭示H起泡及滞留的机制.针对第一壁材料钨(W)中空位捕获H及其解离的动力学过程开展研究, 通过耦合捕获和解离两过程, 构建新物理模型, 避免了原单一过程的物理模型需准确记录相应事件首次发生时间的不足, 另外新模型可同时提取解离系数和有效捕获半径等动力学参数.通过分子动力学模拟发现新模型能较好地描述W中空位-H复合体对H捕获和解离的动力学过程, 根据空位-H复合体随时间的演化曲线, 提取了有效捕获半径和解离系数等动力学参数.一方面能为动力学蒙特卡罗和速率理论等长时空尺度方法提供输入参数, 另一方面促进了分子动力学的发展, 进而实现了以较低计算资源获得更可靠的计算结果.

1 引 言

金属钨(W)以其具有优异性能(高熔点、高热导、高硬度、抗腐蚀和低溅射等)而被广泛应用于国防军事工业及核技术等领域, W基材料被认为是最具潜力的面对等离子体材料(plasma-facing material, PFM)[1,2].而作为 PFM的 W需承受等离子体辐照、高热负荷和中子辐照, 会引起复杂且不同尺度的损伤[3—6], 导致氢(H)同位素(包括氘(D)和氚(T))的滞留, 影响PFM的服役及燃料的自持, H同位素滞留问题是聚变堆第一壁材料设计的关键.W中H滞留受多种因素影响, 如：H的引入方式、温度、压力、材料的成分及结构等.在聚变堆偏离器区域, W将受到高束流密度(1022—1024m—2·s—1)的低能 (通常 ＜ 200 eV) D/T 辐照[7],该辐照也称为“亚临界”辐照, 即入射粒子能量小,不能直接使W阵点离位, 且对应射程只有几纳米[8].然而H滞留深度可超过微米[9,10], 这是因为H在W晶格中扩散势垒低[11—13], 且不能通过自捕获机制形成H团簇, 因而可快速迁移至表面层(指射程区域)以下的扩散层.然而H在W晶格中的平衡溶解度极低[12], 表明扩散层的H滞留主要受到材料本征缺陷或中子辐照诱导缺陷的影响.缺陷对H的持续捕获可能导致H泡(或称H团簇)的形核及长大, 因而对空位[14—16]、位错[17,18]和晶界[19,20]等缺陷处H泡非均匀形核机制的研究至关重要.虽然W中空位的平衡浓度低, 但是中子辐照引起离位损伤使材料中存在大量的过饱和空位[21], 这些空位的大小、分布及其演化直接影响W的性能及寿命, 因而深入理解H在空位处非均匀形核长大过程有助于揭示W中H起泡及滞留的机制.

W中H演化微观过程的实验研究极为困难,需借助多尺度方法研究.第一性原理[22]可计算小尺寸(指约100原子数的体系)缺陷结构的形成能,也可选定部分路径计算迁移势垒.分子动力学(molecular dynamics, MD)[23]可对大尺寸超胞 (如百万原子数的体系)开展计算, 且能研究动力学事件(一般指小于纳秒的过程), 获取动力学参数.动力学蒙特卡罗和速率理论可对更大尺寸体系研究更长时间的演化, 然而其结果的可靠性取决于输入参数的准确性.这些输入参数包括热力学参数和动力学参数, 可通过实验或计算(第一性原理/MD)获得.然而对于动力学参数, 实验上往往通过预设物理模型间接外推, 难以准确直接测量, 又由于温度的影响, 动力学转变机制复杂多变, 所以需借助MD开展研究.

MD经过数十年的发展, 模拟技术已比较成熟, 当前MD模拟发展趋势主要是以更高的效率、模拟更大的体系、实现更长的演化时间、取得更精确的结果[24].本课题组前期已自主开发了GPU并行加速的分子动力学软件(MDPSCU), 实现了MD模拟从计算技术和算法上的发展[25]; 动力学过程的模拟是MD模拟的特色, 而提取动力学参数的物理模型还不完善, 需进一步发展.比如, 前期在计算有效捕获半径(ECR)时, 通过在一个超胞中引入多个H, 从而加速了超胞中空位捕获H事件的发生, 这也是提高MD模拟效率的重要方法[26];另外, 前期针对多路径转变(如双空位-H复合体(V2Hx+1)的 H 解离 (V2Hx+1→ V2Hx+ H)或空位解离 (V2Hx+1→ VHx+1+ V), 计算各路径的动力学参数时, 重构了物理模型, 给出了新公式, 以获取更精确的计算结果[27].然而前期推导的物理模型[26—28]均需准确记录相应动力学事件首次发生的时间, 否则会发生计算精度不足的问题, 为了解决这一问题, 本文通过耦合捕获与解离过程, 推导出新物理模型, 并针对W中空位捕获H及其解离的微观动力学过程开展MD研究, 验证了新模型的可靠性, 且新模型可同时提取有效捕获半径和解离系数等动力学参数.因而本文目的不仅是为动力学蒙特卡罗和速率理论长时空尺度方法提供输入参数, 同时也是要在方法上实现以较低计算资源获得可靠的物理参数, 这也是MD的重要发展方向.

2 物理模型与计算细节

2.1 物理模型

针对W中空位捕获H和解离H的两个单一动力学过程, 前期分别推导了提取有效捕获半径和解离系数的物理模型[26].其中有效捕获半径用以表征空位及空位-H复合体 (VHx,x=0,1,···)捕获溶质H原子的能力, 可等效为VHx与溶质H的反应距离[29], 因而捕获速率可表示为捕获H后的复合体(VHx+1)的浓度(CVHx+1)随时间(t)的变化率, 即

式中,Rc,x即 VHx对溶质 H 的有效捕获半径;DA(A= H或VHx)表示A的扩散系数, 而溶质H的扩散系数一般要比W空位大得多(即DH≫DV)[13,26],且空位-H复合体的可动性比空位更低[30], 因而DVHx在计算过程中可忽略.另外根据体积为V的超胞中A的数量(NA)与浓度(CA)的关系,NA=VCA, 则 (1)式可变换为

在 MD模拟初始时, 超胞中只创建一个VHx和M个溶质H原子, 如前所述, 这里设置M个H是为了加速捕获事件的发生, 但高浓度的溶质H将影响其扩散行为[31], 因而M不宜太大,前期研究[26]发现对于2000个W原子的体系,M取值为10时, 计算结果较为可靠, 受浓度影响可忽略.对于捕获过程的MD模拟, 只关注捕获事件 (VHx+ H → VHx+1), 那么对于超胞, 要么未发生捕获(存在一个VHx), 要么已发生捕获(存在一个VHx+1), 对于已发生捕获的超胞将停止运行, 且认为该超胞中在后续时间都存在已捕获溶质H的VHx+1.进行Nb次模拟, 即针对Nb个超胞开展MD模拟, 每个超胞设置不同随机数种子(溶质H的位置也随机设置).假定Nt,x+1表示t时刻已发生捕获事件的超胞数, 可相当于含有VHx+1的数量, 则(2)式可变换为

对(3)式进行积分, 可得

因而VHx对溶质H的有效捕获半径(Rc,x)可通过 ln(Nb—Nt,x+1)-t曲线的斜率推导获得.类似上述推导过程, 可推导出空位-H复合体(VHx+1)解离H过程的物理模型[26—28], 假定该动力学过程为一级反应, 则

式中kdiss,x+1为解离系数, 表征上述事件发生的快慢.同样进行Nb次模拟, 每个超胞初始时仅含有一个VHx+1, 这儿Nt,x+1可表示为t时刻未曾发生解离事件的超胞数, 则

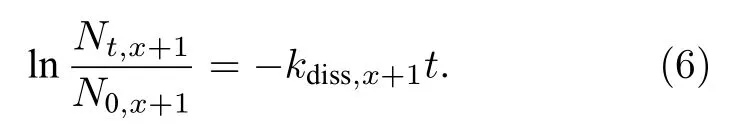
因而 VHx+1的解离系数 (kdiss,x+1)可通过ln(Nt,x+1)-t曲线的斜率推导获得.基于上述两单一过程的物理模型, 前期对W中空位/双空位-H复合体(V1/2Hx)捕获H及其解离动力学过程进行了研究[26,27].

上述物理模型均要求准确记录已发生相应事件的时间, 然而MD模拟过程中一般间隔一定时间(或步数)输出超胞的构型(包括原子坐标、速度和受力等信息), 通过分析构型中是否存在空位-H复合体(VHx+1)来判定相应事件是否已发生.该处理方法可能存在误差, 比如, 对于捕获过程, 在某间隔时间内, 某超胞可能连续发生捕获和解离的事件, 从而在输出构型时, 并未鉴别出该超胞已发生过捕获事件.解决方法之一是缩短输出构型的时间间隔, 然而该方法将增大数据的存储负担; 第二种方法是在线分析法, 该方法不需输出构型, 而是直接在MD模拟过程中一边计算一边分析, 然而该方法将增加计算时间, 尤其是对于GPU并行计算, 往往存在不同内存之间的数据拷贝, 影响并行效率, 另外该方法还不利于非预设的数据处理.事实上最好的方法是通过改进物理模型来防止上述误差的产生.记录的参数在新模型中应只与当前构型有关, 而不是还与之前的构型有关.可耦合捕获与解离两基本动力学过程, 构建新模型以避免上述不足.下面以解离过程为例推导, 假定MD模拟初始时, 超胞中只含有VHx+1, MD运行过程中存在H的解离, 同时也可能存在解离H的再捕获, 那么根据(1)和(5) 式可知

(7)式已忽略了相比溶质H扩散系数(DH)较小的DVHx+1, 乘以超胞体积(V)可得

式中nVHx和nH特指单个超胞中VHx和溶质H的数量, 若进行Nb次独立的MD模拟, 则

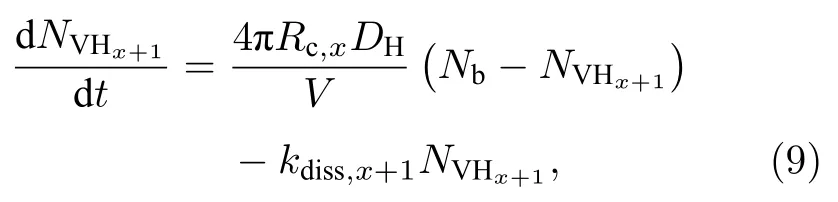
(10)式定义了

因而基于(10)式, 相应过程的解离系数(甚至包括其逆过程的有效捕获半径)可通过拟合yVHx+1(t)-t曲线推导获得, 这里 VHx+1的比率yVHx+1(t)=NVHx+1(t)/Nb仅与t时刻的输出构型有关, 因而新模型原则上可获得更精确的动力学参数.根据y-t曲线拟合的参数p与q, 解离系数(kdiss,x+1)和有效捕获半径(Rc,x)可得

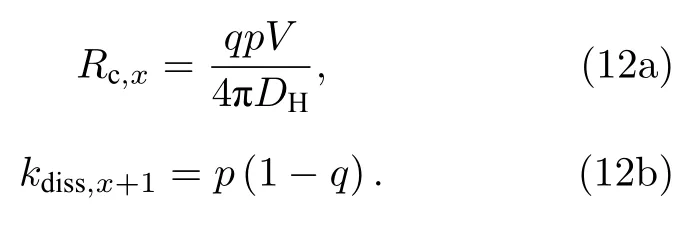
2.2 计算细节

本文针对W中空位捕获H及其解离过程开展MD模拟, 并基于新物理模型拟合方程, 提取有效捕获半径和解离系数等动力学参数, 这儿选用Bonny等[32]拟合的W-H嵌入原子势函数(EAM1),时间步长选用 0.2 fs, 使用速度-Verlet算法[33]来求解原子的运动方程.W一般为体心立方(BCC)结构[34], 超胞大小为 10a× 10a× 10a, 其中a为BCC-W 的晶胞参数 (a= 3.14 Å[35]),x,y,z取向分别为 [100], [010]和 [001], 均使用周期性边界条件, 完美超胞含有2000个W原子, 超胞尺寸足以消除点缺陷之间的相互作用, 可保证计算的可靠性.对于解离过程, 在超胞中心删除一个W原子以创建一个空位, 然后在空位中随机插入若干个H原子, 以构建空位-H复合体(VHx+1), 如图1所示, VH2位于超胞的中心, 该图原子的显示使用了OVITO软件[36].

图1 含有空位-H 复合体 (VH2)的初始超胞, 其中红色点表示W原子, 蓝色球表示H原子Fig.1.One simulation box with vacancy-H complex (VH2),where red pots represent W atoms and blue spheres represent H atoms.

MD模拟的基本过程与前期研究类似[37,38]：首先是将含有VHx+1的初始超胞进行原子位置局部最优化处理, 然后按麦克斯韦-玻尔兹曼分布设定原子速度热化超胞, 将超胞温度稳定至所需温度,再进行22 ps的自由演化, 此后进行正式的模拟且采集有效的数据, 在该阶段采用微正则(NVE)系综, 运行 100 万步 (即 200 ps), 超胞的瞬间构型每隔 2 万步 (即 4 ps)输出一次.在运行结束后, 对输出的构型进行原子位置局部最优化处理, 然后通过对比优化后的构型和完美点阵的Wigner-Seitz胞,判定超胞中是否存在空位-H复合体(VHx+1).对于捕获过程, 主要的不同是初始超胞的构建, 除了设置VHx, 还随机设置10个溶质H原子.

3 结果与讨论

3.1 解 离

对于解离过程, 初始超胞中只设置空位-H复合体(VHx+1), 在MD模拟过程, 会出现H的解离,当然也可能会出现解离后的溶质H被VHx重新捕获的情况.但根据新物理模型, 只要知道当前构型下空位-H复合体(VHx+1)的数量即可推导出相应过程的动力学参数, 而不必准确记录相应事件的首次发生时间.图2所示是不同类型的事件在不同温度下空位-H复合体(VHx+1)的比率(yVHx+1(t))随时间(t)的变化, 由图2可以发现MD模拟获得各输出时间点的VHx+1的比率(图2中点表示)能被新物理模型(图2中曲线表示)较好地拟合, 表明该模型可用于描述捕获和解离的耦合过程.

图2(a)—(f)主要用于研究解离过程, 即初始时超胞中只设置了空位-H复合体(VHx+1).根据拟合参数p与q以及(12b)式可获得解离系数(kdiss,x+1).另外若解离是热激活过程, 则解离系数可用Arrhenius关系来描述温度(T)的影响, 即

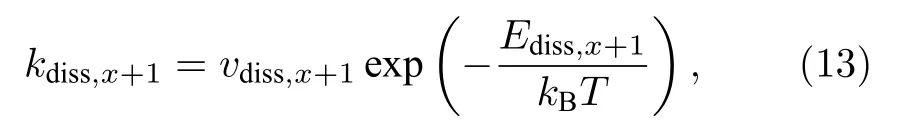
式中,νdiss,x+1是前因子, 一般认为与温度无关;Ediss,x+1是解离能, 表示空位-H复合体(VHx+1)的H解离形成溶质H的势垒;kB是玻尔兹曼常数.如图3所示, lnkdiss,x+1与1/T呈现较好的线性关系, 表明解离过程是个热激活过程, 因而可根据曲线截距和斜率推导出前因子和解离能.

新物理模型推导出的解离能在0.58—1.9 eV之间, 与第一性原理计算结果[30]接近.如图4(a)所示, 新模型推导的解离能(Enew)与前期单一过程物理模型给出的解离能(Eold)[26]比较接近, 表明两种模型在计算解离能时都比较合理, 另外从图4(a)还可发现空位-H复合体(VHx+1)的H解离能随捕获H的数量增加而减小, 该趋势也与前期结果[26]及第一性原理计算结果[30]一致.图4(b)是解离前因子的比较, 可以发现二者的接近程度不如解离能, 这主要是由于经过了指数的数学变换.事实上对lnν, 前后模型给出的数值也比较接近.另外由图4(b)还可以发现, 前因子粗略地随捕获H数量的增加而增加, 即粗略地随解离能的减小而增加.前因子的变化范围在 6—70 ps—1, 表明在一些计算中前系数被认为是常数(1013s—1)的假定是不合理的.

3.2 捕 获

图2 不同温度下, 空位-H 复合体 (VHx+1) 的含量 (yVHx+1(t)=NVHx+1(t)/Nb)与时间(t)的变化, 其中曲线由 (10)式拟合Fig.2.Ratio of VHx+1 in the simulation (yVHx+1(t)=NVHx+1(t)/Nb) as function of time (t), where the curves are fitted by Eq.(10).

如前文所述, 在研究空位-H复合体(VHx+1)解离过程时也可能存在解离H再被捕获的情况,而且根据(12a)式, 有效捕获半径(Rc,x)理应也能推导获得, 事实上通过解离过程拟合获得的Rc,x大多在 0.5—4 Å, 与前期[26]结果相近.然而应指出的是, 对于有效捕获半径的计算, MD模拟过程中应该保证有足够数量的捕获事件发生以满足统计学规律.如图2(a)所示的 2250 K 时 VH → V+H事件, 含有 VH超胞的比率 (yVH)几乎随时间(t)线性下降, 表明存在较少的捕获事件, 因而该y-t曲线不宜用来推导有效捕获半径, 类似的情况还有1500 K 时的 VH2→ VH+H 事件 (图2(b))、1000 K时的 VH3→VH2+H 事件 (图2(c))、1000 K 时的VH4→ VH3+H 事件 (图2(d))、500 K 时的 VH5→VH4+H 事件(图2(e))和700 K 时的VH6→ VH5+H 事件 (图2(f))等.另外对于 VH6→ VH5+H 事件, 由于解离能较低, 不易发生捕获事件, 因而对于800 K和900 K也不宜用于计算有效捕获半径.事实上, 前期事实上, 前期[26]在研究高捕获状态的空位-H复合体(如VH7)的解离过程时就发现, 在热化阶段绝大多数超胞中的(VHx+1)已发生解离,因而在后期MD演化过程中很难发生捕获事件.

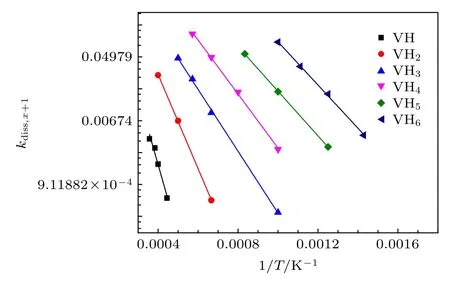
图3 不同空位-H 复合体 (VHx+1) 的 H 解离系数 (kdiss,x+1)与温度 (T)的变化, 其中曲线由公式 lnk = lnν — E/kB/T拟合Fig.3.Dissociation coefficients (kdiss,x+1) of H detrapping from various VHx+1 complex as functions of temperature(T), where the curves are fitted by equation lnk =lnν — E/kB/T.

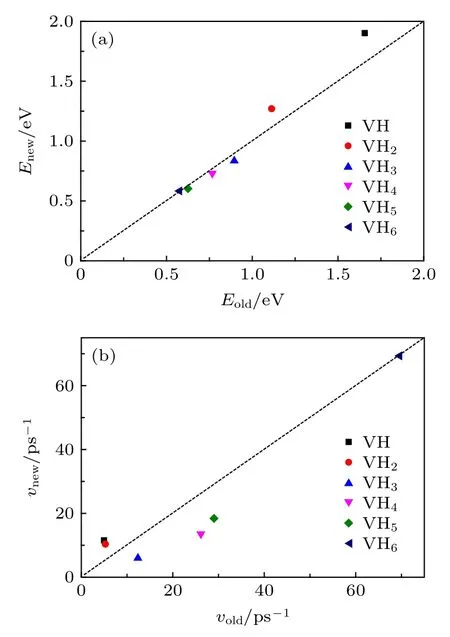
图4 新模型推导的解离能 (a)和前因子 (b)与前期模型[26]计算值的比较, 其中虚线表示 (Enew = Eold 或 νnew =νold)Fig.4.(a) Dissociation energies and (b) pre-exponential factors deduced by new model (present work) and old model [26], where the dash line means Enew = Eold or νnew = νold.

因而针对捕获过程, 在超胞中设置了VHx和溶质H原子, 增加捕获事件的发生.同样在MD模拟过程中, 溶质H原子可能会被VHx捕获, 捕获的H也可能再解离, 那么空位-H复合体的比率(yVHx+1(t))随时间(t)的变化关系仍可用(10)式来描述.图2(g)表示的是 V+H → VH 事件, 图2(h)表示的是VH+H → VH2事件, 可以发现MD模拟获得比率y(t)能被新物理模型较好地拟合, 同样表明新模型的可靠性, 根据拟合参数且运用(12a)式可推导出有效捕获半径.计算结果如图5所示, 新模型获得的有效捕获半径与单一过程物理模型[26]给出的结果比较接近.偏离较大的主要是高捕获状态的空位-H复合体(VHx), 这是因为这些复合体的解离能较低且存在较复杂的捕获与解离过程.另外由图5还可发现有效捕获半径在0.5—4 Å, 表明在一些计算中有效捕获半径被认为是一个晶格常数(3.14 Å)的假定可能并不合理.

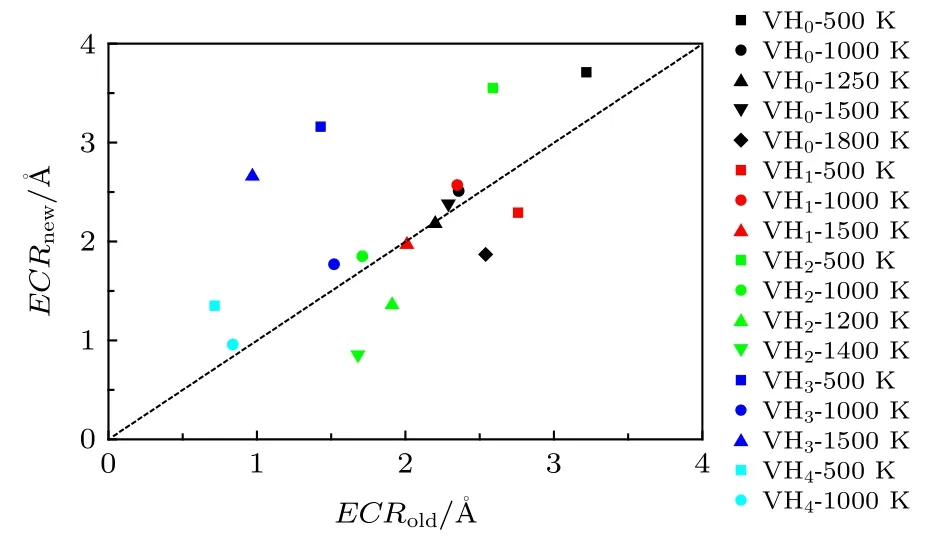
图5 新模型推导的有效捕获半径ECRnew与前期模型[26]ECRold 计算值的比较, 其中虚线表示 ECRnew = ECRoldFig.5.Effective capture radii deduced by new model(present work) and old model [26], where the dash line means ECRnew = ECRold.

4 结 论

由于单一过程提取动力学参数的物理模型需准确记录相应动力学事件首次发生的时间, 为了弥补这一不足, 本文通过耦合捕获与解离过程, 推导了新物理模型, 新模型通过不同时刻的瞬间构型,获得空位-H复合体(VHx+1)的比率与时间的关系,即可同时提取有效捕获半径和解离系数等动力学参数.针对W空位捕获H及其解离的微观动力学过程开展了MD研究, 验证了新模型的可靠性.提取了解离系数和有效捕获半径等动力学参数, 发现空位-H复合体(VHx+1)的H解离能随捕获H数量的增加而减小, 且解离前因子及有效捕获半径的数值较分散, 不应假定为常数.本文获取的动力学参数可为动力学蒙特卡罗和速率理论等长时空尺度方法提供输入参数, 同时本文推导的物理模型可实现以较低计算资源获得可靠的物理参数, 这也是MD的重要发展方向.