参考系波动下的参考系无关测量设备无关量子密钥分发协议*

谷文苑 赵尚弘 东晨 王星宇 杨鼎

1) (空军工程大学信息与导航学院, 西安 710077)

2) (密码科学技术国家重点实验室, 北京 100878)

3) (国防科技大学信息与通信学院, 西安 710006)

参考系无关测量设备无关量子密钥分发协议是解决实际系统中参考系对准问题的有效途径, 但其安全性的前提是参考系偏移速度缓慢.考虑到现实参考系波动和信号长度有限的情况, 重点讨论了参考系偏移和波动下的有偏基参考系无关测量设备无关量子密钥分发协议性能的有效性.仿真结果表明协议密钥率是关于偏移角的周期函数, 同时也是波动角的递减函数, 为下一步参考系无关测量设备无关量子密钥分发协议实用化打下了理论基础.

1 引 言

量子密钥分发 (quantum key distribution,QKD)是基于量子力学及基本定理的一种新型密钥体系[1,2], 以其绝对的安全性得到了广泛的研究,在理论研究和实验验证方面进展迅速[3-9].但现实设备和实验条件总是会与理想模型及假设存在一定差距, 这导致实际的QKD系统仍然存在许多安全性问题[10-16].2012年Lo等[17]提出了测量设备无关量子密钥分发 (measurement device independent quantum key distribution, MDI-QKD)协议, 在克服探测端全部安全漏洞的同时实现了协议性能的提升.近几年, 基于相位、偏振等编码方式的MDI-QKD演示实验已经相继完成[18-20].然而, 无论采用何种编码方式, 通信双方都需确立共享参考系以保证MDI-QKD系统有效的Bell测量, 但同时多参考系之间的校准会增加MDI-QKD系统的复杂性, 甚至可能产生信息泄露, 对系统安全产生威胁.

2014年, Yin等[21]提出了参考系无关测量设备无关量子密钥分发(reference frame independent measurement device independent quantum key distribution, RFI-MDI-QKD)协议, 有效地解决了参考系校准的问题, 并实现了系统性能在参考系缓慢偏移情况下的稳定性.然而, 已有研究表明统计波动下的RFI-MDI-QKD协议不再具有对参考系偏差的鲁棒性, 会随偏差角的增大产生性能衰减, 但这些分析都只是选取固定的参考系偏差角度进行分析, 并未涉及一般化情况, 且没有考虑参考系波动的情况[22-26].在实际环境中, 参考系偏差角会在一定范围内产生波动, 虽然文献[27, 28]已经讨论分析了参考系波动对参考系无关QKD协议 (reference frame independent quantum key distribution, RFI-QKD)的影响, 但仍然缺乏对参考系波动下RFI-MDI-QKD协议的性能分析.

本文主要研究了参考系波动下RFI-MDIQKD协议的性能.考虑到实际参考系波动的问题和有限长效应, 通过公式推导和仿真分析, 得到了参考系偏移角和波动角与有偏基RFI-MDI-QKD协议相关参数间的关系.仿真结果表明, 协议的性能与参考系偏差的角度密切相关, 并且其密钥率随参考系偏移角产生周期性波动, 随参考系波动角的增大而减小.

2 理论与模型

2.1 有偏基RFI-MDI-QKD模型

以偏振编码为例, 在诱骗态RFI-MDI-QKD协议中, Alice 和 Bob 使用三组共轭基{Z,X,Y}对量子态进行编码.协议假设Alice和Bob的Z基完全对准, 而两者的X基和Y基可以存在β角的偏差, Alice和Bob的三组基具体的关系如下[22-26]：

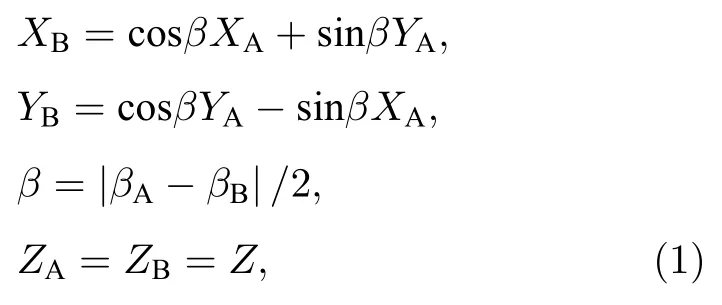
式中βA(B)代表着Alice和Bob的X基和Y基偏离标准参考系的角度.此时,和构成Z基,分别构成X基和Y基.其中Z基主要用于密钥的产生,X基和Y基的测量结果主要用于估计限制Eve获取的信息量的参数C.在渐近极限情况下,RFI-MDI-QKD协议具备对参考系偏差的鲁棒性,而现实情况下信号脉冲长度总是有限的.

为缓解有限长效应对RFI-MDI-QKD协议的影响, 文献[29]提出了有偏基RFI-MDI-QKD协议以产生更高的密钥率.该协议与原始诱骗态RFI-MDI-QKD协议不同点在于：原始诱骗态RFI-MDI-QKD 协议Z,X,Y基编码的信号态和诱骗态的平均光子数是相同的, 而有偏基RFIMDI-QKD协议的量子态有三种强度, 即信号态µ、诱骗态ν、真空态ω, 其中Z基下Alice和Bob只准备信号态µ,X和Y基下随机准备信号态µ和诱骗态ν.因此, 有偏基RFI-MDI-QKD协议密钥率的计算公式为[29]

且C值在 0—2 内取值,C值越小,IE越大.参数C与不同编码基下的增益和误码率有关, 这些测量结果满足[24]

2.2 参考系偏移和波动下的有偏基RFIMDI-QKD模型

如图1所示, 在实际不稳定的环境中, 由于相对运动和平台抖动, 通信双方共享的参考系总是会发生偏移且产生波动, 即Alice和Bob间的参考系方向夹角β不再是一个固定的值, 而是在一定的范围内变化、波动[27,28], 即 [θ-δ,θ+δ] .

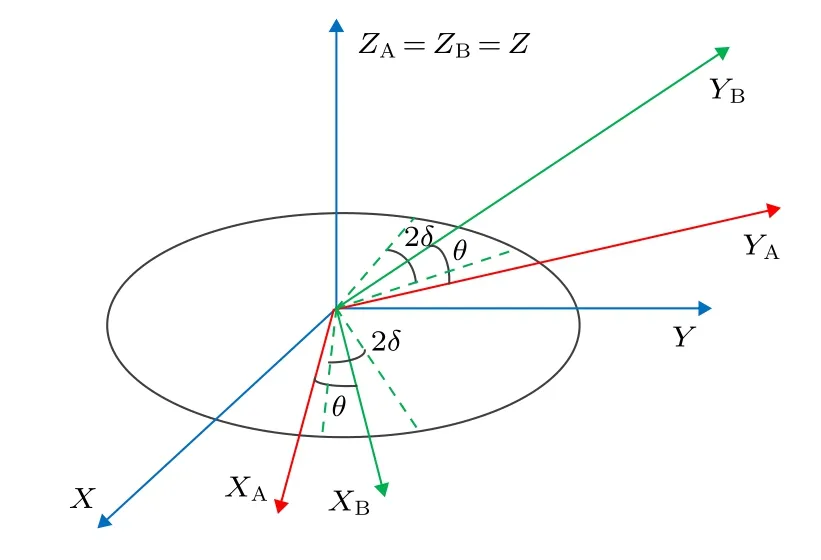
图1 Alice 和 Bob 的三组共轭基的实际位置关系图Fig.1.Relationship among reference frames of Alice and Bob.

文献[27, 28]通过在波动范围进行积分详细讨论了参考系偏移角和波动角与RFI-QKD协议性能间的关系.本文将此扩展到二维, 采用相同的方法来分析参考系波动下的有偏基RFI-QKD协议的性能.将参考系偏差β=[θ-δ,θ+δ] 代入求积分可得

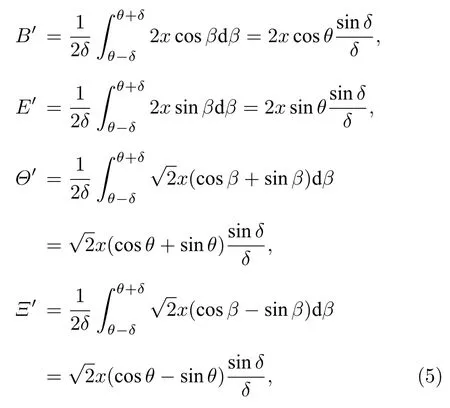
其中θ为参考系偏移的角度,δ为参考系波动的角度, 假设它们的取值范围均为 [ 0°,90°] .将(5)式代入(1)—(4)式, 可以求得参考系波动下有偏基RFI-MDI-QKD协议C值和密钥率R的关系式.

3 仿真与分析

考虑到实际信号脉冲的数量有限的实际情况,根据上述推导的公式可以得到参考系偏移角θ和波动角δ与有偏基RFI-MDI-QKD协议的参数C和密钥率R的关系.为方便比较, 固定协议的传输距离为20 km, 并假设切尔诺夫界失败的概率为ε=10-10, 脉冲总数为N=3×1012, 纠错 (隐私放大)失败的概率为表1列出了该协议其他的仿真参数[24-26].

表1 有偏基 RFI-MDI-QKD 协议的主要仿真参数Table 1.List of parameters of RFI-MDI-QKD with biased bases in the simulation.

图2显示了参考系偏移和波动下有偏基RFIMDI-QKD协议的C值变化.由图2(a)可知：当固定波动角δ时,C值为偏移角θ的最小周期为 π /2 的函 数, 而 且 在 [ 0°,90°] 范 围 内 存 在C(π/4+θ)=C(π/4-θ); 当改变波动角δ时,C值随波动角δ增大而减小.图2(b)则显示了有偏基诱骗态RFIMDI-QKD协议C值与波动角δ的关系.当固定偏移角θ时,C值与图2(a)曲线趋势相同, 这说明波动角δ越大, 窃听者可能窃取的信息IE就越多; 当改变偏移角θ时, 可以注意到曲线θ=40°与曲线θ=70°完全重合, 这是因为C值是关于偏移角θ的对称轴为 π /4 的周期函数.

图3为有偏基RFI-MDI-QKD协议密钥率R与偏移角θ、波动角δ的三维关系图.由图3可知, 该协议的密钥率R会随偏移角θ、波动角δ变化而发生变化.其中, 密钥率R随偏移角θ呈周期性变化, 并且变化范围较小, 而波动角δ对密钥率R的影响较大.图4(a)和图4(b)分别是有偏基RFI-MDI-QKD协议密钥率R与偏移角θ、波动角δ的关系图.由图4可知, 由于密钥率R与描述窃听者获取的信息IE的参数C有关,R随偏移角θ、波动角δ变化的趋势与参数C相同, 即密钥率R是关于偏移角θ的周期为 π /2 且对称轴为 π /4 的函数, 同时也是波动角δ的递减函数.可以注意到当偏移角θ接近 2 2.5°(67.5°) 时,R会随波动角δ的增大而产生骤减, 这是因为 2 2.5°(67.5°) 对应于密钥率R关于偏移角θ的函数谷值, 所以当δ较大时,协议性能会迅速下降.

图2 参考系偏移和波动下有偏基 RFI-MDI-QKD 协议的 C 值 (a) 参数 C 与偏移角 θ 的关系图; (b) 参数 C 与波动角 δ 的关系图Fig.2.Parameter C of RFI-MDI-QKD with biased bases under reference frame deviation and fluctuation：(a) The parameter C vs.the reference frame deviation θ ; (b) the parameter C vs.the reference frame fluctuation δ .

图3 有偏基 RFI-MDI-QKD 协议密钥率 R 与偏移角 、波动角 δ 的关系图Fig.3.Secure key rates R of RFI-MDI-QKD with biased bases in regard to the reference frame deviation θ and fluctuation δ .

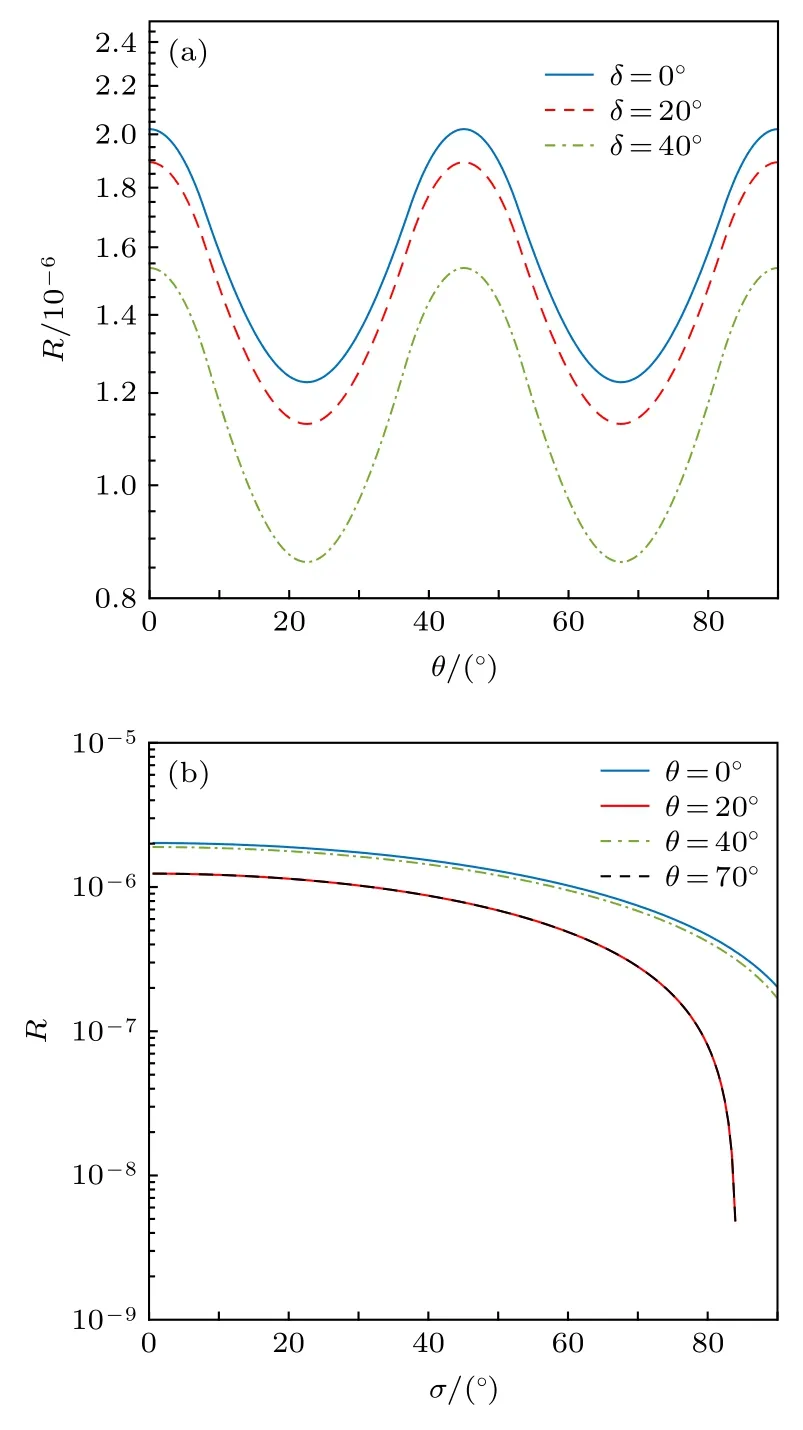
图4 参考系偏移和波动下有偏基RFI-MDI-QKD协议密钥率变化图 (a) 密钥率 R 与偏移角 θ 的关系图; (b) 协议密钥率R与波动角 δ 的关系图Fig.4.Secure key rates of RFI-MDI-QKD with biased bases under reference frame deviation and fluctuation：(a) The secure key rates R vs.the reference frame deviation θ ;(b) the secure key rates R vs.the reference frame fluctuation δ .

4 结 论

为解决MDI-QKD系统参考系需校准的问题,本文重点研究了有偏基RFI-MDI-QKD协议.针对现实环境中参考系波动的问题并考虑到有限长效应的情况, 分析了参考系偏移和抖动下有偏基RFI-MDI-QKD协议的有效性, 并分别讨论了参考系偏移角θ和波动角δ与协议参数C及密钥率R间的关系.仿真结果表明参数C和密钥率R均为关于偏移角θ的最小周期为 π /2 且对称轴为 π/4的函数, 同时也是波动角δ的递减函数, 为下一步RFI-MDI-QKD协议实用化打下了理论基础.