基于Black-Litterman模型对我国股票市场的资产配置研究
2019-12-16赵心
赵心

摘 要:本文基于Black桳itterman框架以上证50的股票数据为基础,运用ARMA桮ARCH模将投资者主观观点与资产的先验收益相结合,进而通过实证可以得出BL模型的预期收益普遍高于市场的均衡收益,在此基础上确认不同收益率下的投资组合权重,得到投资组合的有效前沿以及不同资产配置下的夏普比率,为投资者决策提供参考。
关键词:投资组合;资产配置;B-L模型
一、 引言
马科维茨的均值――方差模型是最早的投资组合理论,但令人遗憾的是,均值――方差模型虽然在数学上非常直观明了,但在投资实务中却存在着模型的输入参数期望收益率异常敏感的问题。为解决这一问题,1992年高盛的Fischer 和Robert 提出了Black桳itterman资产配置模型(简称BL模型)。该模型分别输出投资者对资产的观点和市场的均衡收益,根据贝叶斯方法将先验的收益和观点结合,得到后验的预期收益,求解二次规划得到最优的资产配置权重。
对BL模型的研究主要集中在观点收益向量和观点误差矩阵的预测。如温琪,陈敏等人基于GIR桮ARCH模型来预测收益率和方差;闫亚萍将美林“投资时钟”和BL模型相结合以及殷鑫鑫将风格轮动和BL模型相结合进行资产配置。本文基于贾慧提出的ARMA桮ARCH模型,通过GARCH模型输出的预期收益来代表投资者观点,协方差代表观点误差矩阵,代入BL模型求出后验收益率,与市场的均衡收益率进行比较的同时求解二次规划得到最优的投资组合权重。
二、 基于ARMA桮ARCH模型的实证分析
1.数据选取与检验
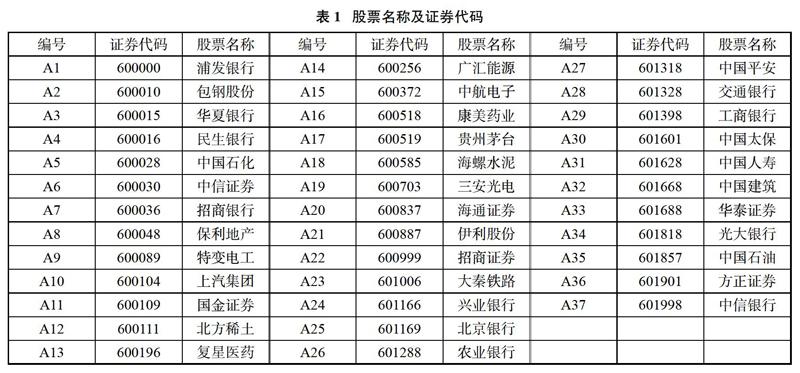
(1)数据选取。本文从上证50的50支成分股剔除了13支数据缺失较大的股票,最终留下37只股票(周收益率),数据来源于WIND.数据区间为2014年1月10日至2018年12月28日,贯穿了一个牛熊的轮回,经历了较为完整的市场周期,可以较全面的反应沪市的波动率特征。具体的股票选择情况如表1所示。
(2)描述性分析。基于周收益率,我们分别绘制了37只股票的时序图和QQ图.限于篇幅,暂且省略了相关图表,根据时序图的描述结果可得各股票收益率序列呈现出一定的波动集聚性,大的波动后面跟着小的波动.由QQ图可以得到各股票周收益率不服从正态分布,且尾部的散点偏离直线较明显,显示出厚尾特征。
对上证50的37只股票的描述性统计可以得出各股票周收益率序列的峰度普遍大于3,偏度均异于0,呈现右偏或左偏的分布现象;JB统计量均在1%的显著性水平下大于0,说明收益率序列不服从正态分布。
(3)平稳性检验。基于R语言,本文对37只股票的周收益序列进行平稳性检验(滞后12阶)。结果显示各股票周收益率序列的ADF统计量均5%显著水平下的数值,P值均小于0.01,故拒绝存在单位根的原假设,即各股票周收益率序列为平稳序列。
(4)相关性检验。对所选股票进行相关性检验,以A1桝4为例。A2的自相关系数存在着部分超出两倍的估计标准范围,A1、A3和A4除个别自相关系数触及两倍的标准线外,大部分落在两倍的估计标准范圍内,同时结合Ljung桞ox检验的Q统计量和对应的P值,可以得出A2的周收益率序列存在显著的前后相关性,A1、A3和A4的相关性较弱。
2.GARCH模型的实证分析
(1)ARMA模型及白噪声的建立。基于上述股票周收益率序列的相关性,本节建立ARMA模型。以A2和A3为例。我们对A2建立ARMA模型,根据拟合效果,ARMA(3,2)的系数高度显著,AIC和SC准则的值相比之下也是较小的。模型拟合结果为:
通过残差平方序列自相关检验,我们可以得到,A2的自相关图出现了“拖尾”现象,初步判断存在ARCH效应。为避免疏忽,对上述模型采用ARCH桳M检验,检验得LM统计量为32.073,对应的P值为0.00138。因此原序列存在ARCH效应,与自相关检验的结论一致。
基于A3的不相关性,将均值方程设定为白噪声,同时对A3周收益率序列的残差平方进行相关性检验。设立模型为:
根据所描绘的残差平方的自相关图可以看出A3残差的平方序列存在自相关。LM统计量为43.65,对应的P值为0.00001752,存在很强的ARCH效应。
(2)建立GARCH模型。由于上述残差序列均存在条件异方差,因此考虑建立GARCH模型来消除异方差。我们可以得到A2和A3的GARCH模型方程:
对拟合后的模型进行条件异方差检验,结果如表3所示,可以看出两个股票对应的F统计量和LM统计量所对应的伴随概率P值均显著大于0.1,表明其接受不存在ARCH效应的原假设。
用类似的方法,我们可以得到本文37只股票的残差序列均存在ARCH效应,对其分别建立GARCH模型均可消除其条件异方差性,得到37只股票的周收益率情况和条件方差作为BL模型的输入参数。
3.Black―Litterman模型构建与实证分析
(1)BL模型简介。BL模型的构建是先基于超额收益的协方差矩阵∑,流通市值权重,以及风险厌恶系数,得出均衡投资组合的隐含收益率∏,进而得出先验的均衡收益分布;基于观点向量Q和投资人观点误差矩阵 ,得到我们的观点收益分布。将二者相结合,基于贝叶斯方法我们可以得到预期收益:
将求解出的预期收益率代入到下面的均值方差模型中,求解最大效用:
通过逆最优化求解二次规划,得到我们想要的投资组合权重。
(2)市场均衡收益。首先基于∏= ∑求解我们的均衡收益,其中风险厌恶系数由公式 =来计算,和分别代表市场收益率和无风险收益率, 2是市场收益率的方差。本文以2014?018年同时期的50指数的周收益率和方差来计算,用十年期国债的收益率3.13%来表示无风险利率。由于2014年股市的波动,我们调整了14年股市的收益率权重,最终算出的风险厌恶系数 =3.48。进而代入公式求解出我们的市场均衡收益。结果如下:
(3)观点收益向量和观点误差矩阵。基于GARCH模型预测的周收益率和上述市场的无风险利率,我们可以得出超额收益率=输出观点收益向量Q,结果如下:
观点误差矩阵 基于GARCH模型求出的条件方差来表示。
(4)主观观点矩阵和信心水平。主观观点矩阵P通常有两种形式,相对观点和绝对观点。本文简化起见,采用绝对观点,以37阶单位矩阵来代表投资者对每只股票的观点。标量 代表投资者对所持观点的信心程度。本文采用Idzorek等人的观点,分别选取了0.01、0.05、0.1进行对比分析,经过实证结分析可以得出随着信心水平的提高,各股票的预期收益随之上升,因此为了得出更理想的结果,本文最终选择 =0.01。
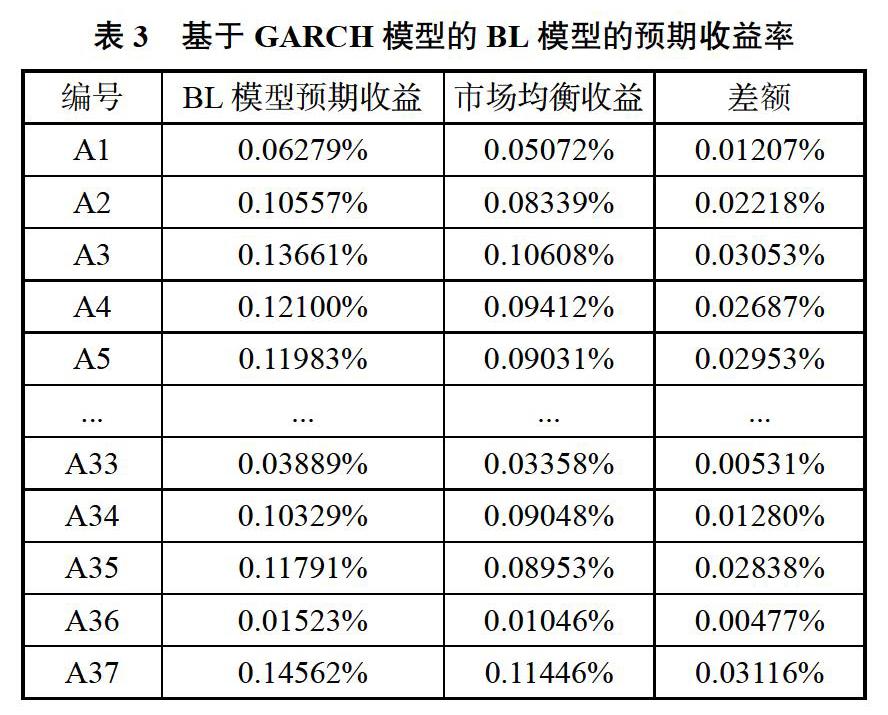
(5)BL模型预期收益率与最优投资组合。根据上述公式1中的预期收益E(R),将相关参数代入公式中,通过矩阵运算得出求解的BL模型的预期收益,如表3所示。
比较上表的BL模型预期收益和市场均衡收益我们可以看出,基于GARCH模型收益率和条件方差预测的收益率普遍高于市场收益率。与此同时,BL模型较均值方差模型而言,有效地避免了因个股收益的细微变动而产生的巨大变动,能够为投资者提供更加稳定的投资组合。
在这种情况下,我们基于预期收益率,通过调用R软件中的fportfolio包,我们计算得对应得投资组合得权重、协方差和在险价值。
由表4我们可以得出,对BL模型进行资产权重配置时,收益率为0.0013时,配置较为分散,重点配置在A1、A14、A35、A36;收益率为0.0036时,重点配置A7、A17、A25、A36;收益率继续上升时,股票权重配置的个数越来越少,收益率为0.006时,重点配置A7、A17两只股票;当收益率达到0.0083时,A17的配置权重达到了1。同样的观察协方差和在险价值,除了收益率为0.0011外,在收益率为正的情况下,我们可以看到,随着收益率的上升,协方差和在险价值也随之提高。符合我們的一般假定,收益越高,伴随的风险也越大。
在得到BL模型的预期收益率的情况下,我们基于R语言得到了投资组合的有效前沿。其中,中心区域的点代表着蒙特卡洛模拟的资产组合,与有效前沿相切的线代表着资产配置先,与之对应的中间的蓝点代表着等权重的资产组合,蓝色的曲线代表着不同投资组合的夏普比率。可以看出,当资产组合的目标收益率为大约0.003,风险最小为大约0.020时,当投资组合的目标收益率接近0.008时,投资组合的风险达到了0.0045。据此,结合投资组合的有效前沿和夏普比率线等,为投资者的风险投资决策提供参考。
三、结论
本文基于Black―Litterman模型的基础上提出了一个股票配置策略。选用ARMA―GARCH模型来拟合上证50的37只股票的收益率和波动率,将预测的收益率和波动率加入BL模型中,来计算投资组合的资产配置,并得到资产配置的有效前沿和夏普比率。研究结果表明:投资者信心水平的差异会造成BL模型的预期收益率向量有所不同,同时投资者的信心水平越大,BL模型的预期收益与市场均衡收益的差值越小,越接近市场均衡收益。另外,加入投资者观点的BL模型的预期收益率普遍高于市场的均衡收益率,随着收益的增加,投资组合会越发地集中于所选取股票池中的几只甚至一只股票。
参考文献
1.Black And Litterman.Global Portfolio Optimization. Journal of Fixed Income,1991.
2.贾慧.Black-Litterman模型在中国股票市场资产配置中的应用研究.西北大学,2011.
3.吴睿.Black-Litterman模型在证券资产配置中的应用研究.辽宁大学,2016.
(责任编辑:王文龙)
