Ho—Lee利率模型下DC型企业年金资产配置

蔡萍+常芳芳+孙海鹏

[摘要]近年来，随着人们对未来生活的要求逐渐提高，企业年金作为我国养老保障体系目标的第二支柱发挥着越来越重要的作用，近年来对企业年金的研究越来越深入。研究发现企业年金财富积累的关键在于企业年金的资产配置问题。文章假设无风险利率满足Ho-Lee利率模型，研究其对退休前DC型企业年金的资产配置的影响，建立并求解HJB方程，得到DC型企业年金资产配置的显式解。

[关键词]Ho-Lee利率模型；DC型企业年金；资产配置

[DOI]10.13939/j.cnki.zgsc.2017.02.064

1 引 言

我国的养老保险体系经过十几年的改革与发展，逐步建立起养老保险体系，其中企业年金作为我国养老保险体系的第二支柱在中国社会发展中对人们未来生活保障有着举足轻重的影响，因此对企业年金的研究显得尤为重要。按待遇给付对企业年金进行分类，企业年金主要分为两类：一类是确定收益型企业年金（DB型企业年金）；另一类是确定缴费型企业年金（DC型企业年金）。DC型企业年金领取者的未来收益由缴费额与企业年金投资收益的总和决定，并且成功地将投资风险转移给企业年金的领取者，因此我国建立的企业年金计划大多是DC型企业年金。Brison（1986）等研究发现，90%以上的投资收益取决于资产配置。因此，资产配置问题成了学者们研究的热点，本文在此基础上主要研究DC型企业年金保值增值的资产配置问题。

在DC型企业年金的资产配置的研究中，Boulier（2001），Cairns（2006）等假设风险资产价格的变化过程服从几何布朗运动，并假设无风险资产利率是一个常数，这显然与市场波动的不对称性不相符。由于企业年金投资期限较长，在投资期限内无风险利率并不是一成不变的，而是服从某个随机过程，因此以往的常数假设不能满足研究的需要。通过研究以及实证分析学者们提出了三种随机利率模型：Ho-Lee利率模型、Vasicek利率模型和CIR利率模型。随后随机利率模型被广泛应用于金融市场中资产价格的描述。Boulier（2001）等在利率服从Vasicek模型的假设下，利用鞅方法求解得到DC型养老金的资产配置问题的最优解。Cairns等假设利率服从Vasicek模型的描述，并将工资风险和资产风险考虑在内，研究了DC型养老金的最优资产配置问题。张初兵、荣喜民（2012）研究了CIR模型和Vasicek模型下DC型养老金的最优投资问题。常浩（2015）假定无风险利率服从Ho-Lee利率模型，并将其应用到多种风险资产的动态组合问题中，运用动态规划原理建立HJB方程，进而分析得到利率对资产的动态投资组合策略的影響。由此可以发现，随机利率对DC型企业年金的资产配置有重要的影响。

目前，对DC型企业年金资产配置的研究方法主要有两种：一是鞅方法，如Boulier（2001）等；二是随机控制方法，如Devolder（2003）等。之后，越来越多的学者将随机控制方法用于DC型企业年金资产配置的研究，如王力平（2014）等。由于企业年金持续时间较长，金融市场中无风险资产的价格变化在企业年金存续期间不是一成不变的，而是服从一定的利率模型。本文假定无风险资产的价格变化过程不再是一个常数，而是服从Ho-Lee利率模型，应用随机最优控制方法，以期末最大财富作为目标函数，建立HJB方程，通过一系列的求解得到HJB方程的显示解，进而得出Ho-Lee利率模型下DC型企业年金资产配置的比例。

2 模型建立

2.1 金融市场

由两基金分离定理，假设企业年金计划投资的金融市场中仅存在两种资产：一种是风险资产；另一种是无风险资产。以往的研究往往假定无风险利率为一个常数，本文在此基础上进行改进，改变了传统的常数假设，而假定无风险利率服从Ho-Lee利率模型。无风险资产的价格在t时刻记为S0（t），服从下面的微分方程：

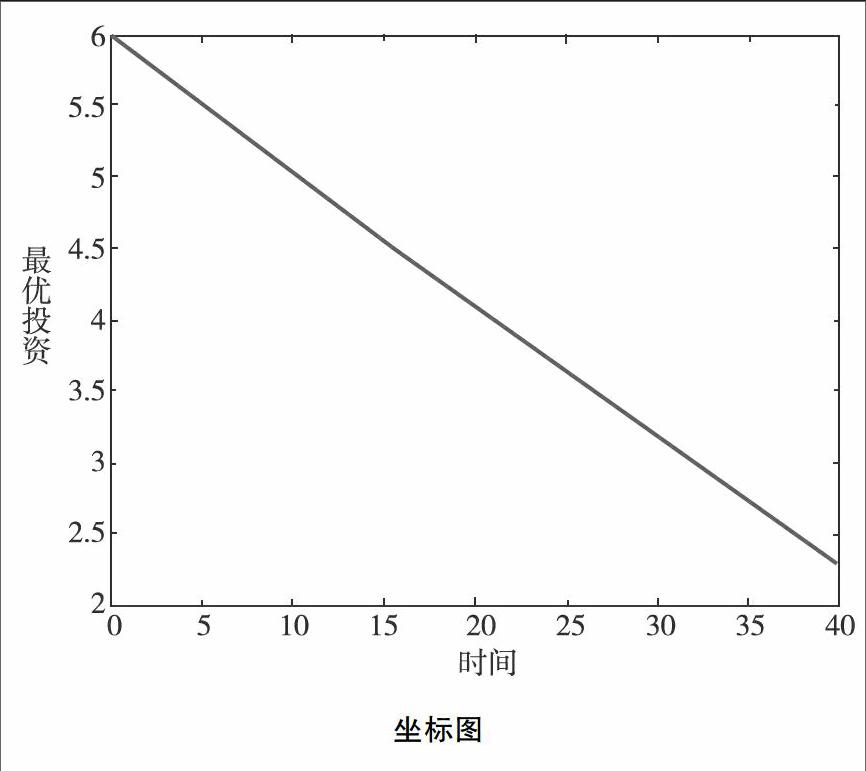
由下图可知随着时间的推移，企业年金领取者会逐步降低对风险资产的投资比例，进而加大无风险资产的投资。选取相对保守的投资策略给未来生活了提供了相应的保障。

坐标图

5 结 论

随着经济全球化的发展以及我国养老保险制度的完善，对企业年金的研究成了热点。而影响市场变化的因素也越来越多样性，面对这样的经济环境投资者进行投资时需要考虑的因素也越来越多。以往常数利率的假设已不再满足人们的需要，因此本文基于Ho-Lee利率模型对DC型企业年金的资产配置进行了研究。可以看出，Ho-Lee利率模型下DC型企业年金资产配置比例随时间的变化，给企业年金领取者提供了一定的理论依据，具有一定的应用价值。

参考文献：

[1] Brison G P，Gilbert B，Hood L R.Determinants of Portfolio Performance [J].Financial Analysts Journal，1986（42）： 39-48.

[2]Boulier J F，Huang S，Taillard G.Optimal Management under Stochastic Interest Rates： The Case of a Protected Defined Contribution Pension Fund[J]. Insurance： Mathematics and Economics，2001（28）：173-189.

[3]Cairns A J G，Blake D，Dowd K. Stochastic Lifestyling： Optimal Dynamic Asset Allocation for Defined Contribution Pension Plans[J].Journal of Economic Dynamics and Control，2006（30）： 843-877.

[4]张初兵，荣喜民.仿射利率模型下确定缴费型养老金的最优投资[J].系统工程理论与实践，2012，32（5）：1048-1056.

[5]常浩. Ho-Lee利率模型下多种风险资产的动态投资组合[J]. 数理统计与管理，2015，34（3）： 562-569.

[6] Devolder P，Bosch P M，Dominguez F I.Stochastic Optimal Control of Annuity Contracts [J].Insurance： Mathematics and Economics，2003，33（2）： 227-238.

[7]王力平，张元萍. 考虑死亡率的DC养老金资产配置研究的统一框架[J].保险研究，2014（4）：121-126.