知识生成要“少逼多悟”*
2019-12-11
(安丰中学,江苏 东台 224221)
1 提出问题
笔者有幸参加了“江苏省第14届中学数学教学高级论坛”活动,听取了江苏省江阴第一中学唐永老师的一节观摩课,课题是“曲线上一点处的切线”.唐老师的教学思路与苏教版《数学(选修2-2》)一致,课堂设计精巧,且唐老师教学功底深厚,令人折服.在评课环节中,江苏省南通市教研室的曾荣老师首先肯定了这节课,同时也指出这是一节很难上的课,这么多年来一直关注这节课,但始终未能听到一节很完美的课.那么这节课到底难在哪儿?到底应该怎么上才合理?为此,笔者做了一点探讨,当然未必能达到曾老师的要求,只是提出个人对该课应该怎么上的一点看法,与读者交流,以期抛砖引玉.
2 难点分析
教材先是指出平均变化率的含义,继而提出“如何精确地刻画曲线上某一点处的变化趋势呢”.该问题的提出有一定的合理性,意在由平均变化率过渡到瞬时变化率,即由割线的斜率过渡到切线的斜率.但学生很难理解“某一点处的变化趋势”这一似乎有点模糊的数学概念,他们更不知道“如何刻画”.正如曾荣老师所说,学生如果不预习,他们怎么能想到“放大曲线,以直代曲”的处理方法呢?因此,本节课的教学难点是切线斜率的生成教学,有了切线斜率的概念,求一些简单函数的切线方程不是问题.
如何突破这个教学难点呢?要“少逼多悟”.不要“逼”学生运用放大的处理手段,无论教师展示多完美的曲线的放大图片,都只是“逼”学生理解“曲线在某点附近逼近一条直线”.我们可以从学生已有的认知出发,引导他们“悟道”,悟出切线的一些要点,进而引导他们建立“曲线在某点处的切线”概念.至于“放大的处理手段,以直代曲的思想”,可作为切线概念生成之后的反馈.
3 教学设计分析
通过以上分析,笔者重新设计了这节课的教学思路,意在引导学生逐步认识“曲线上一点处的切线”的内涵,并通过简单问题的应用反馈切线的相关感知.
3.1 感知辨析
问题1今天这节课我们要研究“曲线在某点处的切线”这一问题.同学们在初中已经学习过圆的切线,知道“若圆心到直线的距离等于半径(或直线与圆只有一个交点),则直线与圆相切”.那么,是不是直线与曲线只有一个交点,直线就与曲线相切呢?
设计意图由熟知结论提出拓展问题,意在激发学生的探究欲望.

图1
由圆的切线导入新课,体现了由特殊到一般的研究思路,符合学生的认知规律.对于问题1,学生能想到直线与其他曲线的关系,尤其是他们非常熟悉的抛物线,如f(x)=x2.基础较好的学生会很快得到结论是否定的;其他学生经教师的点拨也都能理解这个否定性结论.如图1,直线l1,l2与抛物线f(x)=x2都只有一个交点,但直线l2不是抛物线f(x)=x2的切线,而直线l1是抛物线f(x)=x2的切线.虽然暂时还没有给出切线的严格定义,但是学生都能从图1中感知到这个否定性结论的合理性.
问题2我们已经发现,若直线与曲线只有一个交点,则直线与曲线未必相切.现在另一个问题是,如果直线是曲线的切线,那么直线与曲线一定只有一个交点吗?
设计意图提出逆向问题,让学生逐步感悟切线与曲线的关系.
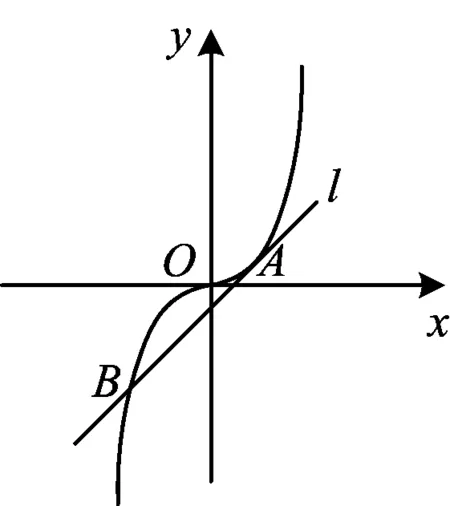
图2
虽然学生还不知道切线的严格定义,但他们能够凭直觉画出曲线在某点处的切线.对于问题2,学生容易不假思索地得到肯定性结论,教师应引导学生再研究直线与其他曲线的关系,给学生一定的思考时间,大多数学生最终能够想到直线与幂函数f(x)=x3的关系.如图2,直线l与f(x)=x3的图像相切于点A,但直线l与f(x)=x3的图像还有一个交点B.由此,学生得到关于问题2的否定性结论.
3.2 逐步深入
问题3在图1中,直线l1,l2与抛物线f(x)=x2分别有一个交点P,A,但这两个交点P,A似乎有所不同.同学们能不能说出这两个交点P,A的区别?
设计意图通过点的辨析,意在引导学生深入认识切线的本质.
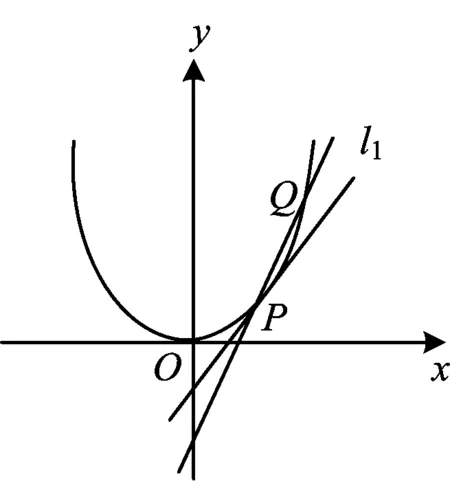
图3
问题3已初步触及切线的本质,先让学生辨析切点与非切点的区别.虽然学生还不知道切点的含义,但他们能感受到切点与非切点有所不同,只是难以言表.多给学生一些思考讨论的时间,总会有学生能说出其中的异同,再经教师的总结,可得到下列区别:直线l1与抛物线f(x)=x2的交点P好像是两个重合的交点,只要直线l1绕交点P稍微动一动,立即在其附近产生另一个交点;而直线l2与抛物线f(x)=x2的交点A就是一个交点,直线l2绕交点A稍微动一动,虽然也会产生另一个交点,但不是在点A附近(可以借助几何画板演示这里的区别).
3.3 本质揭示
问题4在图1中,直线l1绕交点P稍微动一动,立即在其附近产生另一个交点Q(如图3).假如给定P(x0,y0),能不能借助这样的运动来刻画直线l1的斜率?
设计意图通过直线的旋转,引导学生认识割线与切线的斜率关系.
学生当然不能直接得到直线l1的斜率,但他们会求直线PQ的斜率.由于点Q是点P附近的一点,可设Q(x0+Δx),f(x0+Δx)),从而
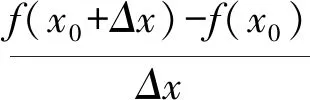
问题5在图3中,我们知道直线PQ的斜率体现了曲线在区间[x0,x0+Δx]上的平均变化率,那么切线l1的斜率体现了曲线在切点P处的什么特征?
设计意图进一步认识切线的斜率,从而让学生认识曲线在某一点处切线的内涵.
学生易推理出“切线的斜率体现了曲线在切点处的瞬时变化率”,但这个瞬时变化率比较抽象,还需要直观理解.于是,教师再追问:切线的斜率(即瞬时变化率)是曲线在切点处的一个数学量,它一定体现曲线在切点处的某种变化特征.我们需要充分观察切点处的这种变化特征、某一点处的变化特征(有点近似一种微观性质),基于这样的分析,学生可能会想到用放大的处理手段.如此,教师再用课件展示曲线在切点处逐步放大的图像.随着图像的放大,容易发现:在切点附近曲线与切线几乎重合,可以用切线代替曲线,切线的斜率(即曲线在切点处的瞬时变化率)体现了切线的走势也即曲线的走势.继续追问:在图1中,直线l2不是曲线的切线,如果逐步放大它们在交点A处的图像,最终得到什么图形?估计学生能够想到是两条近似的相交直线,然后再用课件展示放大的图像验证学生的想法.最后,教师再帮助学生总结归纳“以直代曲”的数学思想.
3.4 应用反馈
首先讲授课本例题:已知函数f(x)=x2,求曲线y=f(x)在x=2处的切线方程.目的是让学生再理解导数的概念,掌握求切线的基本步骤.其次补充讲解例题:已知函数f(x)=x3,求y=f(x)在x=1处的切线方程.不仅仅是加强理解与应用,还要利用该题反馈学生对问题2~4的感知认识.
学生能想到先求割线斜率
当Δx无限趋于0时,割线斜率
k=(1+Δx)2+(1+Δx)·1+12
无限趋于3,因此f(x)=x3在x=1处的切线斜率为3.又因为f(1)=1,所以f(x)=x3在x=1处的切线方程为y-1=3(x-1),即
y=3x-2.
由此,提出下列两个问题:
问题6在问题2中,我们感觉到曲线的切线除与曲线有一个交点是切点外,可能还有其他交点.能不能找到这样的函数呢?
设计意图让学生用实例验证问题2的结论,加深对切线的认知.

x3-3x+2=0,

x3-3x+2=(x-1)2(x+2),
因此方程有两个重根x=1,还有一个根x=-2.即函数f(x)=x3与其在x=1处的切线还有另一个交点(-2,-8),这说明我们对问题2的感知是正确的.
问题7在上述求交点的过程中,方程x3-3x+2=0的重根x=1刚好是切点的横坐标.同学们能不能解释重根对应切点的横坐标这一现象?
设计意图运用问题6的实例,从方程的角度,让学生进一步认识切点的含义.
问题7的目的是让学生再理解切线斜率的定义,再次感悟问题3和问题4.切点可近似地看成两个交点,如图3,对于割线PQ(点Q在点P附近),当点Q沿着曲线逐步逼近点P,割线PQ逐步逼近切线l1,切点P可认为是P,Q重合的点.可以想象,这样一条动态的直线与曲线联立方程组求交点,随着点Q沿着曲线逐步逼近点P,其中两组解就无限接近,消去y,得到关于x的一元方程的两根就无限接近,也即重根.
4 两点反思
对上文的教学设计,笔者谈两点个人看法,供读者参考.
1)创造性地使用教材.毫无疑问,教材是最科学、最严谨的教学资料.当然,教学不应唯命是从.陶行知先生曾讲过,教材无非是个例子.因此,我们要更新一个观点,教学不仅仅是教课本知识,更要教教师的思想和认知.创造性地使用教材,是指在遵循教学理念、遵循教材科学性的基础上,结合教师自身对知识的理解,合理设计教学内容、教学环节、教学问题等.况且,不同学校的生源差异很大,都千篇一律地照搬教材,显然不合适.我们应该因材施教,拥有优质生源的学校有必要适当拓展课本知识;而生源较差的学校适当删除一些内容,也应允许.
2)知识生成教学要“少逼多悟”.知识生成教学,是学生从无到有的接受过程,必须遵循学生的认知规律,循序渐进地引导学生发现问题、分析问题、解决问题,逐步构建新知识.知识生成教学应强调学生自然而然地接受,问题的提出不能突然,应在学生已有认知的基础上提出问题,他们才不排斥,才能积极主动地思考问题;问题的解决不能“逼”,否则容易造成学生思维断层、造成学生“假懂”.对于学生解决不了的问题,可不急于解决,可以从侧面引导、可举熟悉的例子让学生感悟,要尽可能让他们自己发现处理方法.当然,功夫在备课,要充分估计学生的能力,合理设计问题,才能减少教学中“逼”的现象.
