数学思维在解高考题中绽放*——兼评2019年浙江省数学高考第20题第2)小题

(台州市第一中学,浙江 台州 318000)

2019年的高考已落下帷幕，一些考生对浙江省数学高考试题表现出不适应，第20题第2)小题是“拦路虎”之一.此题到底考查了什么？难在何处？下面笔者就该题的思维过程进行剖析.

图1

题目如图1，已知点F(1,0)为抛物线y2=2px(其中p>0)的焦点．过点F的直线交抛物线于点A,B，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且点Q在点F的右侧，记△AFG,△CQG的面积分别为S1，S2．

1)略；

1 要谁——明确解题方向

评注俗话说：方向比努力更重要.解题的思路要向着目标，只有解题者明确了求解目标，才能知道该做什么.此题把面积问题化归为线段长或点坐标进行处理.解析几何有关线段、角、面积、定点等问题，往往通过设未知量建立方程，将几何问题转化为代数问题.这是解析几何的本质，也是高考解析几何解答题所要考查的核心内容.

2 设谁——合理选择变量

直线与圆锥曲线的位置关系常常要涉及到直线与曲线的公共点，对这些公共点处理妥当与否,关系到问题能否成功解决.本题若将△AFG,△CQG的面积用相关点的坐标进行表示，则如何求点G,Q,A,C的坐标？由于点C在抛物线上，△ABC的重心G在x轴上，这4个点的位置随直线AB变动而变动，那么如何表达直线AB的方程呢？这时需要解题者选择合适的直线方程形式.

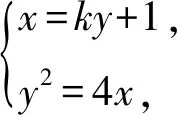
(1)

思路2若设A(t2,2t)(其中t≠0),则直线AB的方程为

(2)

3 有谁——挖掘几何特征

解析几何离不开图形，图形的几何特征是解题思维重要信息源，解题时要挖掘图形的几何特征，并从中提炼出有价值的数量关系.此题△ABC的重心G是最突出的几何特征，与面积相关的信息有什么？能否把△AFG,△CQG的面积转化到其他三角形中，而不需求点Q的坐标？

思路3因为G是△ABC的重心，所以△ABG与△ACG的面积相等.而

于是

又因为y1+y2=-yC，所以

(3)

笔者又思考：能否用三角形的边长表达这些三角形面积之间的关系？于是得到：

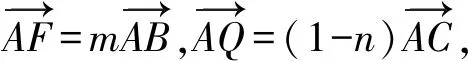
因为G是△ABC的重心，所以

又因为点F,G,Q共线，所以

4 舍谁——精打细算求简捷

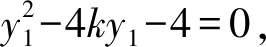
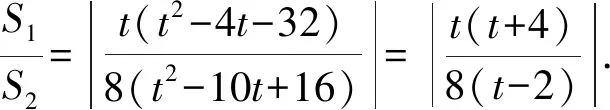
(4)

对于式(3)，多数考生根据y1y2=-4进行消元,得

若从式子结构看，分子、分母为齐二次形式，化简得

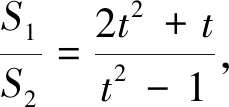
(5)

(6)

然后转化为求S的最小值.

评注消元是处理方程组常用的方法之一，根据解决问题的实际需要，消谁、留谁要进行分析、比较、抉择的，才能做到运算合理、简结、便捷.此题使用思路1的较多考生因消元思维受阻，导致解题无法继续往下做.由此可见，学生对含多个字母的代数式的运算能力比较薄弱，推理运算是解析几何的痛点.利用思路2、思路3解题不仅得分率要比思路1高，并且容易得高分，可惜人数较少.解析几何法不仅会列出等式,而且要列出“好式”，同时会有“好法”处理方程.本题最优的解法是深刻理解题意，充分发挥曲线的几何特征作用，抓住式子的结构特征，并灵活运用整体思想，做到对症下药,事半功倍.

5 用谁——因式施策求成效

求函数最值常用的方法有：利用导数知识、利用基本不等式公式、利用判别式.如何有效使用这些方法求函数最小值？由以上4种思路分别得式(4)，(2)，(5)，(6)，各式都可以利用导数进行求其最小值，但运算过程较繁.由于这4个式子虽然都是分式形式，但分子、分母最高次都是两次，因此都可化归为二次方程问题，利用判别式求其最小值.从考试实际情况来看，学生运用判别式方法求函数最值并不习惯，这表明学生缺乏灵活应用的能力，暴露出学生知识迁移能力较弱.对于式(4)，由于分母是关于t的一次形式,因此

评注高考不仅需要学生掌握扎实的基本知识、熟练的基本方法和技能，更需要对一题多解、一法多用加以概括和总结，才能对所学的知识和方法融会贯通，灵活运用.

6 建议

由以上剖析表明，高考解析几何解答题紧紧围绕解析几何的核心思想，在设变量、列等式、解方程、运算推理等各个环节中，考查数学思维能力.数学思维能力是在数学学习和应用的过程中逐步形成和发展的.因此，在解析几何教学中，建议做到以下3点：

1)重视数形结合能力的培养.解题先读懂图，即对图形变动性、依附性、特殊性等几何特征有一个初步的了解,然后挖掘其几何特征，找准曲线上的关键“点”，合理设参.

2)要用联系的视角审视题目中条件与条件、条件与结论之间的内在联系，正确把握解题方向.在选择参数和列方程时，要有全局意识，以“长远”的眼光建立“可靠”的等式,避免“后患无穷”.

3)重视学生数学学习能力的培养，倡导学会思考，自主提问，自我追问，在问题的探究和解决中深度思考，发展数学思维，优化思维品质.