常规题蕴涵能力深度 平凡法彰显素养水准*——2019年浙江高考卷解析几何试题解法探究与教学启示

(天水市第一中学,甘肃 天水 741000)

1 试题呈现

图1

题目如图1，已知点F(1,0)为抛物线y2=2px(其中p>0)的焦点，过点F的直线交抛物线于点A,B，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且Q在点F的右侧.记△AFG,△CQG的面积分别为S1,S2.

1)求p的值及抛物线的标准方程；

(2019年浙江省数学高考试题第21题)

2 题目表征

试题位于第21题，属于压轴题，主要担负高校人才选拔的区分作用，是一道值得肯定和研究的好题.下面笔者从试题背景、“4个”题设条件和“2个”解题目标的表征进行解读：

问题背景：开口向右的抛物线和直线的位置关系.

审视题设条件：

1)“焦点F(1,0)”表征：从纵、横坐标的正负和大小可知“该抛物线的开口方向(向右)，且焦准距p的大小(p=2)”.

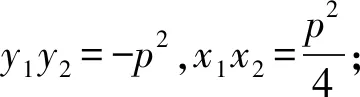
4)“△AFG,△CQG的面积为S1,S2”表征：△AFG,△CQG的面积要借助两个三角形的位置特征，采用个别顶点的坐标表示该三角形的面积,会给解题带来方便.

明确设问指向与目标：

1)“p的值及抛物线的标准方程”表征：“p”与“抛物线的标准方程”具有等同性，即知道p的值，就能够写出y2=2px，反之亦然.

总之，第1)小题主要考查抛物线的标准方程、几何性质，属于送分小题，更是增强学生解题信心的“兴奋剂”；第2)小题通过面积比来考查直线与抛物线的位置关系，虽属基础知识，但主要考查运算求解能力和综合应用能力，难度较大.该题平凡中藏有能力考查，对考生的数学素养要求较高，是一道值得探究的好题.

3 解法探究

3.1 第1)小题

抛物线的标准方程结构简单，参数只有一个焦准距p,不论怎样命制试题，只要抓住题目条件“焦点F(1,0)”，回归教材，就可以直接写出该抛物线的标准方程y2=4x.

3.2 第2)小题

思路1根据题目表征解读可知，从过焦点F的直线AB的方程设置方式入手，顺着三角形的重心G位置，确定坐标关系(根与系数的关系)与面积比的关系作为解题的逻辑起点，有下面的解法：

解法1避免对直线AB位置关系的分类讨论，可设过焦点F(1，0)的直线AB的方程为x=ky+1，与抛物线方程y2=4x联立得y2-4ky-4=0.因为点A,B是过点F的直线与抛物线的交点，设A(x1,y1),B(x2,y2)，则y1y2=-4.设Q(xQ,0),则直线AC的方程可设为x=my+xQ,与抛物线方程y2=4x联立得y2-4my-4xQ=0，设抛物线上的点C(x3,y3),易得y1y3=-4xQ.

设重心G(xG,0),根据三角形的重心定理的坐标关系，得

y1+y2+y3=0,x1+x2+x3=3xG，

解得

y3=-(y1+y2).

因为点A，B，C在抛物线y2=4x上，则

所以

又y1y3=-4xQ，且y3=-(y1+y2)，解得

由于△AGQ与△CGQ共底边GQ，根据三角形的面积公式可得

即

因为△AFG与△AGQ有共同的高|y1|，根据三角形的面积公式可得

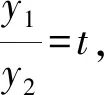
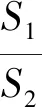
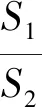
且

y1y2=-4，

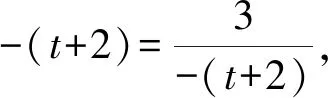
解法2对直线AB的位置关系进行分类讨论.当直线AB⊥x轴时，焦点F恰好是AB的中点，重心G不会在x轴上，不符合题意，故直线AB的斜率一定存在.不妨设为k(其中k>0)，则直线AB的方程可设为

y=k(x-1)(其中k>0)，

与抛物线方程y2=4x联立，化简可得

k2x2-(2k2+4)x+k2=0.

设A(x1,y1),B(x2,y2),根据韦达定理可得

则

设点C的坐标为C(x3,y3)，由重心坐标公式可得

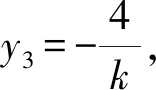
则

即

由斜率公式可得

从而直线AC的方程为

令y=0，可得

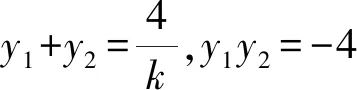
则

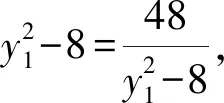
则点G的坐标为(2,0).

注思路1是从过焦点F的直线AB的方程设置入手，需要思考该直线与x轴的位置关系(垂直与否)；另外，该解法中用到以下结论：

结论1过点(m，0)(其中m>0)的直线与抛物线y2=2px(其中p>0)相交于点A(x1,y1)，B(x2,y2)，则y1y2=-2pm(其中m>0,p>0).

解法3设A(t2,2t)，B(xB,yB),C(xC,yC),重心G(xG,yG)，则直线AB的方程为

代入y2=4x，得

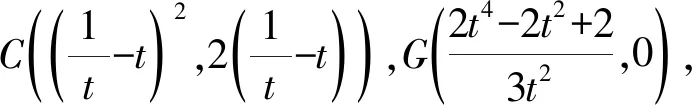
y-2t=2t(x-t2),

得Q(t2-1,0).

由点Q在焦点F的右侧，知t2>2，从而

令m=t2-2，则m>0，从而

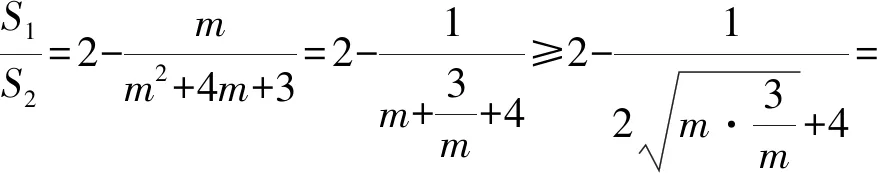
解法4设A(t2,2t)，B(xB,yB),C(xC,yC),重心G(xG,0).由于AB是抛物线的焦点弦，借助焦点弦端点坐标关系式

可得

t2xB=1， 2tyB=-4，

解得Q(t2-1,0).余下同上(略).

注本解法没有用联立方程组、消元和韦达定理，而是用了焦点弦端点坐标关系式，解题过程更简单.

4 问题拓展与推广

解得h=-pab.设点Q(q,0)(其中q>xG>h>0)，同理可得

q=-pac.

由三角形的重心定理，可知

且

从而

c=-(a+b)，

于是

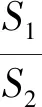
若点A在第一象限内的抛物线上时，则点B在第四象限内的抛物线上，此时令

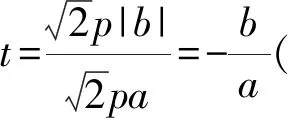
则

由于1-t2=(2-t)(2+t)-3，于是

故重心G(2h,0).

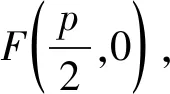
5 教学启示

本题以直线、抛物线和三角形的重心等知识点作为材料背景，将面积比的最值问题作为研究方向，属于平凡常见的题型.通过命题专家的巧妙安排和精心“打扮”，该解析几何问题作为2019年浙江省数学高考压轴题，凸显了命题人既要贯彻新课标的考查方向、又要考查考生的数学核心素养水准的命题意图，真是一道“常规题蕴涵能力深度，平凡法彰显素养水准”的好题.学生解此题虽然视角广，入手容易，但要获取满分真不容易.

因此，在数学学习时，教师一定要强化数学概念的理解，重视数学思想方法的培养和数学运算能力的提升，课堂教与学中一定要有意做一些数学题的研究，并尝试将其进行推广，才能够有效提升学生的数学核心素养，不能靠“刷题”来提高解题能力.