A unified optimal planner for autonomous parking vehicle

Dequan ZENG, Zhuoping YU, Lu XIONG, Peizhi ZHANG, Zhiqiang FU

School of Automotive Studies,Tongji University,Shanghai 201804,China;

Clean Energy Automotive Engineering Center,Tongji University,Shanghai 201804,China

Abstract In order to reduce the controlling difficulty caused by trajectory meandering and improve the adaptability to parking into regular lots, a versatile optimal planner (OP) is proposed. Taking advantage of the low speed specificity of parking vehicle, the OP algorithm was modeled the planning problem as a convex optimization problem. Collision-free constraints were formalized into the shortest distance between convex sets by describing obstacles and autonomous vehicle as affine set. Since employing Lagrange dual function and combining KKT conditions,the collision-free constraints translated into convex functions.Taking the national standard into account, 5 kinds of regular parking scenario, which contain 0°, 30°, 45°, 60° and 90° parking lots, were designed to verify the OP algorithm.The results illustrate that it is benefit from the continuous and smooth trajectory generated by the OP method to track, keep vehicle’s stability and improve ride comfort, compared with A* and hybrid A* algorithms.Moreover,the OP method has strong generality since it can ensure the success rate no less than 82%when parking planning is carried out at the start node of 369 different locations.Both of evaluation criteria,as the pear error and RMSE in x direction,y axis and Euclidean distance d,and heading deviation θ,are stable and feasible in real tests,which illustrates that the OP planner can satisfy the requirements of regular parking scenarios.

Keywords: Optimal trajectory,autonomous parking vehicle,regular parking lots,generality,convex optimization

1 Introduction

With the rapidly increasing ownership of car and occupy of land resources [1], parking lots is scarcer and parking space smaller, it is great challenge for a driver,both physically and psychologically. In consequence,the adverse effects are not only sharply erasing of convenience and comfort by driving,but also frequently rising of parking accidents,such as scratches,collisions or traffic jams. Therefore, automatic/self-parking vehicles are the future development trend. As one of its key technologies,planning method becomes a research hotspot in universities and enterprises worldwide[2-4].

The early and mature work for parking trajectory planning is the one using a geometric approach [5], which is based on a combination of straights, arcs, clothoids,etc.In[6],single circular trajectory method,which can be divided into three parts,that is,a straight,a circular arc and another straight respectively,is employed to implement parallel and vertical parking.To take the initial position of car into account,double circulars’trajectory is developed for vertical parking in [7]. However, since the trajectory curvature is discontinuity in connection of two parts, the tire is worn increasingly as having to shut down for steer [8-10]. For solving the problem, a robust grey-box control method is proposed to modify double circular strategy for parallel parking[11].As the same, double-constant-velocity trajectory is generated by introducing the concept of “transition radius” and“tangency radius” [12]. In contract, another prevalent implementation is adopted curve with continuous curvature function [13-15]. Liang [16] and Kawabata [17]employ Bezier curve to smooth the trajectory which is generated on multiple arcs. Similarly, A parametric Bezier curve directly has been designed to generated path for parallel and vertical parking[18,19].However,these methods are specially designed for parking specific scenarios and sensitive to the initial parking pose,which are lack of generality.

To unify path planner for parking,Zheng[20]presents a method based on rapidly-exploring random tree(RRT)with non-holonomic constraint and kinematic model of vehicle.For optimizing the search efficiency,target preference and bi-RRT are used [20]. In [21], the distance metric couples both heading angle and Euclidean distance for taking the constraint of the maximum steering angle into account.Literature[22]integrates modelbased target trees into RRT, which speeds up the algorithm. However, the core of RRT is to use a random seed expanding nodes, which leads to a large randomness of the generated path,and it is difficult to guarantee the planning efficiency and track quality[23,24].Other than the random sampling method of RRT,graph search can guarantee the consistency [25] and optimality of trajectory [26]. A state-based planner with a different control-set is developed,which is integrated on a priori map information derived from the blueprints of a parking lot,for automated valet parking[27].In[28],hybrid A* is implemented for real parking, which plots a continuous vehicle state to discrete configuration in the grid map.This modification guarantees the execution of path,but sacrifices the completeness [29]. In order to improve the planning efficiency, Chen [30] introduces an extended version of space exploration guided heuristic search(SEHS)method,which considers the orientation of a vehicle in the space exploration phase to achieve knowledge about driving directions. However, the grid resolution and composed of the connected grids are always difficult problem for graph search method [31].Therefore, lots of machine learning method have been presented,like support vector machine(SVM)[32],artificial neural networks(ANN)[33],radial basis functions networks (RBFN) [34], and General Radial Basis Function (GRBF) [35]. Nevertheless, lots of new challenges are inevitable in the application of machine learning for parking,like optimality,block box,massive samples,etc.

In order to generate optimal trajectory with continuous curvature for keeping the adaptability to park into regular lots,a unified optimal planner(OP)is proposed.Considering the low speed specificity of parking vehicle, the OP algorithm models the planning problem as a convex optimization problem, which employs the internal point method to solve the problem. In order to verify the universality of OP, 5 kinds of regular parking scenario, which contains 0°, 30°, 45°, 60°and 90°parking lots, were designed according to the national standard[36].The rest of paper is structured as follows:problem definition in Section 2,unified optimal planner in Section 3,experiments and discussions in Section 4,and conclusion and future work in Section 5.

2 Problem definition

In general, the trajectory planning problem is a twopoint-boundary-value problem with a objective function,given two fixed points(starting point and end point)and lots of constraints (upper and lower limits of variables),as shown in equation(1)[37].

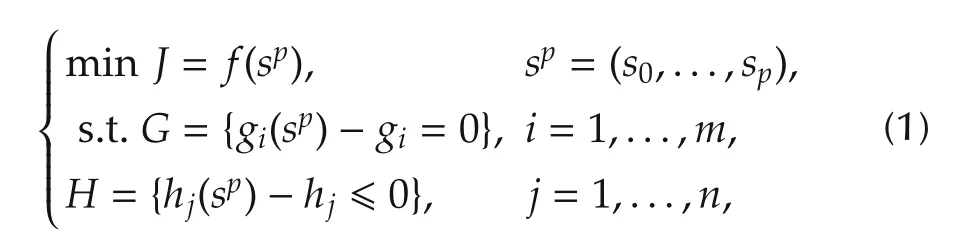
where J is objective function,sp=(s0,··· ,sp)is planned sequence of trajectory nodes, p is the total number of nodes, G is set of equality constraints, H is set of inequality constraints, m and n are the total number of constraints respectively.

3 Unified optimal planner

Since that the local optimal solution is the global optimal solution, it is benefit to concretize and transform the parking planning problem into a convex optimization problem for solving to obtain the global optimal trajectory. Through the formal description of the constraints and objectives for each part of parking planning and appropriate deformation, the problem is presented in the unified form of convex optimization in below.Moreover,a strategy of accelerating solution is introduced.

3.1 Equality constraints

The start node sstartand target node stargetconsist of the initial value constraint for planner, as that the start mostly selects the vehicle’s current pose,and the target is the parking pose in the target lot. The initial value constraint gst(s0,sp)is defined as follow,

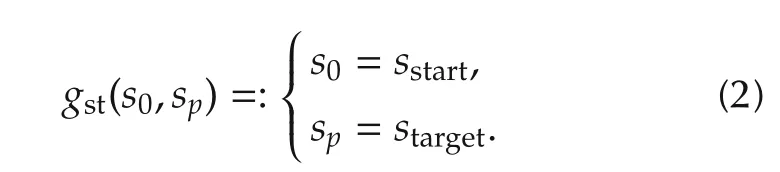
For low-speed scenarios such as autonomous parking,there is no phenomenon of heavy slip-angle,sideslip or roll that should be taken vehicle’s handling stability into account. Therefore, the kinematic model is sufficient to describe the movement of vehicle’s pose s(x,y,θ,v)under the input u of acceleration a and steer angle δ. The vehicle posture point s(x,y,θ,v) is selected in the center of the rear axis with the coordinate point is z(x,y). Key vehicle parameters contain axle base L, vehicle width 2l1, distance l2from rear axle to tail and distance l3from rear axle to head. Under the sampling rate Δt in time k with u(ak,δk)as control input,the vehicle will move from the current position sk(xk,yk,θk,vk)to sk+1(xk+1,yk+1,θk+1,vk+1),according to the kinematic model constraints gmodel(sk+1):

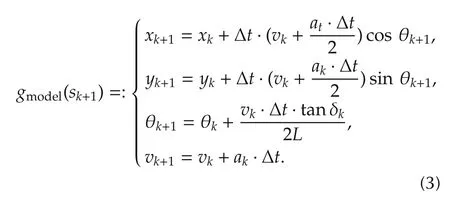
3.2 Inequality constraints

The planning is carried out in the environmental map provided by the perception system.When the areas outside the map,the safety cannot be judged,so the vehicle must ensure that every point on the vehicle body is in the map. Environment boundary constraint hmap(zk) is defined as

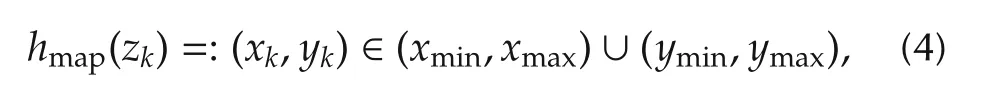
where(xmin,xmax)is the vertical boundaries of the map,and(ymin,ymax)is the horizontal boundaries of the map.

Restricted by the physical structure of vehicle actuator,the velocity v and control quantity u of autonomous parking trajectory should be within a reasonable range.Define the executor constraint hactor(vk,uk)as

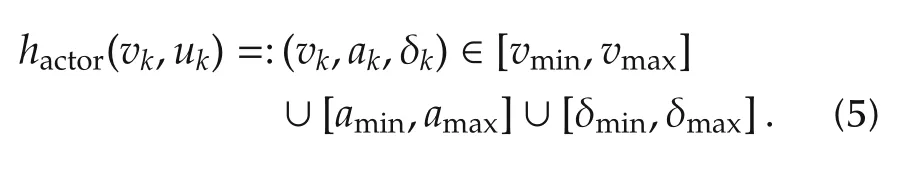
Collision-free constraint requires that the distance between any point zegoon the parking vehicle’s body and any point zobswithin the obstacles in the environment is greater than the minimum safe distance dsafe.That is,

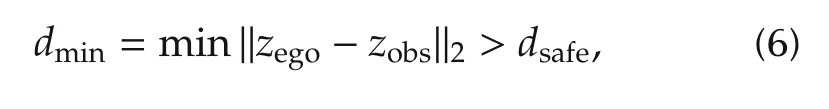
where‖·‖2is 2-norm,which is the Euclidean distance.

To formalize the description of obstacles, it is an assumption that all obstacles in the environment are convex polygons (for concave polygons, it could be converted into convex polygons by expansion and fill).Then,any point zobsof obstacles Oobswith convex polygons satisfies the following conditions:

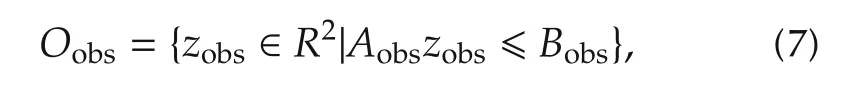
where Aobsis the multinomial coefficient for obstacles’polygons,and Bobsis the polynomial value.

Similarly,the parking vehicle is convex polygon,

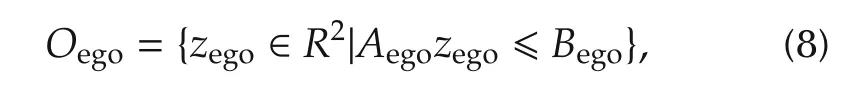
where Aegois multinomial coefficient for parking vehicle polygons,Begois polynomial value.

Therefore, the collision-free constraint described in equation(6)could be specifically expressed as

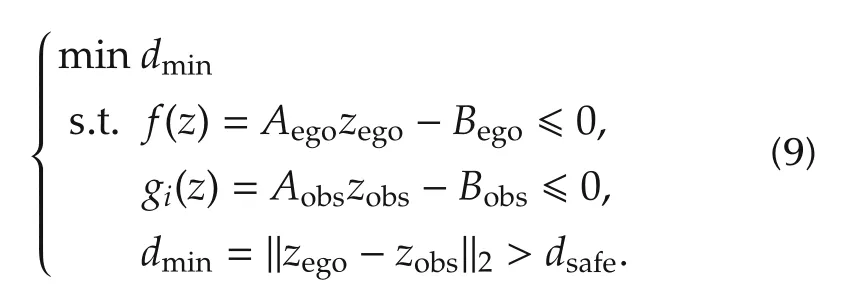
Since both autonomous parking vehicle and obstacles are convex sets described by affine sets, the dual problem of equation(9)is[37,38]

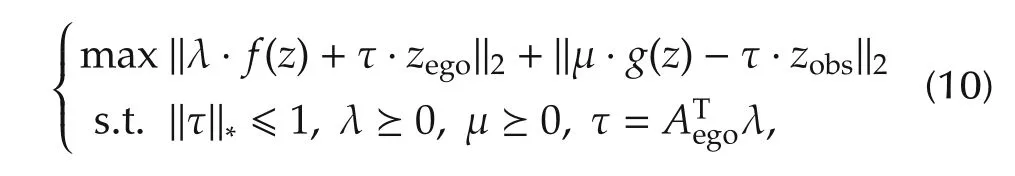
where λ and μ are Lagrangian variables.

Since equation(10)satisfies KKT conditions[37,38],meanwhile,parking vehicle and obstacles are described in affine sets,equation(9)can be converted into

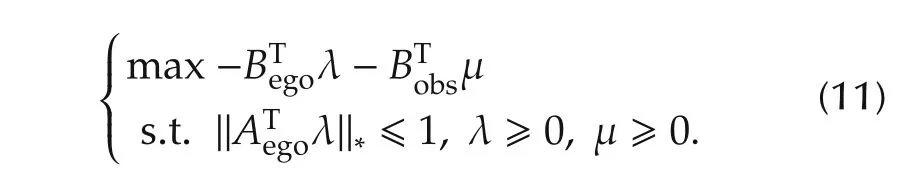
Finally,the collision avoidance constraint hsafe(zego,zobs)described in equation(6)is

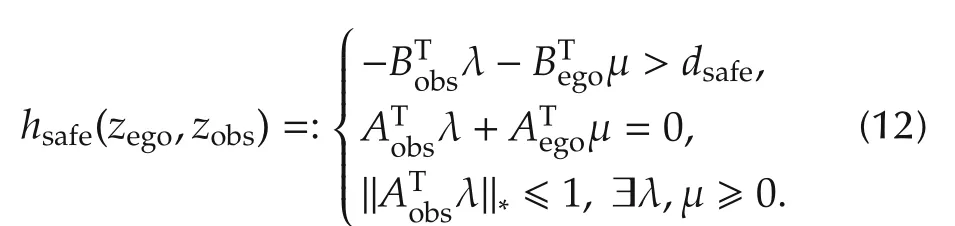
3.3 Objective function

The trajectory of autonomous parking planning should not only consider the economy(shortest path or shortest time),but also consider the comfort requirements of passengers when executing the trajectory(for low-speed parking conditions,comfort is reflected in less changes in speed and direction). Therefore, optimization objective function J is defined as

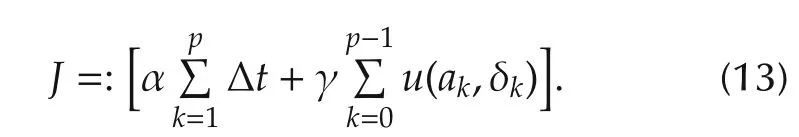
3.4 Convex problem

In combination with equations(2)-(5),(12)and(13),the specific form of the planning problem described in equation(1)can be obtained as shown in equation(14),which means the autonomous parking planning problem is a convex optimization problem, and it can be solved by using the interior point method.

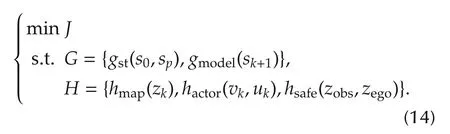
3.5 Solution strategy

The variables to be solved in parking trajectory planning problem(14)are:vehicle pose s(x,y,θ,v),control quantity u(a,δ), Lagrange variable λ and μ. As the generated trajectory with p nodes, and the map with M obstacles within polygon variable N, the total number of variables to be determined is (p+1)(6+N(M+1)).For a complete parking(starting from the effective storage location identified by perception and ending at the target storage location),the trajectory’s length is no less than 10m, and there are 50 discrete nodes with 0.2 m distance interval.There are 1122 variables to be solved in the simple scenario where the obstacles are only two obstacle lots location on the left and right and one lane boundary.In more general scenarios,the variables to be solved multiply. To speed up computing, the collision avoidance constraint hsafe(zego,zobs)in equation(12)can be converted into equation(15),and the initial value obtained as the collision-free constraint hsafe(zego,zobs)can be substituted into equation(14)for solving.

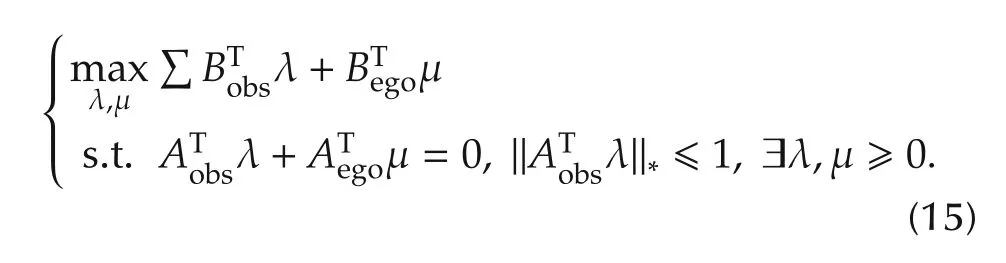
4 Experiments and discussions

Based on Ubuntu16.04LTS environment, the processor is Intel Core i5-4200H@2.80GHz,memory 8.00GB,DDR4,2133Hz,and the solver of the algorithm adopts IPOPT.The platform is an E50 electric vehicle modified by the laboratory(as shown in Fig.1),and the parameters are shown in Table 1.

Fig.1 E50 Parking platform.

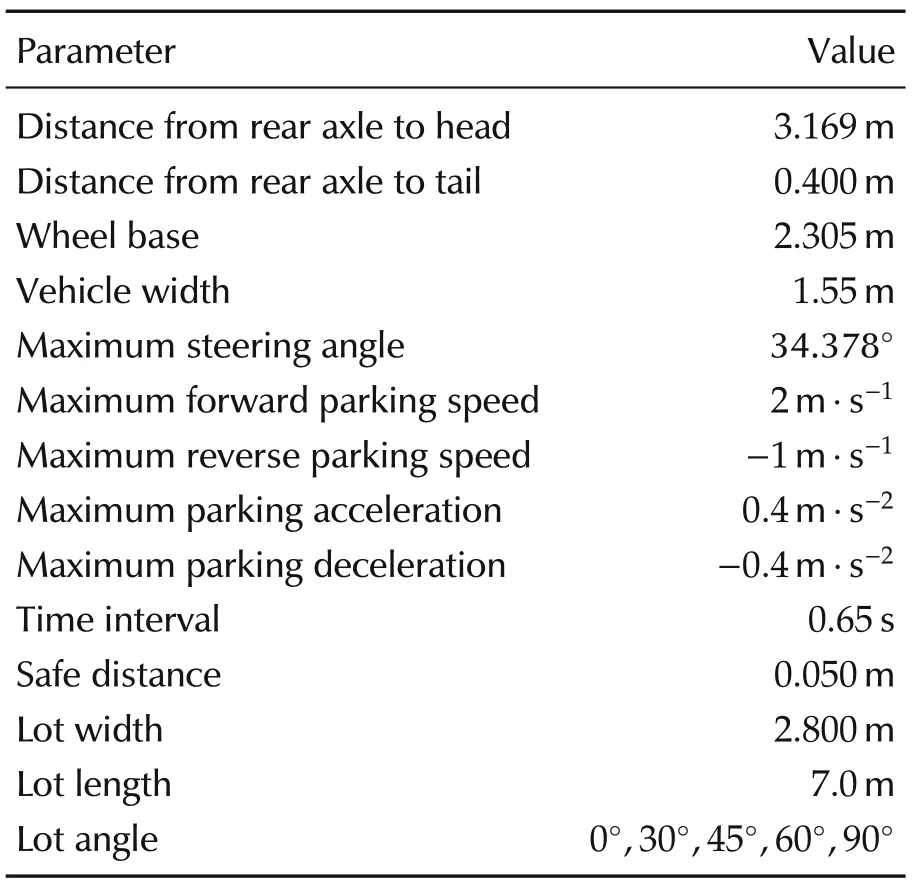
Table 1 Key parameters for tests.

4.1 Trajectory tests

According to the national standard[36],5 kinds of regular parking scenario, which contains 0°, 30°, 45°, 60°and 90°parking lots, were designed. The HA* (hybrid A*) algorithm [28], which is based on RS curve extension,is compared with the universal octa-neighborhood search A*algorithm[27].

Fig.2 shows the planned trajectories by the three algorithms for the 0°lot(parallel parking)scenario.Fig.2(a)shows that all the algorithms can generate collisionfree paths connecting the start node and the target node. However, the heading planned by OP method is smoother than the results of A* and hybrid A* algorithms, as shown in Fig.3(b). The heading jump of A* algorithm is the most severe, since the direction changing unit is 45°when node extends with octoneighborhood method.Unlike A*,since that the hybrid A* algorithm employs the vehicle’s minimum turning radius constraint and the extension process is mostly in the form of straight segments plus arcs, the heading change is stable, but not continuous. The results illustrate that the trajectory planned by OP algorithm not only is smooth and continuous to track,but also satisfy the requirements of vehicle stability and ride comfort.

Figs.3-6 show the results for 30°lot, 45°lot, 60°lot and 90°lot (vertical parking) respectively. All the three algorithms can plan the collision-free trajectory. However, the trajectory and heading generated by the OP method could remain smooth and continuous, which indicates that the OP algorithm in this paper could meet the parking requirements under regular conditions and has certain generality.

Fig.2 Planning for 0° lot(parallel parking).(a)Trajectory.(b)Heading.

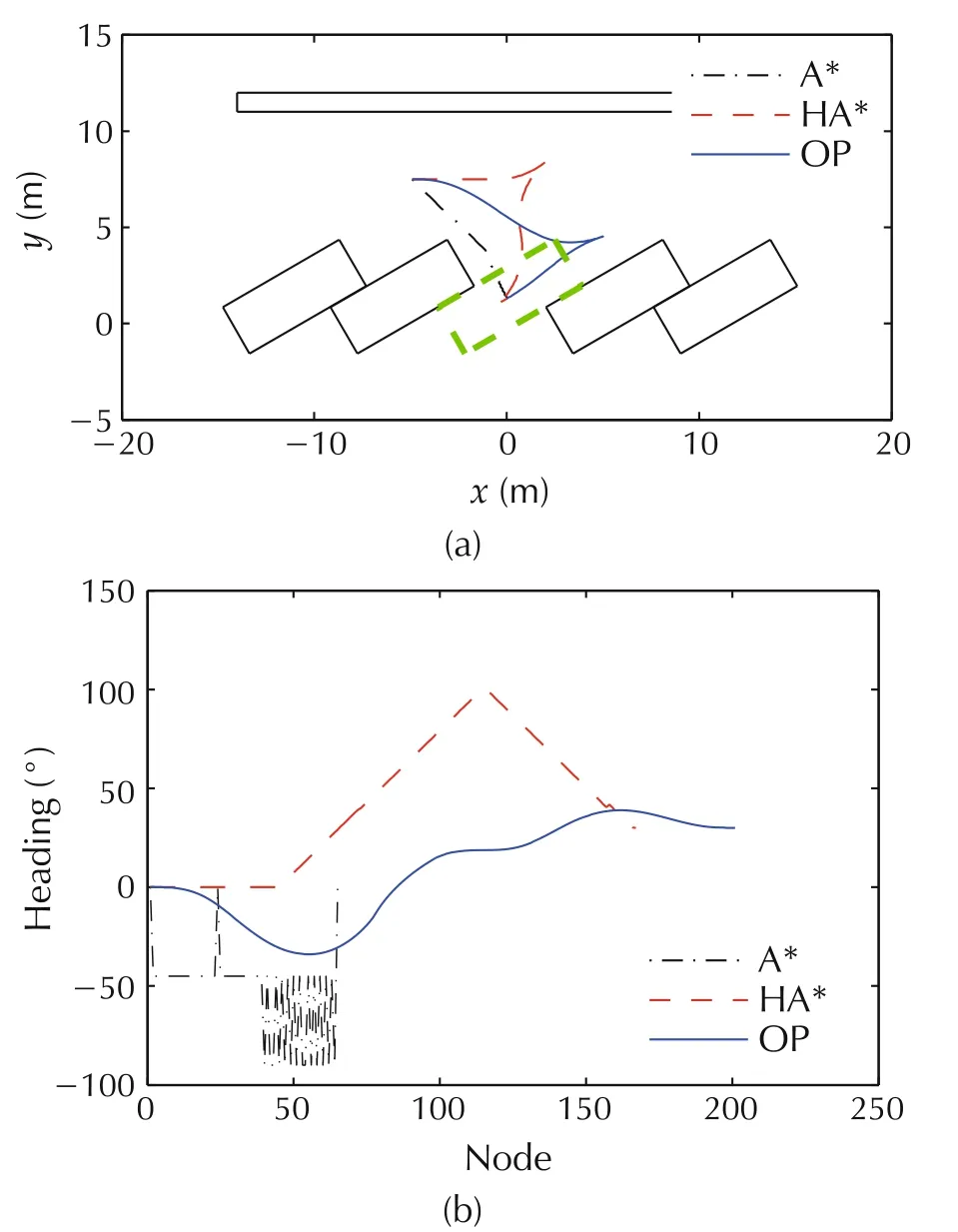
Fig.3 Planning for 30° lot.(a)Trajectory.(b)Heading.

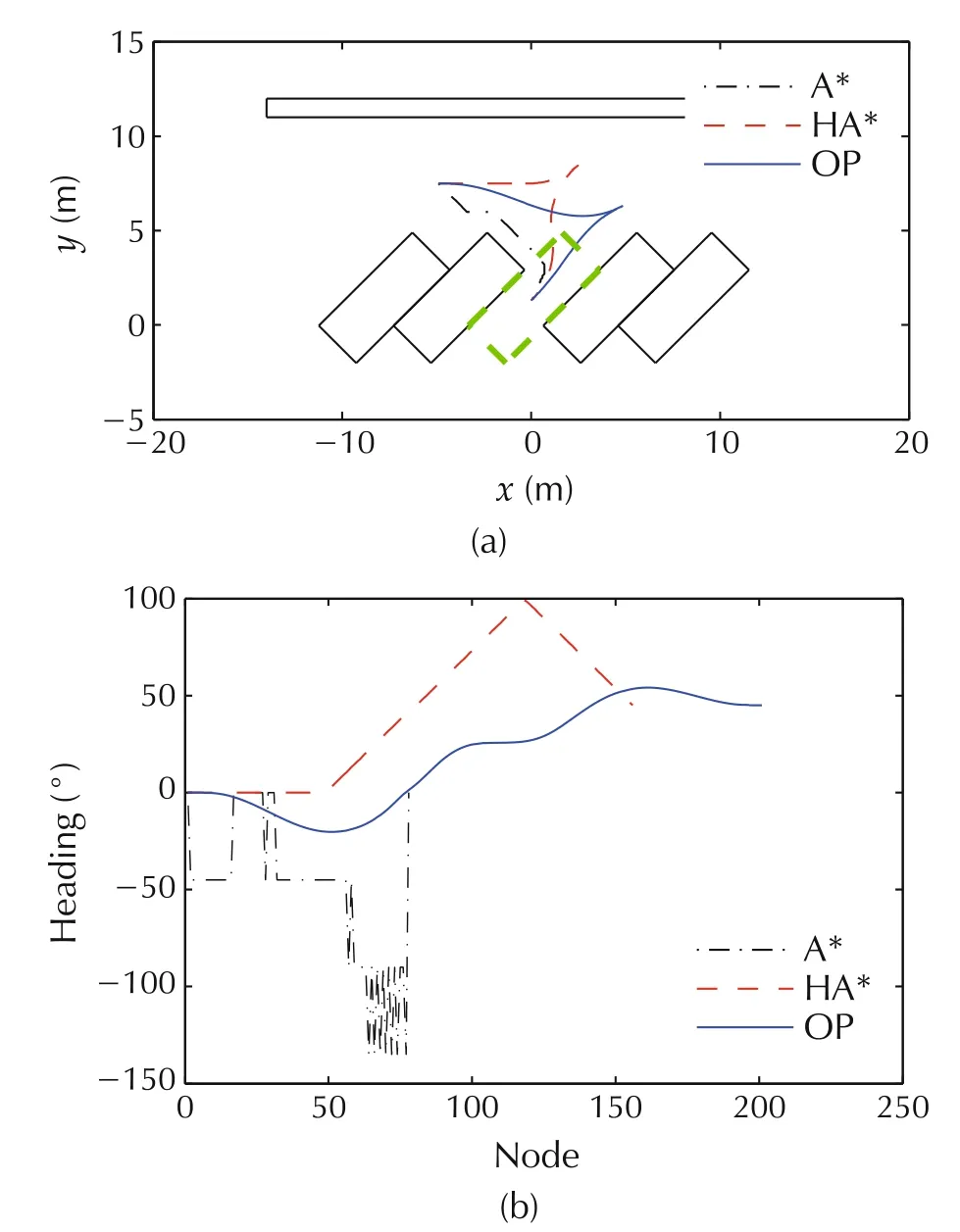
Fig.4 Planning for 45° lot.(a)Trajectory.(b)Heading.

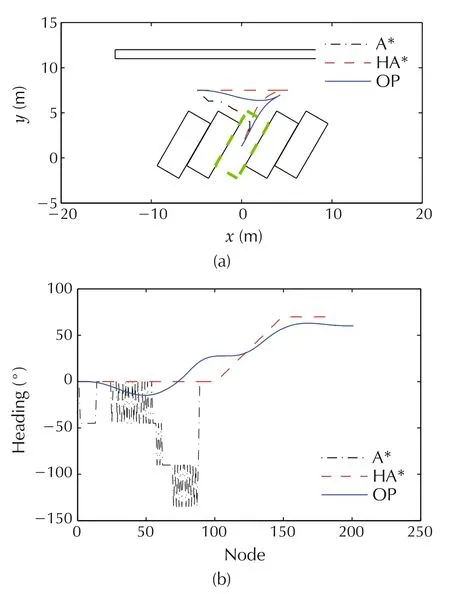
Fig.5 Planning for 60° lot.(a)Trajectory.(b)Heading.

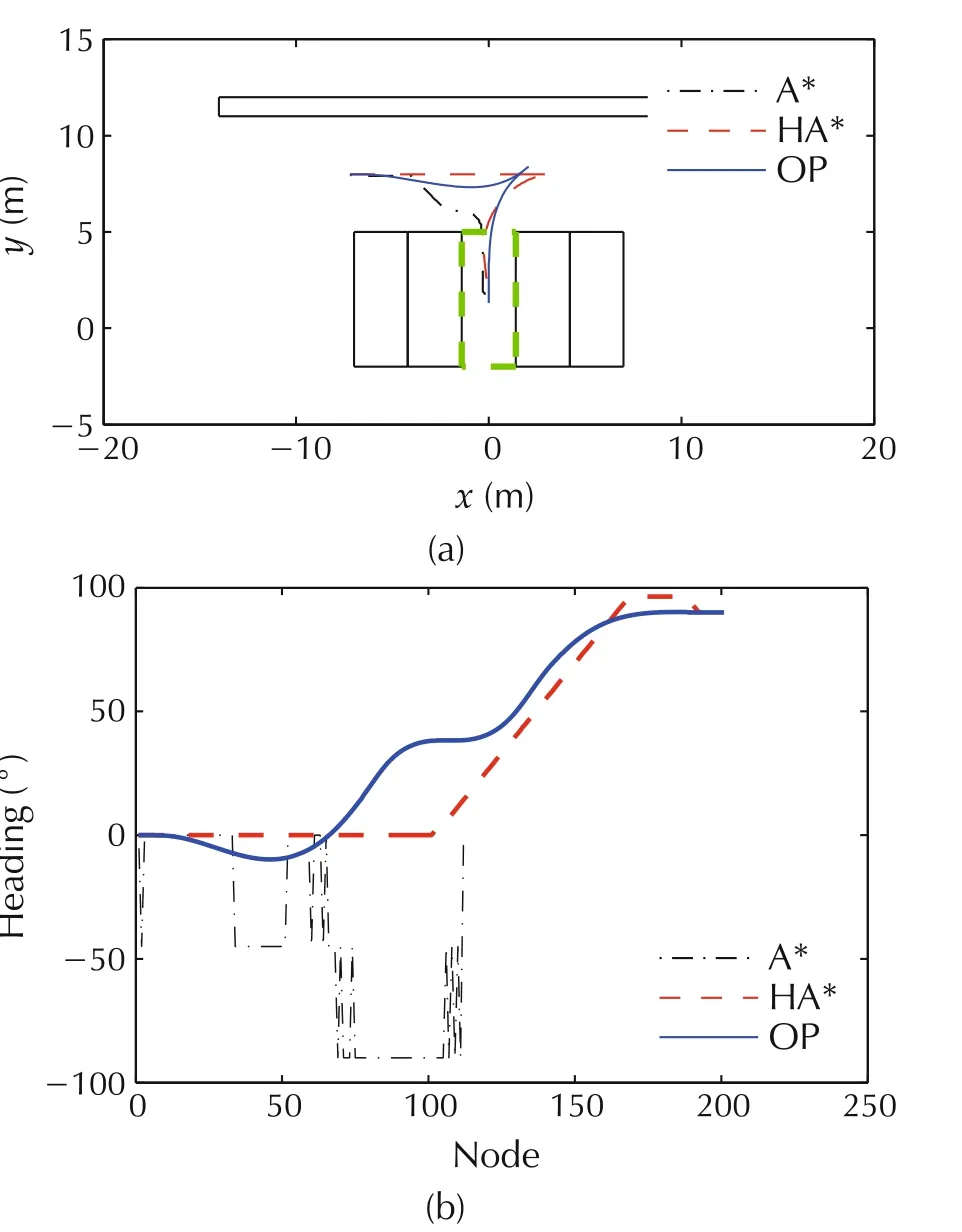
Fig.6 Planning for 90° lot(vertical parking).(a)Trajectory.(b)Heading.

4.2 Generality tests

To further verify the generality of the OP algorithm proposed in this paper, the start parking pose ranges from(-10 m,6 m)to(10m,10m)with 0.5m a step according to the scenarios in Figs.2-6.Then,there are 369 different start nodes in total as shown in Fig.7. Moreover,as listed in Table 2,it is the success rate tested for the three algorithms with 5 scenarios under 369 different start nodes.

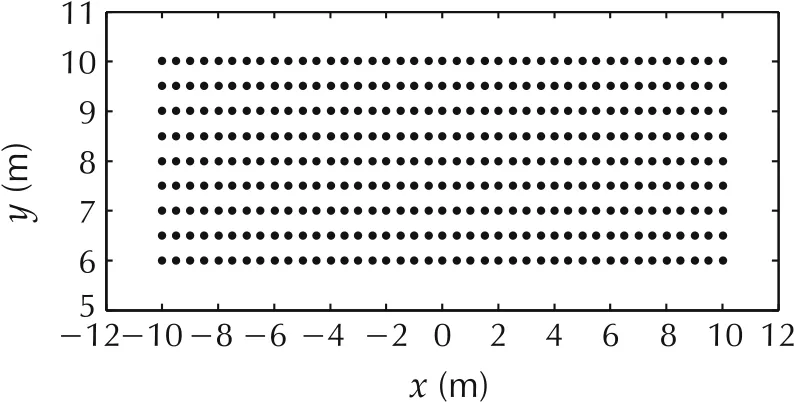
Fig.7 Start node for parking.

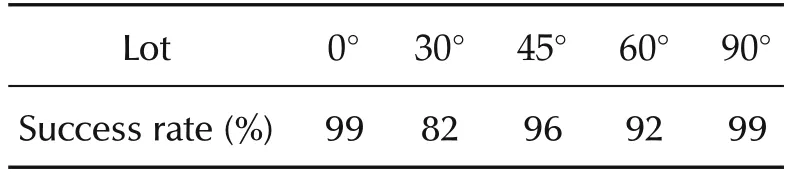
Table 2 Success rate for the three algorithms.

The success rate of OP algorithm is more than 92%,except that in the 30°lot scenario is as low as 82%.The data illustrate that the generality of OP method could be competent to regular parking mission.

4.3 Real tests

The parking system, as shown in Fig.8, for real tests is developed based on E50 platform, shown in Fig.1,where a bird’s eye view preceptor [7] is projected to identify valid lots, a hierarchical motion controller[39,40] is employed to make the deviation of parking vehicle converge to zero respecting to a given reference trajectory,and an dead reckon(DR)with extended Kalman filter(EKF)is designed as locator[41,42],which could compute the spatial position and heading angle of the vehicle in real time.The real parking lot’s configurations are listed in Table 3.

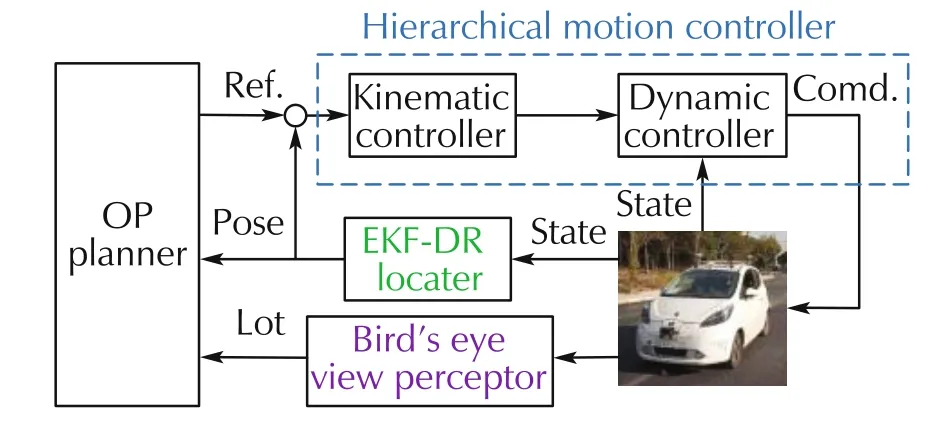
Fig.8 Parking system.

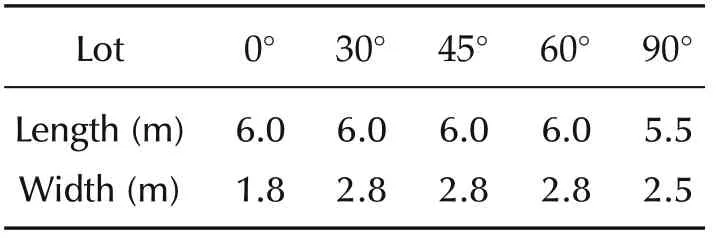
Table 3 Real parking lot’s configurations.

As shown in Figs.9-13, ten repeated experiments were carried out for each lot.In order to quantify the actual effect of parking planner,the pear error,root mean squared error(RMSE)and its’mean error are employed into distance deviation,such as in x direction,y axis and Euclidean distance d,and heading deviation θ.As listed in Table 4,when parallel parking(0°lot),the peak error in x direction is less than 0.1 m,while the peak error in y axis is less than 0.1 m when the lot is 30°. In other lots, the peak error in both x direction and y axis is no less than 0.1 m,but no more than 0.2 m.The peak error of Euclidean reaches d maximum value with 0.16 m at 45°lot, which may be related to the large peak errors in both the x and y directions, but the value is always within 0.2 m.However,the heading error θ of the peak value appears at 0°lot,which is 2.91°.The mean value of the peak error indicates that the distance peak error (x,y,d) of the parking system could be kept within 0.2 m and the direction peak error θ within 3°. The indexes from RMSE listed in Table 5 are more aggressive since reducing the error level to less than 0.1 m in the distance(x,y,d)and less than 2°in the direction θ Both of the indexes illustrate that the designed parking system is stable and feasible,which also proves that the OP planner can satisfy the requirements of regular parking scenarios.

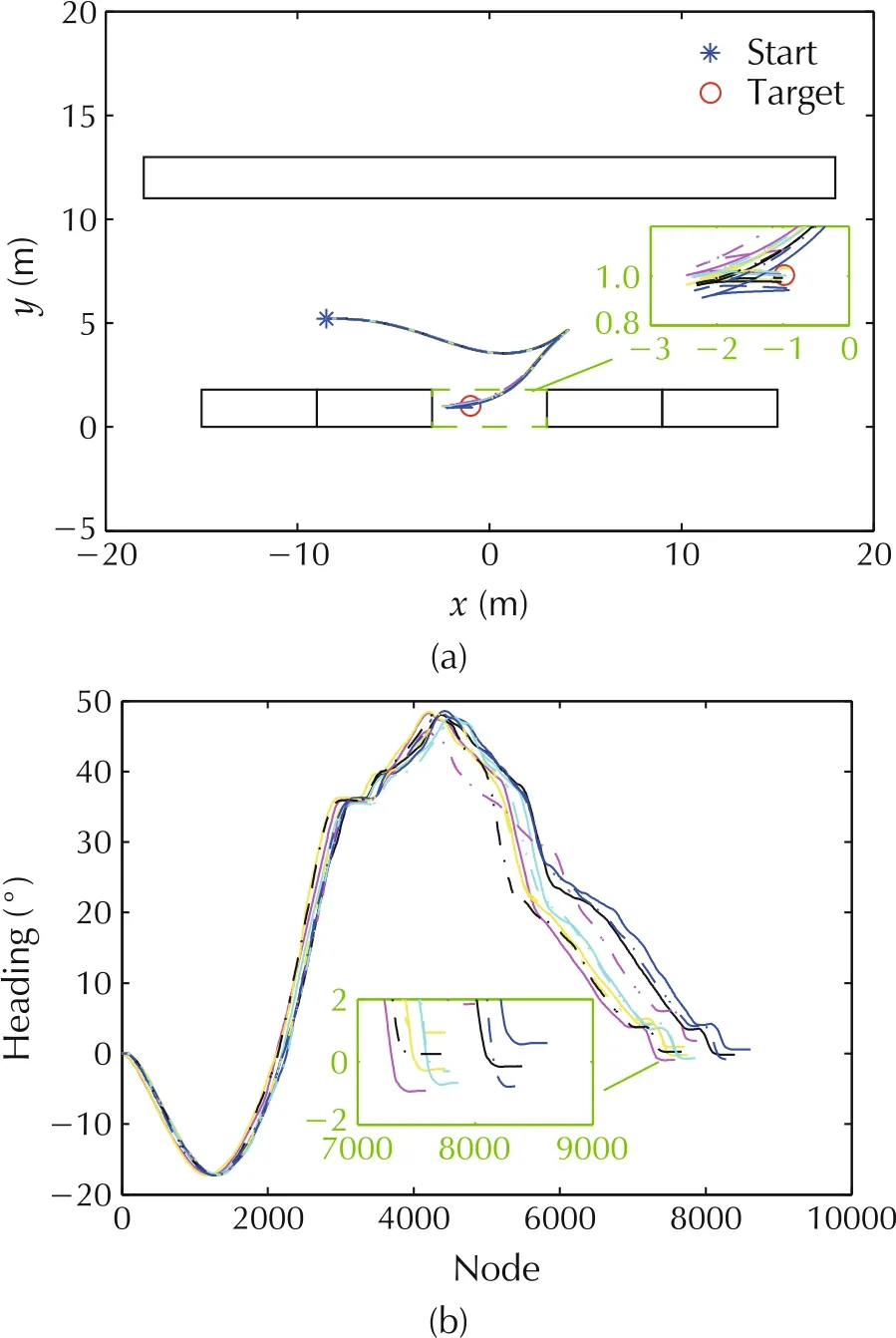
Fig.9 Real trajectory for 0°lot(parallel parking).(a)Trajectory.(b)Heading.

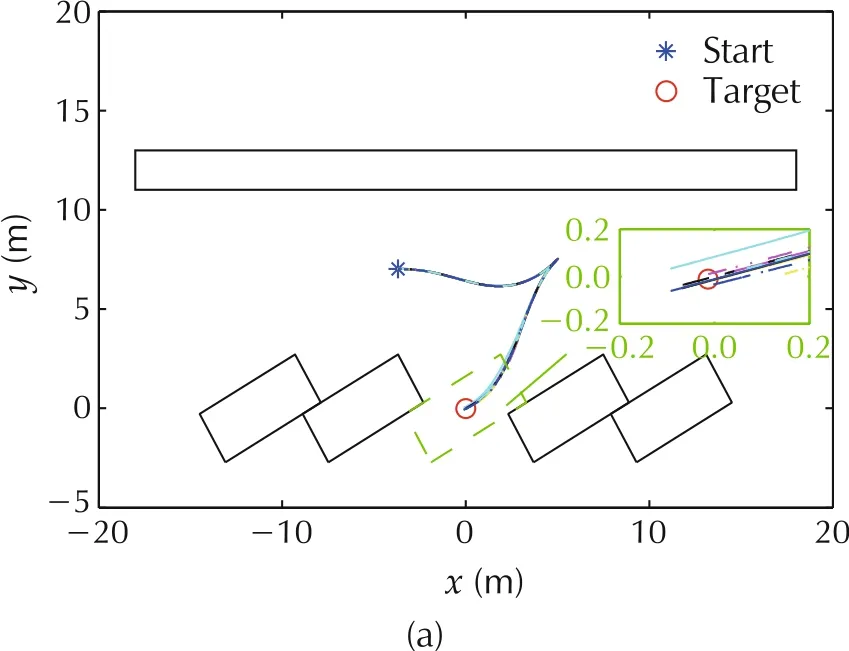
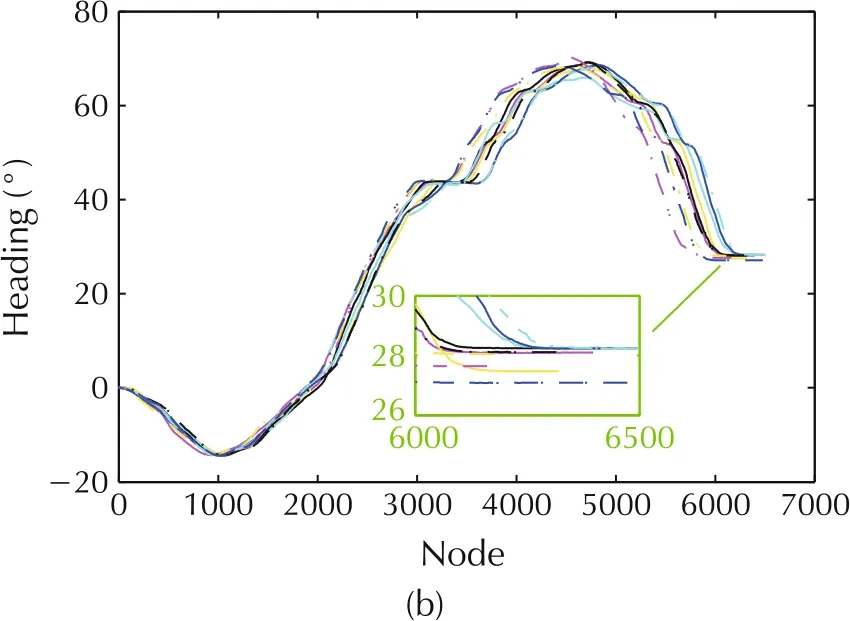
Fig.10 Real trajectory for 30° lot.(a)Trajectory.(b)Heading.

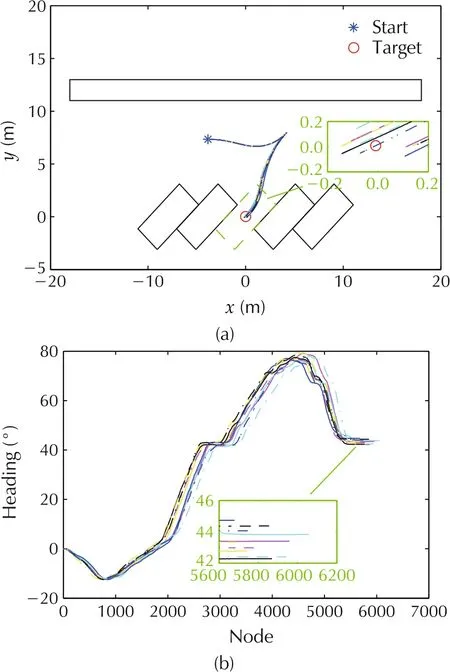
Fig.11 Real trajectory for 45° lot.(a)Trajectory.(b)Heading.

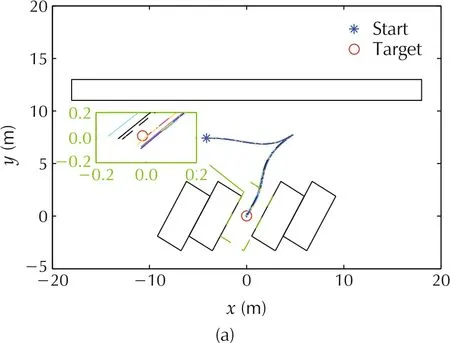
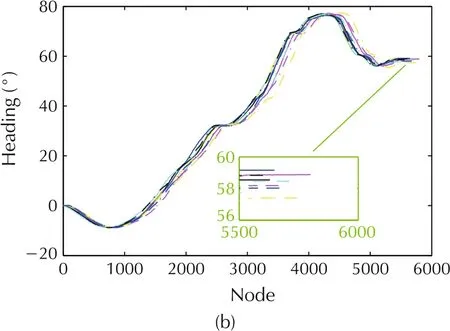
Fig.12 Real trajectory for 60° lot.(a)Trajectory.(b)Heading.

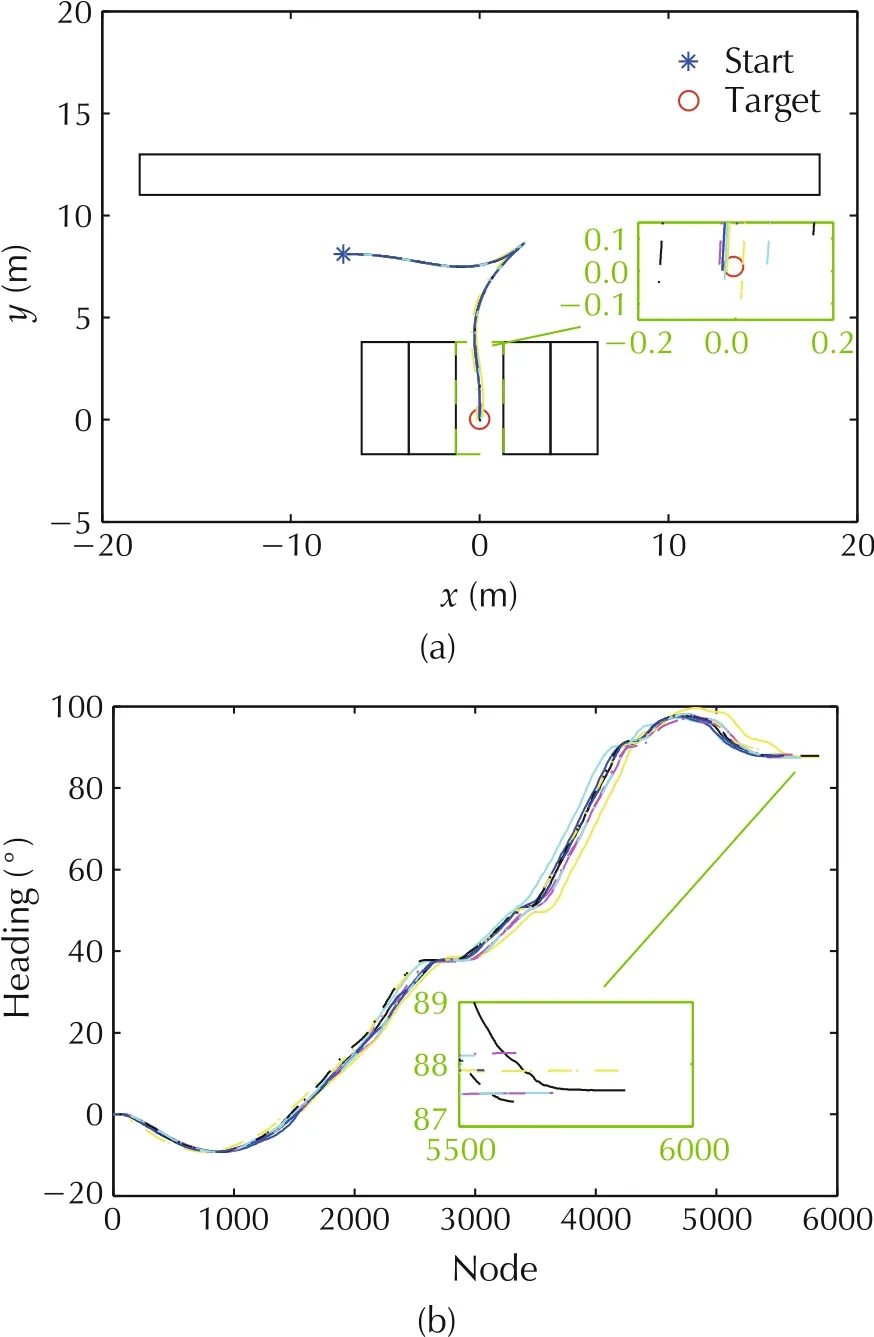
Fig.13 Real trajectory for 90° lot(vertical parking).(a)Trajectory.(b)Heading.

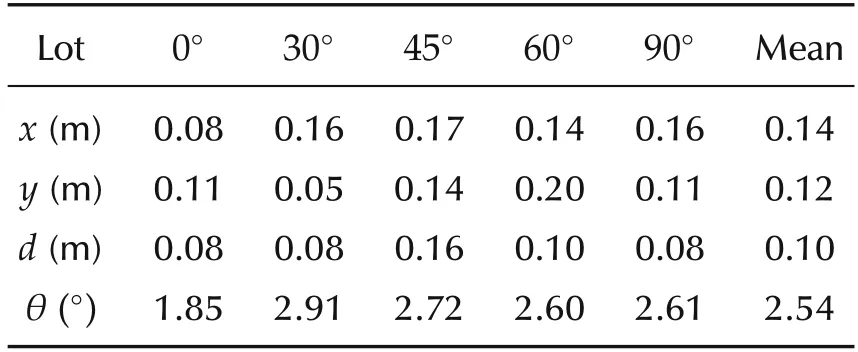
Table 4 Peak error.

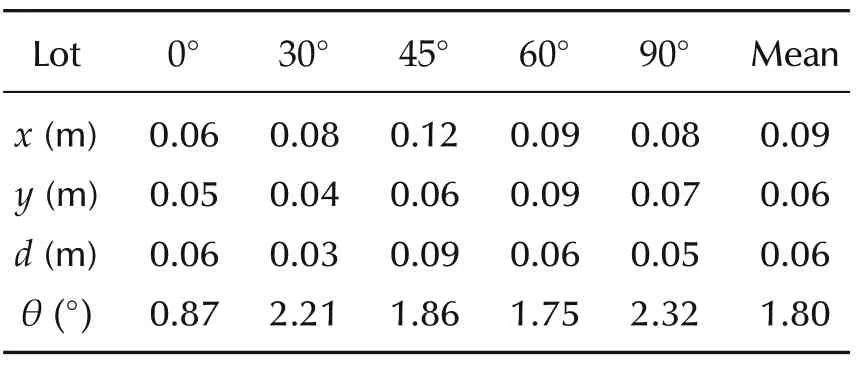
Table 5 RMSE.

5 Conclusion and future work

A unified optimal planner (OP) is presented to generate optimal trajectory with continuous curvature for keeping the adaptability to park into regular lots. The problem of autonomous parking trajectory planning is unified into a convex optimization problem,and the interior point method is used to solve the problem. The OP method could be competent to regular parking missions since that the generality of OP method is verified due to the success rate being no less than 82%, which tested in 5 kinds of regular parking scenario with 369 different start nodes. Both of evaluation criteria, as the pear error and RMSE,illustrate that the OP planner can satisfy the requirements of regular parking scenarios.

The future work will focus on improvement on the algorithm success rate. Efforts to study the real-time performance of the algorithm and speed it up will be fruitful.

Acknowledgements

The authors thank the assistance from other people of the School of Automotive Studies,Tongji University.