Two-stage on-board optimization of merging velocity planning with energy management for HEVs

Bo ZHANG, Wenjing CAO, Tielong SHEN

Department of Engineering and Applied Sciences,Faculty of Science and Technology,Sophia University,Tokyo,102-8554,Japan

Abstract This paper proposes a two-stage hierarchy control system with model predictive control(MPC)for connected parallel HEVs with available traffic information. In the first stage, a coordination of on-ramp merging problem using MPC is presented to optimize the merging point and trajectory for cooperative merging. After formulating the merging problem into a nonlinear optimization problem, a continuous/GMRES method is used to generate the real-time vehicle acceleration for two considered HEVs running on main road and merging road, respectively. The real-time acceleration action is used to calculate the torque demand for the dynamic system of the second stage.In the second stage,an energy management strategy(EMS)for powertrain control that optimizes the torque-split and gear ratio simultaneously is composed to improve fuel efficiency. The formulated nonlinear optimization problem is solved by sequential quadratic programming(SQP)method under the same receding horizon.The simulation results demonstrate that the vehicles can merge cooperatively and smoothly with a reasonable torque distribution and gear shift schedule.

Keywords: Merging,model predictive control(MPC),powertrain control,parallel hybrid electric vehicles(HEVs)

1 Introduction

Traffic jams, exhaust pollution and energy crisis are becoming increasingly severe with the development of transportation system [1]. Reference [2] presented that as a kind of non-renewable resource, two thirds of the oil used around the world currently goes to power vehicles. There have been plenty of researches focused on the efficiency of the internal combustion engine(ICE)in the last several decades[3-5].However,traffic environment also affects the driver’s action of a vehicle,which leads to the performance of the fuel consumption.Some traffic scenarios such as the merging, overtaking, etc.are inevitable in the transportation system. Therefore,the fuel economy can be improved by improving the management maneuvers in the specific scenarios.

On-ramp merging is a common condition and the inappropriate merging maybe cause traffic jams and traffic accidents.The traffic jams caused by rough merging maneuver leads to energy waste. Therefore, a reasonable merging maneuver contributes to improving fuel economy.The early researches focused on the macroscopic traffic model with ramps scenario.Hegyi et al.[6]developed the macroscopic traffic flow model METANET, in oreder to find the optimal merging velocity with model predictive control (MPC) controller with the on-ramps and off-ramps condition considered. In the paper [7],a platform based on freeway merging capacity simulation program(FMCSP)is built to investigate the performance of merging strategies in congested traffic case.Papageorgiou et al.[8]developed a traditional feedback controller for real-time merging and this controller was applied within a toll plaza. Weng et al. [9] used the classification and regression tree method to model the merging behavior at the available zones to minimize the time-to-collision.The results showed that the proposed strategy can generate a safe merging path in work zones.Reference [10] developed a game theoretical model to describe the cooperative motion, the merging problem aimed to determine the give-way behavior in the merging section.All the papers mentioned above are considered from the view of macro-models.Hidas[11]developed a new lane change model to model the merging and weaving in the intersection using intelligent agent concepts. The proposed strategy is tested under several real-life situations in the ARTEMiS traffic simulator.Cao et al. [12,13] focused on the coordination control for cooperative safe and smooth merging in the on-ramp condition to reduce traffic jams and drivers’mental load.However, energy consumption was not considered directly in these papers.

On the other hand, hybrid electric vehicles (HEVs)as a kind of new energy automobile has caught public attention because of its high efficiency and fuel economy [14]. Energy management strategy (EMS) of HEVs aiming at deciding the power-split method between the engine and motor depending on driver’s demand has been a significant way to improve fuel economy.References [15,16] reviewed and classified the main proposed EMS for different categories of HEVs. For the purpose of practical application,the strategies with the ability to determine the action in real time drew much interest.Rule-based EMS has been widely implemented in production because of its low cost and small computational load [17]. For instance, fuzzy logic-based controller is popularly used as an early rule-based method in different driving conditions [18]. Subsequently, the optimization-based energy management control strategies are developed to improve the optimal performance in recent decade.Many optimal control theories are proposed and applied on EMS. An energy management controller based on game theory is designed to minimize the fuel consumption and NOxemissions with the equilibrium between the driver’s demand and the powertrain efficiency considered.The results show that the proposed controller provides better fuel economy comparing with the baseline, a so-called BOPOM controller[19].Besides,MPC is an effective scheme to deal with the real-time issue with a receding horizon optimization.Zhang et al.[20-22]proposed and developed the energy management method for plug-in HEVs with MPC strategy, and the formulated nonlinear optimization problem is solved using contimuation/generalized minimum residual (C/GMRES) method. Moreover, the traffic information is widely used for improving safety and efficiency in the transportation system[23].Particularly,the traffic information is popularly used for velocity prediction.An adaptive equivalent consumption minimization strategy(AECMS)taking the predicted driving conditions into account is proposed in the paper [24].The equivalent factor is adjusted in real time,in order to realize the energy minimization.In the paper[25],a bilevel MPC scheme is presented to optimize the torque split and gear shift schedule under the planning velocity trajectory.In the paper[26],a power-split strategy that combines a model-based velocity predictor for deciding the on-line operating mode with an efficiency based approach is proposed.In addition,Liu et al.[27]proposed a look-ahead energy management strategy for parallel HEVs based on fuzzy-based velocity prediction and reinforcement learning method, and the co-simulation is constructed to validate the performance of the proposed strategy in the hardware-in-the-loop platform.

It is considered that the combination of the merging trajectory optimization and power-split optimization for HEVs together will contribute to reducing traffic congestion and improving fuel economy.This paper proposes a two-stage hierarchy energy management system for the merging case with MPC strategy. In the first stage, an on-ramp merging problem is presented to optimize the merging point and trajectory, and a C/GMRES method is used to provide the control actions,i.e.,the accelerations of the two considered HEVs.In the second stage,the torque demand is determined by the real-time accelerations, and then an energy management problem for powertrain control to optimize the torque-split and gear ratio is formulated.This nonlinear optimization problem is solved by sequential quadratic programming (SQP)method during the same prediction horizon.

The rest of this paper is organized as follows.Section 2 will introduce the merging model and powertrain architecture for the considered parallel HEVs, and present the optimal control problem for the proposed hierarchy energy management system.Section 3 will present the simulation methods and discuss the results. Finally conclusions are drawn in Section 4.

2 System model

In this work,the ego vehicles are assumed to be two connected and automated vehicles(CAVs)with parallel hybrid powertrain.To simplify the system,only one car driving in the main lane and one in the merging lane respectively is considered.By using the vehicle to vehicle(V2V)information and the global position system(GPS)technology,the position information,speed information of the vehicles and the traffic state can be obtained realtimely.The overview of the two-stage hierarchy control system proposed in this paper is shown in Fig.1.

Fig.1 The real-time energy optimal control system with V2V and V2I.

Fig.1 shows that two automatic HEVs drive respectively on the main lane and merging lane.It is assumed that the position between the considered vehicles and the speeds of them can be obtained with the real-time communication technology.The considered vehicles on the main lane and merging lane are equipped with the identical parallel hybrid powertrain.The problem we focus on here is to generate cooperative merging actions and to optimize torque split with minimizing the energy consumption. In the first stage, the vehicles are considered as a particle, and an MPC scheme is proposed to optimize the acceleration sequences for cooperative merging with the safety and smoothness considered.The obtained accelerations are used to calculate the torque demand and then provided to the powertrain optimal controller in the second stage. In the second stage,a nonlinear optimization problem that decide the torque split and gear ratio is formulated to minimize the energy consumption. Since the acceleration sequences obtained in the first stage are used as the reference input of the controller in the second stage, to utilize the merging information adequately, the predicted horizon of the second stage should be less than or equal to the horizon of the first stage. Moreover, to reduce the calculation amount, the predicted horizon of the optimal controllers in the two stages is set to be the same.

In the following sections,we will firstly introduce the merging model and the optimal trajectory generation method with MPC,then the powertrain architecture for parallel HEVs and the formulated optimization problem will be presented.

2.1 Merging problem

The first stage of the proposed hierarchy system is the on-ramp merging problem, which is aimed to find the optimal acceleration to realize safe and smooth cooperative merging.As shown in Fig.2,the merging maneuver of one vehicle running on the main lane and one vehicle running on the merging lane is considered. Theses two vehicles are denoted as Vehicle 1 and Vehicle 2,respectively.

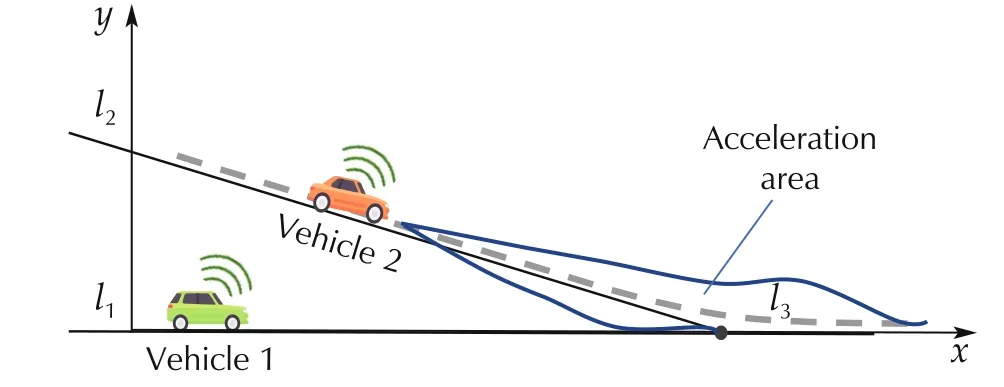
Fig.2 The model of the merging process.

2.1.1 The formulation for merging problem

Fig.2 shows that the two lanes are approximate to two straight lines,and the driving direction on the main lane is denoted as the positive direction of x-axis.The lane l1,l2represent the center line of the main lane and merging lane, respectively. l3, named “Cao-line”, is designed as a hyperbola connecting l1and l2[12].In accord with actual situation,as shown in Fig.2,there is an acceleration area where Vehicle 2 can adjust its speed and path for merging safety. Under the coordination defined above,the expressions of the lines are as follows:

where k and β represent the slope and the interception on the y-axis of l2,x and y denote the abscissa and the ordinate,α is a design parameter which determines the smoothness of l3.

Moreover, an extra variable b is introduced to draw the actual path of Vehicle 2.The y-axis position of Vehicle 2 can be expressed as follows:

where x2xdenotes the x-axis position of Vehicle 2, parameter b represents the deviation value away from the centerline of lane l3. We assume that Vehicle 1 drives on the centerline of the main lane l1.

The dynamic equation for the vehicles can be written as follows:

where

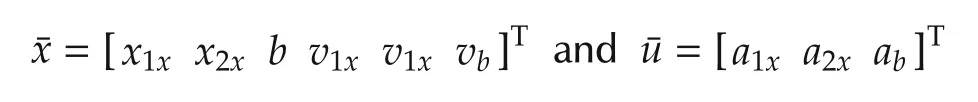
denote the state variable and control input.The physical significance of the variables are shown in Table 1.

Table 1 Meaning of variables.

2.1.2 The optimal merging trajectory generation with MPC

The MPC scheme is popular for real-time implementation. The policy of the optimization strategy can be described as follows: at the current time t, determine the real-time control actions we defined in the control problem,such that the cost function with respect to the control and state variables can be minimized along the predicted state trajectory during the predicted horizon T,and the control sequence can be obtained.Only the first control input is applied as the real-time control action.This process will be repeated with a sampling time Δt, i.e., at the next time instant t+Δt, the optimization will be repeated on the new sate. In this paper,an MPC-based merging trajectory is represented to optimize the merging trajactory and minimize the energy consumption.

The proposed two-stage hierarchy control system in this paper is under the same MPC frame, i.e., a uniform prediction horizon. In this section, the method to optimize the merging trajectory is presented. The control action ¯u is derived based on C/GMRES method in the first stage. The merging problem with MPC can be formulated as follows:

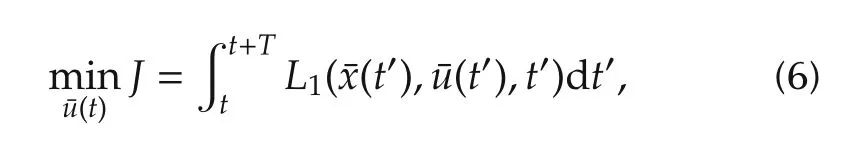
which subjects to the state function and the following constraints:

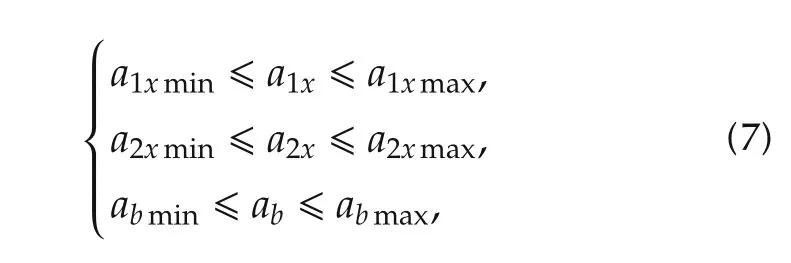
where T denotes the prediction horizon, a1xmin, a2xminand abmindenote the lower bounds of the acceleration.Similarly, a1xmax, a2xmaxand abmaxrepresent the upper bounds of the acceleration,respectively.The constraints ensure the vehicles satisfy under the physical conditions,such that the merging path is generated in the bound of available accelerations.

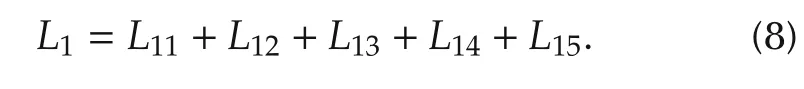
The first term L11represents the safety which is designed as follows:

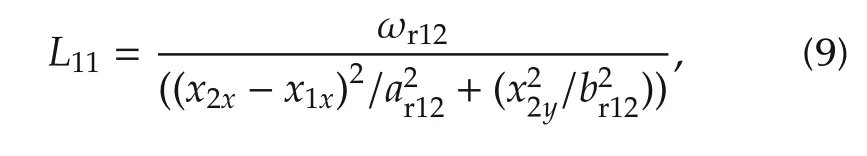
where ωr12is the weight, this term ensures the driving safety by forcing the relative distance between the considered vehicles longer than 0 m,thus the collision will never happen during the process.It should be noted that the term L11tends to the positive infinity as the horizontal distance between Vehicle 1 and Vehicle 2 tends to zero.Therefore,it is a kind of hard constraint that the vehicles must satisfy.This term avoids collisions between the two vehicles. The relative distance is reinforced by the constraint which is expressed as

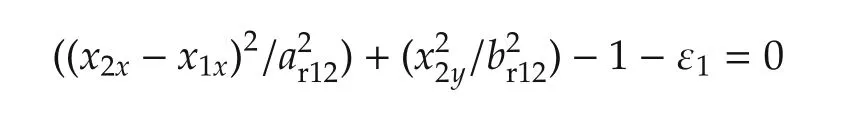
with the dummy variables ε1to improve the robustness,the constants ar12and br12should be designed reasonably for the safety and parallel running of the vehicles.

The second term L12can be written as follows:

where ωbis the weight,this term makes the merging vehicle always run as closely as possible to the centerlines of the fitting curve l3. Here two extra dummy variables ε2and ε3are introduced to improve the robustness with the relationship:

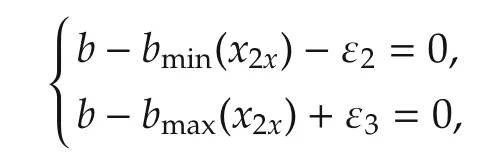
where bminand bmaxrepresent the motion interval of b,and they are expressed with respect to the x-axis distance of Vehicle 2.The details for the parameters can be found in reference[28].

The third term ensures that the vehicles achieve the desired velocity and drive within the road limit after merging.It is designed as follows:

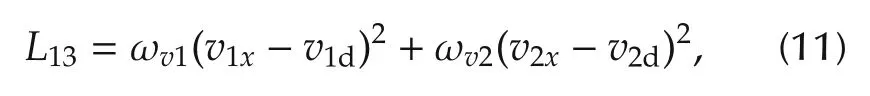
where ωv1and ωv2are the weights,and v1dand v2dare defined as the desired velocity given in advance.

The fourth term is designed as follows:

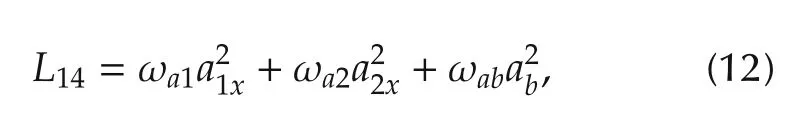
where ωa1, ωa2and ωabare also the weights. This term aims to minimize the accelerations to improve the passengers’ comfort and prevent the occurrence of severe acceleration.

The fifth term is related to the dummy variables εj(j=1,2,3),which can be designed as

where ωεj(j=1,2,3)are the weights,μj(j=1,2,3)are three designed parameters.The details about each term of the cost can be found in paper[28].

Then the formulated MPC problem is solved using C/GMRES algorithm, and the control sequence ¯u(t) is obtained by iteratively calculation. The acceleration sequence will be used as a reference input to the second stage. More details of the C/GMRES algorithm can be found in the reference[29].

2.2 Powertrain control problem

The focus of the second stage of the proposed system is on the optimal control for the hybrid powertrain.

2.2.1 The model for the hybrid powertrain

The two vehicles considered in this paper, i.e., Vehicle 1 and Vehicle 2 are assumed to be parallel HEVs.The powertrain architecture of Vehicle 1 is shown in Fig.3.The considered hybrid structure is comprised of an ICE,a motor, a battery, a gear box and a clutch. It can be noted that the cultch links the engine and motor. The vehicle dynamic model of the vehicles is expressed as follows:

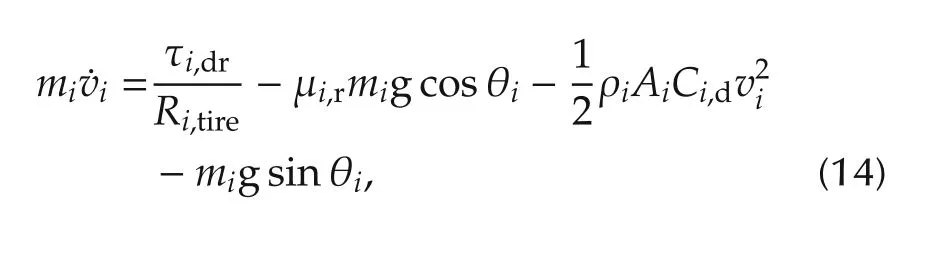
where i = 1,2 respectively represent the mark of Vehicle 1 and Vehicle 2.τi,drrepresent the torque demand,vithe velocity, and Ri,tirethe wheel radius. μi,r, g, and θi(rad) are the coefficient of the rolling resistance, the gravity acceleration,and the road slope,respectively.ρi,Ai,and Ci,ddenote the air density,the frontal area of the vehicle and the air drag coefficient,respectively.We can note that the real-time torque can be derived from the vehicle dynamic equation once the acceleration is given.It should be noted that Vehicle 1 drives on the centerline of the main lane.The velocity in the x-axis direction,i.e.,v1xis considered as the velocity of Vehicle 1,i.e.,v1.

Fig.3 The parallel powertrain architecture of Vehicle 1.

In addition, the engine speed ωi,erad/s and motor speed ωi,mrad/s, i=1,2 is decided based on the relationship of the velocity and the gear ratio, which is shown as

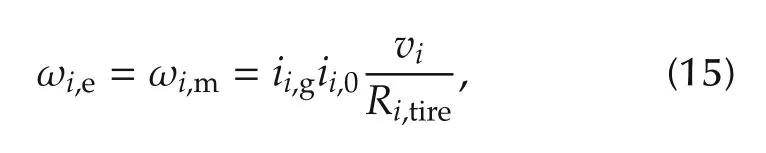
where ii,gand ii,0denote the gear ratio and the final differential gear ratio,respectively.

Based on the given torque demand,the toque split between the engine and motor should satisfy the following relationship:

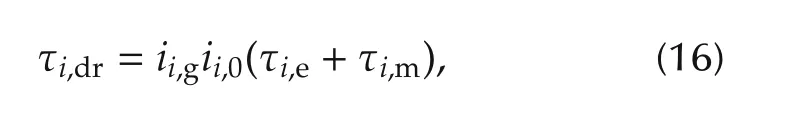
where τi,e(Nm) and τi,m(Nm) represent the engine torque and the motor torque,respectively.

For the hybrid powertrain,the dynamics of the battery is also a significant part to be considered.The battery dynamic affects the motor works,and the uniform dynamic is simply modeled in terms of SoC as the following expression.

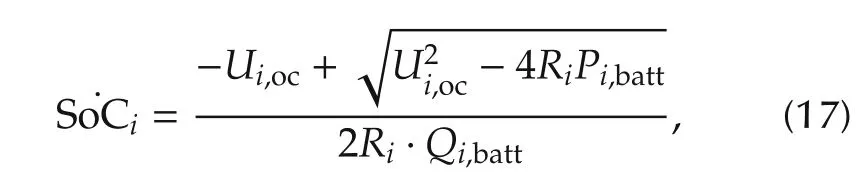
where Ui,oc(V)and Ri(Ω)are the open circle voltage and the internal resistance of the battery,both of which are functions with respect to SoCi. Qi,batt(Ah) is the maximum battery capacity. The battery power Pi,batt(W) is related with the motor torque and speed of Vehicle i,which is described as

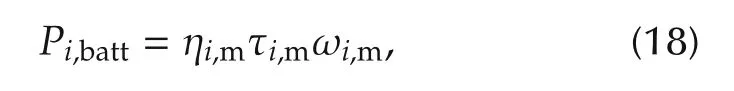
where ηi,mis the efficiency of the motor charging of Vehicle i, and it is modeled as a polynomial function in terms of motor speed and torque.

2.2.2 The optimization problem of powertrain management

With the acceleration sequence obtained by solving the merging problem over the same prediction horizon [t,t+ΔT], we aim to find the optimal control law ui=[ii,gKi]Tfor the powertrain to minimize the energy consumption.Here ii,gdenotes the gear ratio for Vehicle i,and Kithe torque distribution of it.The symbol i represents Vehicle i (i=1,2) in the following discussion.Therefore a nonlinear optimization problem is formulated as

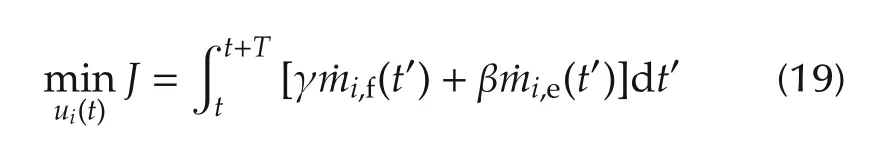
with the following constraints:

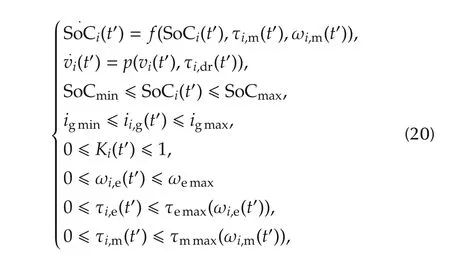
where ii,g(t′)and Ki(t′)should be satisfied the following relationship:

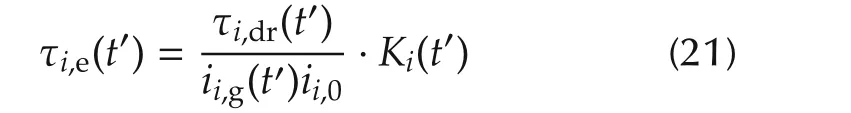
state variable xi= [vi(t′) SoCi(t′)]Trepresents the vehicle longitudinal velocity and SoC of the two vehicles,respectively, function f and p represent the dynamic equation(14)and(17), ˙mi,f(g/s)and ˙mi,e(kWh)denote the instantaneous fuel rate and power consumption in terms of the torque and speed,respectively.γ(¥/g)and β (¥/kWh) are the weighting coefficients which convert the amount of energy into the amount of money, the fuel rate ˙mfis a fitting polynomial equation in terms of engine torque and speed according to a Toyota fuel map, and the general form of the power consumption ˙mi,e(kWh)can be written as

where a4,a3υ,a2υ,.and a1υare constant parameters,andMoreover, in order to ensure the engine and motor work within the physical conditions, the speed follows the constraints:

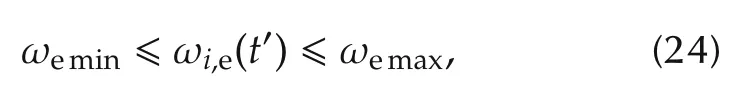
where ωeminand ωemaxdenote as the minimum and maximum speed of the engine.

The boundary torque of the engine and motor can be calculated by a fitting polynomial equation in regard to the real-time rotate speed, which can be presented as follows:

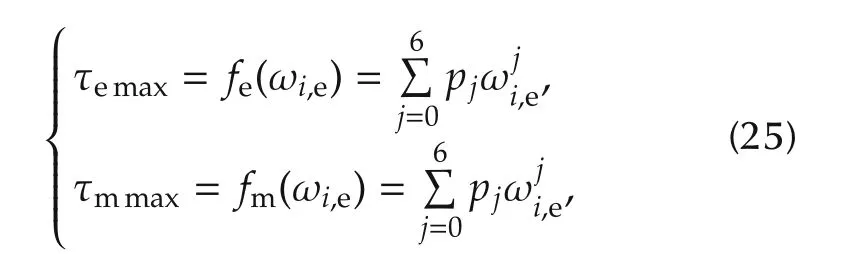
where pjand qj, j=0,...,6 are constant parameters.

In this subproblem, the prediction step N is determined by the sampling time Δt. After discreting the control inputs and state variables, a multiple shooting algorithm is proposed to decouple the dynamic equation constraints between the state xi(k)and xi(k+1)by introducing an extra artificial variable s = [s0··· sN]T,k=1,...,N-1.The details about the multiple shooting algorithm can be found in the references[30,31].Then the optimization problem over N steps can be summarized as the generalized form of nonlinear programming with constraints.

SQP method is used in this paper to solve the nonlinear optimization in this stage. The solution is generated by solving a quadratic programming(QP)subproblem. The SQP algorithm is implemented in MATLAB,and quadprog toolbox is used to generate the QP iterative solution. And the process repeats by renewing the iteration point.

So far, the whole optimal control actions can be achieved for this hierarchy control system.

3 Simulation results

Simulations are demonstrated in MATLAB/Simulink.A typical original condition is chosen.We will show the merging process firstly,and reveal the results of torque split and gear shift schedule for the powertrain control.The parameters of the vehicles and the merging problem are provided in Table 2.Moreover the initial conditions of the considered vehicles were set as x1x=59 m,x2x= 59 m, b = 59 m, v1x= 20 m/s, v1x= 9.9 m/s,vb= 0 m/s. This is a typical case that Vehicle 2 will follow Vehicle 1 on the main lane. Considering that the merging process is transient and rapid, the prediction horizon is set as T = 3 s, and the sampling time is set as Δt=0.01 s.The prices of fuel and power are approximate to γ=151.05/721¥/g and β=25¥/kWh.

The obtained merging trajectory is drawn in Fig.4,where the relative position in real time is drawn based on the simulation result.To clearly show the merging trajectory,the position of the two vehicles at time tλ=2λ(s),λ = 1,2,...,8 is shown in the figure, where the black circle and green cross represent the Vehicle 2 and Vehicle 1,respectively.The two vehicles kept an appropriate distance during the merging process.This result reveals that the merging can be realized safely.Fig.5 shows the time history of the variables. We can see that the accelerations of the considered vehicles are always kept in an available interval, a1x,a2x≤amax= 3 m/s2. The acceleration of Vehicle 2 varied more intensely than Vehicle 1.Just as what we assumed that Vehicle 2 cruises following the main lane vehicle. The dummy variable b changes no more than 10 m in this case.This means that the merging one,i.e.,Vehicle 2 does not run drastically away from the centerline of the lane.

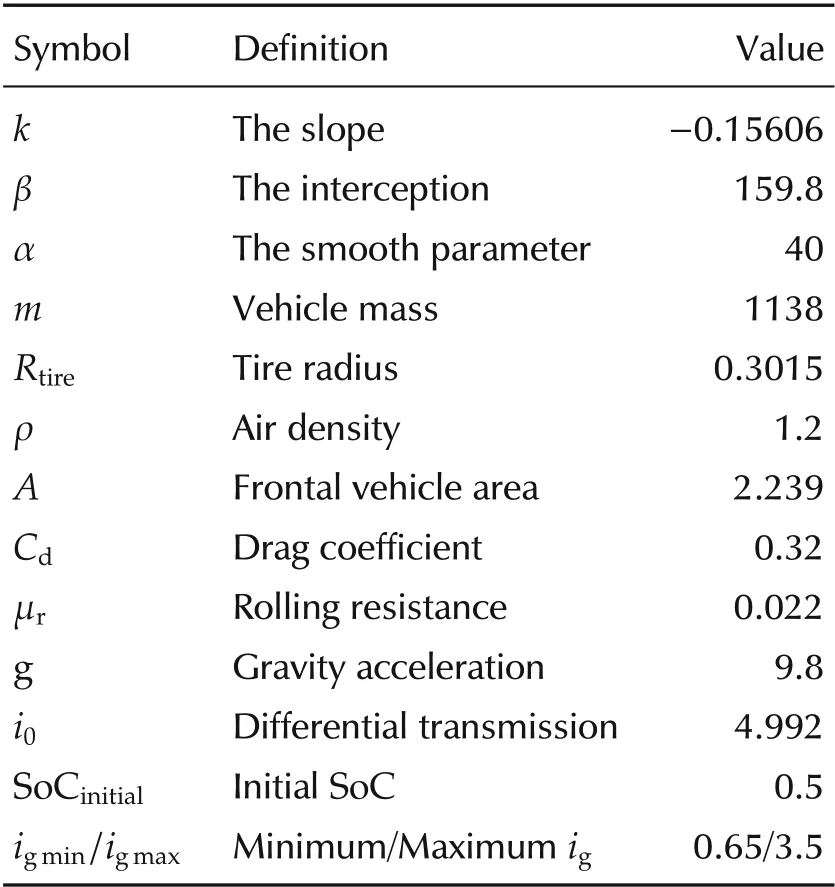
Table 2 Parameters of vehicle and merging.

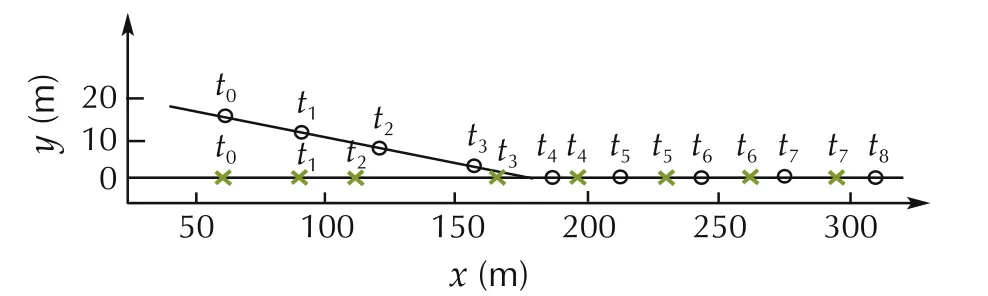
Fig.4 The merging trajectory.

Fig.5 The time history of the variables.

Fig.6 shows the torque split results. The engine of Vehicle 1 almost keeps inactive during the process, as Vehicle 1 keeps slow down to the desired velocity.The motor works to recycle the energy in this case. The motor can provide the total power during the steady driving in most of the time. Vehicle 2 keeps speed up with a sharp acceleration which leads to the torque split between the engine and motor which is a reasonable operation. The gear ratio results are shown in Fig.7. It should be noted that the gear shift schedule lies in a reasonable location. The speeds of the engine and motor are shown in Fig.8. In most of the time, the engine is not working and the motor can provide the power individually.It means that the engine assists the motor work in most cases.Fig.9 presents the fuel consumption and SoC state during the merging process.

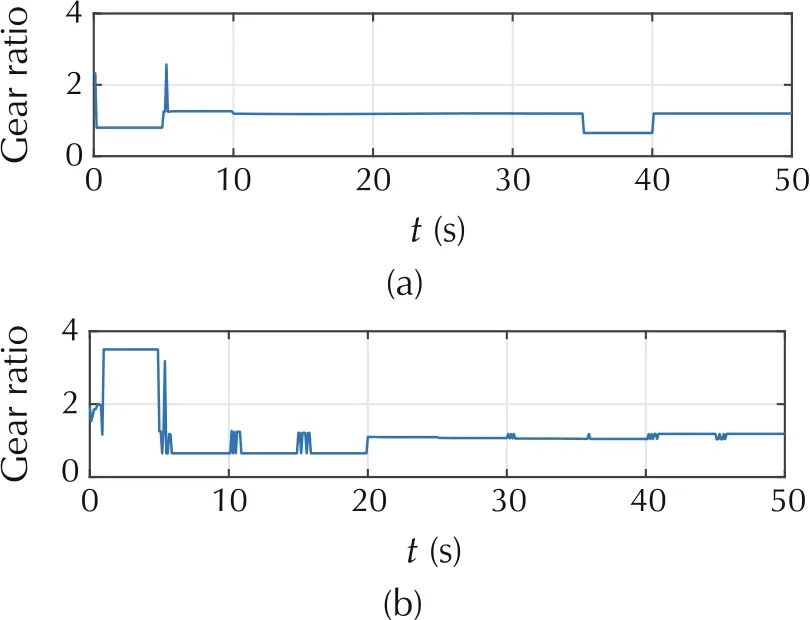
Fig.7 The gear ratio results for two vehicles.

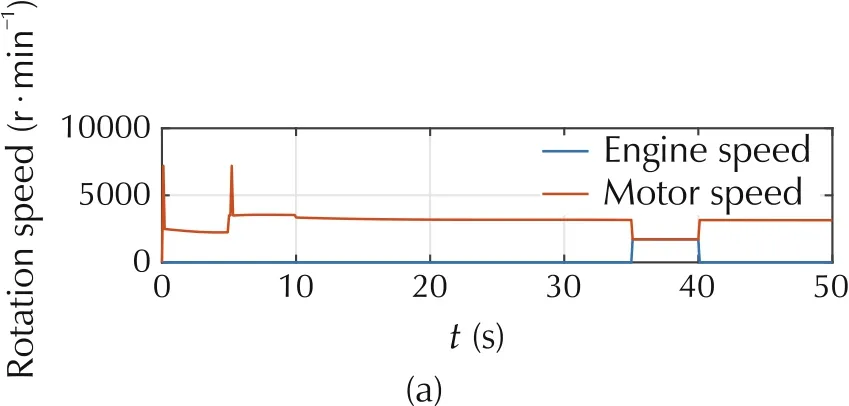
Fig.8 The speed of engine and motor for two vehicles.

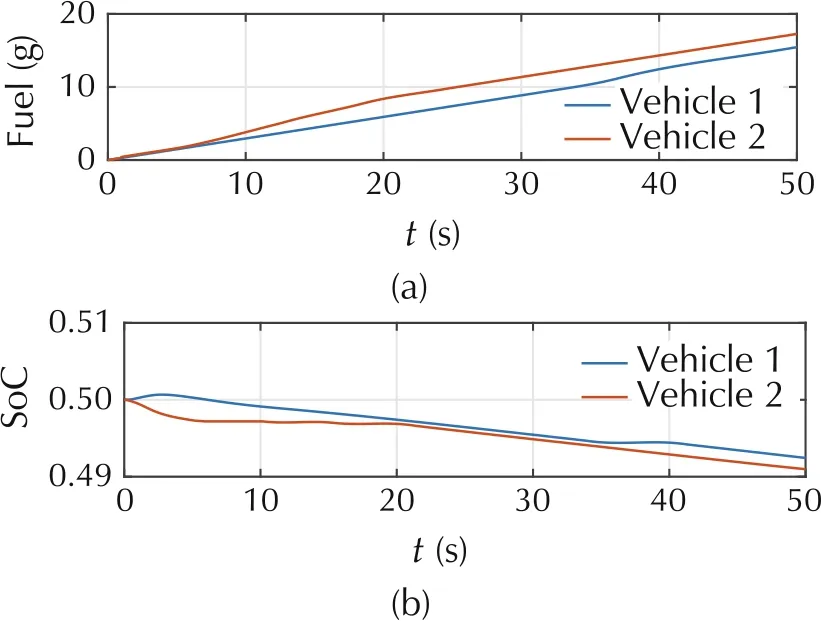
Fig.9 The fuel and SoC results for two vehicles.

Moreover, as the total energy of HEVs includes fuel and electricity, the final price of total energy consumption for the merging process is calculated as 4.8922¥of Vehicle 1 and 5.4763¥of Vehicle 2.

4 Conclusions

In this paper, a hierarchy control system which considers the energy management for automated HEVs with parallel hybrid powertrain for reasonable merging maneuver is proposed. The real-time location information and speeds of the considered vehicles are assumed to be obtained by using the advanced communication technology.In the first stage,an MPC-based optimal control problem is proposed to generate the merging trajectory.The problem is solved using C/GMRES algorithm. The first stage aims to ensure vehicles merge with a safe,smooth and cooperative process to reduce traffic jams.The calculation results of this stage provide the acceleration actions to the second stage of the control system.In the second stage, an energy management problem to optimize the power split and gear shift schedule to minimize the energy consumption is formulated under the same receding horizon. The nonlinear problem is solved using SQP method. The co-simulation is implemented in MATLAB/Simulink platform.A typical merging case is chosen to test the proposed control strategies.The results reveal that the proposed hierarchy control system can be used in the merging case for connected automated HEVs in real time.