具有变时滞随机竞争神经网络在固定时间的控制同步

蒲 浩, 冉 杰, 潘永会, 张转周, 黄建文

(1. 遵义师范学院数学学院, 贵州 遵义 563006; 2. 西南大学数学与统计学院, 重庆 400715)

自竞争型神经网络首次被提出以来, 由于竞争型神经网络模型在不同领域有重要的应用而受到广泛关注[1].近年来, 竞争型神经网络的控制同步理论[2-3]以及多重因素影响下竞争型神经网络依赖于系统初值在无限时间的控制同步问题[4-5]得到了广泛研究.Shi等[5]研究了具有不同时标和反映扩散项随机竞争神经网络实现同步的条件; Ryan[6]提出了神经网络依赖于初值在有限时间内稳定性理论; Li等[7]研究了依赖于系统初值的混合时滞和不同扰动竞争神经网络在有限时间内的同步.为了解决神经网络系统的初值事先不能准确地获得或很难获得的问题, Polyakov[8]提出了独立于系统初值的固定时间稳定性理论; Wan等[9]研究了时滞Cohen-Grossberg型神经网络的鲁棒固定时间同步.本文拟通过固定时间稳定性理论, 研究具有变时滞随机竞争神经网络在固定时间的控制同步.

1 模型及预备知识

考虑具有变时随机竞争型神经网络模型

(1)

其中n为神经元数目,p为恒定的外部刺激数目;ci为神经元时间常数;ε为短期记忆状态的时间尺度;fj(·)表示t时刻第j个神经元的输出量,xi(t)表示t时刻第i个神经元的状态;aij,bij分别表示第i个和第j个神经元之间的连接强度;τij(t)表示t时刻第i个神经元与第j个神经元之间的信号转换时滞, 满足0≤τij(t)≤τij;mil(t)表示突触效率;Hi表示外部刺激强度;αl,βi为常数.

把系统 (1) 作为主驱动系统,并引入响应系统

(2)

定义误差系统为ei(t)=yi(t)-xi(t),zi(t)=ri(t)-si(t), 根据系统(1)和系统(2)有

为实现驱动系统(1)和响应系统(2)在固定时间同步,构造外部输入控制Ui(t)=ei(t)(ki-ui|ei(t)|δ-p)/p+ei(t)(hi|zi(t)|p-vi|zi(t)|δ)/(p‖e(t)‖p)-ωiei(t)(|ei(t)|λ+|zi(t)|λ)/(np‖e(t)‖p)-εNiei(t)|ej(t-τij(t))|p/(p‖e(t)‖p), 其中ki,ui,hi,vi,ωi,Ni都是常数, 0<δ<1.

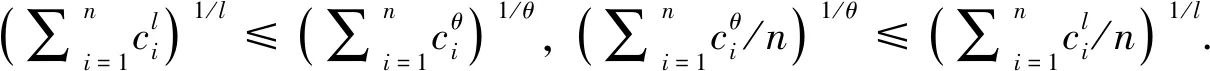
2 主要结果

定理6若(H1)(H2)成立且Xi+ki≤0,Qi+hi≤0,i∈I, 则驱动系统(1)和响应系统(2)在恰当的外部输入控制Ui(t)下, 在固定时间T=εp/[a(p-δ)]+2λ/p-1nλ/pεp/[b(λ-p)]内同步, 其中a>0,b>0,0

注1文献[11]是具有不同时标和随机扰动的竞争型神经网络, 文献[12]是混合变时滞的随机竞争型神经网络, 系统均当时间t→+∞时才能实现自适应同步.

注2在响应系统(2)中存在随机扰动项, 要使定理1中的条件Xi+ki≤0,Qi+hi≤0成立, 则需要外部输入控制Ui(t)中的ki,hi的绝对值变得更大, 故随机扰动项的存在对神经网络在固定时间的同步有抑制作用.

注3文献[13]是依赖于系统初值的混合时滞竞争型神经网络在有限时间内的同步问题,由推论1可知, 文献[13]中的结论是本文中的一种特殊情况.