余弦广义Padé逼近法及其在强非线性振子周期解求解中的应用

李震波， 唐驾时

(1.南华大学 数理学院，湖南 衡阳 421001；2.湖南大学 机械与运载工程学院，长沙 410082)

近年来，非线性振动系统的定量研究一直是学者们研究的热门课题。随着计算机技术的发展和对自然界认识的不断加深，对振动系统的定量研究逐步从弱非线性上升到了强非线性，并相继提出了很多有效的定量研究方法，如椭圆函数摄动法[1]、椭圆函数Lindsted-Poincare法[2-3]、非线性时间变换法[4-7]、同伦分析法[8-10]、变分迭代法[11]以及摄动-增量法[12]等。此外，利用Padé逼近来求解强非线性振子同、异宿轨也取得了一些成果。Emaci等[13]基于如下的经典Padé逼近式，构造了非线性薛定谔方程的同宿解。

(1)

由于经典Padé逼近式形式固定，在求解某些非线性振子时，精度不理想。因此，学者们在经典Padé逼近式的基础上进行了改进，构造了类Padé逼近式，有效地提高了求解精度。如Mikhlin在文献[14]中构造了如式(2)所示的一类同时含有多项式函数和指数函数的类Padé逼近式，并基于该类Padé逼近式求解了非线性薛定谔方程、洛伦兹方程以及Duffing方程的同宿解。

(2)

(3)

张琪昌等在文献[15-16]中提出了一种改进的类Padé逼近方法，用指数函数代替了式(2)中的多项式函数，构造了如式(3)所示的类Padé逼近式，并求解了具有立方非线性的Duffing系统同、异宿解。上述各种类Padé逼近虽然对逼近式的形式做出了各种改进，但却没有对Padé逼近的定义做出推广，而且已有的各类Padé逼近式本身均为非周期函数且通常在无穷远处存在极限。因此，从现有的文献来看，没有直接利用Padé逼近来求解微分方程周期解的相关报道。

李震波等在文献[17]中提出了一种广义Padé逼近方法，该方法将经典Padé逼近式的分子和分母由多项式函数推广至任意连续函数构成函数级数，该推广不仅从理论上统一了现有的各种Padé和类Padé逼近，也为构造更多广义形式的Padé逼近式来逼近微分方程的周期解提供了思路和方法。本文正是基于广义Padé逼近方法，构造了一类新形式的广义Padé逼近式。该逼近式的分子和分母均为余弦函数构成的函数级数，其本身具有周期性，利用该式来直接逼近一个表达式未知但幂级数形式已知的周期函数，如强非线性振子的周期解，取得了较理想的逼近结果，不仅得到了被逼近函数的高精度解析表达式，同时也较准确的预测了周期，从而扩大了Padé逼近方法在振动领域中的适用范围。总的来看，该方法具有以下特点：① 继承了Padé逼近方法求解过程简单直接的优点，便于进行计算机编程计算；②所得之解的精度不受非线性项系数大小和初始振幅大小的影响，适用于强非线性；③ 该方法并不局限于某一个特定的系统，而是有着较广的适用范围。因此，对于广义Padé逼近方法的研究和推广具有一定的实际意义和理论价值。

1 一类新的广义Padé逼近式

早在1821年，Cauch就提出了Padé逼近的理论。由于在计算数学、量子力学、量子场论、原子和分子物理及控制理论等领域中有重要应用，Padé逼近自20世纪70年代以来在理论、方法及应用上得到了很大的发展，出版了许多专著[18-20]。Padé逼近方法是从幂级数出发获得有理函数逼近式的一种十分简洁而且非常有效的方法。其基本思想就是对于一个给定的形式幂级数，构造一个有理函数，称其为Padé逼近式，使其Taylor展开有尽可能多的项与原来的幂级数相吻合。在经典Padé逼近理论的基础上，李震波等提出了一种广义Padé逼近方法，首先定义如下记号

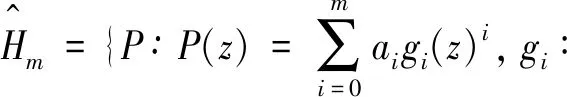
(4)

(5)

定义1(广义Padé逼近) 设f(z)为由下述形式幂级数所定义的函数

若存在有理分式函数PL(z)/QM(z)∈G(L,M)满足

f(z)-PL(z)/QM(z)=O(zL+M+1)

(6)

则称PL(z)/QM(z)为f(z)在G(L,M)中的广义Padé逼近式，记为GPA[L/M]f(z)，或简记为GPA[L/M]。

与经典Padé逼近定义相比，定义1将PL(z)和QM(z)由多项式函数推广至任意函数组成的函数级数，使得在构造广义Padé逼近式时具有更广泛的选择范围，也使得经典Padé逼近定义更完备，扩大了Padé逼近的适用范围，从理论上统一了现有的Padé和各种类Padé逼近方法。当选取PL(z)和QM(z)为多项式函数时，广义Padé逼近退化为经典Padé逼近。众所周知，经典Padé逼近式由于本身为非周期函数且通常在无穷远处存在极限，因此，从现有的文献来看，没有直接利用Padé逼近来求解微分方程周期解的相关报道，然而定义1的提出，为构造周期性的广义Padé逼近式提供了新的思路和方法，基于该定义，我们通过引入余弦函数，构造了如下形式的广义Padé逼近式

(7)

式中：α2i和β2i为待定的广义Padé系数；ω为广义Padé角频率，周期为π/ω。利用上式来逼近微分方程的周期解，取得了较理想的逼近结果，详见下文的求解和算例。

2 强非线性自治振子的周期解

考虑如下形式的自治振动系统

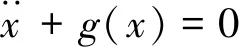
(8)

当g(x)为非线性函数时，上述方程需要利用摄动法求解，但摄动法的不足之处在于只能求解弱非线性的情形。当g(x)为高阶多项式函数或有理函数时，求解上述方程的周期解仍然是非常值得研究的课题。为此，本文基于广义Padé逼近方法，研究了当g(x)为任意非线性函数时，式(8)的周期解。

用如下形式的幂级数来表示式(8)的解

(9)

将式(9)代入式(8)，即可求得上述幂级数解的前N项系数关于初值的表达式。令周期轨道与x轴的交点为初值点，即a0=a，a1=0。则幂级数解的系数ai可表述为如下形式的代数多项式

a2n=Pn(a0,cm),a2n+1=0,n≥0

接下来要利用上述幂级数的解来确定广义Padé逼近式(7)的系数α2i和β2i。由于广义Padé角频率ω未知，若直接利用Padé逼近方法，容易造成求解困难。因此，本文在构造了一类新的广义Padé逼近式的同时，也对经典Padé逼近方法的步骤进行了相应的改进，使之更有效的逼近一类强非线性振子的周期解，并较准确的预测了周期。

以求解初值为a0=a，a1=0的周期轨为例，该方法的具体步骤如下：

步骤1令广义Padé角频率ω为主动变量，而不再是未知数，其增量为Δω。

步骤2根据经典Padé逼近的方法，将式(7)右端在原点处泰勒展开，与式(9)中的同阶项进行比较，从中得到如下形式的L+M+1个方程

Hk(α2i,β2i;ω0+Δωn,a0)=0

(10)

式中：α2i和β2i为待定的广义Padé系数；a0为所求周期轨的初值；n为迭代次数；ω0为ω的迭代初值。

步骤3根据具体情况设置ω0的值(也可直接从零开始迭代)，并根据所求结果的精度要求设置增量Δω的值，通常情况下可令Δω=0.000 1。设置好ω0和Δω的值后，代入式(10)，并迭代求解α2i和β2i，每迭代一次可得一组解。

步骤4确定目标函数，即何时终止迭代。由于求解过程中选取的初值点为周期轨道与x轴交点，则当轨道到达与x轴的另一个交点时，正好经过半个周期，即π/2ω。令该周期轨道与x轴的另一个交点为B(b0,0)，则b0可由式(11)确定

(11)

将t=π/2ω代入式(7)可得其值为α0，因此令如下函数为目标函数

Z=α0-b0

(12)

将第三步所求得的α0代入式(12)，若使得Z<1×10-N(N∈Z+为精度控制指数)，则当次迭代所求得的α2i和β2i为该周期轨道的广义Padé系数，代入式(7)即得其广义Padé解，周期T=π/(ω0+Δωn)(其中n为迭代次数)；否则，继续迭代。我们称上述方法为第一类改进的广义Padé逼近方法。

通过对Padé逼近方法的求解过程进行上述改进，可较理想的求得g(x)为多项式函数时系统式(8)的周期解。然而当g(x)为有理函数时的，对于部分周期较大的周期轨，上述方法所得之结果不能令人满意，因此我们对上述求解过程进行了再一次改进，通过引入新的目标函数并对求解结果进行分段描述等手法，得到了当系统式(8)为对称有理振子时的高精度周期解。其具体步骤为：

步骤1仍然令广义Padé角频率ω为主动变量且以ω0为初值，Δω为增量；并利用相同的方法得到式(10)。

步骤2将t=π/2ω代入式(7)可得其值为α0，因此令

α0=b0

(13)

其中b0可由式(14)确定

(14)

步骤3令如下函数为目标函数

(15)

h(0,c0)-h(a0,0)=0

(16)

步骤4将相关数据代入式(10)并进行迭代求解。将每次迭代所求得的α2i和β2i代入目标函数式(15)进行判别，若使得Z<1×10-N(N∈Z+为精度控制指数)，则当次迭代所求得的α2i和β2i为该周期轨道的广义Padé系数，并将其表述出如下分段函数即得其广义Padé解，周期T=π/(ω0+Δωn)(其中n为迭代次数)；否则，继续迭代。

(17)

通过对广义Padé逼近方法的上述二次改进，可求得系统式(8)为对称有理振子时的高精度周期解，扩大了该方法的有效范围，算例证明如下。

3 算 例

3.1 Helmholtz-Duffing振子的周期解

考虑如下形式的Helmholtz-Duffing振子

(18)

当c2c3=0时，该振子的周期解可用椭圆函数进行精确描述；本文则仅讨论c2c3≠0时的情形。首先，令式(18)的幂级数为式(9)所示，将式(9)代入式(18)即可求得式(9)的各项系数为

⋮ ⋮

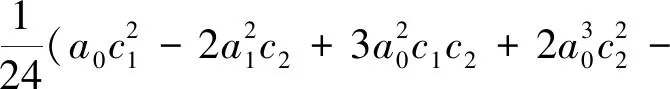
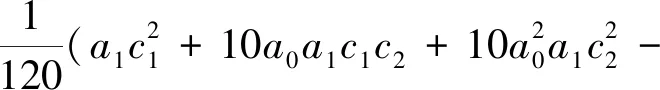
其中初值a0=a，c1=0。当系统参数c1=-2，c2=-5和c3=10时，令初始角频率ω0=0，增量Δω=0.000 1；令逼近式(7)中的L=M=3，式(12)中的精度控制指数N=6，即可利用第一类改进的广义Padé逼近方法来逼近幂级数解式(9)。当初值a=1时，求得广义Padé角频率ω=1.133 8，周期T=2.770 8，逼近式为

GPA[3/3]=(0.361 4+1.160 9cos(1.133 8t)2+

0.508 3cos(1.133 8t)4-0.007 5cos(1.133 8t)6)/(1+

2.239 1cos(1.133 8t)2-1.203 0cos(1.133 8t)4-

0.012 9cos(1.133 8t)6)

(19)

其相图如图1所示，其时间历程如图2所示，解式(19)与数值解的绝对误差曲线如图3所示，本文所采用的数值解均为四阶Runge-Kutta法所得。从图1～图3不难看出，所得之解有着较高的精度。

—表示数值解； …表示本文所得之解图1 解式(19)的相图Fig.1 The phase portrait of solution (19)

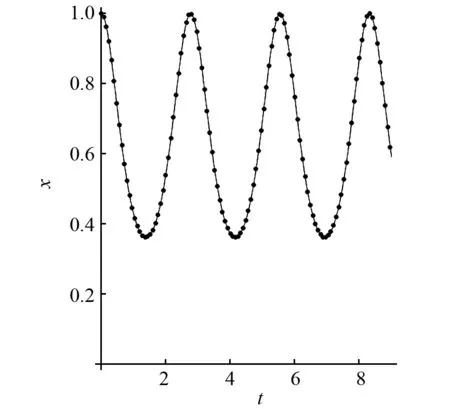
—表示数值解； …表示本文所得之解图2 解式(19)的时间历程曲线 Fig.2 Time response curve of solution (19)

图3 解式(19)与数值解的绝对误差曲线Fig.3 The absolute error curve between solution (19) and numerical solution

当初值a=-0.36时，求得广义Padé角频率ω=0.701 5，周期T=4.478 4，逼近式为

GPA[3/3]=(-0.112 3-1.182 7cos(0.701 5t)2-

1.003 6cos(0.701 5t)4-0.035 5cos(0.701 5t)6)/(1+

朝向主要考虑东南西北是个方向，东边选百叶窗、南窗配深色窗帘、西窗选有褶帘、北边选艺术窗帘。当建筑本身处于不规则形状，使得窗户所在位置不是以上四个朝向时，则需根据实际情况考虑。

9.201 2cos(0.701 5t)2-3.888 2cos(0.701 5t)4+

0.170 6cos(0.701 5t)6)

(20)

其相图如图4所示，其时间历程如图5所示，解式(20)与数值解的绝对误差曲线如图6所示。从图4～图6不难看出，所得之解有着很高的精度。

当初值a=1.15时，所求周期轨为大周期轨，令增量Δω=0.000 01，求得广义Padé角频率ω=0.845 25，周期T=3.716 8，逼近式为

GPA[3/3]=(-0.659 3+1.838 7cos(0.845 25t)2-

0.499 4cos(0.845 25t)4+0.185 3cos(0.845 25t)6)/(1+

1.200 6cos(0.845 25t)2-1.474 4cos(0.845 25t)4+

(21)

其相图如图7所示，其时间历程如图8所示，解式(21)与数值解的绝对误差曲线如图9所示。

—表示数值解； …表示本文所得之解图4 解式(20)的相图Fig.4 The phase portrait of solution (20)

—表示数值解； …表示本文所得之解图5 解式(20)的时间历程曲线Fig.5 Time response curve of solution (20)

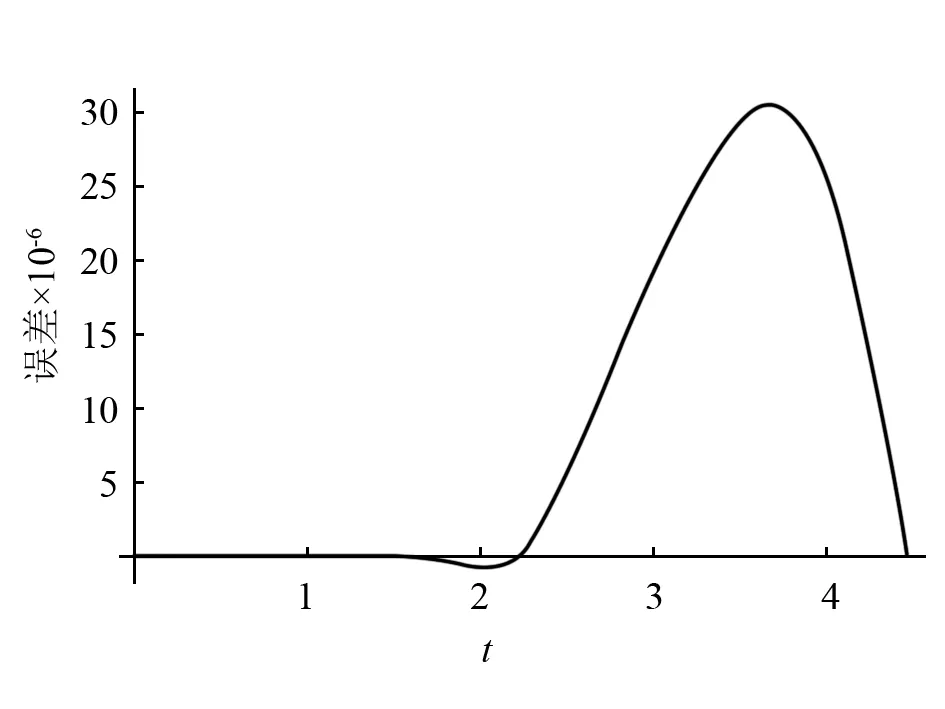
图6 解式(20)与数值解的绝对误差曲线Fig.6 The absolute error curve between solution (20) and numerical solution

—表示数值解； …表示本文所得之解图7 解式(21)的相图Fig.7 The phase portrait of solution (21)

—表示数值解； …表示本文所得之解图8 解式(21)的时间历程曲线Fig.8 Time response curve of solution (21)

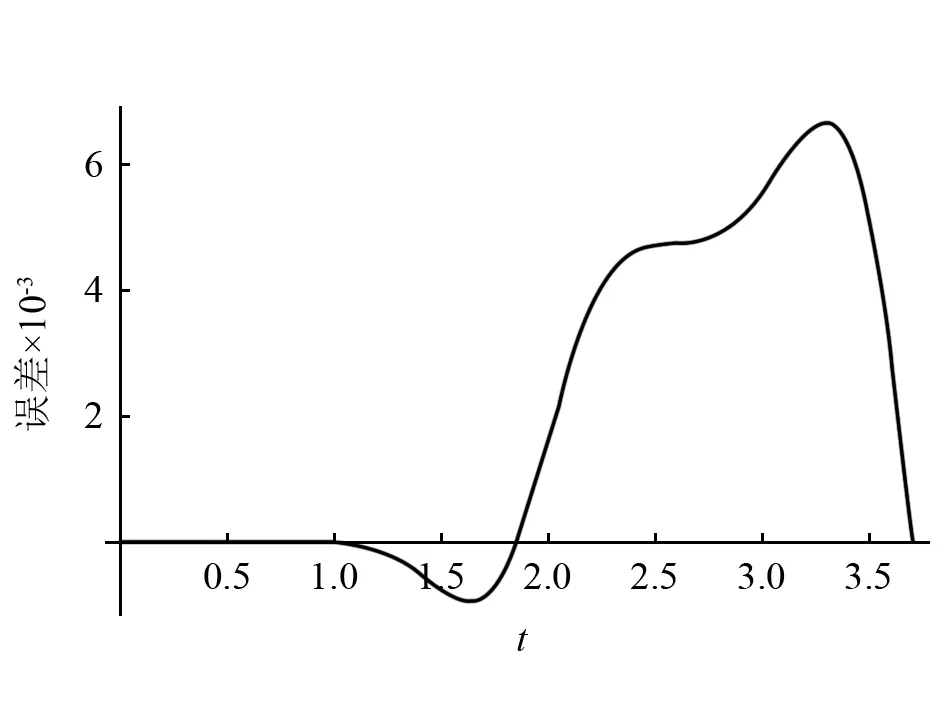
图9 解式(21)与数值解的绝对误差曲线Fig.9 The absolute error curve between solution (21) and numerical solution

接下来讨论系统式(18)在不同参数时，该方法的可靠性。表1描述了在c1，c2和初值不变，最高阶非线性项系数c3由小增大时，利用第一类改进的广义Padé逼近方法所求得的闭轨周期与数值方法得到的周期之间的关系。表2则描述了在参数不变，初始振幅由小增大时，利用第一类改进的广义Padé逼近方法所求得的闭轨周期与数值方法得到的周期之间的关系。其中T1为本文求得的周期，T2为数值方法得到的周期，Te为二者的误差。从上述二表中不难看出，该方法的误差不会随着非线性项系数的增大而增大，精度亦不随着初始振幅的增大而减小，因此该方法在强非线性和大振幅下均有较高的可靠性。

表1 系统式(18)在不同参数下的周期比较Tab.1 The comparisons of the periodic with different parameters of system (18)

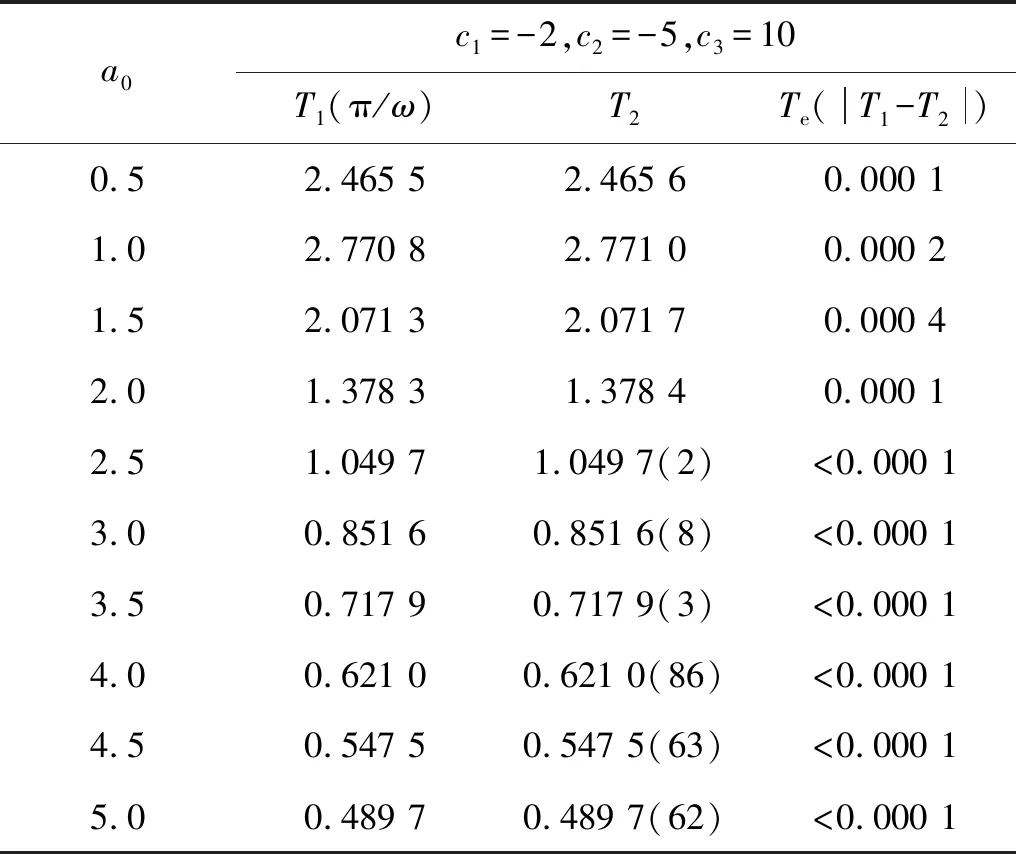
表2 系统式(18)在不同初始振幅下的周期比较Tab.2 The comparison of periodic with different initial amplitude of system (18)

3.2 广义Duffing-Harmonic振子的周期解

广义Duffing-Harmonic振子可由式(22)描述

(22)

考虑μv≠0的情形。Duffing-Harmonic振子常被用来检验一些近似求解算法的精度和有效性。本文亦选取该振子来验证改进的广义Padé逼近方法之有效性和精度。首先，令式(22)的幂级数为式(9)所示，将式(9)代入式(22)即可求得式(9)的各项系数为

⋮ ⋮

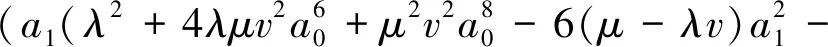
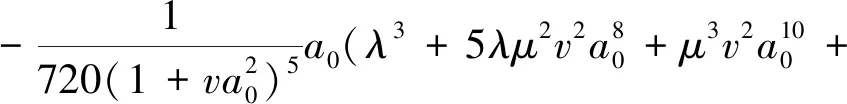
其中初值a0=a，a1=0。当λ=-1，μ=5和v=2，初值a=0.6时，仍可用第一类改进的广义Padé逼近方法来求解，令初始角频率ω0=0，增量Δω=0.000 01；令逼近式(7)中的L=M=3，式(12)中的精度控制指数N=6，求得广义Padé角频率ω=0.547 62，周期T=5.736 8，逼近式为

GPA[3/3]=(0.247 37+0.161 3cos(0.547 62t)2+

0.009 9cos(0.547 62t)4+0.013 0cos(0.547 62t)6)/(1-

0.380 7cos(0.547 62t)2+0.110 5cos(0.547 62t)4-

0.010 4cos(0.547 62t)6)

(23)

其相图如图10所示，时间历程如图11所示，解式(23)与数值解的绝对误差曲线如图12所示。从上述图像可看出，解式(23)有着较高的精度，也进一步验证了该方法的有效性。

—表示数值解； …表示本文所得之解图10 解(23)的相图Fig.10 The phase portrait of solution (23)

—表示数值解； …表示本文所得之解图11 解(23)的时间历程曲线Fig.11 Time response curve of solution (23)

图12 解式(23)与数值解的绝对误差曲线Fig.12 The absolute error curve between solution (23) and numerical solution

当初值a=0.9时，式(22)的周期轨为大周期轨，即在相图上包围了所有奇点的轨道。此时，利用第一类改进的广义Padé逼近方法所求得的结果精度不太理想，由于式(22)为对称振子，因此可采用第二类改进的广义Padé逼近方法来求解，令初始角频率ω0=0，增量Δω=0.000 001；令逼近式(7)中的L=M=4，式(12)中的精度控制指数N=6，可求得广义Padé角频率ω=0.441 812，周期T=7.110 7，逼近式为

35.690 9cos(0.441 812t)4+41.584 9cos(0.441 812t)6-

22.422 4cos(0.441 812t)8)/(1-12.535 7cos(0.441 812t)2+

15.439 6cos(0.441 812t)4-12.019 9cos(0.441 812t)6+

2.142 1cos(0.441 812t)8)

(24)

根据式(17)，将系统式(22)的解描述为如下分段函数

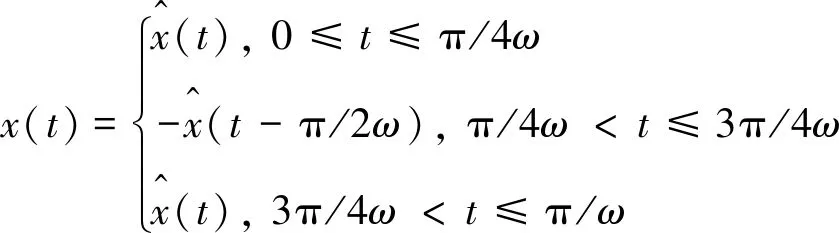
(25)

式中：ω为所求得的广义Padé角频率。其相图如图13所示，时间历程如图14所示，解式(25)与数值解的绝对误差曲线如图15所示。由上述图像可知，第二类改进的广义Padé逼近方法仍然有着较高的精度和可靠性。为进一步说明，我们绘制了相应的表格。表3描述了在λ，v和初值不变，最高阶非线性项系数μ由小增大时，利用第二类改进的广义Padé逼近方法所求得的闭轨周期与数值方法得到的周期之间的关系。表4则描述了在参数不变，初始振幅由小增大时，利用第二类改进的广义Padé逼近方法所求得的闭轨周期与数值方法得到的周期之间的关系。其中T1为本文求得的周期，T2为数值方法得到的周期，Te为二者的误差。

表3 系统式(22)在不同参数下的周期比较Tab.3 The comparisons of the periodic with different parameters of system (22)

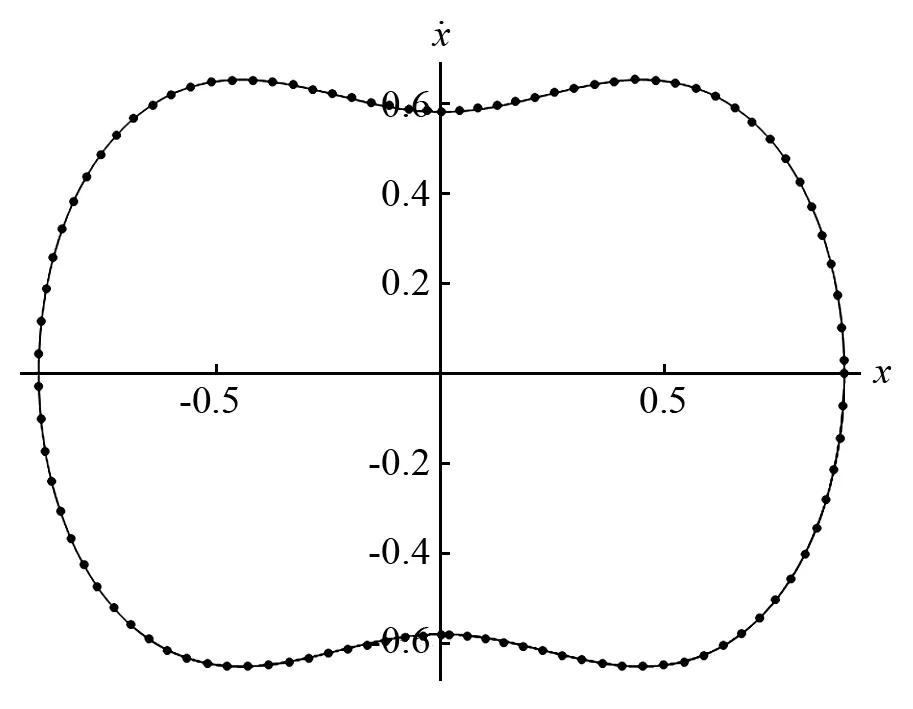
—表示数值解； …表示本文所得之解图13 解式(25)的相图Fig.13 The phase portrait of solution (25)

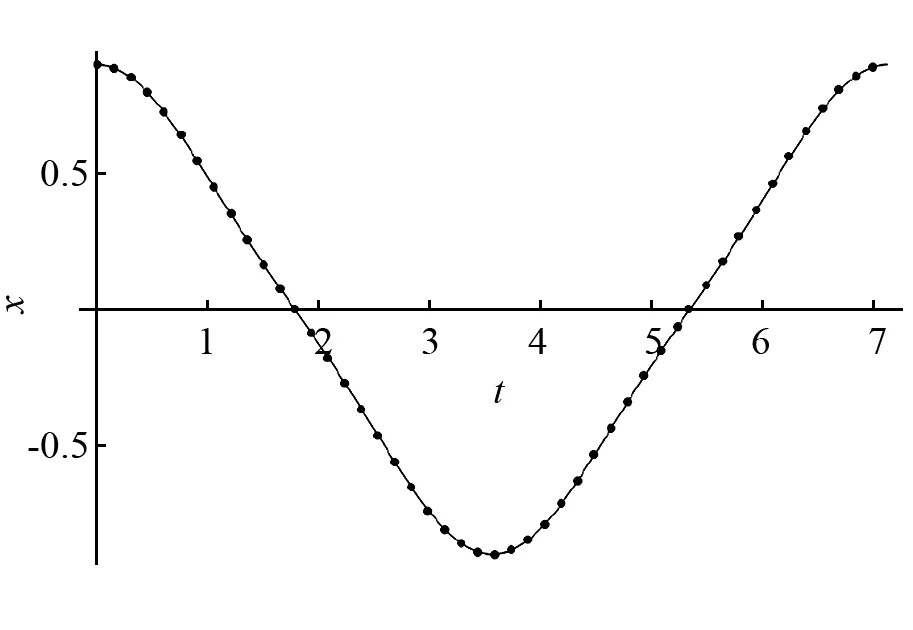
—表示数值解； …表示本文所得之解图14 解式(25)的时间历程曲线Fig.14 Time response curve of solution (25)

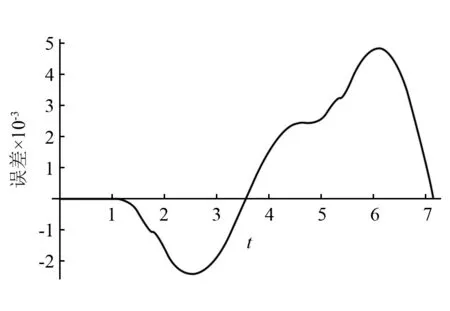
图15 解式与(25)数值解的绝对误差曲线Fig.15 The absolute error curve between solution (25) and numerical solution

表4 系统式(22)在不同初始振幅下的周期比较Tab.4 The comparison of periodic with different initial amplitudeof system (22)

从表3和表4中可见，在强非线性和大振幅下，本文所求得的广义Duffing-Harmonic振子的周期均保持着较高的精度，进一步表明了该方法的有效性和可靠性。

3.3 势能函数为无理函数的振子

本小节考虑如下形式无理振子

(26)

⋮ ⋮

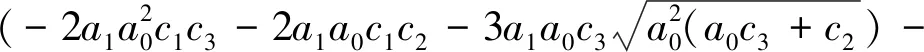
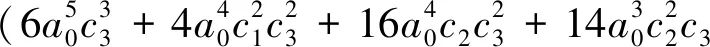
其中初值a0=a，a1=0。当系统参数c1=-2，c2=1和c3=4时，系统的大致相图如图16所示。令初始角频率ω0=0，增量Δω=0.000 01。令式中的L=M=3，式(12)中的精度控制指数N=6，即可利用第一类改进的广义Padé逼近方法来逼近幂级数解式(9)。当初值a=0.5时，求得广义Padé角频率ω=0.419 08，周期T=7.496 4，逼近式为

GPA[3/3]=(0.960 3-1.058 0cos(0.419 05t)2+

0.304 5cos(0.419 05t)4-0.018 0cos(0.419 05t)6)/

(1-0.531 4cos(0.419 05t)2-0.086 1cos(0.419 05t)4-

0.004 6cos(0.419 05t)6)

(27)

其相图如图17所示，其时间历程如图18所示，解式(27)与数值解的绝对误差曲线如图19所示。

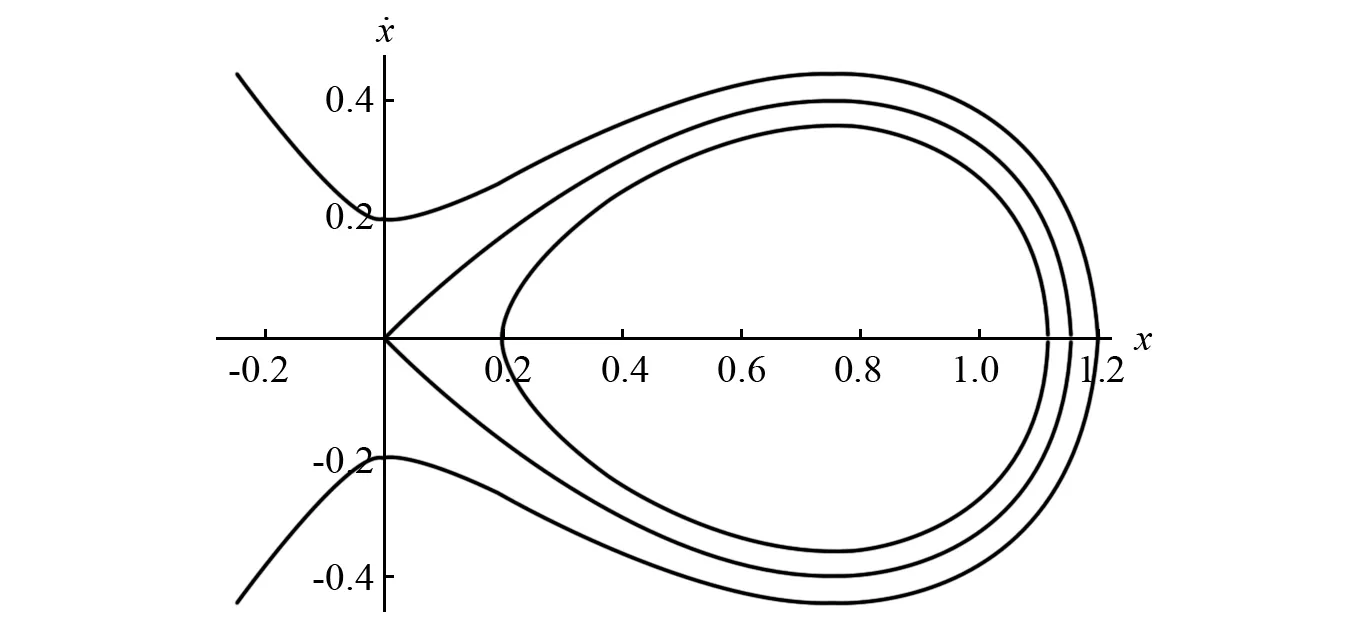
图16 系统式(26)在c1=-2，c2=1和c3=4时的大致相图Fig.16 The rough phase portrait of system (26) when c1=-2,c2=1,c3=4

从图17～图19不难看出，所得之解有着很高的精度。下面讨论系统在不同初值时，利用第一类改进的广义Padé逼近方法所求得的闭轨周期与数值方法得到的周期之间的关系。如表5所示，其中T1为本文求得的周期，T2为数值方法得到的周期，Te为二者的误差。从上表中不难看出，该方法对于不同初值的周期轨均有着较好的精度。从本小节的内容可以看出，本节提出的改进的广义Padé逼近方法在无理振子的周期解求解中依然有着较高的精度，也进一步说明了该方法有着较广的适用范围。

—表示数值解； …表示本文所得之解图17 解式(27)的相图Fig.17 The phase portrait of solution (27)

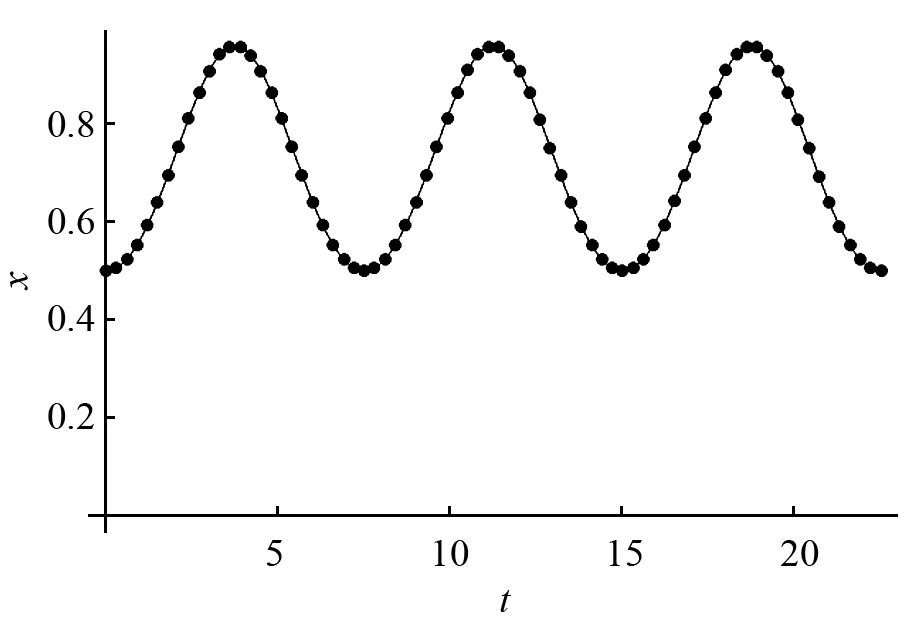
—表示数值解； …表示本文所得之解图18 解式(27)的时间历程曲线Fig.18 Time response curve of solution (27)

图19 解式(27)与数值解的绝对误差曲线.Fig.19 The absolute error curve between solution (27) and numerical solution

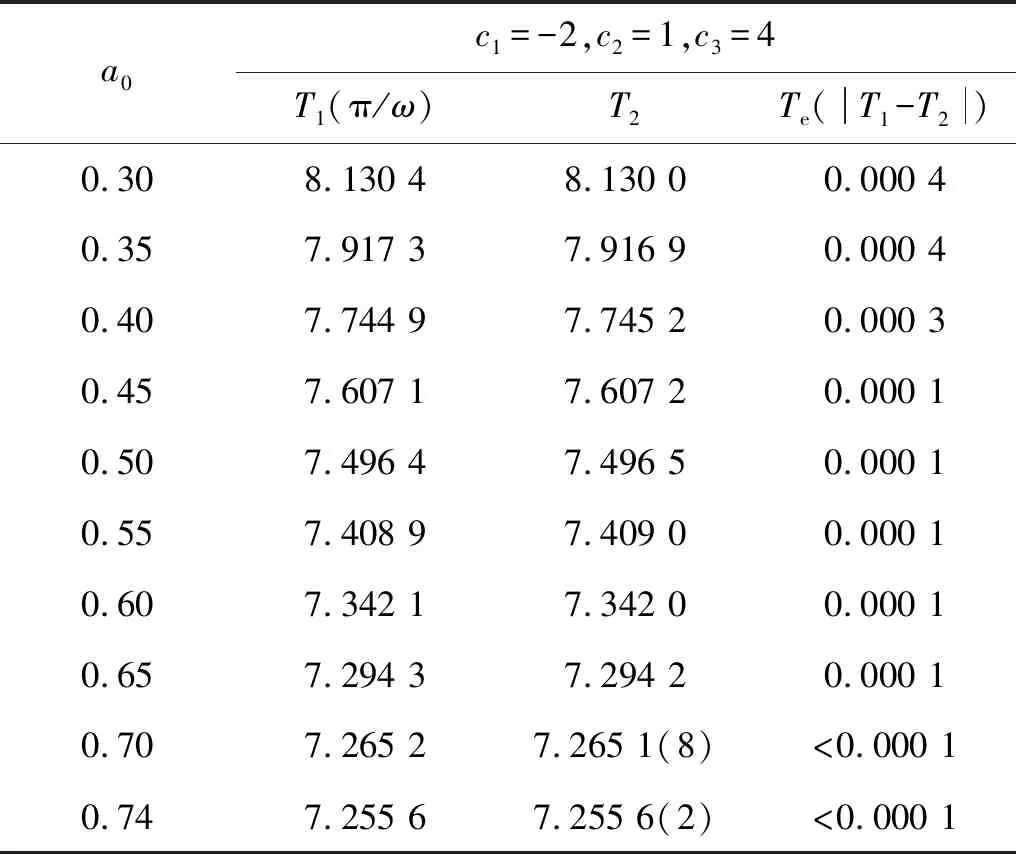
表5 系统式(26)在不同初始振幅下的周期比较Tab.5 The comparison of periodic with different initial amplitude of system (26)

4 结 论

本文基于广义Padé逼近方法，构造了一类由余弦函数级数组成的新的广义Padé逼近式；同时，对经典Padé逼近的求解过程进行了合理的改进，并求得了一类势能函数为高阶多项式、有理函数和无理函数振子的高精度解析周期解及其周期，为非线性振动的定量研究提供了新的思路和参考方法，也扩大了Padé逼近方法的适用范围，因此对该方法的研究具有一定的理论价值和实际意义。总的来说该方法具有以下特点：①继承了Padé逼近方法求解过程简单直接的优点，便于进行计算机编程计算；②在强非线性和大振幅下，所得结果均保持较高精度，保证了该方法的可靠性；③该方法并不局限于某一个固定的系统，而是有着较广的适用范围。将该方法进行进一步的改进，亦可用于求解阻尼振动和受迫振动的情形，这也将是我们下一步的工作。