一类分数阶分段光滑系统的非线性振动特性

2019-12-02申永军杨绍普温少芳王美琪

振动与冲击 2019年22期

王军，申永军，杨绍普，温少芳，王美琪

(1.石家庄铁道大学机械工程学院，石家庄 050043； 2.石家庄铁道大学交通运输学院，石家庄 050043)

近年来非线性科学研究发展迅速，其中的非光滑动力系统作为非线性动力系统的一部分，更是研究热点之一。非光滑运动广泛存在于诸多振动系统中，如车辆悬挂系统、缓冲器、振动筛、振动输送机等由于间隙的存在，均存在非光滑动力学行为，会对系统的动态特性产生不良的影响，甚至给车辆或机器带来严重的安全隐患。已有许多国内外学者投入到了非光滑动力学研究中，其中分段光滑系统的研究也取得了一些进展。卫晓娟等[1]分析了单自由度分段光滑系统由n-1周期运动经周期倍化分岔通向混沌的行为，接着对系统混沌运动的控制做出了研究。张正娣等[2]研究了非光滑Duffing振子随慢变参数变化的不同平衡点和相应的分岔行为，揭示了该类非光滑系统中不同簇发振荡的产生机理。张思进等[3]针对齿轮系统的分段线性模型，运用Melnikov理论研究了齿轮系统异宿轨道的全局分岔条件以及系统周期运动的稳定性。Li等[4]得到了分段光滑系统的次谐轨道的Melnikov函数。Huang等[5]得到了具有负刚度的受控分段光滑系统的频率响应和稳定性条件，并研究了该系统出现的对称破裂分岔和混沌运动。已有研究表明，选择合适的系统参数可以对原有动力学系统的性能进行提升，比如可以避免振幅的跳跃、改变系统的分岔行为以提高系统工作的稳定性[6-9]。

对于黏弹性材料如车辆悬挂系统中的元器件磁流变阻尼器、油压减震器等，若单纯地考虑其弹性特性或阻尼特性而建立的模型并不能完全反映材料本质。和整数阶相比，分数阶模型能够更好地描述材料的黏弹性，更能准确地描述一些物理变化过程和非线性特性。其实，整数阶微积分仅是分数阶的一个特例，是一种理想化的形式。因此，以分数阶微积分模型来优化传统的整数阶模型会更加准确，更能反映系统的本构关系。相关研究也表明采用分数阶微积分建立的模型更准确，更能描述实际系统的动态特性。如孙会来等[10]引入分数阶导数建立了油气悬架的模型，并通过数值及实验验证了分数阶模型比整数阶模型能更精确地描述油气悬架的特性。Lewandowski等[11]采用分数阶模型对黏弹性阻尼器进行了描述，通过理论分析了该类阻尼器的设计敏感性，并举例进行了验证。李占龙等[12]提出了基于FKV本构的黏弹性悬架分数阶减振模型，并用数值方法得到了这种黏弹性悬架响应具有全局相关性和记忆性。吴杰等[13]以橡胶隔振器为研究对象，给出了隔振器的分数阶动力学模型，并与传统模型进行了对比分析，结果表明含有分数导数的模型能够较好地预测橡胶隔振器的动态特性。

在振动力学方面，正是由于分数阶模型表现出来的这些良好的特性，使得更多的学者致力于分数阶模型的振动特性研究。Shen等[14-16]采用平均方法研究了不同分数阶微分振子的动力学行为，发现分数阶微分项不仅起线性阻尼的作用，还可以等效为线性刚度。Xu等[17]结合L-P方法和多尺度方法提出一种新的方法求解分数阶Duffing振子的二阶近似解，并采用蒙特卡洛方法分析了该系统的动力学特性。Chen等[18]采用随机平均法对一个分数阶微分振子的统计响应做出了研究，得到了一些统计指标如条件可靠性函数和条件概率密度函数等。Xiao等[19]采用谐波平衡法建立了分数阶Vander Pol 振子周期解的近似表达式。对于求解一次近似解的多种分析方法来说，平均法是一种处理分段系统更为成熟、更为直观的方法，故本文采用该方法对分数阶和分段光滑系统进行研究。

但是目前对于分段光滑分数阶系统的研究还比较少，而且多采用数值方法进行研究，在现有的文献中，Wu等[20]采用数值方法研究了一个分数阶分段线性系统，发现了不动点、周期运动和混沌运动等丰富的动力学行为，提出了基于分数阶滑模控制的混沌同步控制策略。Lu[21]对含分数阶的分段线性蔡氏电路的混沌行为进行了分析，发现奇次分数阶蔡氏电路发生混沌的最小阶次是2.7，非齐次分数阶蔡氏电路发生混沌现象的最小阶次为2.8。

通过以上文献可以看出，现有研究多偏重于单独的分段光滑系统或单独含分数阶微分项系统的动力学理论研究，关于分数阶和分段光滑耦合作用下系统动力学特性的研究还很少。在含有分数阶的分段光滑系统中，由于分数阶和分段光滑系统非线性的双重影响，其动力学行为的理论分析变得更加复杂，对于系统的周期解及其稳定性和系统参数对动力学性能的影响等很多问题还需要深入的研究。

本文以含间隙的分数阶分段光滑碰撞振子为研究对象，将其简化为一对称的分段光滑模型，采用平均法获得系统的周期解，并对其幅频曲线的稳定性和跳跃现象进行研究，其次分析分段参数和分数阶参数对系统振动性能及稳定性的影响，最后对分岔方程进行奇异性分析，得到系统的转迁集和分岔图。

1 系统动力学模型及近似解

图1为含对称间隙的分数阶弹性碰撞振子，当振幅小于间隙δ时，只有主弹簧-阻尼系统起作用，系统作线性振动；当振幅大于间隙δ时，振子和副弹簧-阻尼系统反复接触后又分离，系统呈现非线性振动，系统的动力学方程可写为

式中:m为振子质量;k1f1(x)，c1f2(x)分别为分段光滑的弹簧力和阻尼力；KDp[x(t)]为分数阶微分项;F为激振力，其中，

(2)

(3)

引入参数

原式(1)可变为

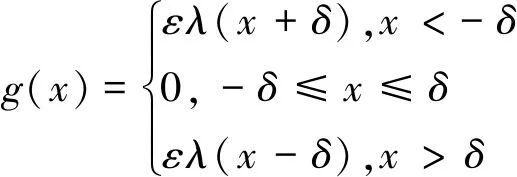
(5)

式(4)可变为

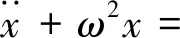
2μ1f2(x)-K1Dp[x(t)]]

(6)

设式(6)的解为

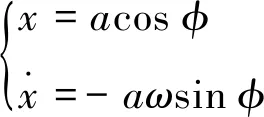
(7)

式中:φ=ωt+θ，则根据平均法可以得到

(8)

式中:δ=acosφ0。

(9)

图1 单自由度分数阶分段光滑系统Fig.1 A single-degree-of-freedom piecewise smooth system with fractional-order derivative

式(8)第一部分P1的积分代表系统光滑的部分，第二部分P2的积分代表了系统非光滑的部分，第三部分P3的积分是分数阶项的积分，这里采用分数阶的Caputo定义对分数阶微分项进行计算，形式为

(10)

这里Γ(z) 是Gamma函数满足Γ(z+1)=zΓ(z)。可求得

(11)

其中，

(12)

式(12)代入原参数整理得到

(13)

(14a)

(14b)

C(a)，K(a)分别为系统的等效刚度和等效阻尼，由式(14)可知，等效刚度和阻尼均是由三部分组成。第一部分k1和c1分别为系统的主刚度和阻尼；第二部分k2H(a)和c2H(a)项分别为分段刚度和分段阻尼对系统的等效值，当a≤δ时，这部分为零，当a>δ时，这部分值的大小取决于分段刚度k2和分段阻尼c2，同时由于H(a)是振幅a的函数，且含参数δ，因此它的大小也受分段间隙δ和系统振幅a的影响；第三部分为分数阶部分，显然，分数阶部分的大小取决于分数阶系数K1和阶次p。

2 数值仿真

选取系统参数m=10，c1=1，c2=2，F=3，k1=10，k2=15，δ=0.5，K1=0.1，p=0.5，根据式(13)画出幅频曲线，图2中用实线表示。

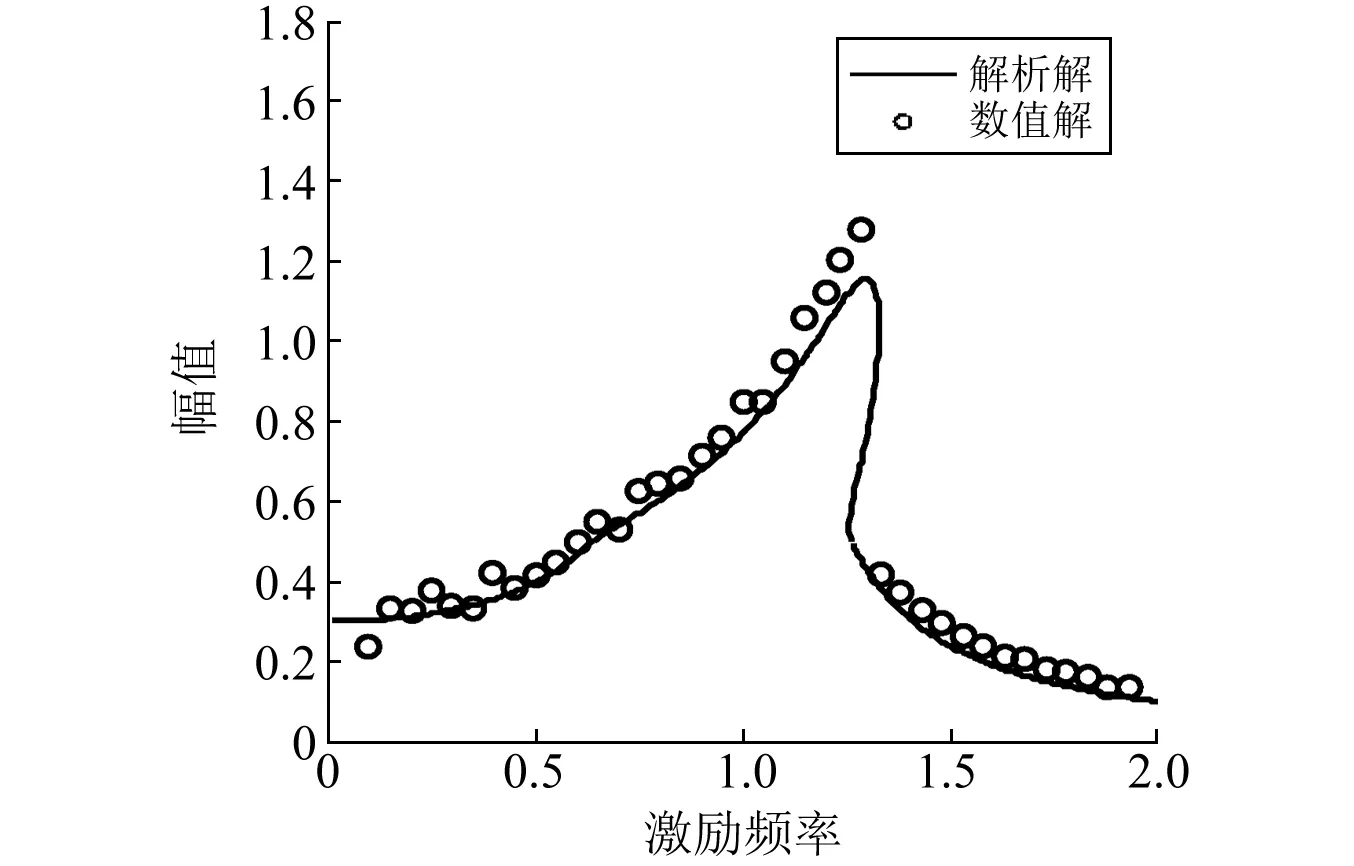
图2 近似解和数值解对比图Fig.2 Comparison of the solutions by analytical and numerical methods

为了验证近似解的正确性，这里采用了文献[22-23]里介绍的幂级数法进行数值研究，该数值方法的近似公式采用

(15)

(16)

3 稳态解及稳态解的稳定性分析

对于分段光滑的非线性系统，本文重点研究的是振子受迫振动的稳态周期响应，因此令

消除变量θ，求得系统稳态周期解的幅频响应方程为

(17)

当a≤δ时系统为线性频响特性，因此只考虑a>δ的情况。

(18)

(19)

由式(19)得到特征方程为

(20)

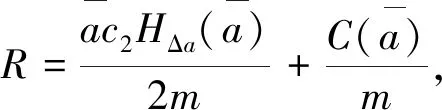
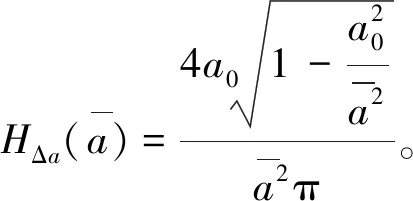
通过R，Q可以判断周期解的稳定性，由于阻尼均为正，R≫0，所以，特征值不可能出现一对纯虚根，不会发生霍普夫分岔，我们只讨论R>0的情况，为了方便观察，画出Q=0的曲线，用虚线表示。

(1)Q≫于0，幅频曲线和Q=0的曲线没有交点。即幅频曲线上的所有点均满足Q>0，如图3所示，此时没有出现多解现象，周期解是稳定的。

(2) 随着非线性的逐渐加强，幅频曲线和Q=0曲线出现了交点，当只有一个交点时，处于跳跃的临界状态，当非线性继续加强，出现两个交点时，如图4所示，幅频曲线和曲线Q=0在A，B处相交，周期解的稳定性在交点处发生了变化，出现了鞍结分岔现象(交点A，B在幅频曲线处有垂直切线)，A，B点即为稳定区和不稳定区的分界点。在Q=0曲线以外，幅频曲线上的点均满足Q>0，为稳定的周期解，而在Q=0曲线以内，幅频曲线上的点使得Q<0，因此为不稳定的周期解。

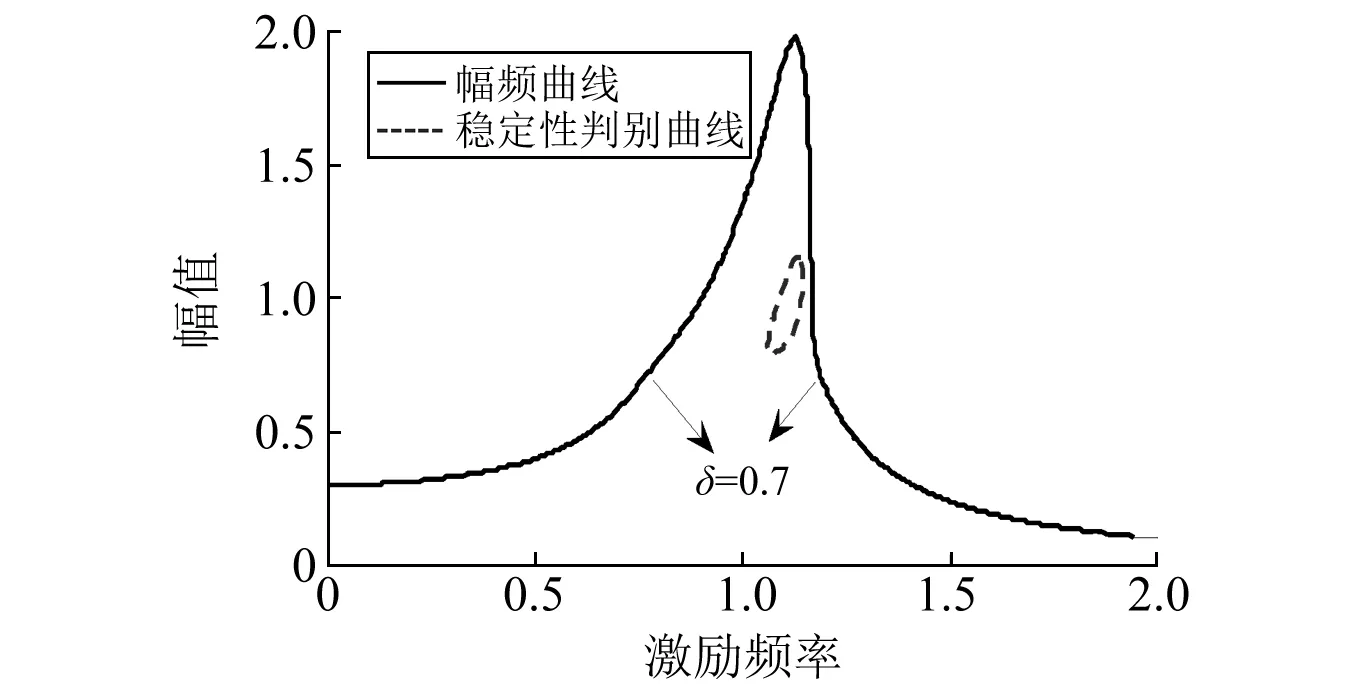
注：m=10；c1=1；c2=0.5；F=3；k1=10；k2=5； δ=0.7；K1=0.1；p=0.5图3 系统稳态解的幅频曲线和不稳定区域(无交点)修改Fig.3 The amplitude-frequency curve and its stability region for the steady-state solution (no intersection)

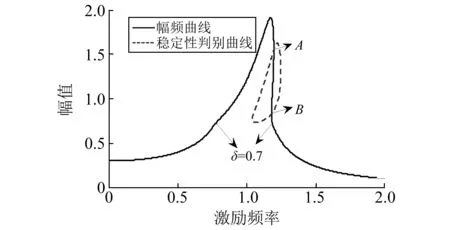
注：m=10;c1=1;c2=0.5;F=3;k1=10；k2=7； δ=0.7；K1=0.1；p=0.5图4 系统稳态解的幅频曲线和不稳定区域(有交点)Fig.3 The amplitude-frequency curve and its stability region for the steady-state solution (have intersections)

跳跃现象的产生正是由于存在着这种不稳定区域。出现跳跃时系统参数需满足幅频曲线相对于纵轴的斜率存在为零的点，即

(21)

对于分段光滑系统，在分段点δ处也可能出现分岔现象，当幅频曲线对a的偏导在分段点δ处等于零时，B点和δ点重合，如图5所示，即在δ处发生了鞍结分岔，系统参数需要满足以下的关系

P=2{ω2C2(δ)+[mω2-K(δ)]2}+

δHΔa(δ){ω2c2+2k2[mω2-K(δ)]}=0

(22)

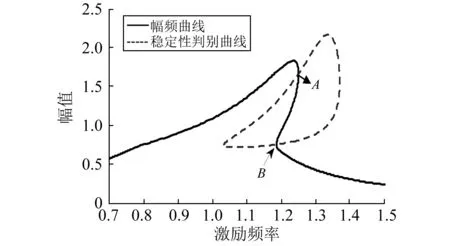
注：m=10；c1=1；c2=0.5；F=3；k1=10；k2=30； δ=0.7；K1=0.1;p=0.5图5 分段点发生鞍结分岔Fig.5 Saddle node bifurcation at the segmentation point

而当曲线Q=0和幅频曲线相交于分段δ处，且P不等于零时，这时只有A点为鞍结分岔点，B点则为非光滑系统特有的擦边分岔[24]，由于系统的幅频曲线是由a<δ的线性部分和a≥δ部分的非线性曲线拼接而成的，因此在分段点处形成了尖角。如图6所示。

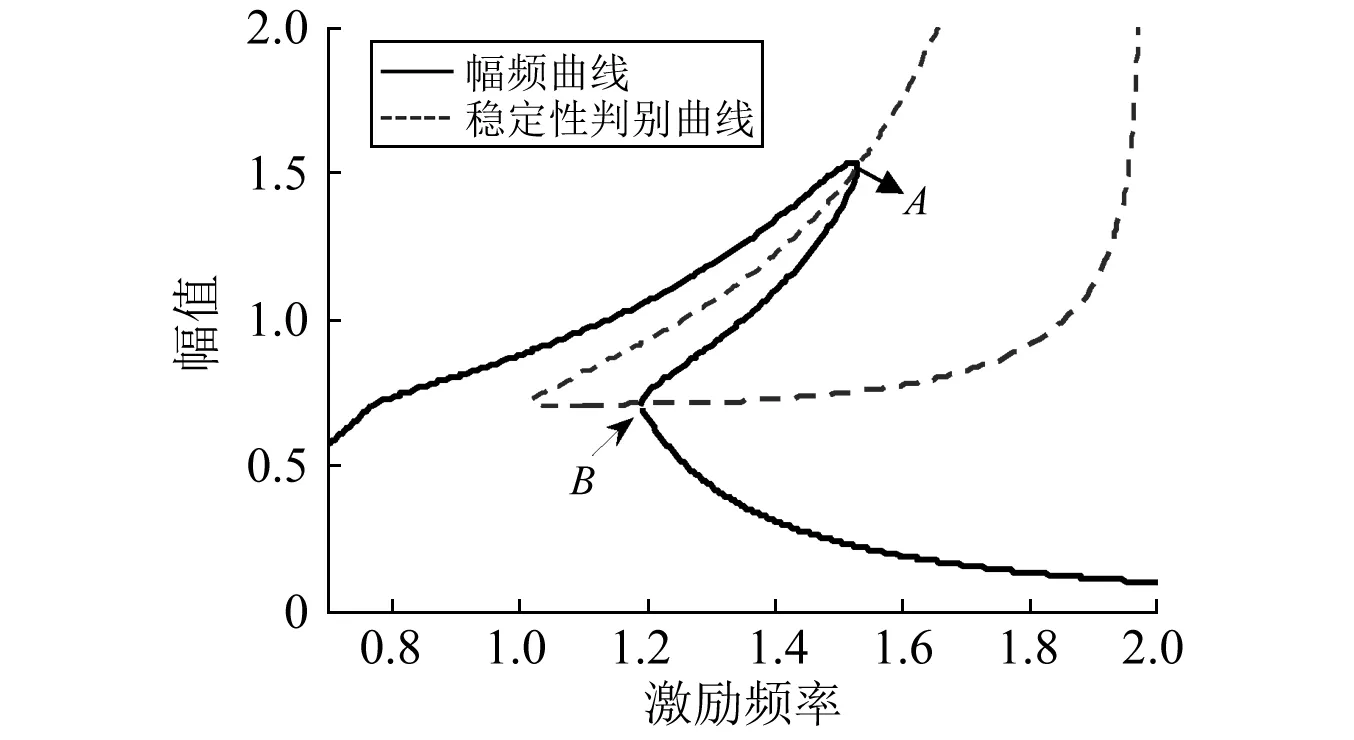
注：m=10;c1=1;c2=0.5;F=3;k1=10;k2=30; δ=0.7;K1=0.1;p=0.5图6 分段点发生擦边分岔Fig.6 Grazing bifurcation at the segmentation point

4 参数分析

通过Q，R可以判别周期解的稳定性，系统的幅频响应曲线在不稳定区域会发生跳跃，这种跳跃现象的产生正是由于存在不稳定区域，因此，设计系统时，应当避免这种不稳定区域的出现，或者减小不稳定区域。以下讨论系统参数对不稳定区域和系统动力学特性的影响。由于系统参数较多，假设其它参数不变，首先分析分段刚度及分段阻尼对系统稳定性和动力学的影响。

图7为分段刚度变化时系统的幅频曲线和稳定性曲线Q。当k2=5时，曲线Q和幅频曲线没有交点，幅频曲线没有出现多解现象，此时幅频曲线是渐进稳定的，k2=7时，判定条件Q曲线的范围加大，即不稳定区域增大，被Q曲线围起来的部分即为周期解的不稳定区间，其余处于Q曲线外部的部分是渐进稳定的，交点为稳定点，而非渐进稳定点，当k2进一步加大到9时，Q曲线的范围也进一步增大，不稳定区域变得更大，同时，不稳定周期解的范围也加大。另一方面，随着非线性刚度k2的增大，共振区域也发生变化，系统共振频率明显加大，振幅峰值逐渐减小，振幅滞后现象愈发明显，系统的非线性随着弹簧刚度k2的增大而加强。

注：m=10;c1=1;c2=0.5;F=3;k1=10;k2=5,7,9; δ=0.7;K1=0.1;p=0.5图7 分段刚度对幅频曲线及其不稳定区域的影响Fig.7 Effects of the piecewise stiffness k2 on the amplitude-frequency curves and their unstable regions

图8为分段阻尼c2分别取1，3，5，7时，系统幅频曲线的变化图，从图中我们可以看出，随着分段阻尼c2的增大，系统的非线性特性并没有大的变化，共振区的频率范围也几乎没有变化，但是系统的振动幅值明显减小，共振频率随着分段阻尼c2的增大也逐渐减小，从图3还可以看出，系统的不稳定区域随着c2的增大也逐渐减小，达到一定值时，系统频响曲线不再发生跳跃现象，不稳定区域消失。因此，可以通过加大分段阻尼c2来抑制系统不稳定区域的产生。

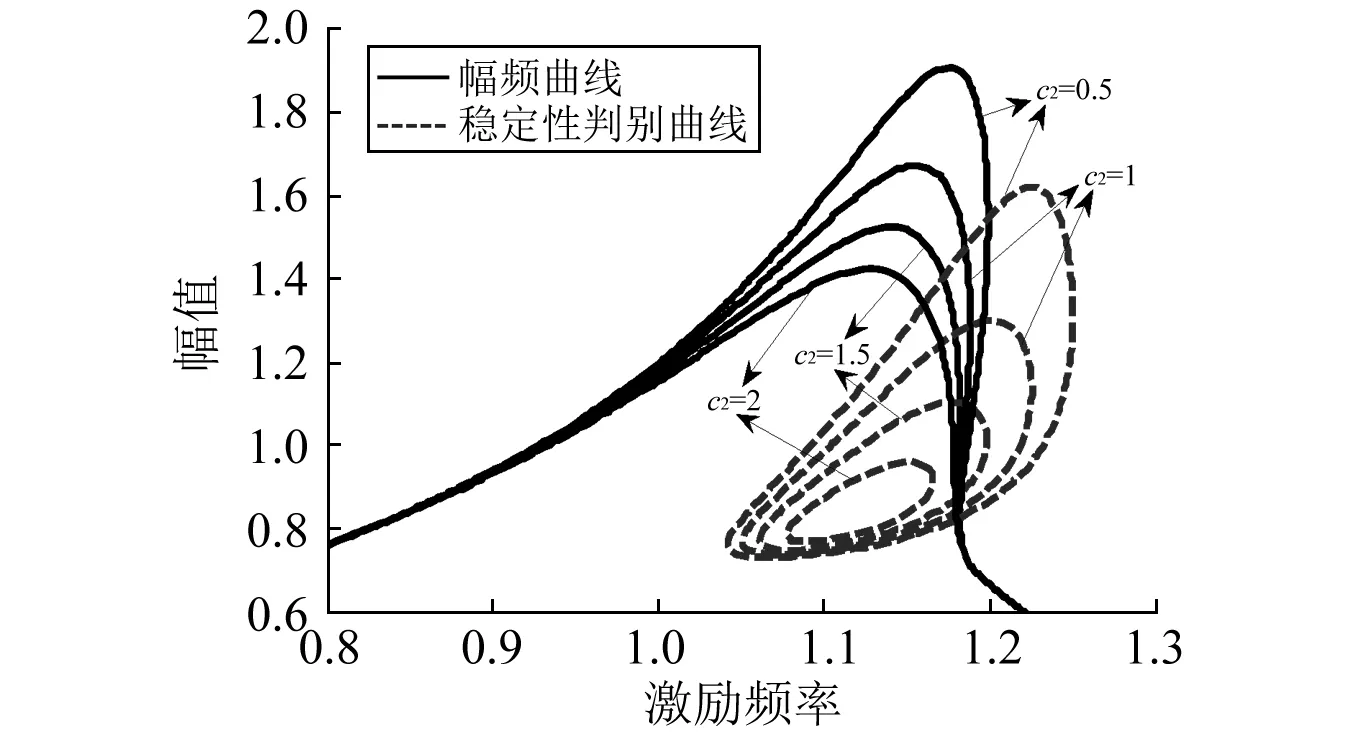
注：m=10;c1=1;c2=0.5,1,1.5,2;F=3;k1=10; k2=7;δ=0.7;K1=0.1;p=0.5图8 分段阻尼对幅频曲线及其不稳态区域的影响Fig.8 Effects of the piecewise damping c2 on the amplitude-frequency curves and their unstable regions

其次，分析分数阶系数K1和阶次p对系统振动和稳定区域的影响。保持其它参数不变，分数阶系数K1分别取0.1，0.5，0.9时，系统幅频曲线及稳定性判别曲线如图9所示。显然，当K1逐渐增大时，系统的非线性特性逐渐增强，且由式(14)可知，随着K1的增大，系统的等效刚度逐渐增大，因此系统的共振幅值逐渐减小，同时，由于阻尼也随着K1的增大而逐渐增大，导致系统共振频率随之逐渐增大，然而，共振区的频率范围却随着K1的增大而逐渐缩小。同样由图9可以看出，幅频曲线的不稳定性区域随着K1逐渐增大而逐渐减小。

注：m=10；c1=1；c2=0.5；F=3；k1=10；k2=7；δ=0.7； K1=0.1,0.5,0.9；p=0.5图9 分数阶系数对幅频曲线及其不稳态区域的影响Fig.9 Effects of fractional-order coefficient K1 on the amplitude-frequency curves and their unstable regions

当分数阶阶次p分别选取0.1，0.5和0.9 时，周期解的振幅曲线和稳定区域判别曲线如图10所示。随着分数阶阶次p的增大，系统的非线性特性略有减弱，并由式(14)可知，系统的等效阻尼逐渐增大，因此导致系统共振振幅逐渐减小，同时等效刚度随着p的增大而减小，引起系统共振频率也逐渐减小。另一方面，随着分数阶阶次p的增大，系统不稳定区域也在逐渐减小。因此，分数阶系数K1和阶次p对系统的共振振幅、共振频率以及不稳定区域均有影响。

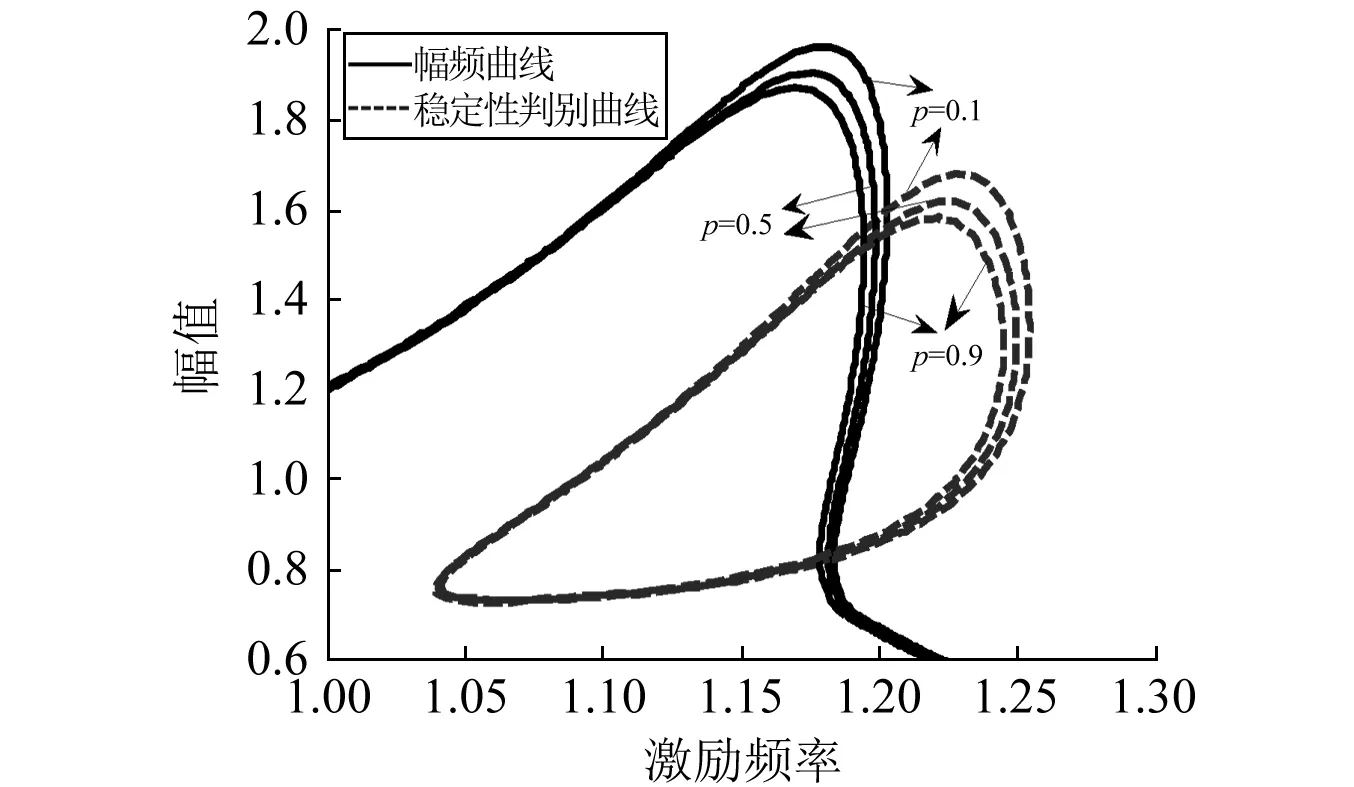
注：m=10;c1=1;c2=0.5;F=3;k1=10;k2=7;δ=0.7; K1=0.1;p=0.1,0.5,0.9图10 分数阶阶次幅频曲线及其不稳态区域的影响Fig.10 Effects of the fractional-order order p on the amplitude-frequency curves and their unstable regions

最后分析分段间隙对系统振动特性的影响。保持其它参数不变，分段间隙分别取δ=0.3，0.6和0.9时系统的幅频曲线及其相应的不稳定区域如图11所示。随着分段间隙的增大，系统的不稳定区域位置变化明显，δ=0.3时对应的幅频曲线和稳定判别曲线没有交点，周期解是稳定的。随着δ的加大，不稳定区域逐渐加大，周期解也出现不稳定性区域，并随之扩大。另一方面，系统共振区域的频带变窄，共振频率逐渐变小，共振振幅随着分段间隙的增大明显加大，但是当间隙过大，超过系统的共振峰值时，系统的非线性区域会消失，呈现出完全的线性特性。

注：m=10;c1=1;c2=1;F=3;k1=10;k2=7; δ=0.3,0.6,0.9;K1=0.1;p=0.5图11 分段间隙对幅频曲线及其不稳态区域的影响Fig.11 Effects of the clearance δ on the amplitude-frequency curves and their unstable regions

5 奇异性分析

为了更全面地了解分数阶分段系统主共振的频响特性，以下应用奇异性理论分析主共振的分岔，找出系统参数变化对该分数阶分段系统响应特性的影响规律。把幅频响应方程在δ点进行泰勒展开，略去高次项后可以得到

b4a4+b3a3+b2a2+b1a+b0=0

(23)

其中，

b3=-2a0c2π(2+π)(c1+c2+(c1+c2-m)ω2+

y4+d2y2+d1y+μ=0

(24)

其中,

y4+d2y2+d1y+μ=0是范式y4+μ=0的普适开折，有两个开折参数d1和d2，根据奇异性理论，以下对此普适开折的持久性进行分析。

分岔点集：B=Φ;

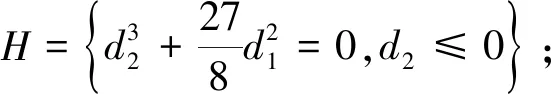
双极限点集：D=Φ；

系统的转迁集为：∑=B∪H∪D

系统的转迁集及分岔图如图12所示。可以看出，转迁集把二维开折参数d1,d2组成的左半平面(由于d2≤0)分成了两个区域Ⅰ,Ⅱ，每个区域内系统的分岔是持久的，在分界线上，系统的分岔是不持久的。两个区域内分别得到了如图所示的Ⅰ1,Ⅰ2,Ⅰ3,Ⅱ1和Ⅱ2五种不同的分岔曲线，系统在不同区域的分岔曲线代表了系统在这些区域产生的不同的动力学行为，可以看出，在同一区域内得到的分岔图都是拓扑等价的，不同区域得到的分岔图是拓扑不等价的。系统呈现出的不同的分岔行为代表了系统在不同的参数作用下的动力学行为，通过改变系统的参数，可以改变系统的动力学行为，这可为合理选择系统参数提供理论参考。