航空发动机附件齿轮行波共振噪声测量与分析
2019-12-02何刘海吴桂娇武昌耀
何刘海, 吴桂娇, 王 平, 武昌耀
(中国航发湖南动力机械研究所 中国航空发动机集团航空发动机振动技术重点实验室,湖南 株洲 412002)
中小航空发动机的附件从动锥齿轮故障率较高, 齿轮辐板裂纹故障占大部分,且都为高周疲劳产生裂纹,因此需要了解齿轮的共振频率和共振转速,避免出现重大故障事件。中小航空发动机转速高,附件齿轮齿数较多,导致其啮合频率较高,甚至超过了20kHz,且中央锥齿轮副啮合能量较大,容易激励齿轮的高阶模态。所以对附件齿轮行波共振进行测量与分析具有重要的理论和工程应用价值。
在目前的试验中,齿轮行波共振频率的获取主要是通过测量加速度信号和动应力信号。加速度传感器通常安装在附件传动机匣合适的位置测量齿轮副和轴系的振动信号[1-6],通过信号处理技术如小波降噪、阶次跟踪等分析齿轮的振动特性,得到齿轮的行波共振频率。这种测量方法虽然能反映部分的齿轮振动信息,但其主要有两大缺点:其一,一般加速度传感器的频响范围为1~10 kHz,齿轮的行波共振频率远远超出了加速度传感器的线性频响范围;其二,加速度传感器安装在附件机匣靠近齿轮的位置,考虑到传递路径和噪声信号的影响,其信号信噪比低,导致分析结果误差较大。航空发动机附件齿轮辐板动应力测量方法也可以通过阶次跟踪分析出行波共振转速[7],但其成本高,试验周期长,存在高速旋转情况下,离心力会使应变片容易损坏,以及滑环引电器使用寿命有限等问题。
为了解决上述缺点,准确测量某航空发动机从动锥齿轮行波共振频率和转速,本文提出了一种新的测量方法,该方法通过声波导管测量齿轮箱内部齿轮副振动产生的机械噪声信号,采用时频分析技术分析噪声信号得到齿轮的行波共振转速和频率,并与通过有限元方法计算获得的齿轮行波共振转速作比较。最后,改变齿轮啮合的边界条件,分析齿轮各阶行波频率、幅值的变化,为优化设计、装配提供参考。
1 行波共振理论
锥齿轮形状和轮盘相似,很容易发生节径型振动。根据薄板弯曲振动理论,在极坐标中,盘上某点的横向位移为x,可用极坐标r,θ及时间t来描述[8-9]。设位移为
x(r,θ,t)=R(r) cosmθcospt
(1)
式中:R(r)为沿径向变化的幅值;m为节径数;p为自振角频率。
由于振动时,节线上的位移为零,代入式(1)可得

可见,节线与时间无关,节线在齿轮辐板上的位置是不变的,称为驻波。由三角函数的关系,式(1)可以写成
(2)
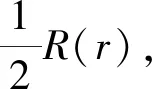
cos (mθ∓pt)=0
(3)
由此可得余弦波节线相对于盘的角速度为
东亭的人们为这事感慨数日。迎宾大道说来也算是武汉最漂亮的马路,修了几轮,成了现在花团锦簇的样子。车来车往,从不堵车。罗爹爹每天晨练要从迎宾大道过,经常夸说:“一走到这条路上,心里硬像是喝汤一样舒服。”
(4)
可见,这两个余弦波的节线(波形)以大小相等,方向相反的角速度在盘上旋转,称为动波。以上讨论盘是不动的,即ω=0,当盘以角速度ω旋转时,则行波相对于地面移动的角速度ω1,ω2为
(5)
(6)
此时的自振频率p高于不转情况的自振频率。式中以角速度ω1旋转的行波,其旋转方向和盘旋转方向一致,成为前行波;式中以角速度ω2旋转的行波,其旋转方向和盘旋转方向相反,成为后行波。盘相对于地面振动的角频率Ω1(或Ω2)应是ω1(或ω2)的m倍,即
Ω1=mω1=p+mω
(7)
Ω2=mω2=p-mω
(8)
或者
(9)
式中:ft为行波频率(“+”对应于前行波,“-” 对应于后行波);fs为固有频率;n为转速,r/min;m为节径数。
采用静止坐标系时,齿轮的节径型振动是前、后行波节径型振动,其固有频率随转速变化。当前、后行波固有频率和激振频率相等,且激励力方向和节径振动方向一致时,就会发生行波共振。采用与齿轮同转速同向旋转的动坐标时,齿轮节径型振动是驻波,齿轮的固有频率简称动频。
2 声波导管原理
在声学测量技术领域里常常要用到声波导管,均匀截面声波导管的主要优点之一在于[10-11]:当声波频率低于管的截止频率时,能够获得良好的没有衰减的平面声波。管中平面波的获得原理如下[12-13]:
设半径为a的圆柱形管,一端无限延伸,管的径向坐标为r,极角为θ,管轴用Z表示,则圆柱形管的声波声压p的三维波动方程为
(10)
在刚性管壁的条件下,按照m阶柱贝塞尔函数方程及其递推关系,可求得管中声压解为
pmn=Amncos(mθ-φm)Jm(Kmnr)ej(ωt-kzz)
(11)
当m=0,n=0时
p00=A00ej(wt-kz)
(12)
p00即为沿Z轴直线传播的(0,0)次平面波,其余称为(m,n)次高次波。可以确定圆柱形管中声波导管的截止频率为
(13)
基于声波导管的附件齿轮噪声测量技术主要是基于管道声学原理,将复杂环境下的机械噪声通过专门设计的声波导管传递出来,采用与管道壁齐平安装或垂直安装的普通传声器进行测量,获得机械噪声的平面波。
3 齿轮振动特性计算
本文的研究对象为从动锥齿轮,三维模型如图1所示,其齿数为43齿。齿轮材料为12Cr2Ni4A,材料性能参数列于表1,工作时齿轮最高工作温度为150 ℃,工作转速为34 000~45 000 r/min。

表1 材料性能参数Tab.1 Material performance parameters
参考文献[14-15],采用十节点四面体单元对锥齿轮进行网格划分,共有416 266个单元,619 297个节点,有限元网格见图1。通过A,B两个轴承安装处的中间平面上一圈节点与各自中心轴线上的一个节点建立RBE2多点约束单元及中心节点创建接地弹簧模拟两个轴承支撑面,弹簧的刚度系数即为轴承刚度系数,见表2。并且约束内花键处节点的周向位移。本次计算考虑的激振源为从动锥齿轮转频和齿轮副啮合力。

图1 从动锥齿轮模型及有限元网格Fig.1 Model and finite element mesh of the bevel gear

轴承名称刚度/(N·m-1)轴向径向双内圈双列角接触球轴承5.20×1071.38×108
本文只给出从动锥齿轮在航空发动机最大转速范围内的节径型振动,计算得到的模态(动频)振型如图2所示。当采用静止坐标系时,齿轮的节径型振动是前、后行波节径型振动,其振型一样,振型节线相对于齿轮辐板旋转,从动锥齿轮行波共振振型、转速及共振频率的计算结果见表3。因计算的共振转速为发动机燃发转子转速Ng,故以主动锥齿轮转频(发动机转子转频)为基频,则齿轮副啮合频率为38倍基频(主动锥齿轮38齿),即K=38,从动锥齿轮转频与基频的倍数关系为K=38/43=0.884。
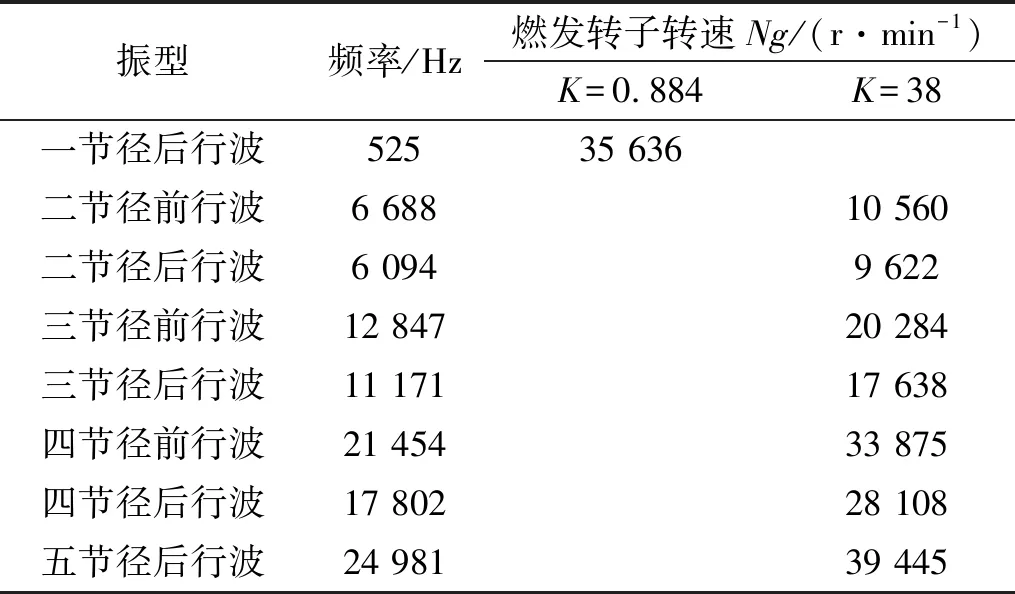
表3 齿轮共振转速Tab.3 Gear resonance speed
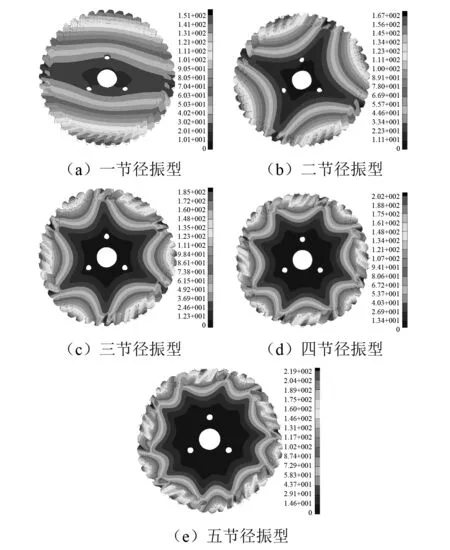
图2 齿轮节径振型Fig.2 Mode shapes of gear
4 测量方法及分析
4.1 测量方法
在齿轮啮合过程中,齿轮的时变刚度、传动误差以及齿面摩擦等会引起齿轮的啮合冲击力,啮合冲击力激起齿轮振动并产生振动传播,从而导致声辐射。由于齿轮副啮合是在附件传动机匣内部,根据声音传播的特性,声音在附件传动机匣里将发生反射、折射、透射,因为附件传动机匣内齿轮多,振动声源丰富,且声学边界条件比较复杂,将会形成比较复杂的声场,如果直接在附件传动机匣外面测量声信号,不仅信号失真,且背景噪声比较大,获取的信号信噪比低。
声测法的试验原理为:在附件传动机匣靠近从动锥齿轮辐板处设计一个声波导管,使得声波导管一端靠近并垂直于从动锥齿轮辐板边缘,另一端伸出机匣外。由于圆形管道的截止频率与管道半径成反比[16],故设计导管半径较小,使得管道的截止频率较高,从而简化了声场,提高了信噪比。参考齿轮共振转速的计算结果,本文采用的声波导管半径为8 mm,按式(13)算得平面波截止频率为24.9 kHz,满足试验使用要求。把声传感器垂直于导管管道壁进行安装,通过声波导管直接测量齿轮机械声信号。试验结构原理图如图3所示。
声信号测试分析系统包括声传感器、采集卡以及相配套的软件分析系统。试验器为某附件传动试验器,主要包括:起动电机、滑油箱、滑油泵、增速箱、联轴器、某航空发动机附件传动单元体(试验件)、测试控制系统等。采用此测试设备,获得的齿轮振动声信息用声压和声压级来描述,声压是对一段时间内瞬时声压(存在声波时,某一点上气压和平均气压的瞬时差)取均方根值,单位为Pa;声压级是使用对数标度来度量声压,可以表示声振动能量的大小,单位为db。
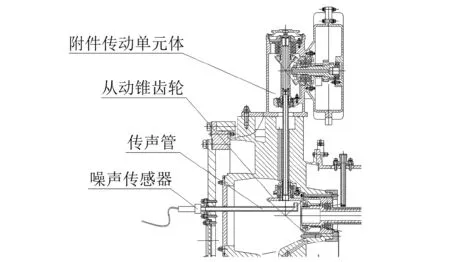
图3 试验原理图Fig.3 Experiment schematic
试验过程为转速扫描试验:试验过程中缓慢推转速,从起动一直推转速到45 000 r/min(主动锥齿轮轴的转速),然后停车。试验分两次进行,两次试验只改变从动锥齿轮的装配状态,其余试验条件不变。第一次从动锥齿轮的装配状态为:按照设计要求进行装配,即锥齿轮组件在装配时,紧固轴承座的4个自锁螺母拧紧力矩为6 N·m,附件锥齿轮副齿隙为正常状态;第二次从动锥齿轮的装配状态为:锥齿轮组件在装配时,紧固轴承座的4个自锁螺母拧紧力矩为1.5 N·m,且附件锥齿轮副齿隙为增大状态,实际测得周向齿隙为0.42 mm。
4.2 试验结果分析
第一次试验的全过程时频云图如图4所示。根据行波共振原理,节径前行波频率随转速升高而增大,节径后行波频率随转速升高而减小,故随转速变化,各节径前、后行波频率线关于各节径动频线对称。结合计算结果,从图中可以明显看出三、四、五节径的前后行波频率线,由于背景噪声(中低频噪声)的影响,一、二节径前后行波不是很明显。从图4可知,各节径行波在试车过程中一直存在,在没有发生行波共振时,声压幅值很小,其原因是齿轮啮合形成的冲击是宽频带激励源,它能够激励起各阶行波,但其冲击能量有限;再加上复杂环境激励(随机信号),其分布到整个频带上能量也小,故行波响应幅值也小。
行波共振的判断依据是:激励(特征)频率线和各行波频率线的交点即为共振点,此时激励频率和前后行波频率相等,振动能量变大,发动机的转速即为共振转速。从图4可知,从动锥齿轮转频线(K=0.884)被低频噪声淹没,故不分析。图4中啮合频率线(K=38)和各阶行波频率线相交的点发生行波共振,此时啮合频率等于各行波频率,声压幅值变大。图4中标记的亮点即为二、三、四、五节径前后行波共振区域。由试验数据分析得到的试验结果见表4。表4中的声音幅值大小采用声压来描述,转速均为主动锥齿轮转轴的转速,即激励源(啮合频率)为38倍频。从表4中可以看出,试验结果和有限元计算的结果比较吻合,最大误差为3.75%,彼此相互验证了准确性。
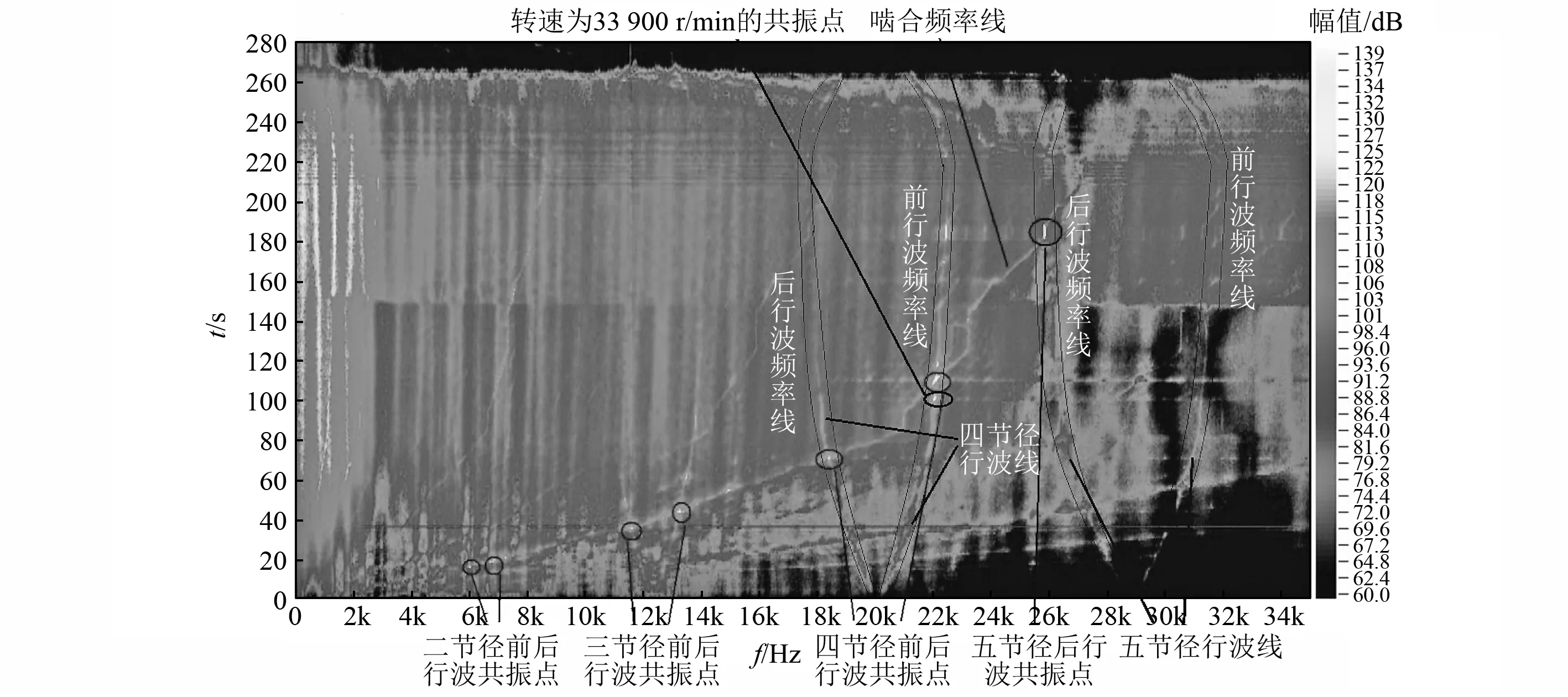
图4 时频云图Fig.4 Time-frequency analysis

表4 声测法测试数据(K=38)Tab.4 Test data based on acoustic signal (excitation source is the meshing frequency)
有限元计算只考虑了行波频率线和激振频率线K=0.884(转频)或K=38(啮合频率)相交的共振点,除此之外,从时频云图中可以看出,四节径前行波频率线在转速为33 900 r/min时出现亮点,即能量变大,此时和行波频率线相交的频率线为啮合频率的边频线(K=39),故可知共振激励源除了啮合频率外,还包括啮合频率调制主动锥齿轮轴转频的边频带,相应的频谱图如图5所示。此时主动齿轮轴的转频为565 Hz,啮合频率为21 485 Hz,而行波共振频率为22 050,相差轴转频,即边频。啮合频率和转频成38.026 5倍数关系,与理论值38倍有误差,其原因是:①分析频带较高,谱线数有限,频率分辨率较低;②试验过程是快速推转速,试验转速不稳,造成测试误差。此时四节径前行波共振声压幅值为87.3 Pa,相对于其他振型声压幅值较大,其原因可能是[17-18]:在这种边界条件下, 四节径前行波模态阻尼比小,同样的激励力产生较大的振动幅值,声压幅值也相应变大。根据时域信号波形以及频谱边带形状,可以看出振动信号产生了幅值调制。齿轮的幅值调制是由于齿面上的载荷波动、齿轮加工误差(如齿距不均)、齿轮偏心以及齿轮故障所产生的局部性缺陷和均布性缺陷等因素引起的。故实际分析中需要考虑这些因素引起齿轮行波共振的可能性。
第一次试验结果与第二次试验结果对比情况见表5。由表中数据可知,改变从动锥齿轮的边界条件,考虑激振频率为K=38的情况下,齿轮的行波共振转速变化不大,其中二节径前行波共振转速变化最大,为3.1%,高阶行波共振转速变化很小,均小于0.6%,最小为0.2%;而共振声压幅值从整体上看第二次要比第一次的结果大一些,其原因是在改变边界条件下,齿隙变大,齿轮副的啮合力增大,即激励能量增大,共振能量相应增大。由于篇幅有限,故第二次试验结果时频云图及频谱图不一一列出。
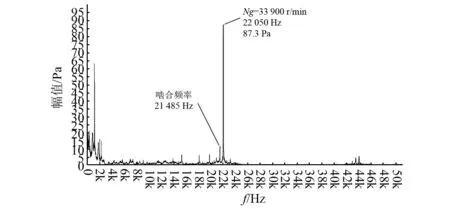
图5 激励源为啮合频率边频带的行波共振频谱Fig.5 Frequency spectrum of travelling wave resonance excited by mesh frequency band

表5 不同边界条件下的行波共振结果对比(K=38)Tab.5 Comparison of traveling wave resonance results under different boundary conditions(K=38)
5 结 论
针对从动锥齿轮行波共振转速测量困难这一问题,本文提出了一种基于声波导管的声学测量方法,该方法采用声波导管获取封闭在机匣内的从动锥齿轮啮合时产生的机械噪声,通过机械噪声信号的分析和处理,得到齿轮行波共振特性。通过理论分析和试验研究,主要结论如下:
(1)对采集的声信号做时频分析,可以根据行波频率线与转频线、啮合频率线的交点获得各节径前后行波的共振转速,并且和有限元理论计算对比,共振转速误差均小于3.75%,可表明:测量方法有效,试验结果准确。
(2)传动过程中存在的齿轮啮合冲击力和复杂环境激励(随机信号),可以激励起各个节径型振动,但能量很小,故时频云图中二、三、四、五节径行波一直存在,没有特征频率线和它们相交时,能量有限,幅值很小。
(3)齿轮行波共振的激励源除了啮合频率之外,还包括啮合频率调制主动轴转频的边频带,它能够激励四节径前行波产生共振,故齿轮存在磨损、偏心等故障时,会出现调制信号,激励源变多,发生行波共振的可能性更大。
(4)在减小轴承座装配力矩和增大齿轮副齿隙条件下,从动锥齿轮行波共振转速变化(特别是高节径行波共振转速)很小,和原始边界条件下相比,最大变化为3.1%,但共振声压幅值变大很多,故需要提高装配要求,避免加大行波共振能量,造成齿轮高周疲劳破坏。
