基于VMD和SVDD的滚动轴承早期微弱故障检测和性能退化评估研究
2019-12-02房立清赵玉龙齐子元
王 斐, 房立清, 赵玉龙, 齐子元
(1.武警士官学校 军械系,杭州 310023; 2.陆军工程大学 石家庄校区火炮工程系,石家庄 050003)
滚动轴承是大型机械系统的重要零部件,一旦轴承失效将会导致整个机械系统的灾难性故障,造成巨大的经济损失和严重事故,目前针对滚动轴承的状态监测和维修策略一直是研究的热点。基于状态的维修CBM(Condition Based Maintenance),或称视情维修,是对机械系统的健康状态进行实时监测,管理和维护,提高整个系统的运行可靠性[1]。轴承从正常运转到完全失效往往要经历一系列不同的性能退化过程,如果能够在轴承运行过程中监测到早期微弱故障及轴承性能退化的规律,跟踪其故障的发展,那么就可以使设备维护计划的制定具有针对性,因此滚动轴承的故障退化程度的评估是开展视情维修的基础和重点[2]。故障退化程度评估要求状态特征要对性能退化程度要有量化反应能力,进而实现对全寿命周期中任意时刻的退化程度进行定量的度量,而非单纯描述不同故障之间的差异;这是故障退化程度评估区别于传统故障诊断的方面。
故障退化程度评估包含两个方面:一是性能退化特征的提取;二是退化特征指标的评估。针对这两方面,国内外学者进行了大量的研究,文献[3]提出了一种基于模糊C均值聚类(Fuzzy C-means Clustering,FCM)的设备性能退化评估方法,以正常状态和失效时刻的数据为基础,建立智能评估模型,在对滚动轴承性能退化评估中取得了良好的效果;文献[4]提出了基于流行学习特征提取和高斯混合模型的退化评估方法,效果优于时域特征提取方法;文献[5]提出了基于隐马尔可夫的多通道融合性能退化评估模型,通过滚动轴承加速寿命数据验证了方法的有效性;文献[6]提出了结合EMD(Empirical Mode Decomposition)分解特征提取和K均值聚类的故障退化评估方法,可以较好的发现早期故障退化阶段;这些方法很好的实现了特征指标的提取与故障程度的评估,但对于早期微弱故障的检测效果并不是很明显。
变分模态分解(Variational Mode Decomposition,VMD)是文献[7]提出的一种非递归的自适应信号分解方法,VMD通过求解变分模态最优解实现模态分解,可将一个非平稳振动信号自适应地分解为若干个不同中心频率的本征模态函数(Intrinsic Mode Function, IMF)之和,具有精度高、收敛速度快、对噪声有较好的鲁棒性等特点,与EMD和EEMD方法相比,有效克服了端点效应与模态混叠现象。目前基于VMD方法的机械故障诊断领域取得了很好的效果[8-13]。
支持向量数据描述(Support Vector Data Description, SVDD)[14]是一种有效的单值(One-class)分类方法,其核心思想是通过非线性映射将样本映射到高维的内积空间,在特征空间中寻找一个包含全部或大部分样本且体积最小的超球体(最优超球体)。近年来,SVDD方法在故障检测、脸部识别、语音识别、图像恢复等领域取得了良好的效果。利用SVDD的单值分类特性,区分正常状态和其他退化状态,可有效实现机械零件性能退化程度的评估[15-18]。
基于上述描述,本文提出了结合VMD分解和SVDD的滚动轴承性能退化评估方法,利用VMD方法对振动信号进行分解,选取对故障较为敏感的模态分量,提取分量的奇异值并结合时域特征、复杂度特征组成滚动轴承综合特征指标;利用SVDD在单值分类问题上的优势,仅使用正常样本的综合特征指标进行SVDD评估模型的构建,通过滚动轴承全寿命数据进行模型的验证,验证结果表明本文所提出的方法不仅能有效的描述滚动轴承在全寿命周期内的性能退化规律,同是对轴承早期微弱故障的发生具有良好的预警能力。
1 变分模态分解原理介绍
VMD算法的核心思想是在变分框架中对信号分解,每个模态分量的频率中心及带宽在迭代求解变分模型的过程中不断更新,最后将信号自适应分解为K个IMF函数。分解过程的数学模型为
(1)
式中:f为输入信号;uk为分解得到的K个IMF分量;ωk为各IMF对应的频率中心。
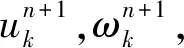
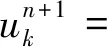
(2)

(3)
VMD方法相比EMD方法,在含噪脉冲信号分解,故障特征频率提取,克服模态混叠方面有很大的优越性。因此,本文将其应用于滚动轴承信号的分解,并进一步提取故障特征作为轴承性能退化评估的特征指标。
2 支持向量数据描述
SVDD可以有效解决单值分类问题,其核心思想是将给定的训练数据映射到高维空间中,在高维空间中寻找一个体积最小的超球体,使得训练数据尽可能多地包含于在该超球体中,不属于该类的数据则位于超球体之外。其数学模型构建如下:
给定一个目标类样本集X={x1,x2,…,xn},定义一个包含所有或几乎所有目标类样本的超球体,超球体球心为a,半径为R。考虑到目标样本中可能存在少数野点,为了提高算法对训练样本中野点的鲁棒性,引入松弛因子ξi,允许部分样本点分布于超球体之外,此时SVDD优化问题描述为
(4)
其中,C>0为指定的惩罚参数,用以调节错分训练样本数(球外样本数)和r的大小。为了解决上述优化问题,构造以下拉格朗日方程
式中:αi,γi为拉格朗日乘子。对R,a,ξi求偏导数,令其为0,得到
(6)
将式(6)代入式(2)中得到优化函数
(7)
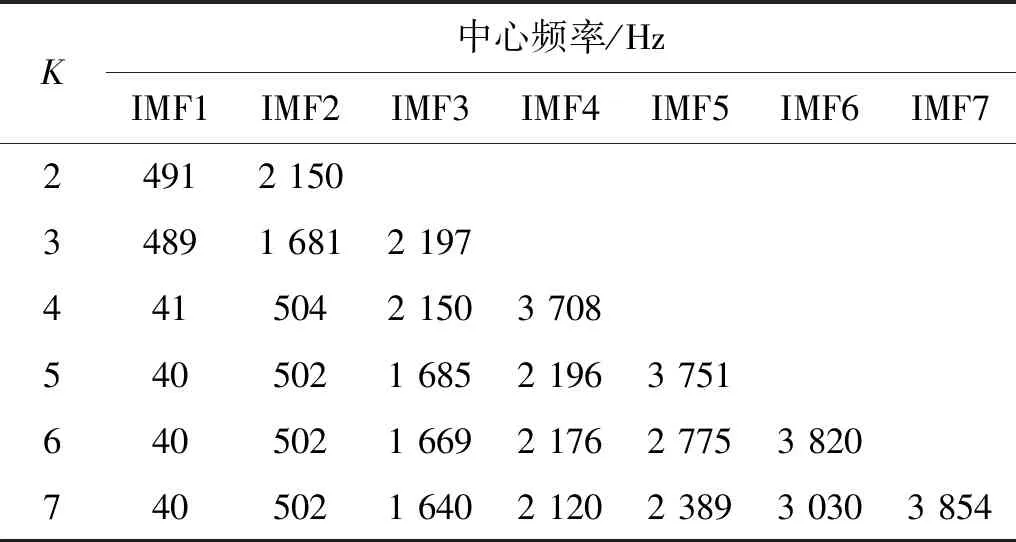
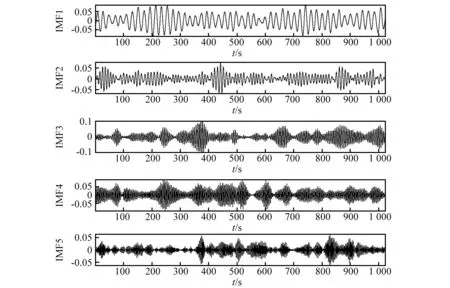
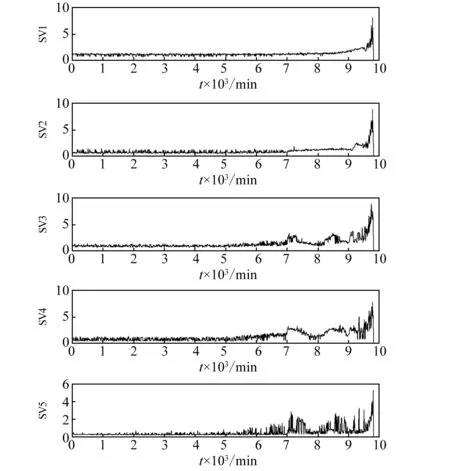
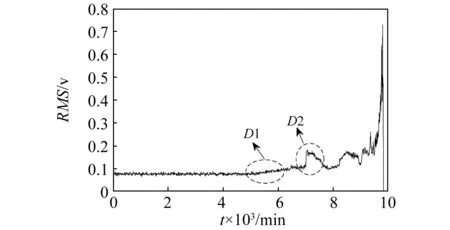
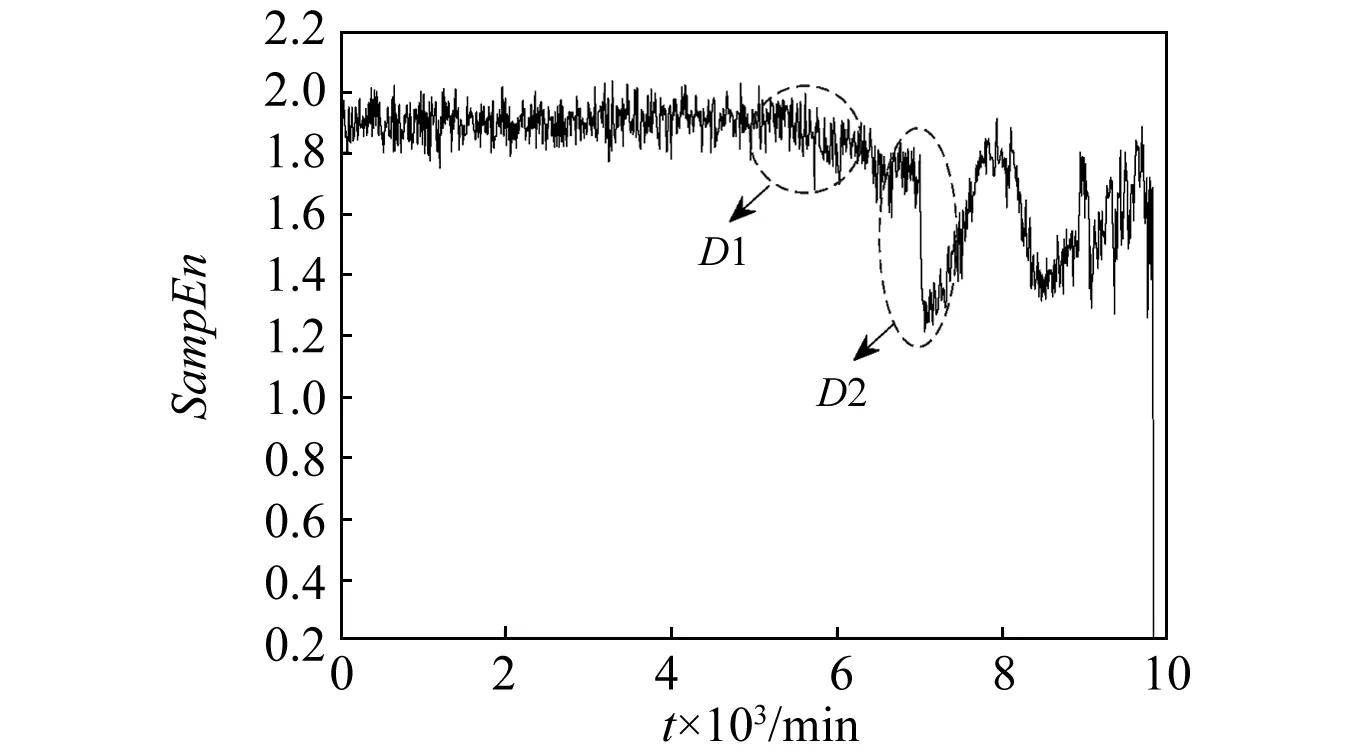
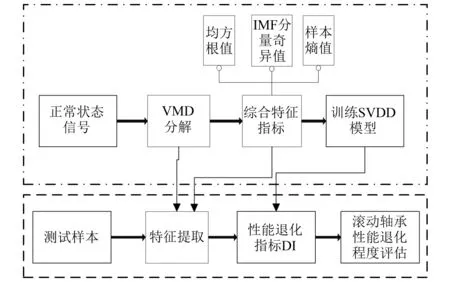
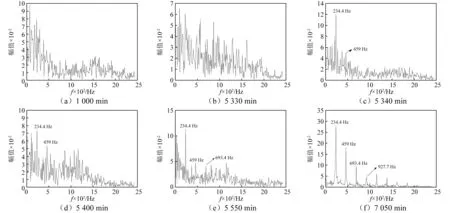
当样本点位于超球体内是,αi=0当样本点位于超球体的边界上,则0<αi R2=‖φ(xsv)-φ(a)‖2=K(xsv,xsv)- (8) 对于新样本z,它与球心的距离可表示为 d=‖φ(z)-φ(a)‖=K(z,z)- (9) 核函数K的使用完成由原空间向高维空间的转换,把原来线性不可分的问题转换成高维空间中线性可分的问题,同是并没有增加太多的计算量。 在轴承退化性能评估过程中,将提取到的正常状态下的样本特征向量作为训练样本输入SVDD进行训练,得到包含正常状态样本的超球体,球心为O,半径为R;新样本与超球体球心的广义距离d可由式(9)求出,当d≤R时,则样本为正常样本;当d>R样本属于故障样本,故障样本d的取值越大则故障程度越深。 本文所使用的滚动轴承全寿命数据来自于辛辛那提智能维护中心轴承疲劳寿命试验台,如图1所示。轴承振动信号每隔10 min采集一次,采样频率20 kHz,采样时间1 s,试验台运行163 h后轴承2外圈出现严重剥落故障,寿命终止,共采集到984组样本,此数据即为轴承的全寿命周期试验数据,经计算轴承2外圈故障频率约为234 Hz,文中采用每组样本的第一列数据进行性能退化评估研究。 图1 轴承疲劳寿命试验台Fig.1 Rolling bearing fatigue life test platform 滚动轴承全寿命周期一般分为正常状态,轻微退化阶段,严重退化阶段和失效阶段,一般寿命评估研究的重点为轻微退化阶段和严重退化阶段。良好的性能退化特征指标一是要在全寿命周期的各个退化阶段要保持相对稳定,另一方面需要在初始退化阶段有较强的敏感性。目前,有多种特征指标被应用于性能退化指标的提取,如时域特征指标(均方根值,峰—峰值,裕度,峭度等),复杂度指标(关联维数、近似熵、样本熵、模糊熵、谱熵等)。本文经过大量分析研究表明,VMD奇异值,均方根值,样本熵值可以更好的反映滚动轴承全寿命周期指标的变化趋势。 3.2.1 VMD奇异值指标 在进行VMD分解之前,需要确定分解层数K的取值,以避免出现过分解可能带来的模态混叠现象。分解层数的选取通过比较各IMF分量的中心频率的方法确定,VMD 分解得到的K个 IMF 分量的中心频率是从小到大依次排列的,随着K的增大,各个分量的中心频率之间的差值会减小,最终出现过分解现象,通过比较各IMF中心频率的差值,来判断是否过分解,进而便可以确定模态个数K。这里以1 000 min时的振动信号为例进行分析,表1为不同模态个数下的中心频率的值,从中可知,当K=7时,分解得到的IMF4和IMF5分量的中心频率相差较小,因此,当K≥7时,信号有过分解的风险,而当模态个数过小时,各模态分量之间中心频率的差值过大,又不足以表征原信号所包含的不同频率成分;考虑到降低特征提取维数的目的,因此最终选取K=5作为VMD分解的模态个数。其它时刻模态个数的选取方法相同,这里不做过多说明。 表1 不同模态个数下IMF分量的中心频率Tab.1 Center frequency of the IMF under different K 将滚动轴承振动信号进行VMD分解,得到5个IMF分量,结果如图2所示,进一步计算每个分量的奇异值,奇异值可依据下面的奇异值分解公式进行求解 A=UQVT (10) 式中:A∈Rm×n为待分解的矩阵;U∈Rm×m和V∈Rn×n为正交矩阵;Q∈Rm×n为对角矩阵。 (11) 式中:0为零矩阵;q=min(m,n);且α1≥α2≥…≥αq>0,αi(i=1,2,…,q)为矩阵A的奇异值。由于IMF分量为一维时域信号,因此每个IMF分量经奇异值分解后得到一个奇异值。经计算得到5个分量在全寿命周期内奇异值的变化情况,如图3所示;图3反映出这5个IMF分量的奇异值在全寿命周期内变化趋势基本一致,但IMF3~IMF5分量的奇异值在故障早期阶段相比IMF1和IMF2变化更为敏感,其包含了更多故障信息,更能表征全寿命特征指标的变化,因此选取IMF3~IMF5奇异值作为部分故障特征向量。 图2 轴承振动信号VMD分解Fig.2 Bearing vibration signal VMD decomposition 图3 IMF信号奇异值在全寿命周期内的变化值Fig.3 The variation of singular value of IMF signal in the whole life period 3.2.2均方根值指标与样本熵值指标 图4 均方根值特征Fig.4 RMS feature 样本熵是常用复杂度特征指标之一,是近似熵的一种改进形式,它通过衡量时间序列复杂性度量信号中产生新模式的概率大小。熵值越大时间序列复杂度越大。样本熵克服了数据偏差,具有较强的抗噪能力和优异的一致性,采用较少的数据段即可得到稳定的熵值。对样本熵的具体计算过程可参考文献[19]。滚动轴承全寿命周期内样本熵值的变化情况如图5所示。 分析奇异值,均方根值和样本熵指标的变化情况,奇异值和均方根值指标在各个不同阶段数值较为稳定,对轻微退化阶段D1和严重退化阶段D2都具有较好的表征能力,样本熵指标虽然在数值稳定性上不如均方根值,但在D1,D2阶段当中值的变化更大一些,对故障状态的变化更为敏感。因此,经综合考虑将这三种指标结合起来作为滚动轴承性能退化综合特征指标,记为V=[SV3,SV4,SV5,RMS,SampEn]。 图5 样本熵特征Fig.5 Sample entropy feature 通过上述分析,本文提出了基于VMD分解和SVDD的滚动轴承性能退化评估模型,如图6所示。其具体步骤为: 步骤1特征提取。对信号进行5层VMD分解,提取IMF3~IMF5分量的奇异值,与信号均方根值和样本熵值组成特征向量V作为轴承综合特征指标。 步骤2利用正常样本信号的综合特征指标作为训练样本构建SVDD分类器,得到包含正常样本超球面O,并得到超球体半径R。 步骤3计算测试样本综合特征指标Vtest,输入SVDD分类器中求得Vtest与超球体球心之间的距离d,并计算得到性能退化指标(Degradation Indicator,DI),以DI值作为性能退化评估的依据 (12) 图6 性能退化评估模型Fig.6 Performance degradation assessment model 从图3~图5可知,滚动轴承在0~4 000 min运行期间内,各特征值保持稳定,可认为期间轴承处于正常工作状态,本文选取运行时间在1 000~3 000 min的200组振动信号作为样本数据用于SVDD的训练样本。其中,惩罚参数C取值为1, 核函数参数σ=90。将滚动轴承全寿命周期的984组数据作为测试样本输入退化评估模型最终得到全寿命周期的DI值,以此作为全寿命周期的评估结果,如图7(a)所示,图7(b)为500~700组样本的DI变化情况,图7(c)为只采用样本熵与均方根值作为特征指标的评估结果,与文中所提特征提取方法相比,监测到初始故障发生的时间晚了约260 min,这说明本文提出的SV3,SV4,SV5特征指标能很好的反映轴承运行状态信息。 图7 基于SVDD的滚动轴承性能退化评估结果Fig.7 Performance degradation assessment results by SVDD 图7(a)和图7(b)中,在运行的0~5 340 min期间样本的DI=0,此阶段的滚动轴承处于正常工作状态,在5 340 min样本的DI>0,说明此时开始出现极其轻微的早期故障,从5 550 min开始故障开始逐渐加深,直到7 050 minDI值急剧变化,说明滚动轴承性能退化加深,故障程度较为严重,之后DI值时而增大时而减小,规律性较弱,从9 100 min开始DI值大幅增大,轴承失效。从对评估结果的分析可以得到以下推论:①5 340~5 540 min,轴承出现极其微弱的早期故障,几乎难以发现;②在5 500~7 040 min,故障程度呈逐渐加深态势;③7 050~9 840 min,DI变化情况复杂,无明显规律,可以认为从7 050 min以后轴承已经处于严重故障状态。 为了验证本文的推论,分别对1 000 min,5 330 min,5 340 min,5 400 min,5 550 min,7 050 min的振动信号作VMD分解,模态个数K=5,取IMF3~IMF5分量重构信号,并对重构信号做包络谱分析,如图8所示。5 340 min时的包络谱分析可以明显检测到234.4 Hz的频率成分,非常接近外圈故障特征频率的理论计算结果234 Hz,5 340 min时刻之前的5 330 min及1 000 min时的正常状态则没有此频率成分,可以认为5 340 min第一次发生了外圈故障;此时的包络谱还存在很多其他频率成分,说明此时的外圈故障非常微弱,5 340 min之后的5 440 min还能较为明显的观察到234.4 Hz及其倍频成分459 Hz,但频率的幅值较5 340 min时更小,这是因为出现微弱故障后故障点被“磨平”使得故障程度减弱,相比5 340 min,5 340~5 550 min的故障更弱,更加难以检测,可以认为5 340~5 550 min滚动轴承处于早期微弱故障缓慢退化阶段;从5 550 min开始,外圈故障特征频率及其倍频成分愈发明显,直到7 050 min时包络谱中几乎只存在故障特征频率及其倍频成分。由此可认为5 550~7 050 min轴承处于性能加速退化阶段;7 050 min以后外圈故障更为明显,本文认为7 050 min以后轴承其实已经处于性能严重退化状态。与文献[20]的评估结果相比,本文方法所检测到的初始故障退化阶段提前了约1 690 min,相比文献[21]提前了约690 min,这充分说明本文所提出的退化评估模型对滚动轴承性能退化有较强的敏感性,而尽早检测到滚动轴承故障情况的发生对机械系统的视情维修又具有重要意义。 图8 不同时间的振动信号包络谱分析Fig.8 Envelope spectral analysis results under different times 为了进一步说明文中所提方法的优越性,同样利用模糊聚类分析算法进行滚动轴承性能退化评估,使用正常样本和故障样本训练FCM评估模型,依然选取V为综合特征指标,将全寿命的特征指标作为测试样本输入评估模型,将测试样本与正常样本特征的隶属度值作为性能退化指标DI,DI∈[0,1],进而得到滚动轴承全寿命周期的评估结果,结果如图9(a)所示,图9(b)为局部放大情况。由图9可知,FCM评估模型的DI值的趋势与图7变化趋势相似,在0~5 000 min期间内DI值波动较大,且FCM模型在6 100 min左右才出现较为明显的DI值减小趋势,相比本文所提方法晚了约550 min,本文所提方法对数据异常点具有较强的鲁棒性,并且在早期微弱故障监测方面明显优于FCM评估模型。同时,本文所提方法只使用了正常状态下的样本作为训练样本,一方面可以减少计算量,简化评估模型;另一方面可以克服实际工业生产中故障样本较难获取的问题,对于进行机械系统性能监测具有重要意义。 图9 基于FCM的滚动轴承全寿命性能退化评估结果Fig.9 FCM-based evaluation of the life-cycle performance degradation of rolling bearings 本文针对滚动轴承微弱故障特征较难提取问题及性能退化程度监测问题,提出了一种基于VMD分解和SVDD的滚动轴承性能退化评估模型,利用轴承全寿命数据对所提出的评估模型进行了验证,主要结论如下: (1)对振动信号进行VMD分解,通过提取IMF分量的奇异值与信号均方根值、样本熵值组成综合特征指标,可以较好的表征轴承性能退化情况。 (2)以正常状态的样本作为训练样本进行评估模型的构建,所得到性能退化评估结果可以准确检测到轴承早期微弱故障的发生,并可以对轴承性能退化情况进行很好的评估,对实际生产中轴承微弱故障的发生和性能退化评估具有很好的指导意义。3 滚动轴承性能退化程度评估
3.1 滚动轴承全寿命实验数据
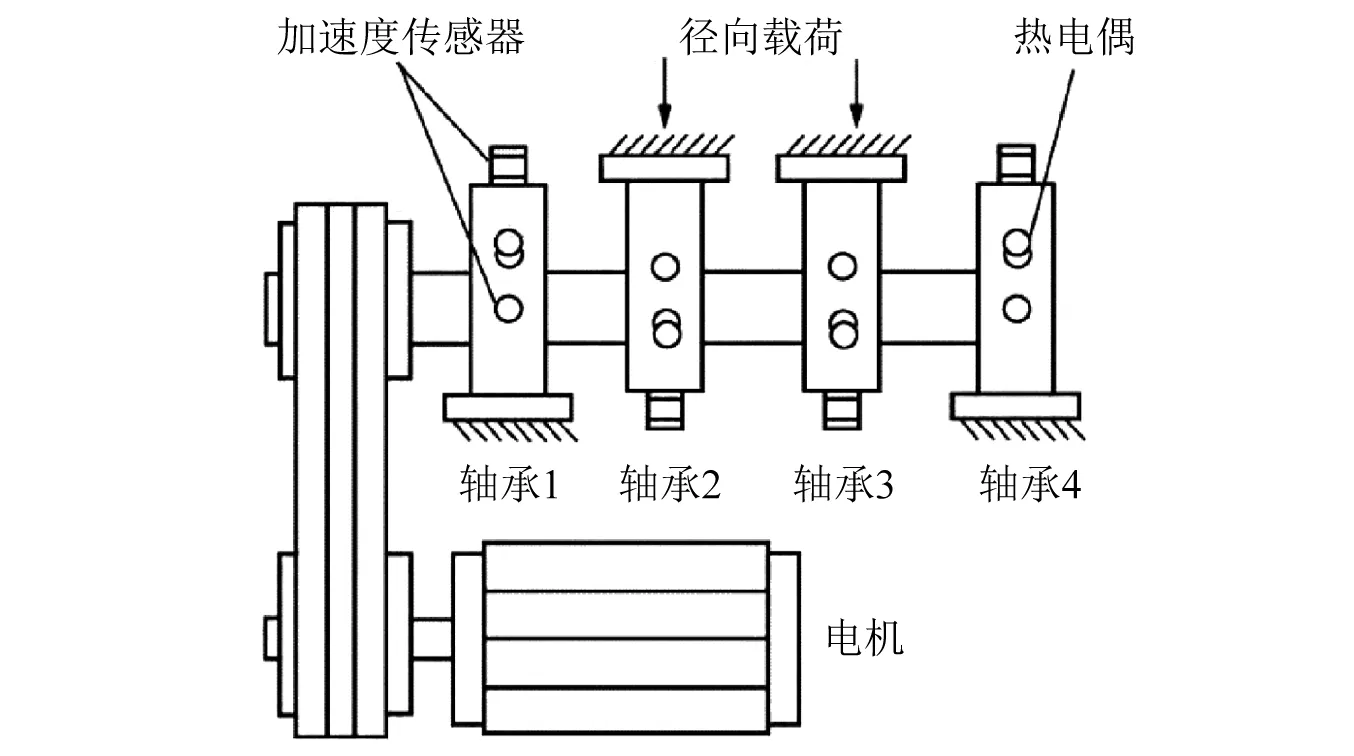
3.2 特征指标的选择
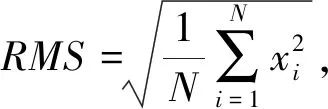
3.3 滚动轴承性能退化评估模型
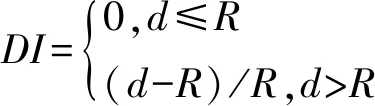
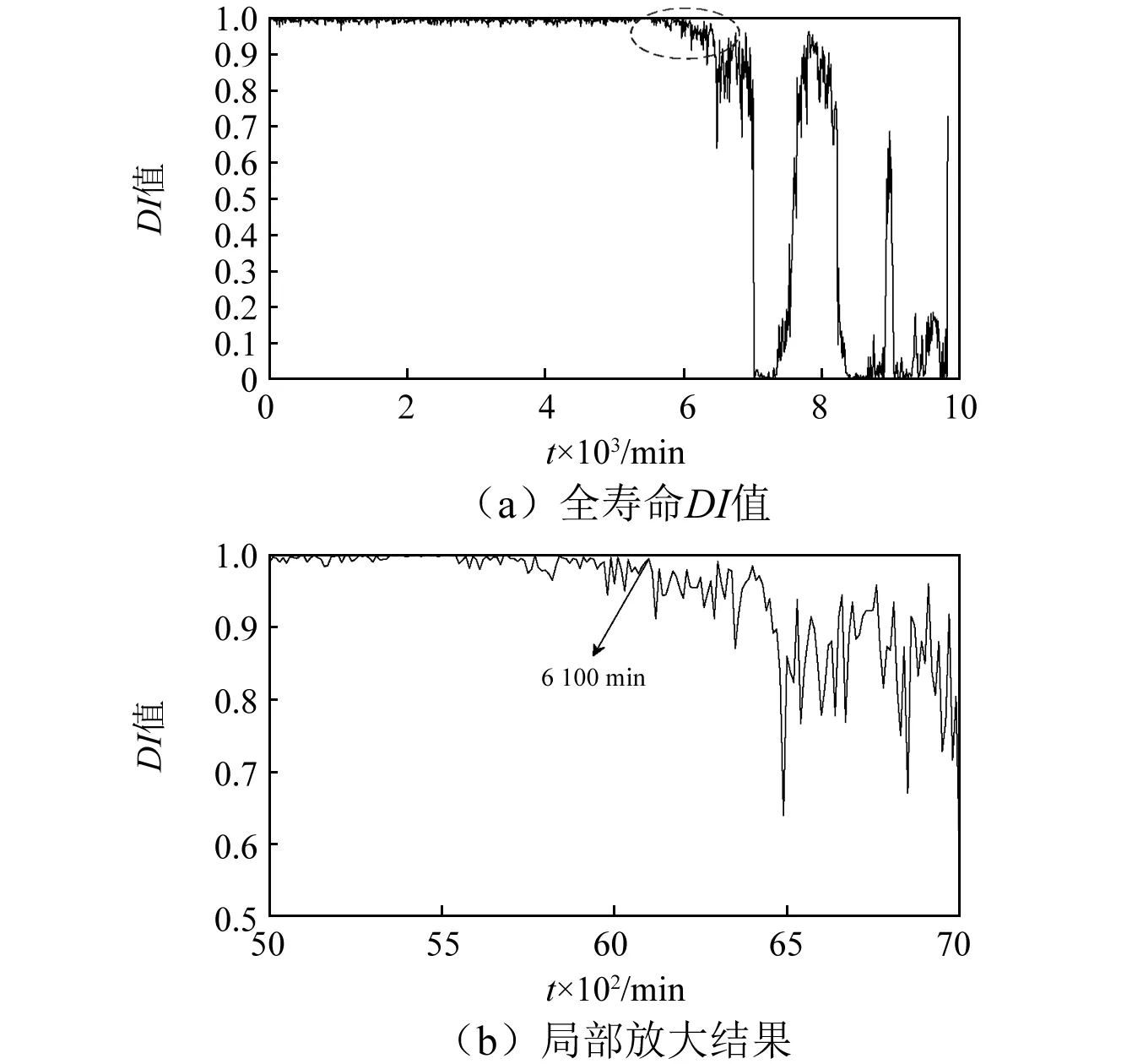
3.4 基于VMD和SVDD的滚动轴承性能退化评估

4 结 论
