Creep relaxation in FGM rotating disc with nonlinear axisymmetric distribution of heterogeneity

Hodais Zharfi

Department of Mechanical Engineering, Esfarayen University of Technology, Esfarayen, Iran

Keywords:Creep FGM materials Rotating disc Nonlinear volume fraction Temperature

A B S T R A C T Rotating discs are the vital part of many types of machineries. Usually there is a tendency to make use of them in higher rotational speeds, but ahead of their complete break down the incidence of vibration, plastic failure or creep relaxation can create serious damages which finally prevent the increase of the rotational speed. The invention of new materials has provided new opportunities to increase the loading capacity and speed of the discs. Functionally graded materials (FGMs) are a kind of new materials utilized in the construction of rotating discs. Consequently an important aspect in the analyses of heterogeneous FGM discs is the study of their creep relaxation. One of the well known constitutive equations for the modeling of creep phenomenon is known as the Sherby's law. Based on the steady state creep, the behavior of a variety of FGM rotating discs are studied. The analysis considers the conditions in which the distribution of volume fraction follows a power-law pattern. The required mathematical model and its solution for the analysis of stress and creep strain rate is represented. Some case studies are considered in which the effects of nonlinearly distributed volume fractions are studied. In the case studies, the analysis of rotating FGM discs made of Aluminum-Silicon Carbide compounds is considered. Besides, the analyses of discs with outside tractions are considered and the effects of typical material compositions upon the creep deformations are studied. For instance, the investigation discloses the significance of the use of FGM hubs in the turbine constructions.

Rotating discs are utilized in various industrial machineries such as the turbines, pumps, automobiles and aircrafts. In most of their applications, discs work at such high rotational speeds and temperatures that generally produce high levels of thermal stresses. For example gas turbine engines rotate at thousands of rpm and some models of air craft turbines are even capable to rotate at speeds beyond 100000 rpm [1]. In these conditions the parallel effects of eccentric inertial forces and high levels of temperature leads to the rise of severe thermo-mechanical stresses and consequently, the increase of creep strains. It is the reason that the study of creep in rotating discs is essential and necessary. Creep can be considered as a failure mode or yet it may be accepted as a constitutional behavior of the material continuum.When creep is characterized as a type of material behavior, one can distinguish different regimes of constitutional behavior usually known as the first, second or third stages of creep [2]. Experimental data shows that most of the creep life passes by in the second stage creep. Therefore usually this kind of creep is more important for the study. In recent years functionally graded materials (FGMs) have attracted particular attention. The reason for this attraction is their recognized merits such as the high strength, light weight, suitable conductivity and good efficiency in high temperatures as well as the resistance against the corrosion. So their utilization in various branches of industry is increased quickly. Usually these heterogeneous materials are made of a composition of two different constituents such as the metal and ceramic parts. In a macroscopic viewpoint, any point of this texture is occupied by a unique material with physical and mechanical properties between the properties of its constituents. In order to perform any mechanical analysis the relevant properties of the harmonized mixture have to be estimated.Based on the researchers endeavor, different rules have been formulated to develop these estimations. According to most of these mixture rules, at any point of a heterogeneous compound,different thermo-mechanical properties of the mixture are functions of the volume fraction of its constituents [3]. In this case if the distribution of volume fraction is provided, the distribution of any material property can be obtained.

Because of the wide spread applications of FGM structures in the severe thermo-mechanical conditions and the subjectivity of creep phenomenon in these conditions, extensive researches have been conducted to study the influence of creep on the deformation of FGM rotating discs. Some of them are mentioned in the following. Nearly the first researches in the creep of rotating discs date back to the works published by Whal et al. [4]. Assuming a power law pattern for the distribution of in-homogeneity and using both the von-Misses and Tresca's yield criteria they have obtained the creep behavior of a rotating disc. Afterwards,these investigations continued by Ma et al. [5]. In their researches they make effort to find the stresses and creeping strains of the gas turbine and jet engine discs using the maximum shear theory. They employed the variable thickness disc and the exponential and power law creep models in their studies [6, 7].This evolutionary research continued until Bhatnagar and Arya [8] who investigated the creep response of an orthotropic rotating disc. They observed that the tangential stress at any radii and the tangential creep rate at the inner radius decreases by increasing the disc heterogeneity. Bhatnagar et al. [9] extended their studies to the variable thickness discs. They used Norton creep law to find the creep behavior of a rotating disc.Gupta et al. [10] used the Sherby and Norton's creep laws to investigate the steady state creep behavior in FGM rotating discs made of linearly varying of SiC particles in pure aluminum base and in presence of thermal gradients. They used the experimental data published by Whal. et al. [4] to validate their results.Gupta et al. [11] found that a rotating disc with decreasing density and thickness in radial direction shows better creeping strength than a disc with constant density and thickness. Singh [12]investigated the effects of the particle content distributions on the creep response of a FGM disc made of SiC particles in pure aluminum base. He used the Norton power law and von-Misses yield criterion in his analyses. He discovered that the influence of particle size on the radial stresses is negligible but the particle size and the pattern of their distribution can be very effective in the levels of tangential stresses and strains. Additional researches have been done by Singh and Ray [13–15] in all of their studies the effect of particle distribution on the stress, creep strain and deformation has been considered. In 2003, Jahed and Bidabadi [16] used the variable material properties (VMP) method to investigate the primary and secondary creep in the axisymmetric problems such as the discs and pressure vessels. Assuming various distribution patterns of SiC particles and thermal gradients in an ANSYS finite element analysis modeled in 2008,Gupta et al. [17] obtained the steady state creep rate, stresses and strains for a rotating disc. Daghigh et al. carried out the initial thermo-elastic and time dependent creep evolution response of rotating ferritic steel disc (1/2 Cr, 1/2 Mo, 1/4 V) using a long term creep constitutive equation. They used a numerical procedure using the Taylor series and Prandtl-Reuss relations to achieve the history of stresses and creeping rates [18]. Zharfi and Ekhtearei Toussi [19, 20] proposed an analytical formulation to study the steady state creep in thin FGM rotating disc using generalized differential quadrature (GDQ) method. They used a plane stress model and determined the creep responses of FGM rotating disc in various boundary conditions and various temperatures field. Hosseini Kordkheili et al. [21] employed a semi analytical solution to study thermo-elastic creep behavior of the FGM disks in time domain. Thermal and structural properties of the base metal in this investigation are considered as a function of temperature. Their result showed that ignoring the temperature dependency of these parameters resulted in a large amount of error in the creep solution consequences. In recent years these trends of creep analysis have been continued. The analysis of creep relaxation in anisotropic composite discs and in the presence of thermal effects [22], rupture and damage after effects of creep deformations [23], creep study in thick FGM rotating disk with two dimensional GDQ method [24] are among the recent studies performed in the framework of the creep analysis in FGM structures.

In more industrial application the performance of the components in terms of efficiency, service life and power transmission certainly depends on the material, rotational speed and operating conditions. For example in the turbine rotors the possibility of heat transmission from the external surface to the shaft and from it to the bearings caused undesirable effects on its functioning and efficiency. Furthermore in some specific applications such as in aerospace engineering where the components weight and durability in high temperature are important, the components need to be fabricated by using of special materials with distinguished properties to resist along the creep deformation [25]. In all recent works only the linear and parabolic distribution of particles are considered for creep analyzes of FGM rotating discs, but in practice the manufacture of a disc with closely linear or parabolic distribution of particles is not an easy task. So it is important to access a more complete model and versatile solution, capable to comply with the real conditions.

In this paper the creep behavior of FGM discs has been investigated. It is assumed that the discs are made of various distributions of SiC particles in pure aluminum. It needs to emphasize that even though in the modeling stage the general pattern of particle distribution is considered, in the case studies only the linear and forth order power function distribution patterns of SiC particles in the radial direction are analyzed. In all case studies, the amounts of particle content at the inner and outer radii are taken to be some definite values. In addition to the particle distribution, the effect of temperature on the response of the FGM discs is investigated too. Moreover the discs with outside traction are considered and the effect of different material compositions upon the creep deformations is studied.

The procedure used in this section for the analysis of creep relaxation in rotating discs is nearly similar to the techniques developed and used in such works [22, 26]. Nevertheless for the sake of sufficiency they are reiterated here. From now on the Sherby's creep law is used to describe the steady state creeping behavior of the FGM rotating discs. Sherby's law is represented as [26],

in which E is the Young modulus of elasticity and Asis,

Here A is a constant and as dictated by the Sherby's law [27], DL,λ and |b| are the lattice diffusivity, the sub grain size and the size of the Burgers vector, respectively. The effective stress is given by the von-Misses isotropic yield criterion as,

where σrand σθare the radial stress and tangential stress,respectively. Experimental results show that creep parameters M and σ0depend on the particle size, P, particle distribution function, V(r) and the level of prevailing temperature, T. Based on the experimental creep data reported by Pandey et al. in 1992 [28] and using a regression technique, Gupta et al. [22]represented the M and σ0functions as,

in which P is the SiC particle size which is considered to be 1.7 μm. So down to the radial variations of the particle distribution in the FGM disc both M and σ0are functions of radial position.Apart from the mechanical parameters, some of the other physical parameters of material are controlled by the volume fraction. For instance a homogenization formula must be provided for the density of the compound. Here and after we have used a linear mixture rule [29]. That is,

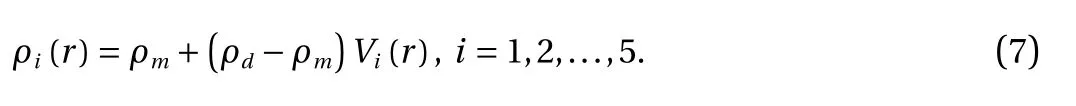
In Eq. (7) the subscript i stands for the disc number. It means that Vi(r) is the volume fraction of the disc enumerated by i.Before starting to develop a closed form solution for the distribution of creep stress and deformation, there are other assumptions that must be asserted. Amongst them are the presumptions of material isotropy and von-Misses yield criterion. Also it is supposed that in comparison with the creep deformations, the elastic deformations are negligible and can be neglected. Compared to other dimensions of the disc its thickness is so small that axial stresses can be ignored and plain stress conditions can be assumed. The creep constitutive equations in a plane stress problem can be expressed as below,

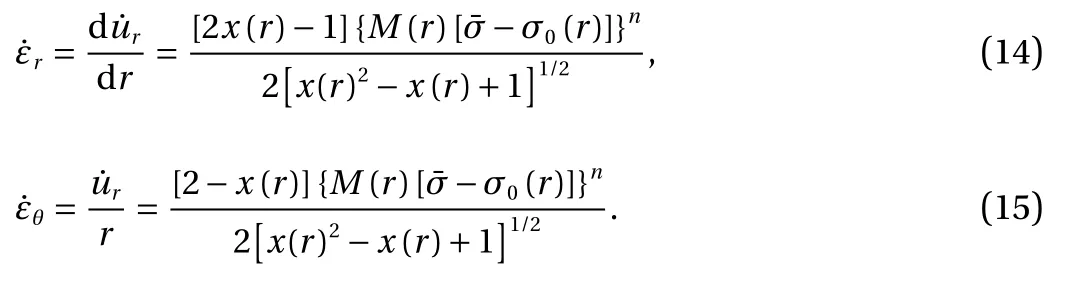
Dividing Eq. (14) by Eq. (15) and integrating the resulted function from the inner radius up to an arbitrary radius r gives,

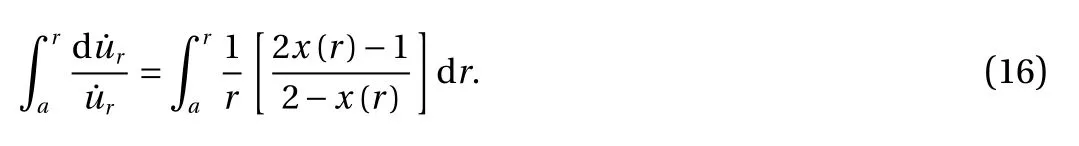
So we have,

where

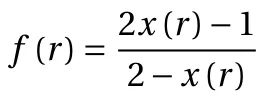
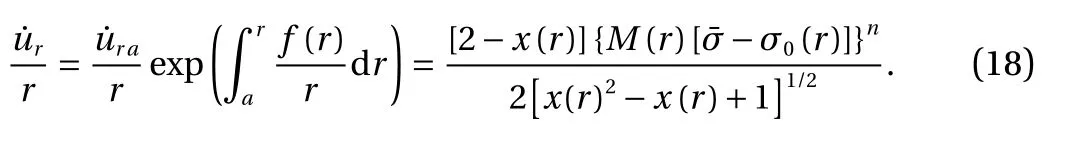
Substituting the effective stress from Eq. (4) into Eq. (18), the tangential stress in each arbitrary radius of the disc is found to be,

In this equation λ1(r) and λ2(r) are,

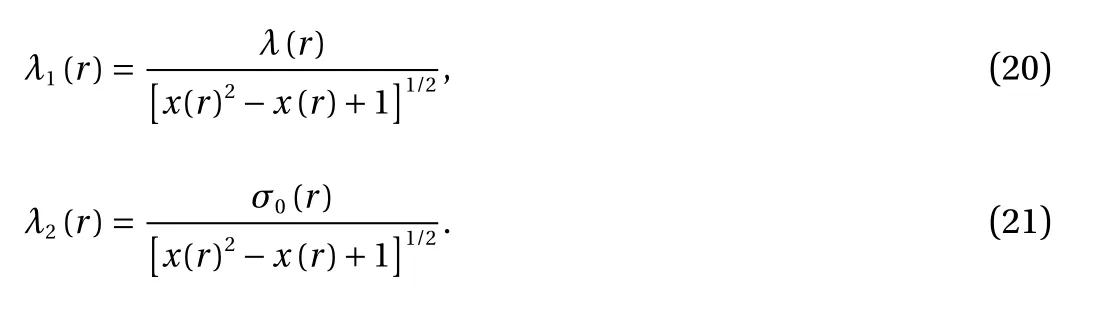
And the parameter λ(r) is found to be,

Now as in Fig. 1, consider a heterogeneous disc rotating with constant angular velocity ω. Applying the equilibrium constraint into an element of the disc, a governing equation is obtained as,

At first it is supposed that disc is rotating under the free-free boundary conditions. It means that radial stresses at the inner and outer radii of the disc are coming to zero. So the boundary conditions of the disc can be written as,

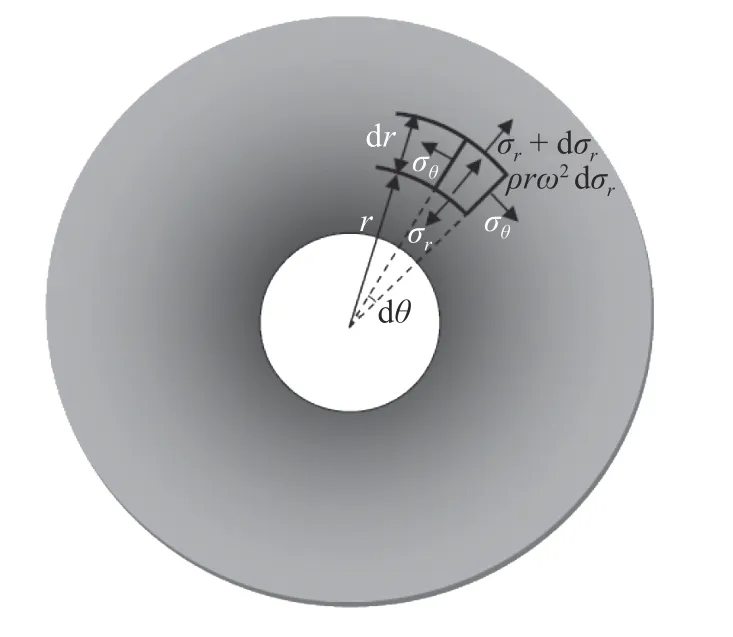
Fig. 1. Schematic image of a heterogeneous disc and a disc element

Using the boundary conditions introduced in Eqs. (24) and(25), and integrating the differential equation in Eq. (23), we get,

Using Eq. (19) and integrating Eq. (26), we can find the radial displacement at the inner radius of the disc. That is,

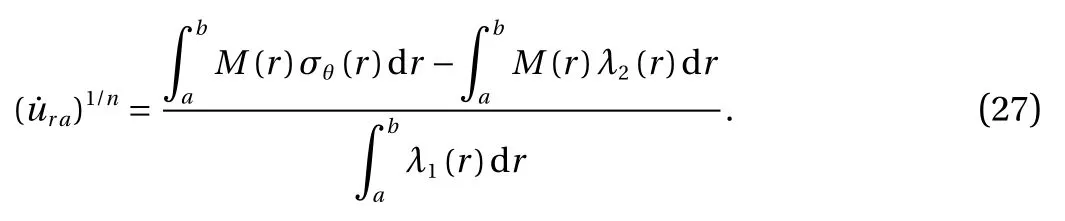
To analyze the creep phenomenon in a rotating disc by the developed formulations, we have to use a proper computational procedure. In our approach at the first step, the average tangential stress is calculated all over the disc. That is,

Using the well-known software of Mathematica the solution is sought. Based on Eqs. (23) and (28) the amount of average tangential stress is obtained. Therefore we have assumed that the tangential stress in each arbitrary radius is equal to this average tangential stress. In other words σθ(r)=(σθ)ave. With this assumption we can find the radial stress in each radius and compute the ratio of radial and tangential stresses indicated by x(r). After computing x(r), the distributions ofλ(r), λ1(r) and λ2(r) are calculated too. Using Eq. (19) and these updated radial function,next approximation is obtained for the σθ(r). Then with the refreshed σθ(r) all above steps are repeated and another new estimation is obtained for σθ(r). This procedure is continued until a suitable convergence is achieved. Finally the values of the radial and tangential stresses, strain rates and displacement rates are obtained. All of these procedures have been studied in cases where volume fraction distribution is nonlinear. The study has been carried out by focusing on five different discs with definite prevailing temperatures. The results have been represented and discussed in the next two sections.

Assume an Al-SiC Particulate composite disc rotating at 1000 rad/s constant angular velocity. The disc profile and dimensions are shown in Fig. 2.

For the sample discs, the distribution of volume fraction keeps to the following pattern.

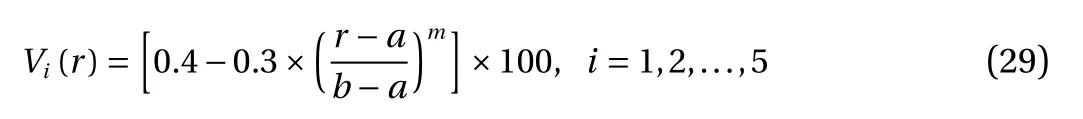
Here five different discs are considered. In disc No. 1, m equalsin disc 2, m isin disc 3, m=1, in disc 4,and in disc 5, m=2. For better comparison in all cases the volume fraction of the inner and outer radii are fixed similarly. Besides in these analyses V1(r) is the radial distribution of volume fraction in disc1. Similarly other indices designate the structure of other discs. Parameter a designates the inner radius of the discs and equals 0.05 m. Parameter b is the outer radius of the discs and equals 0.20 m. Particle distribution in five different discs are shown in Fig. 3.

Assuming a power law creep and similar to Ref. [20] the exponent n in Eq. (1) has been chosen to be 8. Besides in refer to Eq. (7) ρmis the density of the pure aluminum matrix equals 2698.9 kg/m3and ρdi.e. the density of the dispersed SiC phase equals 3210 kg/m3. Accordingly in a various uniform temperatures the distribution of the creep parameters M(r) and σ0(r) in five different sample discs are achieved. Based on the semi-analytical procedure established in the previous section a computer code using Mathematica software was developed to find the radial and tangential creep stresses, strain rates and displacement rates in the FGM discs. Before providing the results of FGM rotating discs, to validate the analysis and the developed computer code, the results of tangential and radial creep strains were computed for a steel rotating disc using Sherby's creep law and compared with the available experimental and theoretical results [4, 10]. Figure 4 shows the comparison result and as it can be seen there is a good agreement between the results.

Fig. 2. Profile and parameters of a typical FGM rotating disc

Fig. 3. Particle distribution in the studied FGM discs

The results of these analyses for different FGM discs and temperatures are represented subsequently. The dimensions of the sample discs and their base parameters are provided in the previous section. The graph of the radial distributions of radial and tangential stresses in different discs at T=650 K is presented in Fig. 5. The figure shows that the difference between the distributions of material heterogeneity can result in the meaningful difference between the stress curves. Besides, the figure shows that a change in the distribution of volume fraction will not alter the radial position of the maximal point of radial stress very seriously. Figure 5 confirms that tangential stresses show off a decreasing trend in the radial direction. Similarly it means that tangential stresses experience a maximum at the inner radii and decreases gradually to reach a minimum at the outer rim. The reason for this type of behavior is the existence of the relatively higher content of particle at the inner radius in comparison with other points in the disc. The results show that the disc with the higher concentration of particle content in the middle side is subjected to less tangential stresses.

To study the effect of temperature on the radial stress, we have selected five different temperatures and investigate their influences upon the stress distributions. Results show that the temperature level has not significant effect on the distribution of the radial and tangential stresses. The effect of temperature on the radial stress and tangential stresses are shown in Fig. 6.

It seems that similar to a statically determinate problem, the stress and material composition decoupling is a result of creep relaxation. This in turn can lead to the independence of temperature and stress fields.

Fig. 4. comparison of theoretical and experimental strains in a rotating steel disc

Fig. 5. Radial and tangential stress in five different discs at T=650 K

The distribution of the radial component of creep strain rate along the disc radius for all five types of the discs is presented in Fig. 7. Results indicate that lower radial creep rates belong to the discs with the higher levels of particle content.

At a temperature of T=650 K all creep rates are compressive.The effect of the temperature on the radial creep rate at disc 1 is shown in Fig. 8. As this figure shows, increasing the temperature leads to the increase of radial creep rates. In discs with low content of volume fraction the rise of temperature results in the critical conditions in which extreme levels of creep rate takes place.The influence of temperature on all five discs shows similar trends but it can be seen that it is more serious for the disc with low particle content.

Also, the results show that the minimum value of radial creep rates occurs at the middle of the discs and its maximum values are at the inner and outer radii. Nevertheless the tangential creep rate displays a different trend. Tangential creep rate is maximal at the inner side of the disc and is minimal at the outer side. It has a monotonic decreasing behavior at the intermediate radii. The radial variations of the tangential creep rates at T=650 K can be seen in Fig. 9. Similar to the radial creep rate, the disc with less particle content has less tangential creep rate and vice versa. The results show that the discs with lower volume content have more severe tangential creep rates at the inner radii. In these analyses all discs are taken to have similar particle content at the inner radii. Even though our further trial (not shown here)reveals that this restriction has no significant effect on the tangential creep rate values.

In order to investigate the effect of the temperature on the tangential creep rates of disc1, as before the tangential creep rates at five different temperatures has been derived. Fig. 10 shows the tangential creep rate variations of Disc1 in different temperatures. As it can be seen temperature has a significant effect on tangential creep rate distributions and with 50 K temperature increasing the value of tangential creep rate reaches to about eight times of its previous value. Figure 9 indicates the tangential creep rate in prevailing temperature of 650 K and a brief comparison between Figs. 9 and 10 shows that the value of tangential creep rate in relatively high temperatures increased about 1000 times.

The variation of radial displacement rate at T=650 K is presented at Fig. 11. Obviously down to the integrated nature of the displacement (compared to the differential nature of strain)this picture does not reveal many of the details appeared in the previous stress or strain curves and predicts a similar behavior for all discs.

Another factor investigated in this analysis is the effect of outlying tractions upon the creeping stress and deformations.Actually in most applications, the high temperature rotating discs are utilized as the hub of a turbine stage in which several blades are attached to its periphery. In such cases the eccentric inertial forces of the blades acts as extra factors to increase the level of disc creeping deformations. To study this phenomenon,assuming a continuous outward traction at the outer rim of the disc, we have,

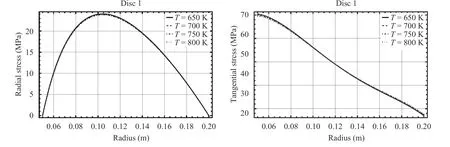
Fig. 6. Effects of temperature on radial and tangential stresses in disc 1

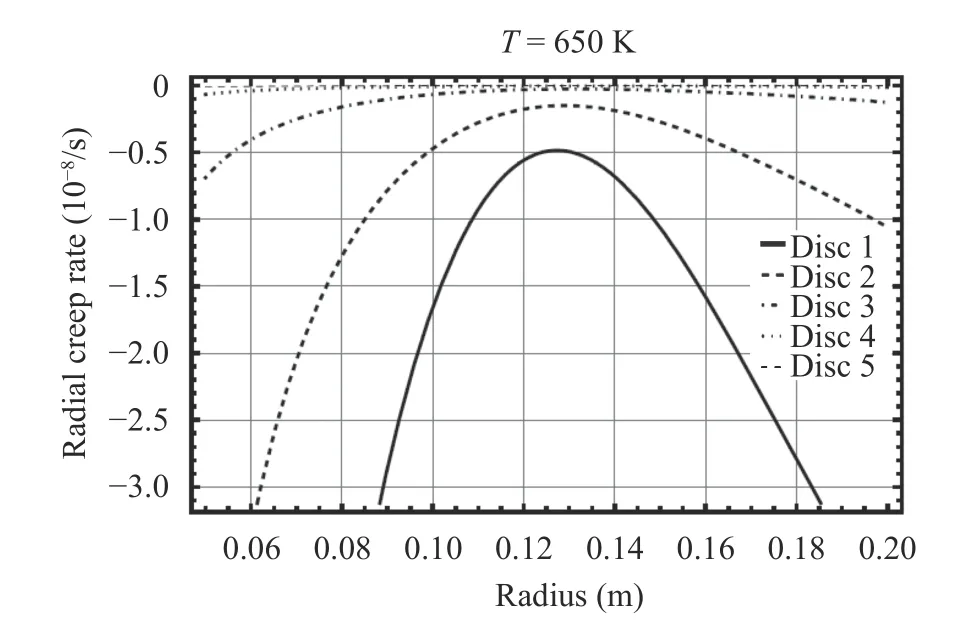
Fig. 7. Radial creep rate in different discs at T=650 K

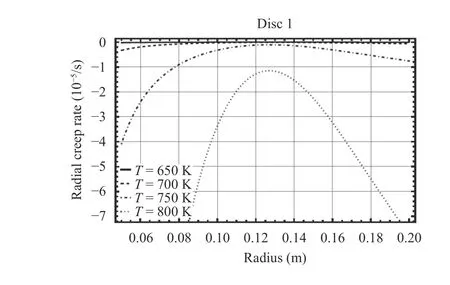
Fig. 8. Radial creep rate in disc 1 at various temperatures

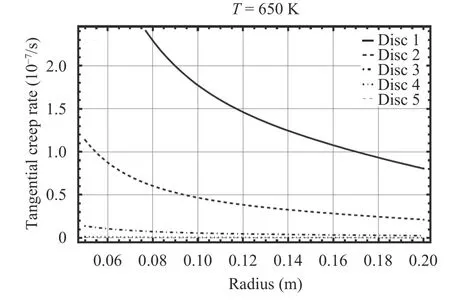
Fig. 9. Tangential creep rate in different discs at T=650 K

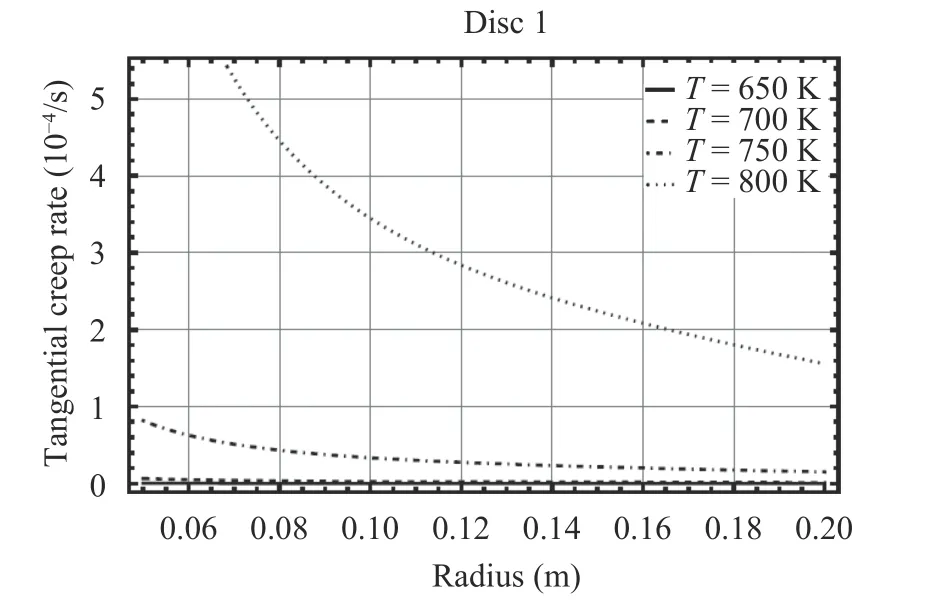
Fig. 10. Tangential creep rate in disc 1 at various temperatures

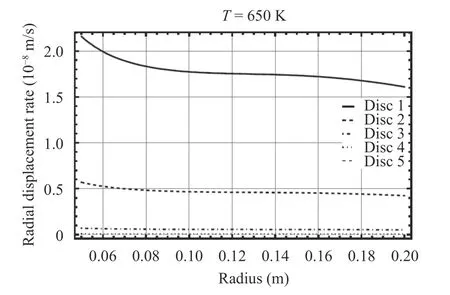
Fig. 11. Radial displacement rate in different discs at T=650 K

Here Kω2is the radial traction and K is a constant which mostly depends on the material, geometry and number of blades.Assuming an outside radial traction and using the developed formulations, the distribution of different stress and strain components can be obtained. Figure 12 shows the pattern of radial and tangential stresses across the radius of different rotating discs in the presence and absence of outside tractions.

In all cases the rotational speed is similar and equal to 1000 rad/s and the prevailing temperature is 700 K. The traction constant K is equal to 7.5 MPa·s2. As before, the number of discs points to the different amounts of ceramic particle contents. The graphs showing the distributions of radial and tangential creep rates are presented in Figs. 13 and 14.

All figures confirm that the inclusion of external traction will increase the levels of all stress and creep components in all case studies. The effects are more severe in the creep deformations than stress components. As it can be seen in Fig. 13, the patterns of particle distributions, designated by disc numbers, plays an important role in the trends of the graphs. Figure 14 shows how important is the effect of external traction upon the tangential component of creeping.

Fig. 12. a Radial stress and b tangential stress in presence and absence of traction

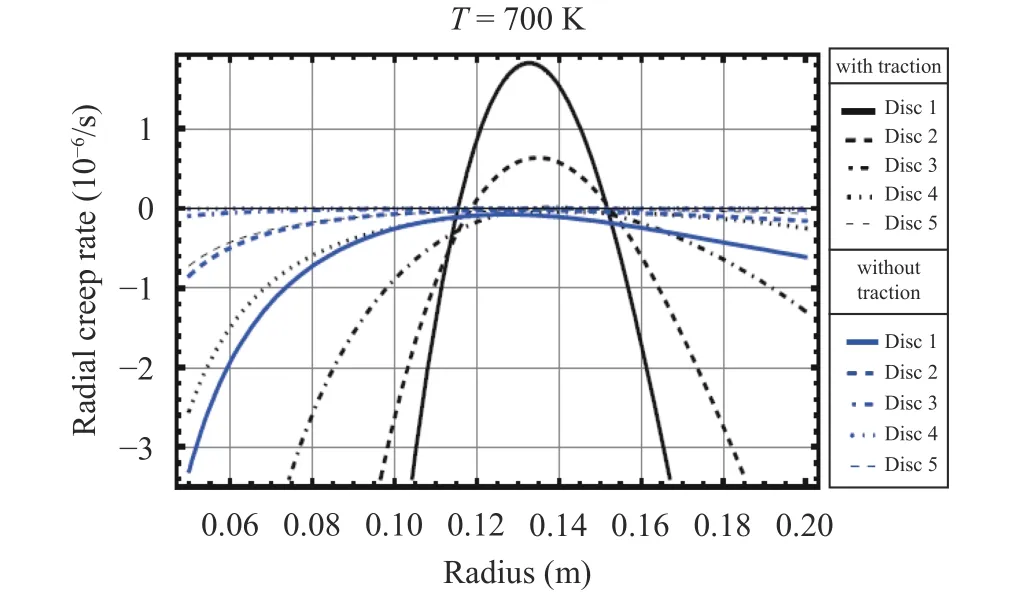
Fig. 13. Radial creep rate in presence and absence of traction

Another important factor worthwhile to be studied is the effect of external traction upon the deformation of the disc. Figure 15 is a graph of the disc deformation versus the level of traction or traction constant, K. Here the displacement rate in the outer radius of the disc is used as a measure of the disc deformation.The ordinate of the graph is in logarithmic scale. It means that this graph covers an extensive range of traction levels.

As it can be seen in Fig. 15 the more is the extent of particle contents, the less will be the effect of outside traction upon the deformation of the disc. This fact emphasizes that how important and valuable will be the usage of the inhomogeneous hubs for the turbine stages.

The steady state creep response of FGM rotating discs with different distributions of particle content and temperature, in the presence and absence of outer tractions is investigated. The analysis mainly encircles the situations where disc contains nonlinear patterns of distribution for the volume fraction or particle contents. Five different kinds of nonlinear particle distributions with similar values at the inner and the outer radii have been considered. The complete procedure of the mathematical modeling and solution techniques are represented. Results show that the type of particle distributions has significant effect on the stresses and strain rates. The discs with higher particle content show better responses. This means that in discs with bigger percentage of SiC particles the stresses and strain rates are lower than other discs. Tangential stress has a maximal at the inner radii, a decreasing trend throughout the disc and a minimal at the outer side. The radial stresses experience a maximum value in the middle of the disc. This result shows that the amount of particle content should be increased at the internal and external sides to guarantee the safety of the FGM discs. The study of the temperature confirms that its effect on the radial and tangential stresses is not significant, while it has high impact on the strains and creep strain rates and deformations. The effect of temperature is much serious in the discs with lower particle content than the discs with greater content of particles. It means that discs with lower particle content are more sensitive to the temperature changes. Moreover, the results show that external tractions can affect the creep rates and stress fields significantly. Especially, in presence of outlying tractions, it is shown that the discs with higher levels of particle content produce lower amounts of creep deformations.

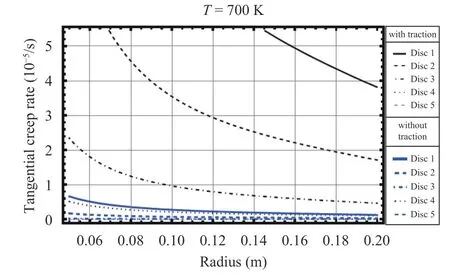
Fig. 14. Tangential creep rate in presence and absence of traction

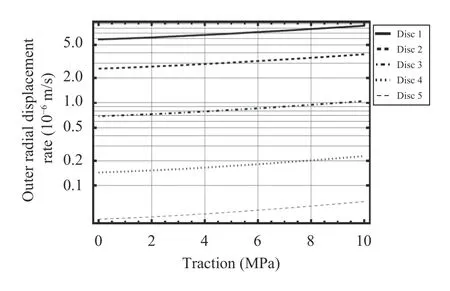
Fig. 15. Outer radial displacement via the level of traction