Generalized canonical transformation for second-order Birkhoffian systems on time scales

Y. Zhang, X.H. Zhai

a College of Civil Engineering, Suzhou University of Science and Technology, Suzhou 215011, China

b School of Science, Nanjing University of Science and Technology, Nanjing 210094, China

Keywords:Birkhoffian systems Generalized canonical transformation Time scales calculus Generating function

A B S T R A C T The theory of time scales, which unifies continuous and discrete analysis, provides a powerful mathematical tool for the study of complex dynamic systems. It enables us to understand more clearly the essential problems of continuous systems and discrete systems as well as other complex systems. In this paper, the theory of generalized canonical transformation for second-order Birkhoffian systems on time scales is proposed and studied, which extends the canonical transformation theory of Hamilton canonical equations. First, the condition of generalized canonical transformation for the second-order Birkhoffian system on time scales is established.Second, based on this condition, six basic forms of generalized canonical transformation for the second-order Birkhoffian system on time scales are given. Also, the relationships between new variables and old variables for each of these cases are derived. In the end, an example is given to show the application of the results.

The theory of time scales calculus unifies the continuous analysis, discrete analysis and quantum analysis, and provides a powerful mathematical tool for studying complex dynamical systems [1–3]. In practical problems, many processes sometimes depend on continuous time variables, sometimes on discrete time variables, while some processes have discrete time variables that are piecewise continuous. For these problems, the time scales calculus can be used to establish their mathematical models [4]. In recent years, dynamic modeling and its applications on time scales [5–9], symmetries and conserved quantities on time scales [10–16] and integral methods on time scales [17,18] have attracted a wide range of interests and achieved a series of results.

Transformation is an important method of the research of analytical mechanics. For general dynamical equations, it is often very difficult to solve. Therefore, making those equations into the differential equations which can be solved easily by using transformation method becomes a very important subject[19–21]. It is well known that the canonical transformation is one of the methods to achieve this goal. The Hamilton canonical equations remain invariant under canonical transformation.Birkhoffian mechanics is a natural development of Hamiltonian mechanics. However, the theory of Hamiltonian canonical transformation has not been widely applied to Birkhoffian systems [22–23]. In this paper, the theory of generalized canonical transformation for second-order Birkhoffian systems on time scales will be discussed. The transformation theories of Hamiltonian systems on time scales, classical Birkhoffian systems and Hamiltonian systems are special cases.

The second-order Birkhoff's equations [13] on time scales can be expressed as

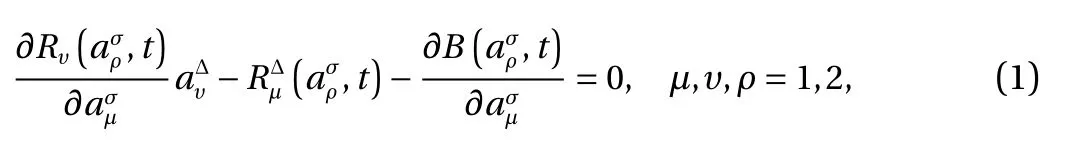
Introducing the isochronous transformation

if the Birkhoff's equations on time scales keep the form

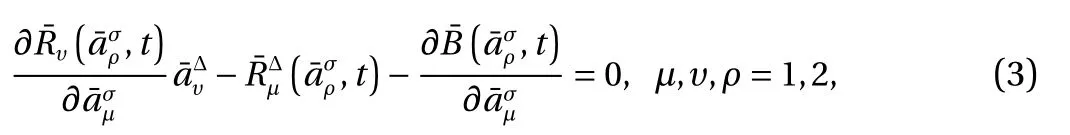
According to the Pfaff–Birkhoff principle [13] on time scales,both new variables and old variables satisfy

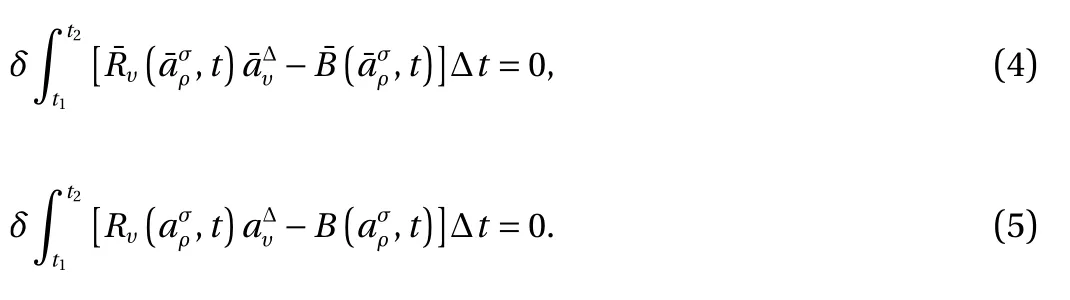
Equations (4) and (5) hold at the same time, but that does not mean that their integrands are exactly equal. The two integrands can differ by a delta total differential of an arbitrary functionwith respect to t.

Therefore, if both the new variables and old variables satisfy

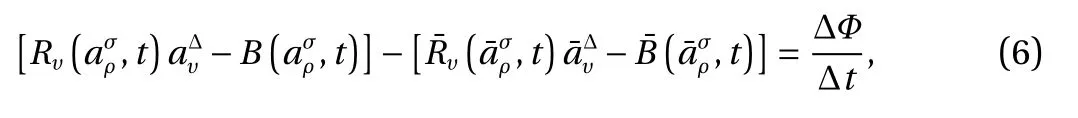
then Eq. (2) is the generalized canonical transformation for the second-order Birkhoffian system (1) on time scales. FunctionΦ can be called the generating function. It's worth mentioning that, the generating function Φ is a function with new variablesold variablesand t, and the variables are related to each other by transformation Eq. (2). Therefore, except for the time variable t, only two variables are independent. In general, there are different options to choose independent variables, but for one specific transformation, this choice is by no means arbitrary[19–21].

The relation Eq. (6) can also be written as

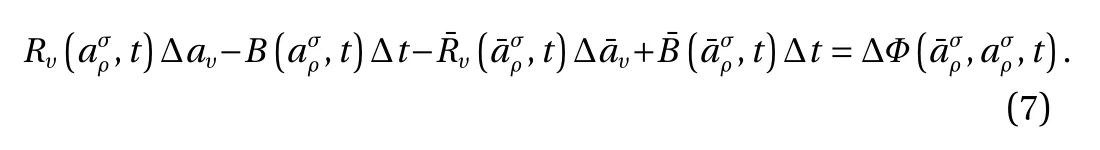
Now, the six basic forms of the generalized canonical transformations for second-order Birkhoffian systems on time scales are discussed below, and the corresponding transformation relations are derived.

(1) Generalized canonical transformation of the first form

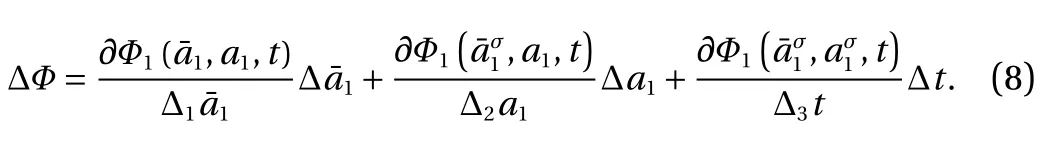
Substituting Eq. (8) into Eq. (7), we obtain

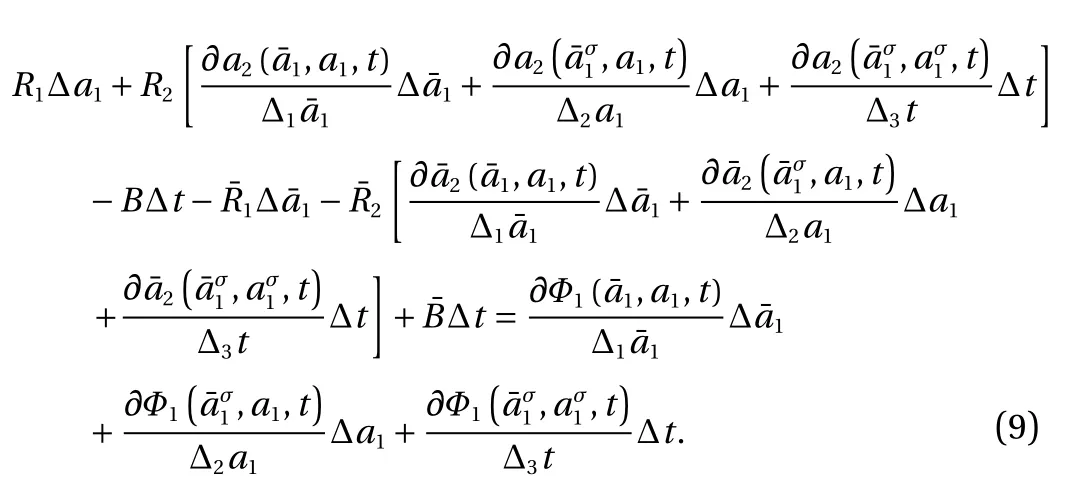
With considering the independence ofand ∆ t, from Eq. (9), we yield

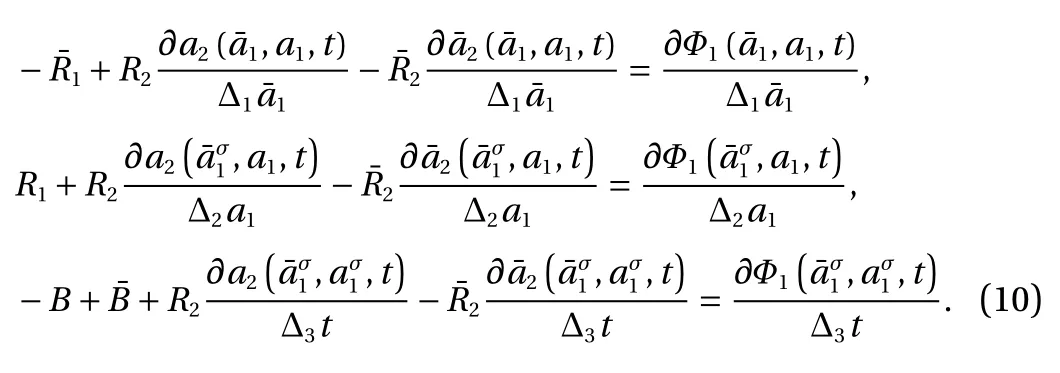
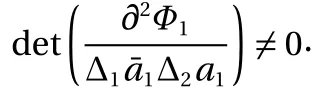
Equation (10) is the first form of transformation relation of generalized canonical transformation for second-order Birkhoffian systems. Two types of problems can be solved by Eq. (10).The first type is to construct new Birkhof's functions and new Birkhoffian with knowing generalized canonical transformation.The second type is to find generalized canonical transformation with knowing new Birkhof's functions and new Birkhoffian. The former needs to solve the algebraic Eq. (10) with respect toandwhereas, the latter neesds to solve the partial differential Eq. (10) with respect to. Obviously, the second one is more complicated.

(2) Generalized canonical transformation of the second form

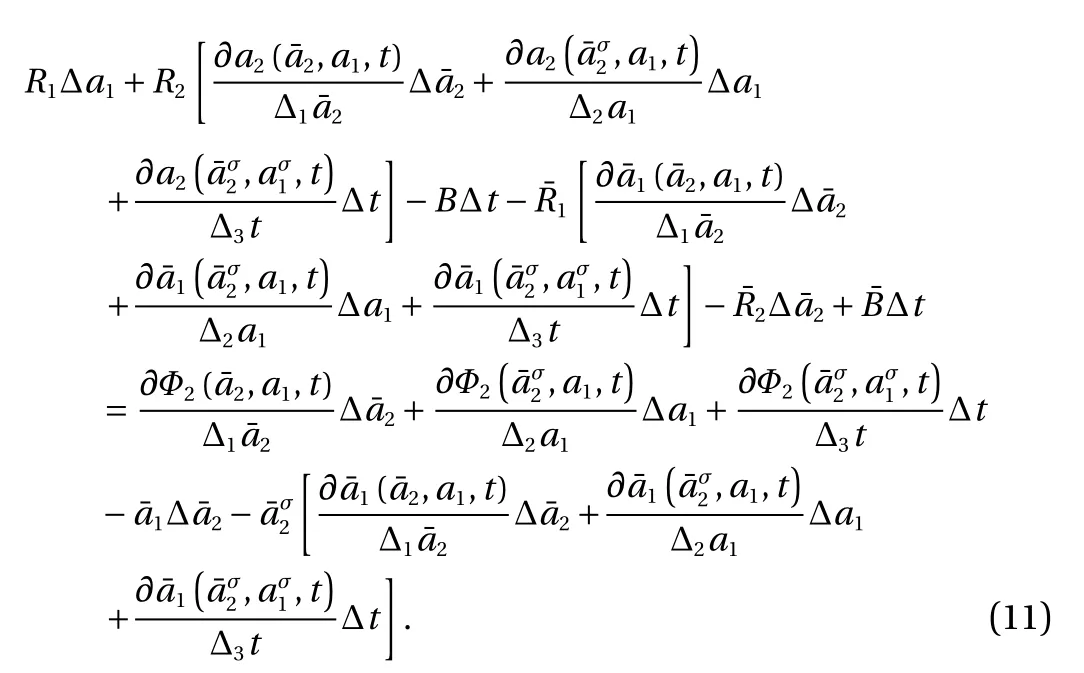
With considering the independence ofand ∆ t, we have the following transformation relation from Eq. (11)

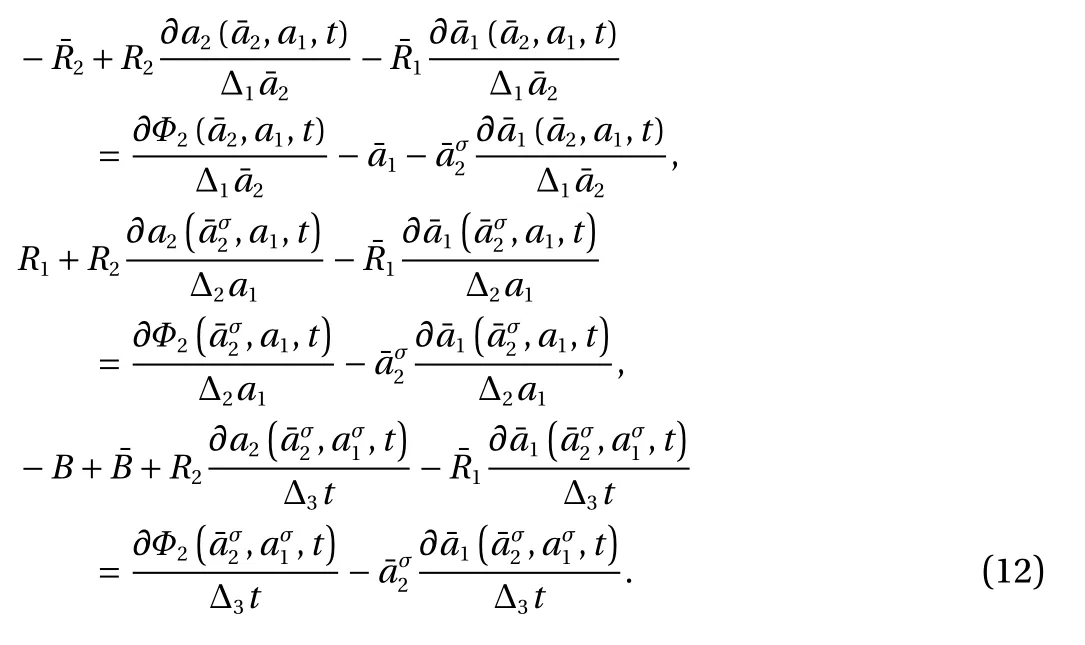
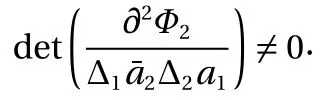
(3) Generalized canonical transformation of the third form

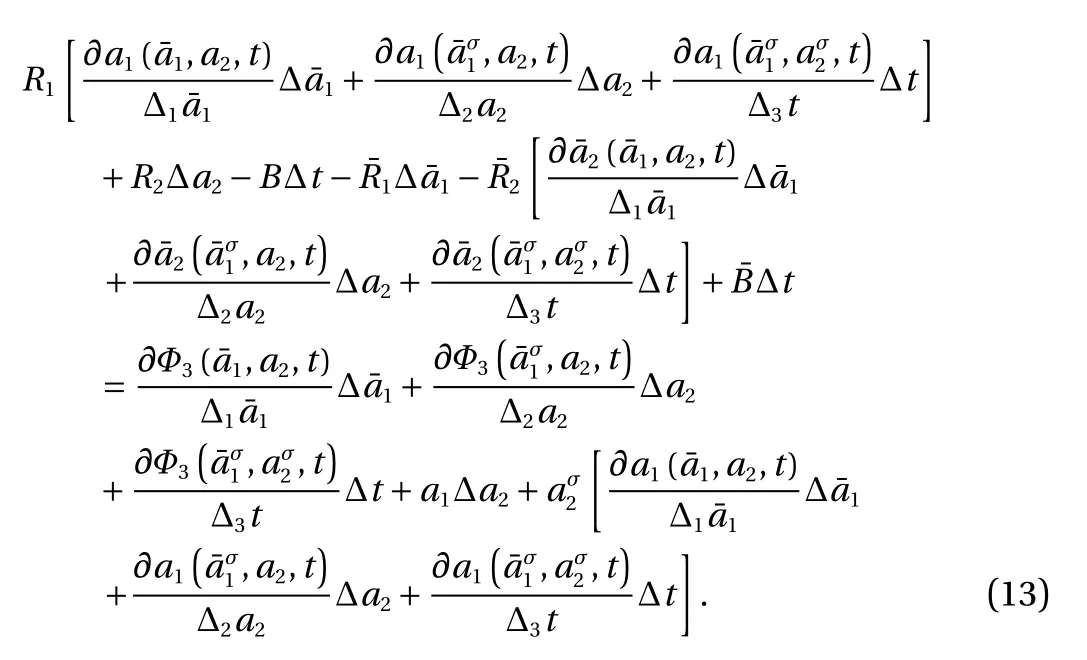
With considering the independence ofand ∆ t, we have the following transformation relation from Eq. (13)

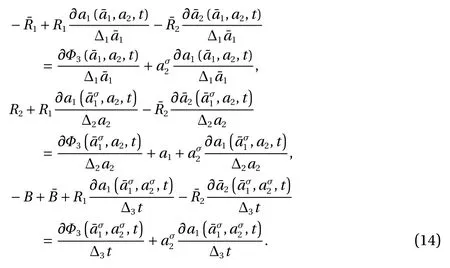
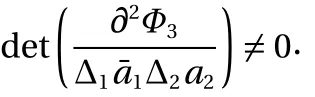
(4) Generalized canonical transformation of the fourth form

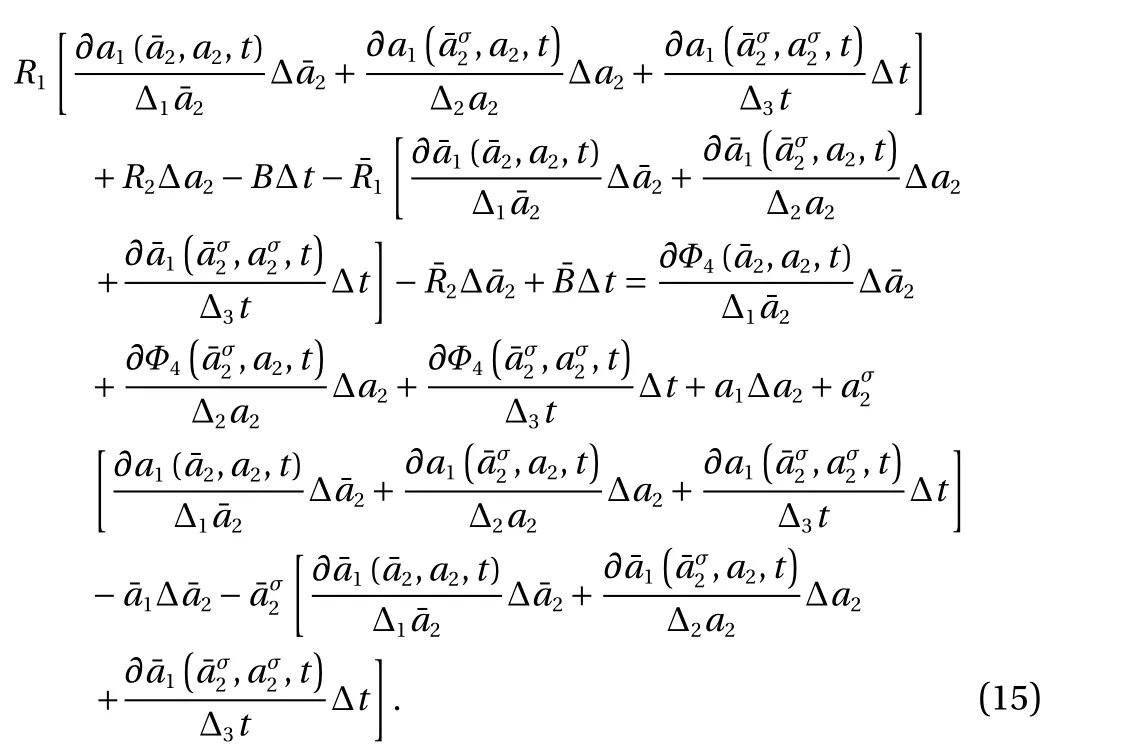
With considering the independence ofand ∆ t, we have the following transformation relation from Eq. (15)

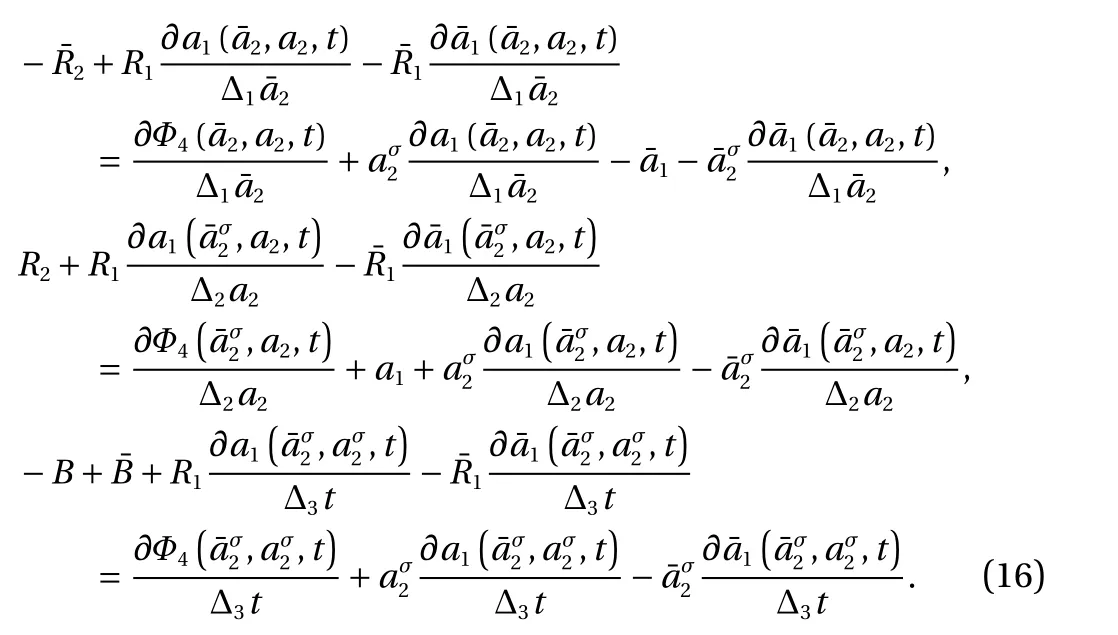
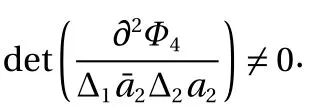
(5) Generalized canonical transformation of the fifth form

Suppose that a1, a2and t are independent variables, the generating function can be Φ = Φ5(a1,a2,t), then Eq. (7) becomes

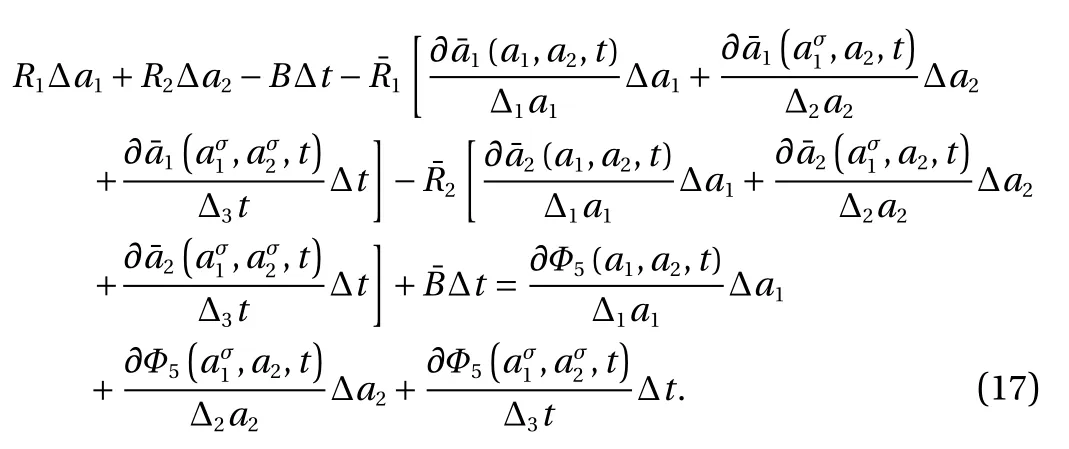
With considering the independence of ∆ a1, ∆ a2, and ∆ t, we have the following transformation relation from Eq. (17)

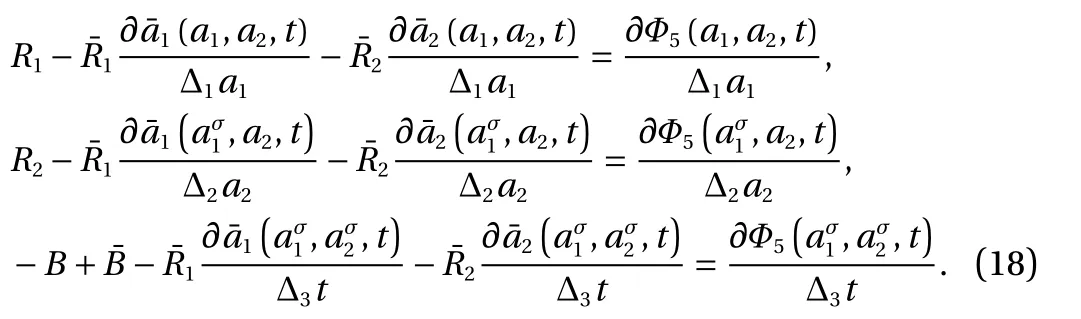
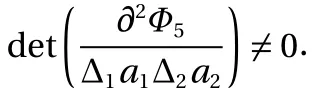
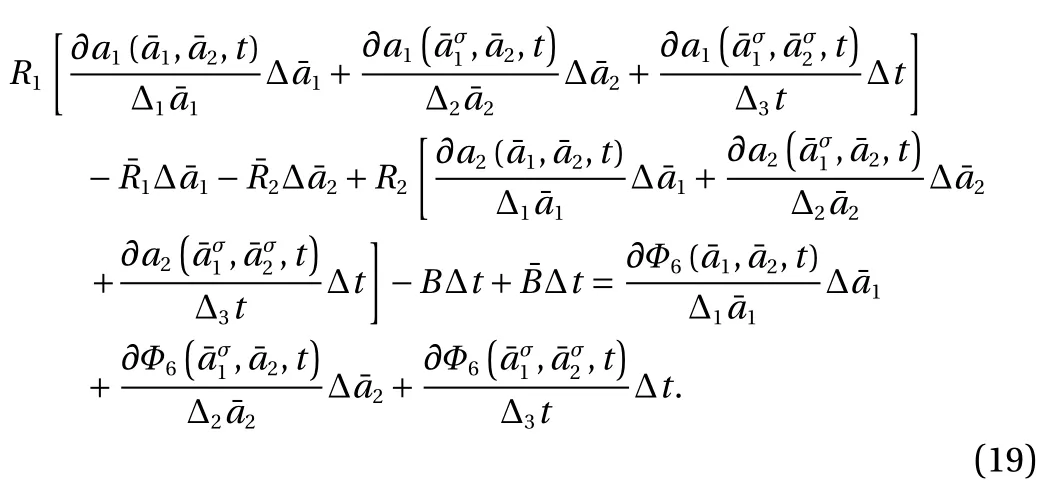
With considering the independence ofand ∆ t, we have the following transformation relation from Eq. (19)

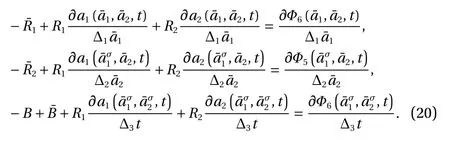
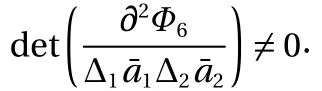
The six basic forms of generalized canonical transformations expressed by six kinds of generating functions above are just part of them. However, they are quite extensive.

If neither the generating function nor the generalized canonical transformation is explicitly contained t , thenand the condition Eq. (7) becomes

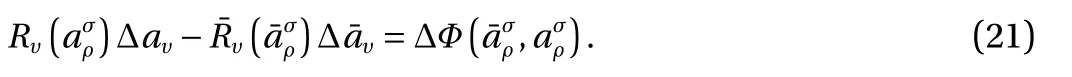
This kind of transformation can be called generalized contact transformation for Birkhoffian systems on time scales.

If a1= q , a2= p , R1= p, R2= 0, B = H , where q , p and H denote the generalized coordinate, generalized momentum and Hamiltonian, respectively, then the first four generalized canonical transformations mentioned above become the four basic forms of canonical transformations for Hamiltonian systems on time scales [18].

Example: Consider a second-order Birkhoffian system on time scale, Birkhoff's functions and Birkhoffian are

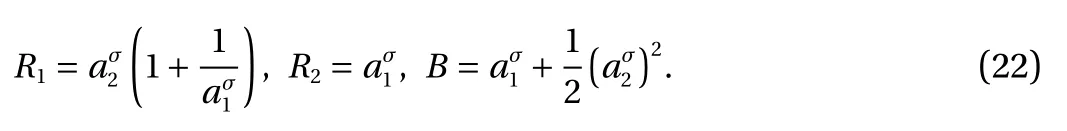
First, we calculate the forward jump operator σ (t) and the graininess function µ(t). Setthen we haveand µ (t)= σ(t)−t = t.

The Birkhoff's Eq. (1) on time scales give

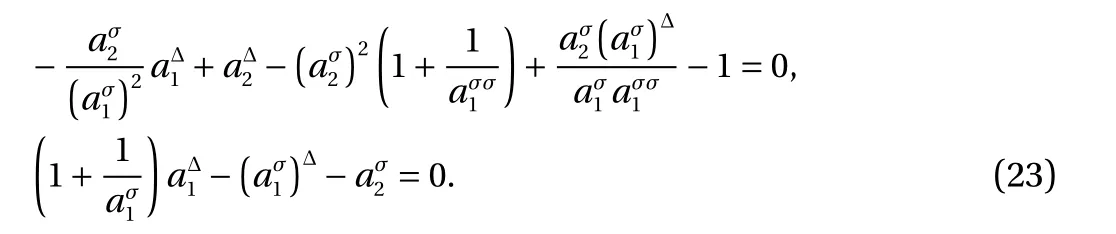
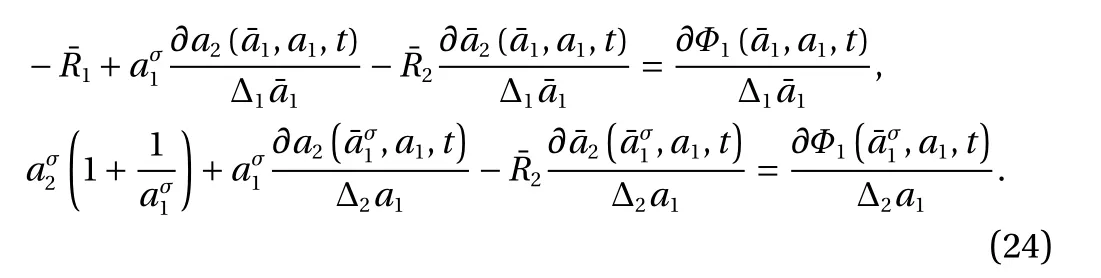
If the generalized canonical transformation isthen Eq. (41) gives

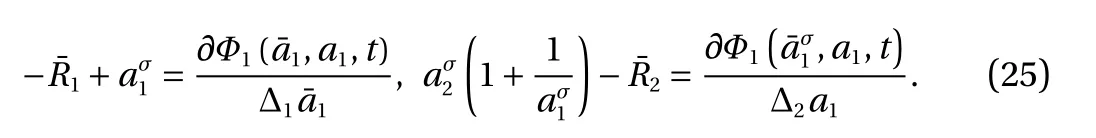
Clearly, the solution of Eq. (25) is not unique, if we choosethen Eq. (25) has the solution

According to the third equation of Eq. (10), we have

If we choose Φ1= 0, then

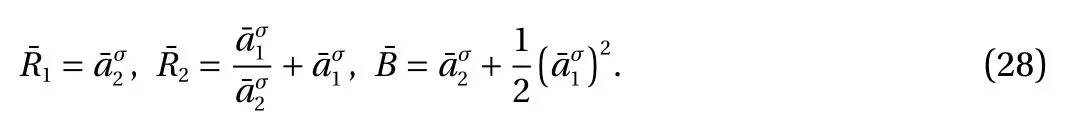
It is easy to know that the equations of the Birkhoffian system are invariant for the new Birkhoff's functions and the new Bikhoffian Eqs. (26)–(28).

In the past ten years, the theory of time scales calculus becomes more and more widely used in describing complex dynamic process. Transformation theory is an important aspect of the research of analytical mechanics. This article presented and studied the generalized canonical transformation for second-order Birkhoffian systems on time scales, six kinds of generating function are given by assuming independent variables. In the meantime, six basic forms of generalized canonical transformation and transformation relations were constructed from the selections of generating function. The example given is to illustrate the effectiveness of the results. The research of transformation theory for constrained mechanical systems on time scales is still an open question. Further works about the transformation theory for generally Birkhoffian systems on time scales and the Hamilton-Jacobi theory are still worth doing.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grants 11972241 and 11572212).