Modified slow-fast analysis method for slow-fast dynamical systems with two scales in frequency domain

Zhengdi Zhang, Zhangyao Chen, Qinsheng Bi

a Faculty of Science, Jiangsu University, Zhenjiang 212013, China

b Faculty of Civil Engineering and Mechanics, Jiangsu University, Zhenjiang 212013, China

Keywords:Two scales in frequency domain Modified slow-fast analysis method Bursting oscillations Bifurcation mechanism

A B S T R A C T A modified slow-fast analysis method is presented for the periodically excited non-autonomous dynamical system with an order gap between the exciting frequency and the natural frequency. By regarding the exciting term as a slow-varying parameter, a generalized autonomous fast subsystem can be defined, the equilibrium branches as well as the bifurcations of which can be employed to account for the mechanism of the bursting oscillations by combining the transformed phase portrait introduced. As an example, a typical periodically excited Hartley model is used to demonstrate the validness of the method, in which the exciting frequency is far less than the natural frequency. The equilibrium branches and their bifurcations of the fast subsystem with the variation of the slow-varying parameter are presented. Bursting oscillations for two typical cases are considered, which reveals that, fold bifurcation may cause the the trajectory to jump between different equilibrium branches, while Hopf bifurcation may cause the trajectory to oscillate around the stable limit cycle.

The study of the slow-fast dynamics may date back to the end of 19th century when the relaxation oscillations was found in a set of dynamical systems [1]. However, it was until the H-H model was established by the Nobel Prize winners, Hodgkin and Huxley [2], which can exhibit the bursting activities of the neuron behaviors that the slow-fast system has been receiving wide attention. Generally, the dynamics with the coupling of the two scales often behaves in bursting oscillations. Since there exits no valid analytical method, most of the early results were obtained based on the approximated approaches as well as the numerical simulations [3]. In order to explore the mechanism of the dynamics, the slow-fast analysis method proposed by Rinzel [4]was introduced, the main idea of which is to divide the whole system into two subsystems [5]. For a typical slow-fast dynamical system with one slow state variable, represented by [6]

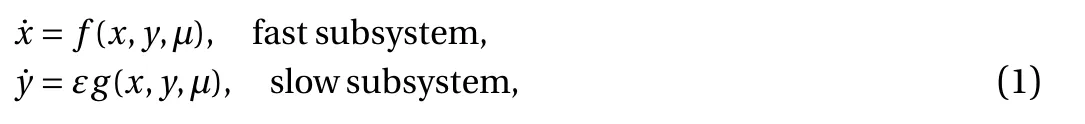
where x ∈ RM, y∈R, µ ∈ RK, while ε (0 < ε << 1) describes the ratio between the slow and fast scales.

The state variable y is considered as a slow-varying parameter, resulting in the equilibrium branches and their bifurcations of the fast subsystem with the variation the slowvarying parameter y, which can be used to determine the quiescent and spiking states as well as the bifurcations at the connections between the two states, while the modulation can be investigated by the slow-subsystem [7]. By overlapping the equilibrium branches and their bifurcation of the fast subsystem and the phase portrait of slow-fast dynamical system in the space (x, y), one may obtain the mechanism of the bursting oscillations. Upon the approach, many types of the bursting oscillations as well as the bifurcation mechanism have been reported, such as the pointpoint bursting oscillations [8], the point-cycle bursting attractors [9], a well list of which can be found in the late work by Izhikevich [10].

Up to now, most of the results are obtained based on the lowdimensional autonomous systems with two scales in time domain. When two scales in frequency domain involve the vector field, bursting oscillations can often be observed, the bifurcation mechanism cannot be obtained by the traditional slow-fast analysis method, since no obvious slow and fast subsystems can be defined. Here we propose a modified method to explore the mechanism of such types of bursting oscillations. For the nonautonomous systems with two scales in frequency domain, for example, the periodic excited oscillator, expressed in the form

with an order gap between the exciting frequency Ω and the natural frequency, denoted by ωN. When the exciting frequency is far less than the natural frequency, implying Ω << ωN, we can rewrite the equation in the form [11]

in which w is regarded as a generalized state variable. Since the state variables oscillate mainly according to the natural frequency, during each period corresponding to ωN, i.e., t ∈ [t0,t0+ 2π/ωN], w may change from WA= Asin(Ωt0) to WB= Asin[Ω(t0+ 2π/ωN)] = Asin(Ωt0+ 2πΩ/ωN), from which one may find that w keeps almost a constant [12]. Therefore, w can be considered as a slow-varying parameter.

Accordingly, one may obtain the equilibrium branches and their bifurcation of the fast subsystem in Eq. (3), which appears in a generalized autonomous system with the variation of w.

To reveal the mechanism of the bursting oscillations, we need to apply the bifurcations of the fast subsystem to the phase portrait of Eq. (3). For the purpose, here we introduce the conception of the transformed phase portrait. Since w is regarded as a generalized state variable, we define the transformed phase portrait as ΠG≡ [(x,w)|t ∈ R] = [x, Asin(Ωt)]|t ∈ R].

Overlapping the equilibrium branches and their bifurcations of the fast subsystem and the transformed phase portrait in the space (x, w), one may find the influence of the bifurcation of the fast subsystem on the bursting oscillations, described by the relationship between the real state variables x and the slow-varying parameter w.

To further explain the method, here we use the typical periodically excited Hartley model [13] as an example, which can expressed in the no-dimensional form as

where w = Asin(Ωt), f (x) = −αx −βx5−γtanh(δx).

For the fixed parameters at [14]

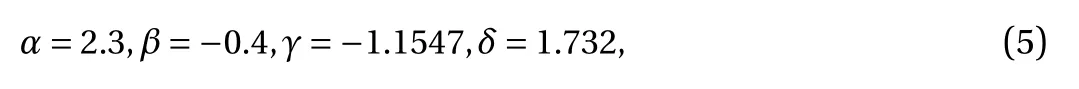
with w = 1.1sin(0.01t), w can be regarded as a slow-varying parameter, yielding the generalized autonomous fast subsystem in Eq. (4). Furthermore, w can also be considered as a generalized state variable, resulting in the transformed phase portrait, described by ΠG≡ [(x, y, z, w)|t ∈ R] = {[x, y, z,1.1sin(0.01t)]|t ∈ R}.

Obviously, the equilibrium points of generalized autonomous fast subsystem in Eq. (4) can be expressed in the form E0(x, y, z) = E0(−x0, 0, x0), where x0satisfies

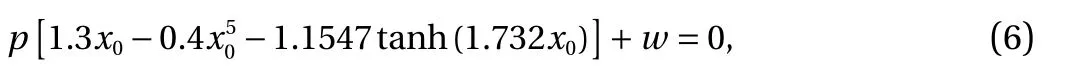
the stabilities of which can be determined by the associated characteristic equation, written as

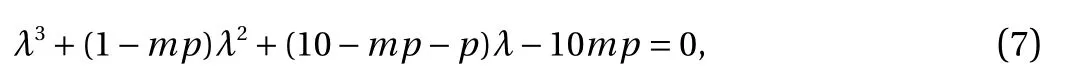
where m = −0.7 − 2x04+ 2tanh2(1.732x0).

From the characteristic Eq. (7), it can be found that fold bifurcation may occur at m = 0, yielding the following four sets, expressed by

at which jumping phenomena between different equilibrium points can be observed.

Similarly from Eq. (7), Hopf bifurcation may occur at sets HB1, defined by

at which Hopf bifurcation may take place, leading to periodic oscillations.

Now we focus on the bifurcation behaviors of different equilibrium points of the generalized autonomous fast subsystem Eq. (4), since the bifurcation may influence the behaviors of the structures of the bursting oscillations.

The fold and Hopf bifurcation sets are presented in Fig. 1, in which BTi(i = 1, 2, 3, 4) correspond Bautin bifurcations, while Si(i = 1, 2, 3, 4) separate the Hopf bifurcation between sub and super types. For the w values at the two points B and D in Fig. 1(b),denoted by wBand wD, respectively, when w < wD, super-Hopf bifurcation can be observed at HB1, while sub-Hopf bifurcation occurs at HB1for w > wD. Similarly, with the increase of w, sub-Hopf bifurcation takes place for w < wBand super-critical Hopf bifurcation occurs for w > wB.

Note that the bifurcation sets FBiand HBi(i = 1, 2) correspond to the fold and Hopf bifurcations related to different equilibrium points. For example, at the point HDin Fig. 1(b), located at the intersection of the two Hopf bifurcation sets, super-Hopf bifurcation occurs from one equilibrium point while sub-Hopf bifurcation takes place from another equilibrium point.

Now we fix the parameter p for two typical cases to explore the evolution of the dynamical behaviors of the fast subsystem with p = 5 and p = 5.8, respectively.

Figure 2 gives the equilibrium branch for p = 5, in which one may find that when w < −0.8862, only one stable focus can be observed, while at the point FA1,located at the fold bifurcation set FB1in Fig. 1(a), a cusp point appears, which may split into a stable and an unstable equilibrium points with the increase of w.Another fold bifurcation occurs when the equilibrium branch meets the set FB1in Fig. 1(a) at FB1for w = −0.5492, where two of the three equilibrium points join together to form a new cusp point. Jumping phenomena between different stable equilibrium points at both the two points FA1and FB1, while no Hopf bifurcation occurs because of no intersection point between the equilibrium branch and the Hopf bifurcation sets.

The phase portrait on the (x, y) plane is presented in Fig. 3, in which one may find that there exist four spiking states and four quiescent states in the bursting oscillations, denoted by SPiand QSi(i = 1, 2, 3, 4), respectively.

To reveal the mechanism of the bursting oscillations, we plot the overlap of transformed phase portrait and the equilibrium branches of the generalized autonomous fast subsystem in Fig. 4.

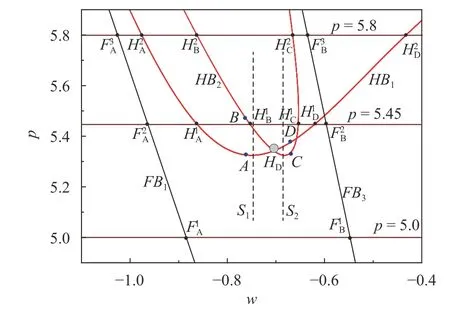
Fig. 1. Fold and Hopf bifurcation sets on the (w, p) plane.

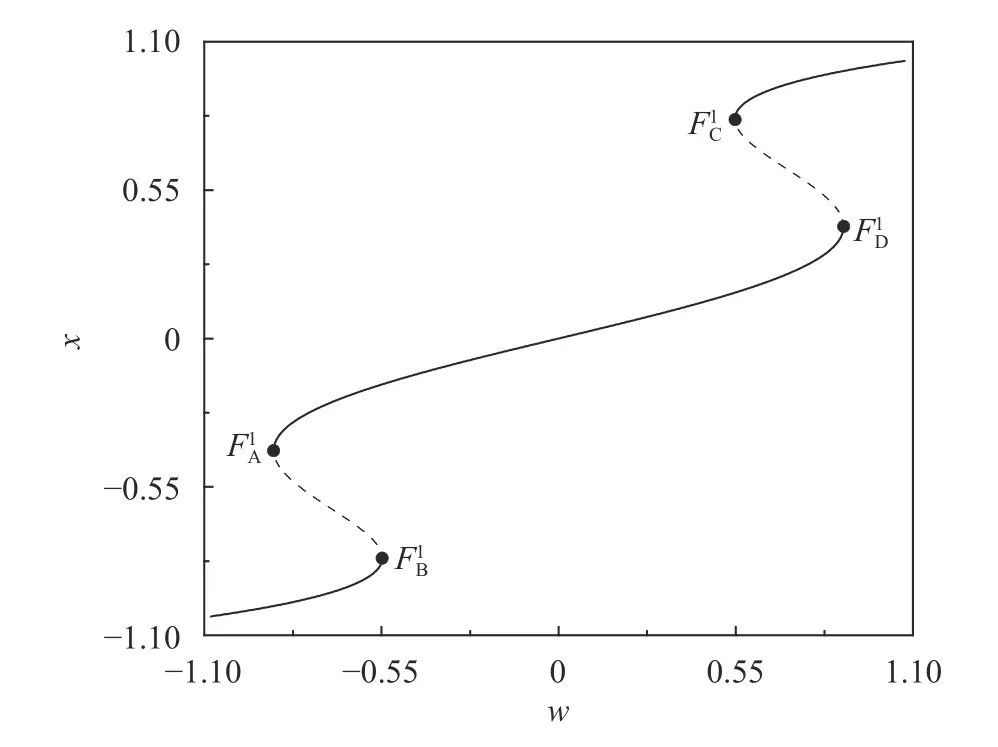
Fig. 2. Equilibrium branches and their bifurcations for p = 5 on the(w, x) plane with initial condition (x0, y0, z0) = (0.1, 0.1, 0.1).

From Fig. 4, one may find that, the trajectory, starting from the point A, at which w = −1.1, moves almost strictly along the stable equilibrium branch, behaving in the quiescent state QS1,until it arrives at the point FB1, at which fold bifurcation occurs,causing the trajectory to jump to the point B. Since the point B cannot be exactly located on the stable equilibrium branch EB,repetitive oscillations around EB take place to form the spiking state SP1. The oscillations may settle down to the stable EB at the point C, and then the trajectory moves almost strictly along the stable EB, leading to quiescent state QS2, until it reaches the point FD1, at which another fold bifurcation occurs, resulting in the jumping phenomenon of the trajectory to the point D. Repetitive oscillations around EQ takes places to form SP2, which may settle down to the stable EB. When the slow-varying w increases to w = +1.1, implying w reaches its maximum value, half period of the bursting oscillations is finished.

The other half period is symmetric to the above half period of the attractor, which we omitted here for simplicity.

According to the bifurcations between the quiescent states and the spiking states, the type of busting oscillations can be called periodic fold/fold/fold/fold bursting attractor. While from the geometric structure, it can also be called 4-point bursting attractor.

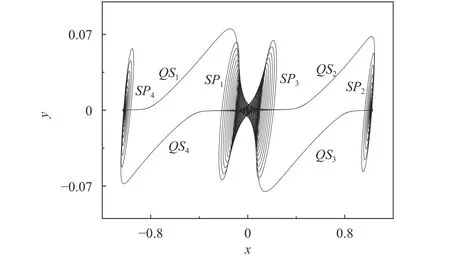
Fig. 3. Phase portrait on the (x, y) plane for p = 5.

Fig. 4. Overlap of the equilibrium branches of the fast subsystem and the transformed phase portrait on the (w, x) plane for p = 5.

Now we turn to the bursting oscillations for p = 5.8. Figure 5 gives the equilibrium branches and their bifurcations of the generalized autonomous fast subsystem.

From Fig. 5, one may find that, the equilibrium branches are divided into several segments by the bifurcation points. Further investigation reveals that the equilibrium branch segments AHB2, HC2FB3, FA3HA2, HD2HE2, HH2FD3, FC3HF2and CD are stable.

Sub-Hopf bifurcation may occur at the point HB2, leading an unstable limit cycle, which may collide with the stable limit cycle via super-Hopf bifurcation at the point HC2to form an fold limit cycle bifurcation.

Similarly, fold limit cycle bifurcation can also be observed when the stable limit cycle via super-critical Hopf bifurcation from HF2meets the unstable limit cycle from HG2.

Furthermore, two limit cycles via super-Hopf bifurcations at HA2and HH2respectively collide, while two unstable cycles via sub-Hopf bifurcations at HD2and HE2may also collide with the variation of w, which also results in fold limit cycle bifurcations.

Meanwhile, fold bifurcations can be observed at the four points FA3, FB3, FC3, FD3, leading to the transitions between the stable and unstable equilibrium branch segments. Figure 6 shows the phase portrait on the (x, y) plane for p = 5.8 for excited system, while Fig. 7 presents the time history of x of the attractor,from which one may find the trajectory may oscillate around limit cycles and the equilibrium points in turn, which is quite different from the attractor for p = 5 in Fig. 3. We turn to the overlap of the transformed phase portrait and the equilibrium branches and their bifurcations of the fast subsystem on the(w, x) plane in Fig. 8 for the bifurcation mechanism of the attractor.

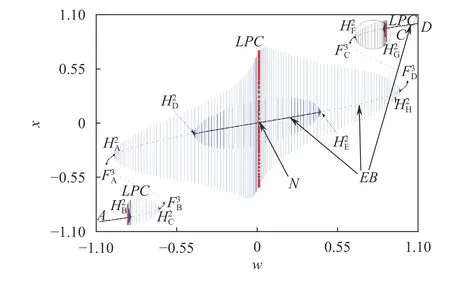
Fig. 5. Equilibrium branches and their bifurcations of the generalized autonomous fast subsystem for p = 5.8.

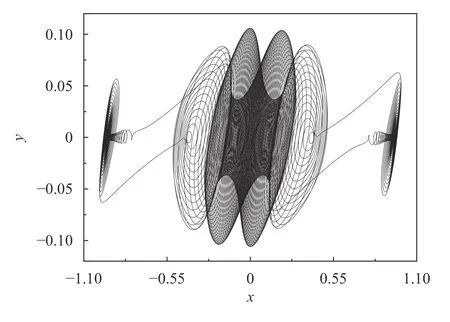
Fig. 6. Phase portrait of the bursting attractor on the (x, y) plane for p = 5.8 with the initial condition (x0, y0, z0) = (0.1, 0.1, 0.1).

The trajectory, starting form the point A with w = −1.1, moves almost strictly along the stable equilibrium branch AHB2, the unstable equilibrium segment HB2HC2, the stable equilibrium segment HC2FB3, behaving in the quiescent state QS1.

Fold bifurcation occurs at the point FB3, leading to the jumping phenomenon of the trajectory, resulting in the repetitive spiking oscillations with large amplitudes SP1, since only stable limit cycle via super-Hopf bifurcation at the point HA2exists.

Further investigation reveals that the repetitive spiking stage SP1oscillates in quasi-periodic type because of the influence of the two stable limits bifurcate from the two points HA2HH2, respectively.

The amplitudes of the oscillations may gradually decrease when w reaches the Hopf bifurcation point HH2, and the trajectory then settles down to the stable equilibrium branch segment HG2FD3, leading to the quiescent state QS1.

Fold bifurcation at FD3causes the trajectory to jump to the stable equilibrium branch segment CD. The transient process of the trajectory to the stable segment forms the spiking state SP2in Fig. 7.

Fig. 7. Time history of x for p = 5.8 with the initial condition(x0, y0, z0) = (0.1, 0.1, 0.1).

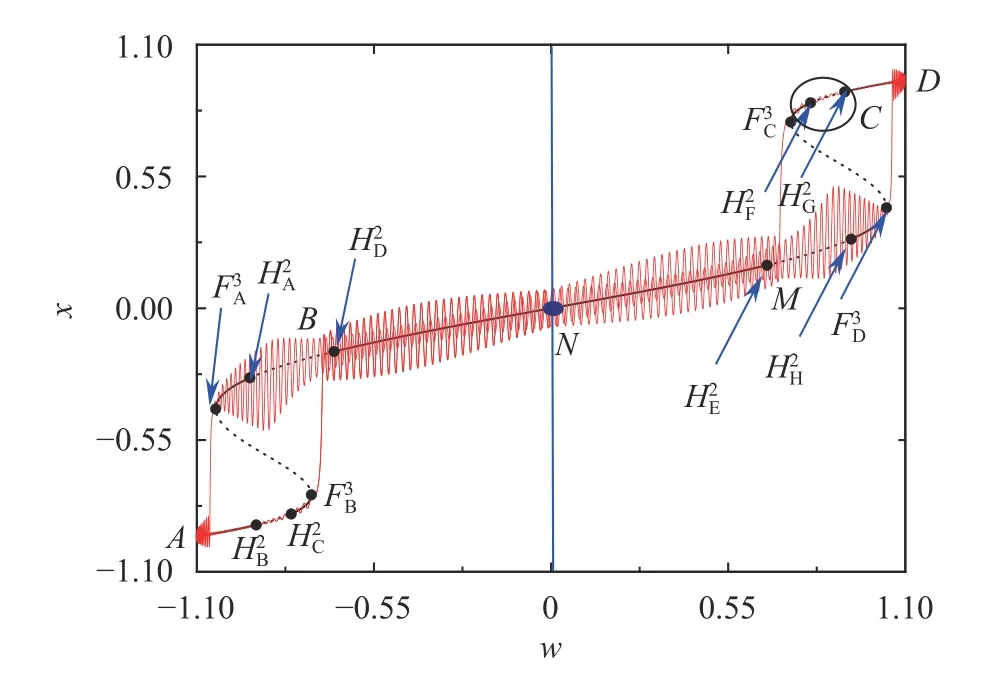
Fig. 8. Overlap of the equilibrium branches of the fast subsystem and the transformed phase portrait on the (w, x) plane for p = 5.8.

When the trajectory arrives at the point D with w = +1.1, half period of the bursting oscillations is finished. Because of the symmetry of the attractor, the other half period is omitted here for simplicity.

According to the bifurcations of the bursting attractor, the type of bursting oscillations can be called periodic fold/Hopf/Hopf/fold bursting attractor.

The effect of two time scales can be observed in periodically excited dynamical systems, behaving in bursting oscillations when an order gap exists between the natural frequency and the excited frequency. A modified method is presented, which can be used to reveal the mechanism of the bursting oscillations.

When the excited frequency is far less than the natural frequency, the whole excited term Asin(Ωt) can be regarded as a slow-varying parameter, resulting in the generalized autonomous fast subsystem. By introducing the transformed phase portrait of the attractor, the equilibrium branches and their bifurcations can be employed to account for the mechanism of the bursting oscillations. The validness of the method is demonstrated by the typical periodically excited Hartley model. It is found that, with the variation of the parameters, different types of the bifurcations may involve the vector field, leading to different types of bursting attractors. It is also noted that the trajectory may move along the unstable equilibrium branch segment because of the delay effect of the two bifurcation points on the branch, the distance between which is very small. Furthermore,fold limit cycle bifurcation caused by the interaction two stable limit cycles may lead to the quasi-periodic type spiking oscillations.

Acknowledgement

The authors are thankful to editors and referees for the careful reading and valuable suggestions that improve the quality and description of this manuscript. This work was supported by the National Natural Science Foundation of China (Grants 11632008 and 11872189).