On time independent Schrödinger equations in quantum mechanics by the homotopy analysis method

Jyotirmoy Rn, Shijun Lio,b,c,*

a School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, China

b State Key Laboratory of Ocean Engineering, Shanghai 200240, China

c School of Physics and Astronomy, Shanghai Jiao Tong University, Shanghai 200240, China

Keywords:Schrödinger equations Homotopy analysis method Convergent eigenvalues and eigenfunctions

A B S T R A C T A general analytic approach, namely the homotopy analysis method (HAM), is applied to solve the time independent Schrödinger equations. Unlike perturbation method, the HAM-based approach does not depend on any small physical parameters, corresponding to small disturbances.Especially, it provides a convenient way to gain the convergent series solution of quantum mechanics. This study illustrates the advantages of this HAM-based approach over the traditional perturbative approach, and its general validity for the Schrödinger equations. Note that perturbation methods are widely used in quantum mechanics, but perturbation results are hardly convergent. This study suggests that the HAM might provide us a new, powerful alternative to gain convergent series solution for some complicated problems in quantum mechanics, including many-body problems, which can be directly compared with the experiment data to improve the accuracy of the experimental findings and/or physical theories.

In quantum mechanics, the Schrödinger equations [1-7] govern the most interesting problems, such as harmonic and anharmonic oscillators, Morse and Pöschl-Teller potentials, etc. The perturbation methods have been developed and broadly applied to solve many problems in quantum mechanics and quantum chromodynamics (QCD) [1-9]. However, in most cases, accurate approximations can be gained only for physical quantities in a rather small range. The perturbation methods depend on a small physical parameter, i.e. perturbed parameter related to disturbances. In general, perturbation methods fail to give a accurate enough solution for large disturbances far from a known status. So do other traditional analytic approximation methods. In practices, a perturbation result is often used to check experimental data without verifying the convergence of the perturbation series solution. So, it is important to provide convergent results for large enough disturbances, which can be directly used to verify experimental data.

To overcome the limitations of perturbation methods and other traditional analytic methods, a general analytical approach, namely the homotopy analysis method (HAM), was proposed by Liao [10-12] using homotopy, a basic concept in topology. Unlike the perturbation methods, the HAM can solve a nonlinear equation without considering any small/large physical variables/parameters. Especially, the HAM gives a straightforward way to guarantee the convergence of solution series, and due to this, accurate approximations are always obtained even for strongly nonlinear equations. Besides, unlike all other analytical approximation methods, the HAM has a great freedom to choose the auxiliary linear operator and the initial guess of unknowns. The HAM has been widely applied to solve many strongly non-linear equations in different areas [13-18]. Note that the HAM has been used to gain new solutions of some highly nonlinear problems, which can not be obtained by other analytic methods even as well as numerical methods [12]. All of these illustrate the validity, novelty value and superiority of the HAM over all other analytic approximation methods.

Recently, a HAM-based approach was proposed by Liao [18]to solve the time independent Schrödinger equation in quantum mechanics, i.e.

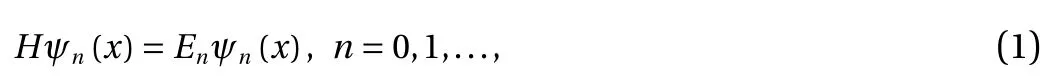
where H is a Hamiltonian operator, Enand ψn(x) are the unknown eigenvalue and the eigenfunction of H, respectively.Here, we assume that each eigenvalue Encorresponds to an unique eigenfunction ψn(x). The anharmonic oscillator was used by Liao [18] as an example to illustrate the validity of this approach.

In this manuscript, two examples in quantum mechanics are further used to illustrate the general validity of the HAM-based approach proposed by Liao [18]. The mathematical formulas of this HAM-based approach are briefly described, then we show two examples to verify the validity of this approach.

Liao [18] assumed that the eigenfunction ψn(x) can be expressed by the set of known eigenfunctionsatisfying

where H0is a known Hamiltonian operator,andare the corresponding known eigenvalue and the eigenfunction of H0,respectively. Assume that each eigenvaluecorresponds to an unique eigenfunction, and besidesis orthonormal,i.e.

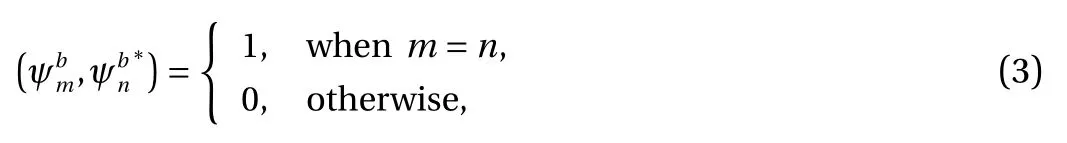
The homotopy series solution of the time independent Schrödinger equation read

where

with N being a large enough truncation number and

in which

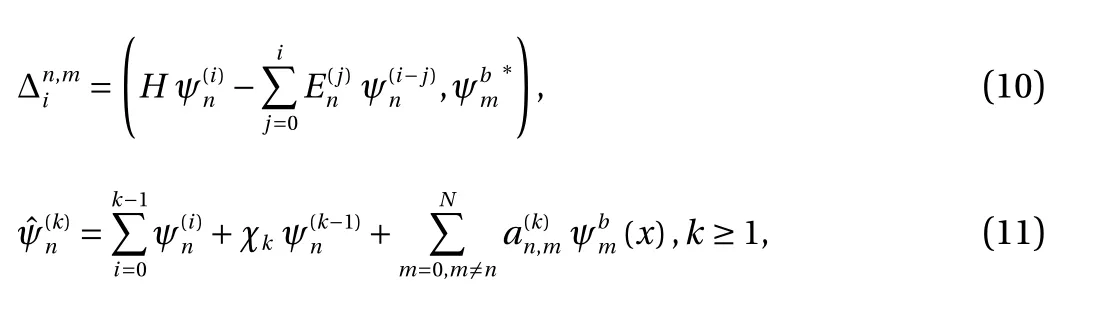
and

Especially, c0is the so-called “convergence-control parameter” in the frame of the HAM, which can guarantee the convergence of solution series. The optimal value of the c0is determined by means of the minimum of the residual error square of the governing Eq. (1). This is quite different from all other analytic approximation methods. In fact, it is the so-called "convergencecontrol parameter" c0that distinguishes the HAM from all of others. For details, please refer to Liao [18].

At the Mth-order of approximation, we have

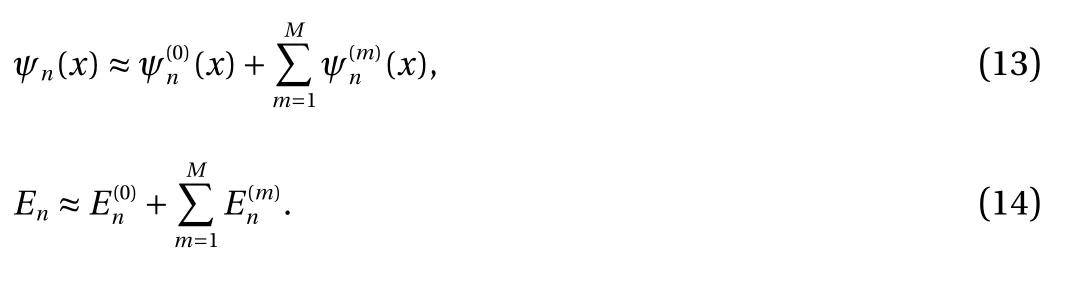
Unlike perturbation methods, the HAM provides us the great flexibility to choose the initial guessUsing this freedom,we can first chooseand then gain a Mth-order approximation of ψnand Enby means of the above-mentioned formulas. Then, the Mth-order approximation of ψncan be further used as an initial guessto gain a better M th-order approximation of ψnand Enin a similar way. In fact, this provides us a iteration HAM-based approach for the considered problem, which can accelerate the convergence greatly, as illustrated by Liao [18].

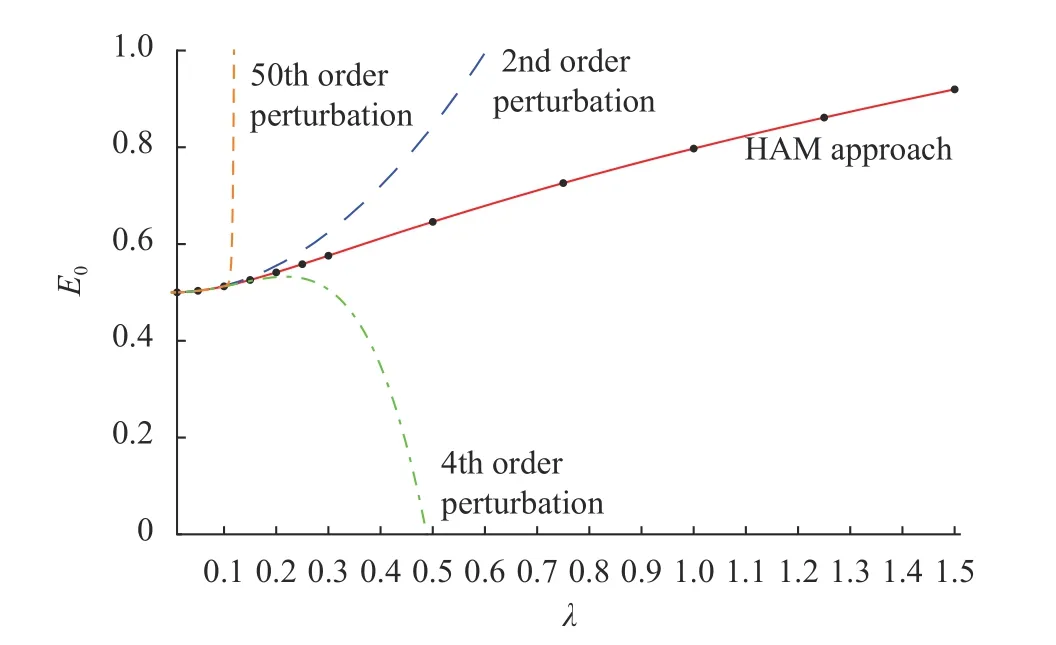
Fig. 1. The analytic approximations of the eigenvalue E0 of Eq. (15)versus λ. Solid line: convergent results given by the HAM-based approach; long dashed line: 2nd-order perturbative approach; dasheddotted line: 4th-order perturbative approach; dashed line: 50th-order perturbative approach.

Table 1 The analytic approximations of the eigenvalue and residual error square of Eq. (15) using 6th-order HAM-based iteration approach at different times of iteration in case of with, and with,, compared by the perturbation approach at different order of approximation.

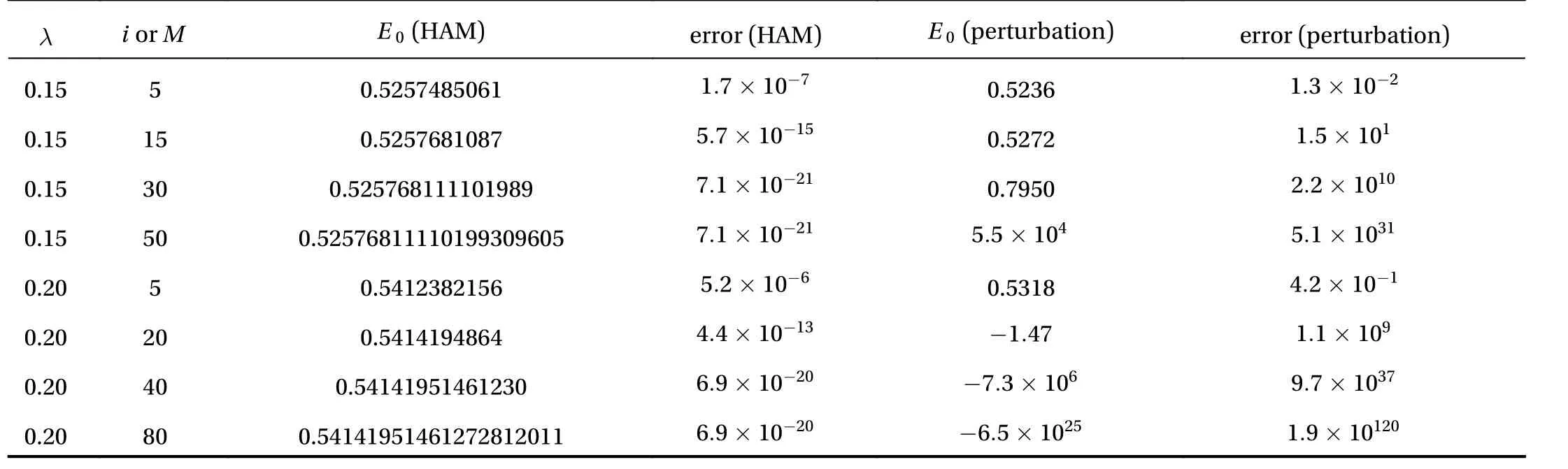
Table 1 The analytic approximations of the eigenvalue and residual error square of Eq. (15) using 6th-order HAM-based iteration approach at different times of iteration in case of with, and with,, compared by the perturbation approach at different order of approximation.

images/BZ_47_177_615_198_644.pngimages/BZ_47_295_611_308_641.pngimages/BZ_47_355_611_392_640.pngor images/BZ_47_661_606_703_644.pngimages/BZ_47_1448_606_1490_644.png(perturbation) error (perturbation)0.15 5 0.5257485061(HAM) error (HAM)images/BZ_47_1124_680_1282_718.png0.5236images/BZ_47_1966_680_2124_718.png0.15 15 0.5257681087 0.15 30 0.525768111101989 0.15 50 0.52576811110199309605 0.20 5 0.5412382156 0.20 20 0.5414194864 0.20 40 0.54141951461230images/BZ_47_1117_751_1288_788.pngimages/BZ_47_1117_822_1288_859.pngimages/BZ_47_1117_893_1288_930.pngimages/BZ_47_1124_963_1282_1001.pngimages/BZ_47_1117_1034_1288_1072.pngimages/BZ_47_1117_1105_1288_1143.png0.5272 0.7950images/BZ_47_1511_893_1653_930.png0.5318images/BZ_47_1536_1040_1628_1074.pngimages/BZ_47_1499_1105_1665_1143.pngimages/BZ_47_1974_751_2116_788.pngimages/BZ_47_1968_822_2122_859.pngimages/BZ_47_1968_893_2122_930.pngimages/BZ_47_1966_963_2124_1001.pngimages/BZ_47_1974_1034_2116_1072.pngimages/BZ_47_1968_1105_2122_1143.png0.20 80 0.54141951461272812011images/BZ_47_1117_1176_1288_1213.pngimages/BZ_47_1492_1176_1672_1213.pngimages/BZ_47_1962_1176_2128_1213.png

In this study, we further consider two examples in the quantum mechanics, the complex cubic anharmonic oscillator and the perturbed Pöschl-Teller potential, to show the general validity of the HAM-based approach developed by Liao [18].These two examples are widely used in textbooks of quantum mechanics. Unlike the perturbative approach [1-7], the HAMbased approach successfully provides the accurate convergent results for eigenvalues and eigenfunctions, as shown below.

The non-dimensional form of the time independent Schrödinger equation for a complex cubic anharmonic oscillator is given by [19]

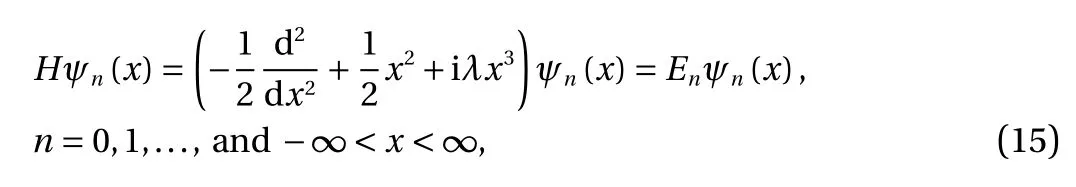
with an orthonormal basis

Table 2 The convergent results of the eigenvalue of Eq. (15)given by the HAM-based approach for different values of by means of the appropriate values of and.

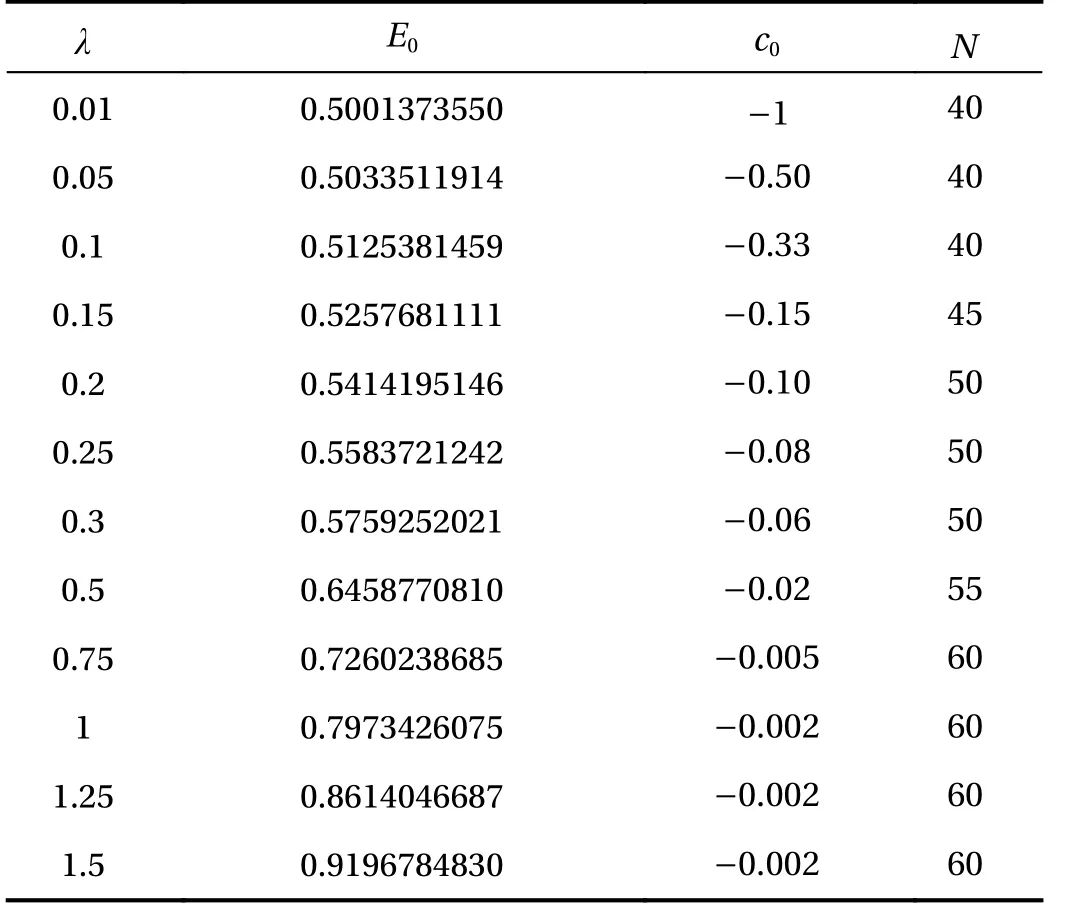
Table 2 The convergent results of the eigenvalue of Eq. (15)given by the HAM-based approach for different values of by means of the appropriate values of and.

E0 c0 N 0.01 0.5001373550 −1 40 0.05 0.5033511914 −0.50 40 0.1 0.5125381459 −0.33 40 0.15 0.5257681111 −0.15 45 0.2 0.5414195146 −0.10 50 0.25 0.5583721242 −0.08 50 0.3 0.5759252021 −0.06 50 0.5 0.6458770810 −0.02 55 0.75 0.7260238685 −0.005 60 1 0.7973426075 −0.002 60 1.25 0.8614046687 −0.002 60 1.5 0.9196784830 −0.002 60 λ

Even in case of small disturbances, such as λ = 0.15 and 0.2,the residual error square of perturbation series increases quite significantly (see Table 1) and the perturbation series are divergent. It is found that the perturbation series is divergent for λ ≥0.1, as shown in Fig. 1. However, by means of 6th-order HAM based iteration approach for λ = 0.15 and 0.2, the residual error square decreases sharply as the times of iteration increases,and convergent results of E0are obtained as 0.52576811110199309605 and 0.54141951461272812011, respectively, in accuracy of 20 digits. These HAM results agree with the results obtained by means of the homotopy-Padé technique [10,12, 18]. The convergent HAM based results of E0are shown in Fig. 1 and Table 2. This shows the validity as well as superiority of the HAM-based approach over the perturbation approach for the time independent Schrödinger equations.

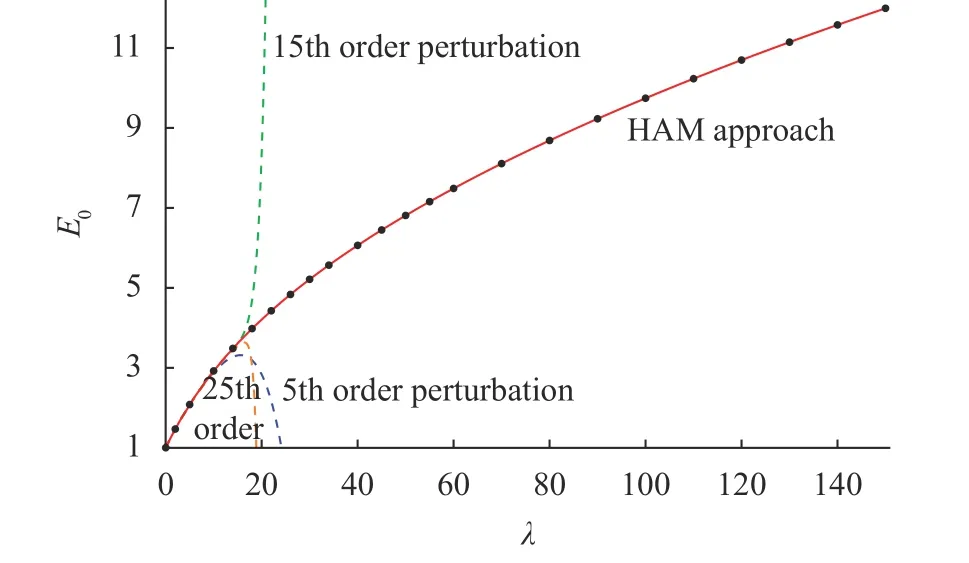
Fig. 2. Comparison of analytic approximations of the eigenvalue of Eq. (19) for different values of when. Solid line: convergent results given by the HAM-based approach; solid circle: numerical results; long dashed line: the 5th-order perturbative result;dashed line: the 15th-order perturbative result; dashed dot dotted line: the 25th-order perturbative result.

Note that as the disturbance becomes larger, we should use a larger truncation number N and a convergence-control parameter c0closer to zero. This has general meaning.

The non-dimensional time-independent Schrödinger equation for perturbed Pöschl-Teller potential is given by Ciftci et al. [8]

Table 3 The eigenvalue and residual error square of Eq. (19) in case of and or 20 at different orders of approximation given by the HAM-based approach using and or, respectively, compared with perturbation results.

Table 3 The eigenvalue and residual error square of Eq. (19) in case of and or 20 at different orders of approximation given by the HAM-based approach using and or, respectively, compared with perturbation results.

Table 4 The convergent results of eigenvalues and of Eq. (19) at = 0 for different values of by means of the HAM-based approach using and the appropriate values of.

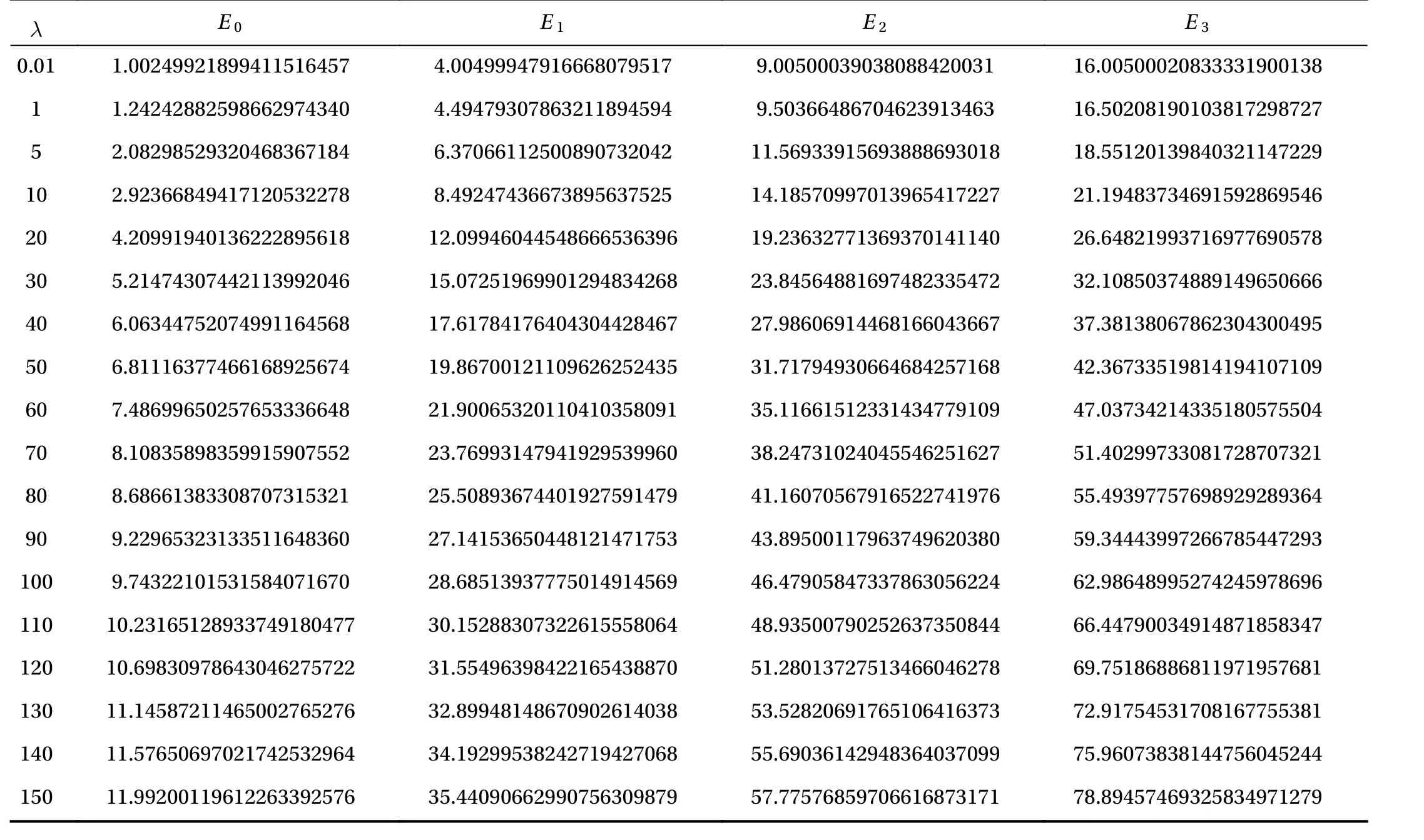
Table 4 The convergent results of eigenvalues and of Eq. (19) at = 0 for different values of by means of the HAM-based approach using and the appropriate values of.

Table 5 The convergent results of eigenvalues and of Eq. (19) at = 0.5 for different values of by means of the HAM-based approach using and the appropriate values of.

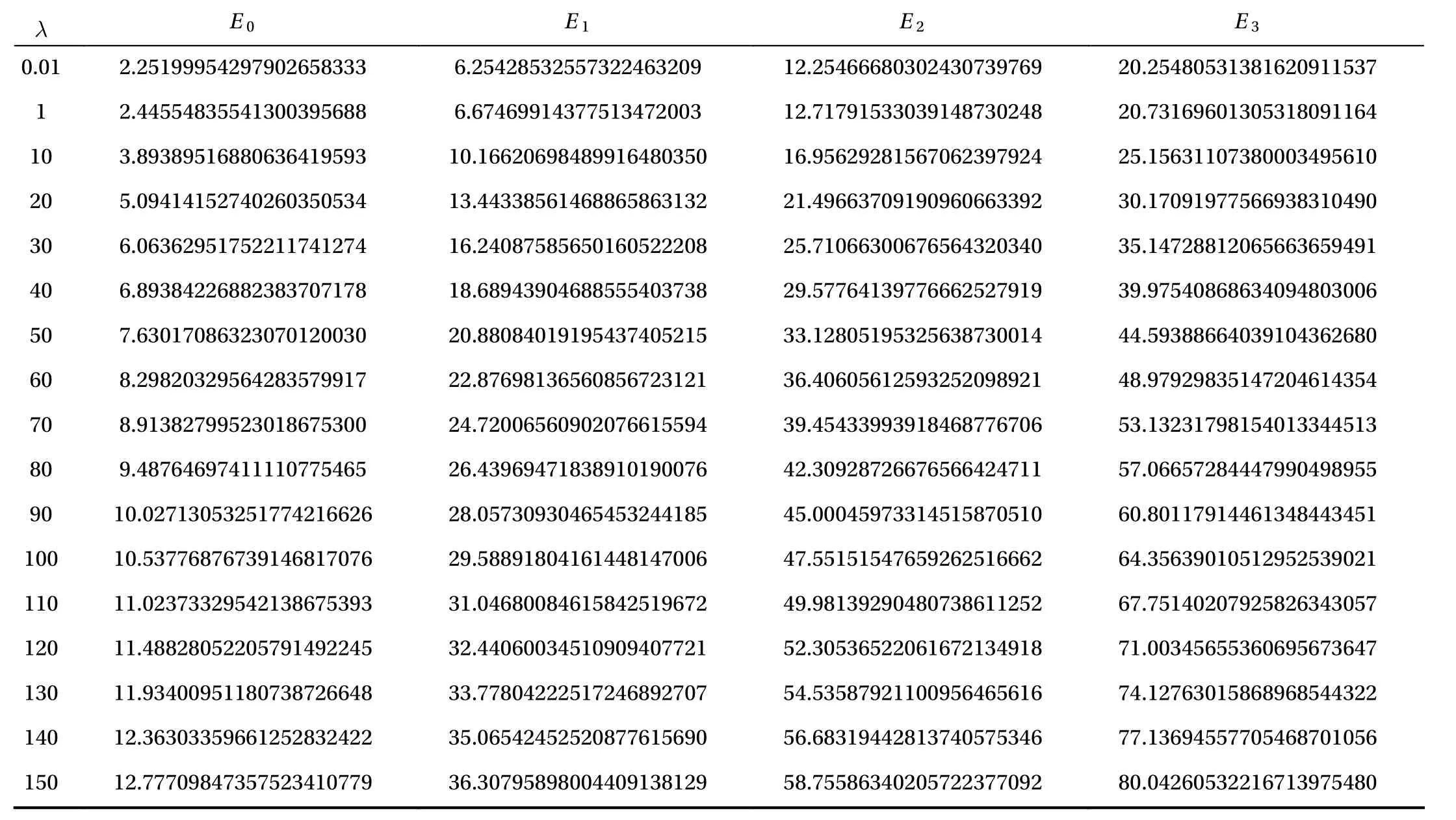
Table 5 The convergent results of eigenvalues and of Eq. (19) at = 0.5 for different values of by means of the HAM-based approach using and the appropriate values of.

Table 6 The convergent results of eigenvalues and of Eq. (19) at = 2 for different values of by means of the HAM-based approach using and the appropriate values of.

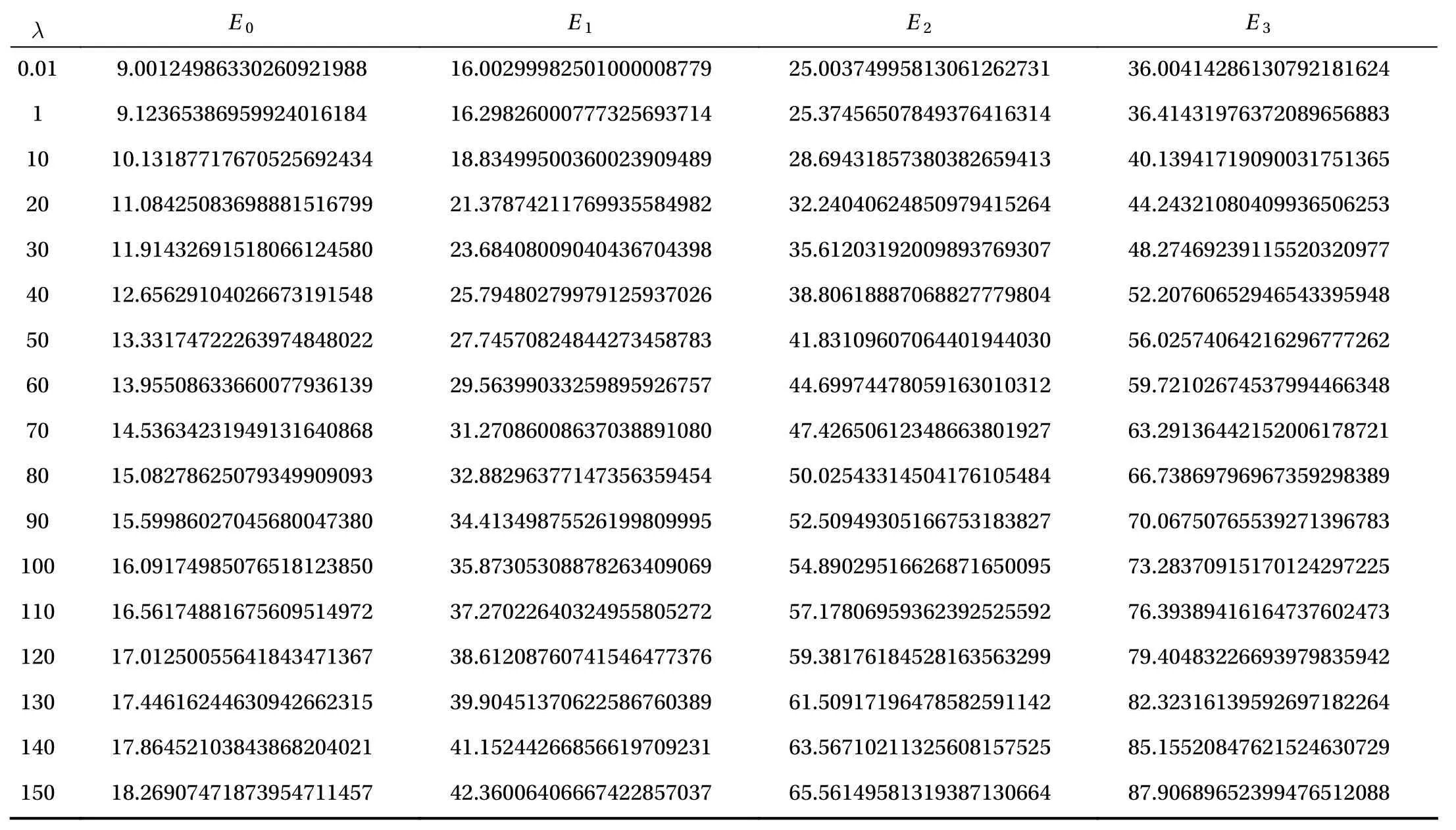
Table 6 The convergent results of eigenvalues and of Eq. (19) at = 2 for different values of by means of the HAM-based approach using and the appropriate values of.

with an orthonormal basis satisfying Eq. (2), whereis the Gegenbauer polynomial,N is a sufficiently large positive integer, l = a +1 and

The eigenvalue Enand its corresponding eigenfunctions ψn(x) for different values of a and n = 0,1,2 and 3 are evaluated using the HAM-based approach given by Liao [18] at small as well as very large disturbances. First, let us consider the eigenvalue E0at a = 0. It is very clear from Table 3 that for high disturbances such as λ = 18 and 20, the residual error square of perturbation series enlarges significantly as the order of approximation increases so that the perturbative results become invalid due to the divergence. The same is reported for higher disturbances. However, even with very high disturbances, the HAMbased approach successfully provides the convergent and accurate results for E0which agree well with the numerical results obtained by a constant reference potential perturbation method(CPM) [20] (see Fig. 2 and Table 4). The same is also noticed for Enand ψn(x) with different values of a. The convergent results of ground state and excited energies En( n = 0,1,2 and 3) in accuracy of 20 digits are listed in Tables 4, 5, and 6 for a = 0,0.5 and 2,respectively. These results also agree well with its homotopy-Padé approximation [10, 12, 18]. This further indicates the general validity of HAM-based approach for the Schrödinger equation in quantum mechanics, and its superiority over the traditional perturbative approaches.

In this article, two examples, i.e. the complex cubic anharmonic oscillator and the perturbed Pöschl-Teller potential, are successfully solved by means of the HAM-based approach first proposed by Liao [18] for the time-independent Schrödinger equations in quantum mechanics. Note that perturbation approach becomes invalid when the disturbance enlarges.However, convergent results of eigenvalue and eigenfunction are always obtained by means of the HAM-based approach, even when the disturbances are quite large, which can be directly compared with the experiment data to improve the accuracy of the experimental findings and/or physical theories. This further illustrates the general validity of the HAM-based approach proposed in Ref. [18] for the time-independent Schrödinger equations in quantum mechanics, and its superiority over the traditional perturbative approaches. This study suggests that the HAM might provide us a new, powerful alternative to solve some complicated problems in quantum mechanics, including manybody problems which we will consider in future.

Acknowledgement

Thanks to the anonymous referees for their valuable comments and discussions. This work is partly supported by the National Natural Science Foundation of China (No. 11432009).