高维Euler方程组的强松驰极限
2019-11-28徐志琳林春进
徐志琳,林春进
(河海大学 理学院,南京 210098)
0 引 言
考虑如下高维带松弛项的Euler方程组:
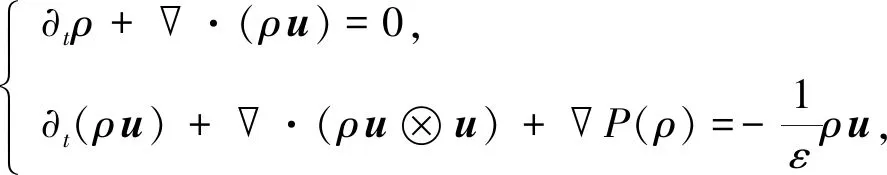
(1)
其初始条件为
ρ(x,0)=ρ0(x),u(x,0)=u0(x).
(2)
这里:x∈n为空间变量;t>0为时间变量;ε>0为松弛常数;ρ(x,t)∈和u∈n分别表示流体在t时刻、x处的密度和速度;P=P(ρ)表示流体的压强,对于任意的ρ>0,满足P′(ρ)>0.
对于Euler方程组整体解的研究目前已有很多成果[1-12]:文献[1]研究了一维Euler方程组在Lagrange坐标下解的大时间行为,并证明了当时间t→∞时,方程组(1)的解收敛于非线性扩散方程的解;文献[5]用流函数的方法证明了等温Euler方程组的解在有界变差的初值条件下收敛于热传导方程的解;文献[6]利用熵变量研究了在初值充分小时,等温Euler方程组的光滑解当ε→0时收敛于热传导方程的解;文献[7]利用熵变量,将文献[6]的结论推广到包含等熵Euler方程组在内的一般Euler方程组上;文献[8]将这类方法推广到一般的松弛极限.但该方法对方程对称子关于变量的依赖关系有较高要求.文献[9]通过引入新的变量,利用Euler方程的等价形式得到了有效的能量估计,从而证明了解的整体存在性;文献[10]在能量估计中利用密度关于时间t的偏导数估计,得到了解的整体存在性;文献[11-12]利用该方法得到了类似的结果.但文献[9-12]中只考虑了带阻尼项的Euler方程解的整体存在性(即ε=1情形),由于缺少关于时间的一致先验估计,因此不能直接用来处理松弛极限.文献[13]讨论了相互作用力下带阻尼的Euler方程的极限模型;文献[14-15]讨论了带阻尼的Euler方程强松弛极限在其他物理模型上的推广.本文借助文献[6-8]的方法和文献[9-10]中能量估计的技巧,建立一般的可压缩Euler方程组的解关于ε的一致先验估计,从而获得光滑解的整体存在性.

这里C和δ与参数ε和初值(ρ0,u0)均无关.
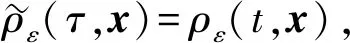


本文关于松弛极限的结论与文献[6]一致,但获得解的估计比文献[6]更精细,且本文对松弛模型的研究方法可推广至更一般的物理模型中.若无特殊说明,本文中C均表示一个与ε和初值均无关的正常数,但不同之处可表示不同的值.用α∈n表示多重指标,即α=(α1,α2,…,αn),其中αi∈,i=1,2,…,n,用|α|表示其阶数,即|α|=α1+α2+…+αn.∂α表示关于x的|α|阶偏导数,‖·‖L2,‖·‖L∞,‖·‖Hk分别表示n上的L2范数、L∞范数和Hk范数.
1 一致先验估计
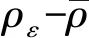

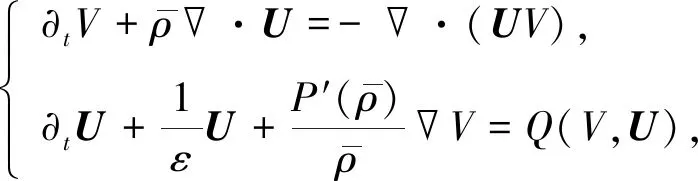
(3)
其中

(4)
由式(3)中的质量守恒方程可得速度变量的散度为

(5)
对于(V,U)∈C([0,T];Hk(n)),定义能量泛函为
若Nε(T)≤δ,则根据Nε(T)的定义以及Sobolev嵌入定理,可知

(7)
由式(7)式,易见

(8)
下面进行能量估计,首先证明如下的L∞(Hk)估计:
命题1若扰动方程组(3)的解(V,U)∈C([0,T],Hk(n)),且满足Nε(T)≤δ,则存在常数C,使得对于∀t∈[0,T],有

下面估计式(10)右端的第一个积分,结合式(5),有
其中[,]表示交换子,即
[A,B]C=A(BC)-B(AC).
对于I1,通过分部积分,有
由式(7)知

则
妇科护理当中安全隐患的出现首相我们应该想到的问题就是关于护理人员的问题,在大多数的妇科护理人员当中他们的法律意识相对来说是较为薄弱的,他们对于法律法规的了解都是十分欠缺的,所以他们对于风险的预知能力是不足的。这样一来也就导致护理人员在护理工作当中不能意识到法律的重要性,缺乏护理的责任心,认为工作疏忽不会给患者带来多大的影响。

(13)
此外,对式(12)右侧第二项分|α|=0和|α|>0进行讨论:当|α|=0时,有
‖V‖L∞≤C‖V‖Hk-1,
根据式(7)并结合Hölder不等式及带ε的Young不等式,有
当|α|>0时,式(12)右侧第二项的估计更简单,则有
把式(13)~(15)代入式(12),可得
对于I2,利用交换子的Moser类估计,并参考文献[16],可得
由复合函数的Moser类估计,并参考文献[16],有
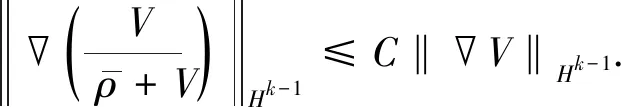
(18)
利用式(17),(18)及Sobolev嵌入不等式,有

(19)
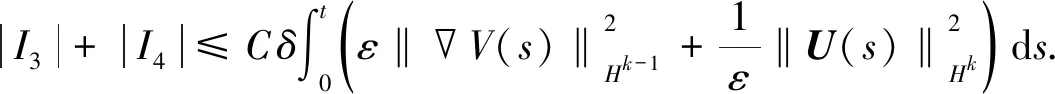
(20)
根据上述估计技巧,I5和I6的估计较容易,有
由估计式(16)~(22),可得
下面估计式(10)右端第二个积分,首先利用表达式,可写为
与前面的估计类似,利用分部积分,J1可化为
对于式(25)右侧第一项,根据式(8)及Hölder不等式易得到估计.对于式(25)右侧第二项,利用式(5),与式(11)中前四项的估计方法类似,有
同理,对J2,J3,J4的估计,有
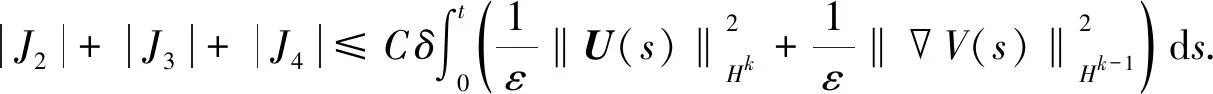
(27)
由式(26),(27),可得
将式(23),(28)代入式(10),当δ充分小时关于|α|≤k求和,即得命题1.
下面讨论Vt的估计.
命题2在命题1的条件下,有
证明: 首先,对式(3)的第一个方程两边同时关于t求导,对式(3)第二个方程两边同时求散度,再将两式相加,并消去(·U)t,得
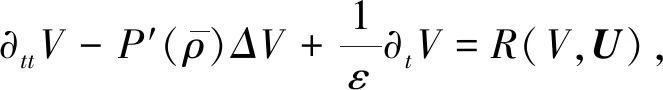
(29)
这里

(30)
然后,对式(29)两边同时关于x求α阶导,|α|≤k-1,再乘以∂α(εV+Vt),并在n×[0,t]上积分,可得
下面估计式(31)右端含有∂αR(V,U)的积分项,利用式(30),把ε∂αR(V,U)∂αV的积分拆成四项:
其中:
与式(24)中的估计类似,I1,I2和I4可估计为
对于I3,利用式(3)的第二个方程,将∂tU用U,V和Q(V,U)表示,I3可分解为
与I1,I2和I4的估计同理,利用分部积分与交换子的性质,I3可进一步估计为

(35)
结合式(32)~(35),可得
式(31)右端积分项中的∂αR(V,U)∂αVt的积分的估计式(36)类似,于是
将式(36),(37)代入式(31),当δ充分小时,关于|α|≤k-1求和,即得命题2的估计.
根据一致先验估计,并由质量守恒可知:Vt(0)=-·[(V0+1)U0],从而可得解的一致先验估计,进而获得解的整体存在性[6,9].
