协作机器人SHIR5动力学建模及固有频率分析与优化*

田 勇，王洪光，潘新安，胡明伟

(1. 中国科学院 沈阳自动化研究所，沈阳 110016；2. 中国科学院 机器人与智能制造创新研究院，沈阳 110016；3. 中国科学院大学，北京 100049)

0 引言

随着机器人的广泛应用，对机器人的需求由大型、负载自重比小的传统工业机器人向轻型、负载自重比大的协作机器人方向发展。协作机器人是指能够在指定的协作区域内与人进行直接交互的机器人[1-2]。协作机器人具有轻型、负载自重比大的特点，需要协作机器人采用一体化关节和轻质连杆。但是关节和连杆的柔性导致了机器人的刚度降低，导致机器人在运行过程中容易出现低频谐振，且到达目标位置时出现残余振动，降低机器人的精度。为了保证机器人能够高速平稳运行，就需要对柔性机器人的动态特性进行分析研究[3-4]。

目前，针对机器人柔性的研究，主要分为对柔性连杆和柔性关节的研究。对于柔性关节的研究中，黎田[5]考虑了关节柔性建立了机器人的动力学模型，并且通过主动抑振的方法对机器人进行了振动抑制； Korayem等[6]通过分析关节柔性对承载能力的影响，指出关节柔性的增加会降低机械臂系统的最大承载能力；Korayem等[7]考虑关节和连杆的柔性，对移动操作臂进行了动力学模型进行了分析，并研究轨迹对柔性操作臂的影响，证明提出方法的有效性。针对于连杆柔性，Lee[8]通过假设模态法建立了柔性杆的柔性变形，研究了带有末端质量的柔性杆的振动特性；Low[9]利用有限元法建立了柔性杆的有限元模型，并研究了末端负载对柔性杆动态特性的影响；高胜等[10]通过有限元方法建立了柔性机器人的动力学模型，研究了连杆参数对动态特性的影响；Farid[11]通过拉格朗日法和有限元法对含有关节和连杆柔性的冗余机器人进行了动力学建模，并通过数值法预测系统的动态行为。文献[12-15]研究了关节及连杆的柔性对机器人动态特性的影响，大多针对单连杆或平面机器人进行分析。

协作机器人SHIR5是7DOF冗余机器人，本文利用有限元法和拉格朗日法建立了机器人SHIR5的刚柔耦合动力学模型，并考虑机器人的关节和连杆的柔性，提高了机器人动力学模型的准确度。然后研究了机器人各参数对其固有频率的影响，为后续的结构设计提供了有力的支撑。最后利用遗传算法对机器人参数进行了优化，提升了机器人的固有频率。

1 机器人模型及简化

图1 机器人三维模型及等效模型

图1所示为SHIR5机器人的三维模型及等效模型。可以看出，机器人的连杆为不规则形状。首先对连杆进行简化，将连杆分为两部分：圆形薄壁部分和非圆形薄壁部分。定义圆形截面的直径为D，椭圆形截面的长短轴分别为D、B，连杆的厚度为d。

由表1可以看出，关节的倾覆刚度远远大于关节的扭转刚度。因此，通过线性扭簧对关节进行简化。如图1所示，θ为电机转角，关节的刚度为k，关节的弹性变形为φ。

表1 对关节简化后的参数设置

通过连杆和关节的简化，得到机器人的整体简化模型，如图2所示。将连杆简化为圆形截面和椭圆截面的两个单元，设连杆Li上的单元j的序号为ij，单元的长度及单位长度质量分别为lij、mij。关节Ji质量为mpi，扭转刚度为ki。连杆L7及关节J7对系统的影响较小，为简化模型，将L7等效为刚性连杆，将关节J7等效为集中质量，P为负载。

图2 机器人的等效模型

根据材料力学的知识，可以得到连杆的参数与连杆的D、B、d有关，如连杆的抗拉刚度、抗弯刚度、抗扭刚度以及单元长度质量参数。

2 有限元模型的建立及动力学推导

2.1 机器人的运动关系描述

对于柔性连杆的建模，主要有有限元法和假设模态法[16]。本文中的连杆截面较为复杂，因此采用有限元法对柔性连杆进行建模[17]。本文采用空间梁单元对机器人进行建模，得到机器人的柔性运动关系，如图3所示。

图3 机器人柔性运动关系

首先建立系统坐标系O-x0y0z0，以及随连杆运动的局部坐标系O-xiyizi，局部坐标系的zi轴始终与连杆i重合。其中关节的理论转角为θi，关节的弹性变形为φi；在局部坐标系中，连杆i含有两个单元，单元的变形位移和变形转角分别为uij(z,t)、vij(z,t)，其中i代表连杆序号，i=1, 2,…, 6；j代表单元序号，j=1, 2。

连杆i上任意一点在局部坐标系中的位置为ri′， 当位于连杆的单元j=1时，ri′=[z+ui1(1,1);ui1(2,1);ui1(3,1); 1]；当位于连杆的单元j=2时，ri′=[li1+z+ui2(1,1);ui2(2,1);ui2(3,1); 1]，则ri′的表达式为：

(1)

其中，li1为单元1的长度，i=1, 2,…, 6；j=1, 2。

柔性杆在系统坐标系中的转换矩阵通过前一连杆和前一关节的变换矩阵进行转换，其中关节的转动变换矩阵为T1，关节的柔性变形的变换矩阵为T2，连杆的变换矩阵为T3。则柔性杆i上任意一点在系统坐标系中的位置表示为：

ri=T13·T11·T12·…·Ti3·Ti1·Ti2·ri′

(2)

2.2 动力学模型的推导

机器人的动能包括连杆的动能，集中质量的动能以及关节的动能。势能包括连杆的弹性势能、连杆及集中质量的重力势能以及关节的弹性势能。

(3)

(4)

(5)

通过公式可以得到系统的总动能及势能，并利用拉格朗日方程，得到系统的动力学方程及固有频率方程：

(6)

(7)

其中,M为系统的质量矩阵，H为系统的科氏力、离心力，K为系统的刚度矩阵，G为系统的重力。

3 连杆参数对固有频率的影响

固有频率与连杆的长度Li、连杆圆形截面长度li1、连杆厚度di、连杆直径Di、短轴Bi、关节质量及刚度有关。上述参数对固有频率的影响如图4所示。

(1)d1、d4和d5对固有频率影响很小，且随d1、d4的增加，固有频率略有提高，而随d5的增加，固有频率略有降低。随d2、d3的增加，固有频率随之增加，但d2比d3的影响大；随d6的增加，固有频率随之降低。

(2)随着L2、L3、L4的增加，机器人的固有频率随之增加，L2的影响比L3、L4大；随着L5、L6的增加，机器人的固有频率随之降低，因此，在连杆长度设计过程中，应该增加L2、L3、L4的长度，并对其进行优化设计。

(3)各连杆的比例系数ll对固有频率的影响中，ll4、ll5、ll6越大，机器人的固有频率就越低，且ll6的影响最大；ll2、ll3对固有频率影响较小，随着ll2、ll3的增大，固有频率略有升高，因此在连杆的设计过程中，适当减小ll4、ll5、ll6，增大ll2、ll3。

(4)B3对固有频率的影响最大，相比于其他连杆截面来说，对固有频率的灵敏度最高；随着B2、B3、B4、B5的增加，机器人的固有频率随之增加，且最终会稳定在一定的范围内;随着B6的增加，机器人固有频率先增大后减小，因此设计过程中该参数有最优值。

(5)随着D2、D3、D4的增加，机器人的固有频率随之增加，且D3对固有频率的影响最大；随着D5的增加，机器人的固有频率先增加后减小，对固有频率的影响较小，再设计过程中有最优值的选择；随着D6的增加，机器人的固有频率减小，因此在设计过程中尽量减小该值。

(6)在其他参数不变的情况下，随着机器人末端负载的增加，机器人的固有频率随之降低。

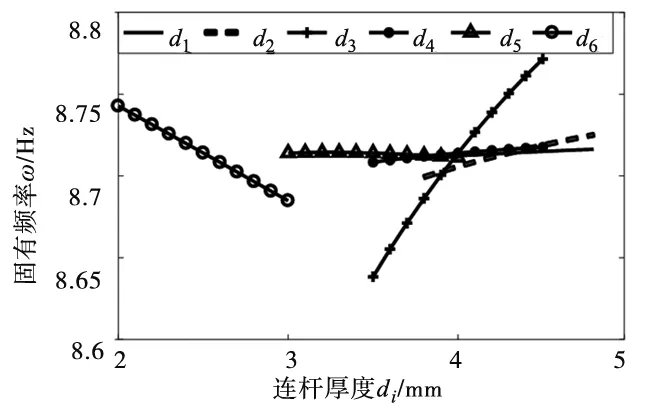
(a) 连杆厚度对固有频率的影响

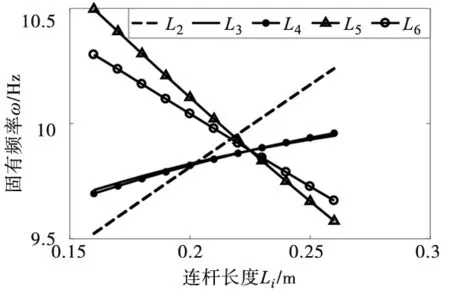
(b) 连杆长度对固有频率的影响

(c) 截面比例对固有频率的影响

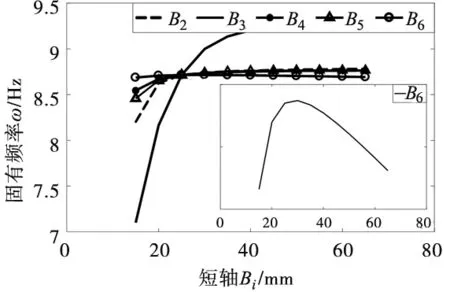
(d) 短轴对固有频率的影响

(e) 长轴对固有频率的影响

(f) 负载对固有频率的影响 图4 各参数对固有频率的影响

4 设计参数的优化设计

通过上节可以看出，机器人各连杆和关节参数对机器人的固有频率影响较大。其中，关节的质量和刚度很难提升和改变，因此在设计过程中保持关节的质量和刚度不变，对机器人的连杆参数进行优化设计。

针对机器人连杆参数的优化，分析发现部分连杆参数对固有频率的影响较大，如d2、d3，L3、L4、L5、L6，ll2、ll3，B3以及D2、D3、D4。通过对上述参数进行优化设计，对应的参数如表2所示。首先，建立优化参数与固有频率的数学模型：

ω=f(L3、L4、L5、L6、ll2、ll3、ll4、D1、D2、B3、d2、d3)

f表示固有频率与机器人连杆参数的数学模型，本文通过Kriging方法进行拟合。

各变量的取值范围为：

L3∈[0.2, 0.35]；L4∈[0.2, 0.35]

L5∈[0.14, 0.25]；L6∈[0.14, 0.25]

ll2∈[0.3, 0.7]；ll3∈[0.3, 0.7]；ll4∈[0.3, 0.7]

D1∈[100, 200]；D2∈[100, 200]

B3∈[40, 80]；d2∈[3.5, 5]；d3∈[3.5, 5]

优化过程中保证机器人的总质量m和总长度L保持不变，约束条件为：L=0.9m；m=5kg，且

L3+L4+L5+L6=1

其中，机器人的总质量的计算公式为：

(8)

m=m1+m2

m1，m2分别为圆形截面、椭圆形截面的质量。

利用遗传算法对模型进行优化，得到的优化结果如表3所示。通过对比可以看出，通过对连杆参数的优化，在保证机器人质量和总长度不变的情况下，机器人的固有频率由原来的9.687Hz提升到10.562Hz，提升了9%，说明了优化的有效性。

表2 优化参数设置

表3 优化前后固有频率对比

5 结论

柔性关节和柔性连杆的引入导致了协作机器人的动态特性降低。本文通过有限元法对机器人SHIR5的柔性连杆进行了建模，并利用拉格朗日法建立了机器人的动力学模型；通过动力学模型求解机器人固有频率以及机器人参数对固有频率的影响，为机器人的设计提供了理论基础；利用分析得到对固有频率影响较大的参数，通过遗传算法对该参数进行了优化，在保证机器人质量不变的前提下，使得机器人的固有频率提高了9%，说明了优化的有效性。