基于雅可比旋量的并联配合特征三维公差分析方法及其应用
2019-11-27李刚炎王平俊刘思睿
熊 峰,李刚炎,王平俊,刘思睿
(武汉理工大学 机电工程学院,武汉 430070)
0 引言
机械产品在装配过程中,零件误差会积累形成装配误差,从而影响产品的性能。随着机械制造精度以及对产品性能要求的提高,产品的公差分析已经成为提升产品性能的重要方法之一。对于传统的以二维为基础,通过传统的尺寸链计算分析方法进行设计的线性尺寸公差分析已经不能适应现代产品设计的要求,公差分析逐渐转变为以三维为基础的复杂产品的装配公差分析,同时公差分析的精度也不断提高。三维公差分析方法是通过描述刚体的某些特征在三维空间的公差域变动,和装配体各零部件之间的装配关系与结合面特征,来表示装配体的三维装配公差。
目前,对于三维公差分析,国内外相关领域学者已经提出了诸多分析方法,基于三维几何的公差分析模型主要有:文献[1]采用小位移旋量分析装配中的结合面误差,提出JSS矩阵方法,分析装配误差分量的传递路径,结合雅可比矩阵,建立了齿轮泵装配误差模型,验证该方法准确性;文献[2]运用小位移旋量表达几何要素在公差域内的变动,结合齐次坐标变换传递装配误差,并计算封闭环的相对于全局坐标系的变动,根据实例分析,验证了该方法的可行性;文献[3]分析了多种二维和三维公差分析方法,结合实例描述了各方法的特点,总结了三维公差分析方法的优势;文献[4]以齿轮泵体为例,运用雅可比旋量建立了装配体公差数学模型,分析实际工况对产品性能及公差设计的影响;文献[5]介绍了三维公差分析方法T-Map,并结合该方法进行实例分析,验证了该方法的实用性;文献[6]比较了现有的多种三维公差分析方法,结合实例分析,对比了各方法的分析结果;文献[7]运用雅可比旋量建立某装配体的装配公差模型,并对其进行了公差的优化分配。
上述研究提出的三维公差分析方法可较好的解决装配中的误差分析问题,但对于多配合面误差传递则无法准确表达。本文针对常见的多配合面装配关系,结合雅可比旋量模型将尺寸公差与形位公差统一于一个装配模型中,建立了并联配合特征的旋量表达,分析并联配合特征在多配合面装配关系中对装配误差的影响,并以某型三缸发动机平衡轴系统配重块为例进行三维装配公差分析。
1 装配公差分析中的雅可比旋量模型
雅可比旋量模型是擅长公差传递的雅可比矩阵和擅长三维公差表达的旋量模型的结合。雅可比矩阵最早用于机器人领域,随后被引入公差分析领域中,是将公差域的变动假想为机器人关节的运动,运用雅可比矩阵传递装配体的装配误差。在雅可比矩阵中,一般将装配体中的各项公差分为功能要求副(functional requirement,FR)和功能单元副(functional element,FE)。功能要求副即为装配体中的关键值,如封闭环数值。FE指各参与装配零部件的相关公差,一般根据其是否属于参与配合的结合面分为内部功能单元副(internal FE,IFE)和接触功能单元副(contact FE,CFE)。
旋量法也称小位移旋量法,是一种运用运动旋量来表达公差变动域的公差分析方法[8],α、β、γ分别表示绕x、y、z轴旋转的微小变动量,u、v、w分别表示沿x、y、z轴平动的微小变动量,通过这6个矢量的变化,表示刚体的几何特征在三维空间中的微小变动,见图1。
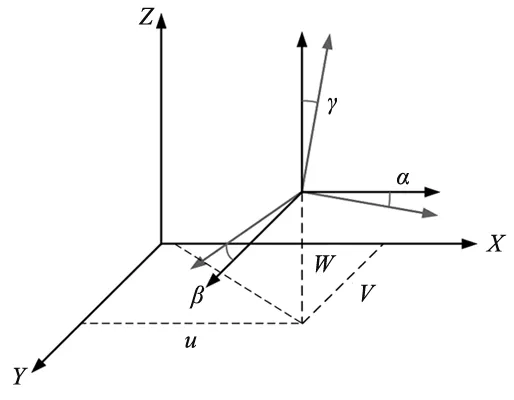
图1 空间变动量示意图
雅可比旋量结合雅可比矩阵法与旋量法,用于公差分析的传递模型可表达为:
(1)
其中,[JFEi]表示各关节对应的雅可比矩阵,其数学表达式为:
(2)

2 装配并联配合特征及其三维公差表达
2.1 典型配合特征三维公差的旋量表达
常见的产品装配中,配合特征多为平面配合或轴孔之间的配合,即平面特征与柱面特征,如图2所示。

(a) 平面特征 (b) 柱面特征 图2 典型配合特征
2.1.1 装配中的平面特征

2.1.2 装配中的柱面特征
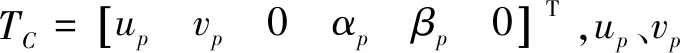
2.2 机械装配中的并联配合特征
现代复杂产品的装配中,装配结合面之间一般会有多个参与装配的特征,将这样的结构称为并联配合结构。具有多个配合特征的配合结构将会传递多个配合特征,包含多个配合特征信息,因此该配合特征不能简单地用一个对结合面的配合来描述。在雅可比旋量模型中,对于这种配合结构,往往会做简化处理,则只能描述其中某一特征,而忽略其中的一部分公差信息,在公差累积中,导致模型建立出现偏差,计算结果不能表达完整的装配公差信息。并联配合特征见图3。
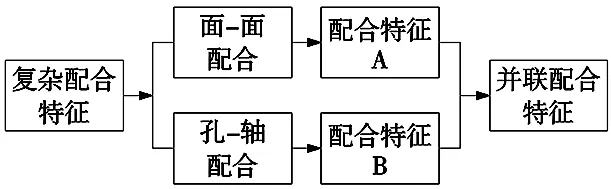
图3 并联配合特征
一个并联组合配合结构常包含多个配合特征,多个配合特征之间相互影响,使得并联组合配合结构的误差旋量表达较为复杂。分析并联组合配合结构的实际误差旋量表达时,应充分考虑各配合特征间的相互作用对组合配合面误差旋量表达的影响,从而获得各并联配合特征的实际误差旋量。若不同配合特征误差旋量的交集不为空,则表示这些配合特征在某误差分量方向上存在重复的约束作用。对于可传递同一误差分量的不同配合特征而言,当其中一个配合特征完成了该误差分量方向上的装配后,其他配合特征在该方向上的装配将受到影响,导致原有的误差旋量发生改变。
2.3 机械装配并联配合特征三维公差表达
如图4包含了两组配合特征,即轴-孔间隙配合和两端面的配合,称为并联配合特征。轴-孔间隙配合具有4个自由度,即沿x、y轴的小位移移动up,vp和绕x、y轴的小位移转动αp、βp,平面贴合具有3个自由度,分别为沿z轴的小位移移动wc和绕x、y轴的小位移转动αc、βc。
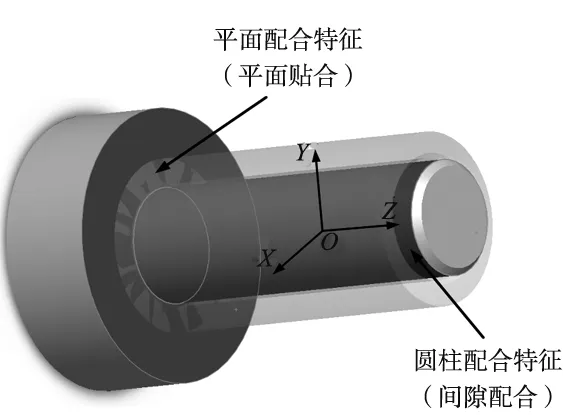
图4 并联配合特征
轴-孔间隙配合的小位移移动up,vp和平面贴合的小位移wc是不同方向的约束,因此三者之间没有互相影响。用于表示并联配合特征的新旋量T中的3个位移矢量变动范围即为上述3个矢量的变动域。根据圆柱特征和平面特征的旋量表达式可看出,两特征对于x、y轴小位移转动矢量具有重复约束。如图4所示的并联配合特征,若平面特征的小位移转动大于圆柱特征的小位移转动则装配不会受到影响,反之,装配则不能成功。因此,新旋量转动矢量的变动范围应该为两旋量相应矢量的交集。因此,新旋量中各矢量的变动范围如式(3):
T=[Vu1∪Vu2Vv1∪Vv2Vw1∪Vw2Vα1∪Vα2Vδ1∪Vδ2Vγ1∪Vγ2]T
(3)
3 实例计算
3.1 计算方法
在雅可比旋量模型分析三维公差时,用合适的旋量来表达并联配合特征是公差分析的关键所在。根据以上分析,可得到带并联配合特征的雅克比旋量模型的分析计算流程,如图5所示。
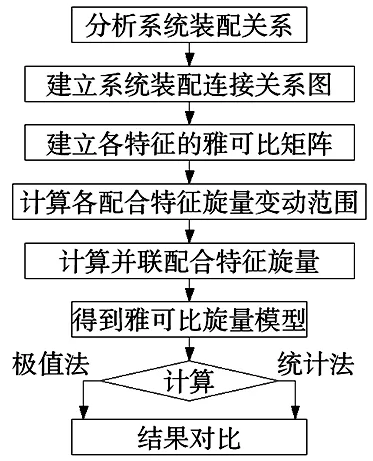
图5 雅可比矩阵模型分析计算流程
图6为某型三缸发动机平衡轴系统,采用单轴平衡机构平衡往复惯性力矩,实现平衡功能的关键是位于平衡轴两端的配重块随平衡轴同步转动,使曲轴旋转产生的不平衡力矩与平衡轴系统产生的不平衡力矩相互抵消。平衡轴系统通过配重形成一个与发动机往复惯性力矩相反的惯性力矩,减小发动机的振动,配重块A、B的装配位姿将对平衡轴系统提供的往复惯性力矩有直接的影响,系统的功能要求(FR)是配重块相对于全局坐标系的公差累积,因此分析配重块的功能要求对平衡轴系统的性能分析至关重要。
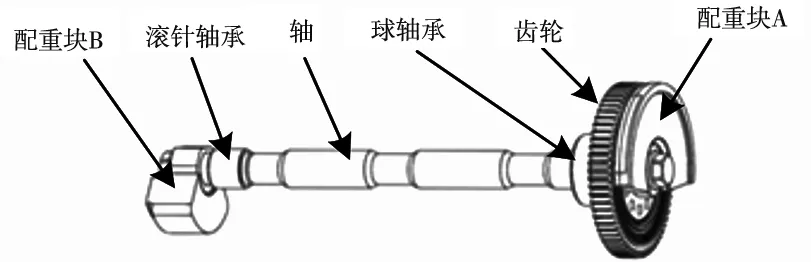
图6 某型三缸发动机平衡轴系统
(1)分析装配关系。某型三缸发动机平衡轴系统包含轴、配重块A、B、轴承、齿轮、端面紧固螺栓等零件,图7所示为轴承、齿轮、配重块A的装配关系,由上分析可知,轴承、齿轮、配重块A、B均在装配过程中与相关部件形成并联配合特征。
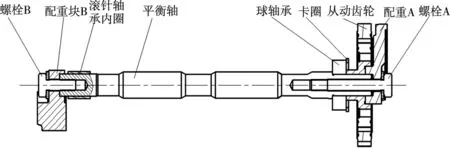
图7 各零部件装配关系图
(2)建立装配连接关系图。如图8所示,图中IFE1表示轴的内部功能特征,CFE1表示轴承与轴平面配合特征,PFE1表示轴承与轴的轴-孔间隙配合特征;CFE2表示轴承与齿轮的平面配合特征,PFE2表示齿轮与轴的轴-孔间隙配合特征;CFE3表示齿轮与配重块A的平面配合特征,PFE3表示配重块A与轴的轴-孔间隙配合特征。
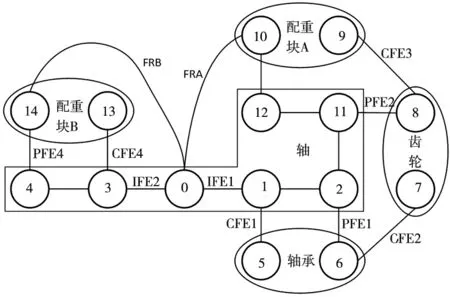
图8 系统装配连接关系图
根据系统的并联配合特征分析,则系统装配连接关系图如图9所示。
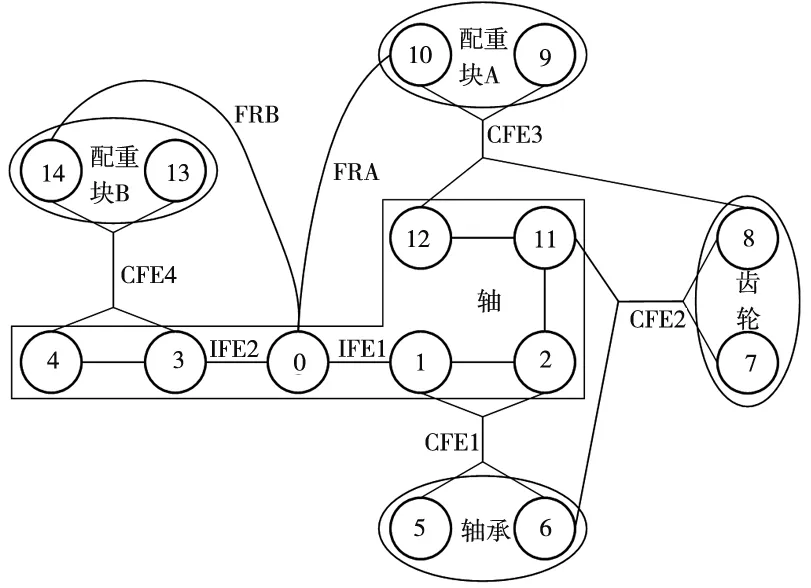
图9 系统并联配合特征装配连接关系图
将原装配连接关系图中的配合特征转化为并联配合特征,并联配合特征CFE1′表示原平面配合特征CFE1与孔轴配合特征PFE1的合成;CFE2′表示原平面配合特征CFE2与孔轴配合特征PFE2的合成;CFE3′表示原平面配合特征CFE3与孔轴配合特征PFE3的合成;CFE4′表示原平面配合特征CFE4与孔轴配合特征PFE4的合成。
则形成传递路径IFE1-CFE1′-CFE2′-CFE3′-FRA,IFE2-CFE4′-FRB。
(3)建立各特征的雅可比矩阵。由式2可得系统中各特征的雅可比矩阵为:
(4)
根据各局部坐标系的空间位置关系,可得dz(IFE1)=40,dz(CFE1′)=34,dz(CFE2′)=12,其余项均为零。
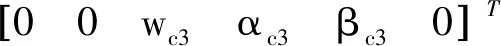
图为与FRA相关的各零件设计公差图,图中信息包含各项尺寸公差与形位公差。

(a) 球轴承 (b) 齿轮 (c) 配重块 图10 零件设计公差图
全局坐标系到轴与定位端面的旋量TIFE1的3个矢量变动范围为:
根据上述分析,轴承、齿轮、配重块A的安装既有平面贴合又有孔轴间隙配合,形成并联配合特征,各并联配合特征的矢量变动范围为:
3.2 验证
(1)采用极值法进行计算验证。FR的6个矢量的公差累积范围。
(2)蒙特卡洛仿真计算验证。蒙特卡洛模拟是一种通过产生大批量的随机数来模拟实际情况的方法,而特征在公差域内的变动也是大批量随机的,因此蒙特卡洛法可以描述公差分析中各旋量的随机变动,见图11。

(a)α模拟分布 (b)β模拟分布 (c)w模拟分布 图11 α、β、w误差统计分布图
通过 Matlab 编程计算,通过生成随机数的方式表达各特征在公差域内的随机变动。进行10000次模拟,得出α、β、w的误差统计分布图,如图12所示。
结果对比。对于只考虑尺寸公差的传统线性尺寸链可运用极值法得到配重块A 的u、v、w尺寸公差。传统的雅可比旋量模型只考虑平面配合特征公差传递路径,忽略了轴-孔配合特征公差,可得到配重块A的α、β、w极值法和统计法的计算结果。
只考虑线性尺寸公差的线性尺寸链可以得到极值法的计算结果:
{-0.025≤u≤0.025-0.025≤v≤0.025-0.82≤w≤0.7}
简化并联配合特征的雅可比旋量模型极值法计算结果:
{-1.4885≤u≤1.3689-0.201≤α≤0.201
-0.201≤β≤0.201}
从表1可以看出,在实际装配中由于形位公差的存在,轴孔之间的实际接触位置具有不确定性,运用雅可比旋量模型计算出的变化范围比尺寸链极值法的范围更大,相对于尺寸链极值法来说更真实反映了装配的不确定性。而对并联配合特征作了简化的传统雅可比旋量法,导致公差分析结果不够准确且缺少部分公差信息。

表1 三种公差分析方法结果对比
4 结论
本文采用雅可比旋量理论进行了三维公差分析,分析了装配体中常见的复杂装配结构。运用基于雅可比旋量模型的并联配合特征三维公差分析方法,建立了考虑尺寸公差与形位公差影响的装配公差三维分析模型。运用蒙特卡罗模拟,在公差域内随机取值,模拟配合面特征的误差变动,进行装配公差累积分析。建立了基于雅可比旋量装配并联配合特征的三缸发动机平衡轴系统配重块装配公差分析模型。根据对比分析可知,所得出的结果比线性尺寸链的分析结果更为全面,比简化的雅可比旋量法分析结果更为准确,更加真实反映了零部件配合面加工的随机性以及零件装配的实际空间位姿情况,更符合工程应用实际。
