表面织构对水润滑轴承混合润滑性能的影响*

(北京理工大学机械与车辆学院 北京100081)

船舶尾轴是船舶动力装置与螺旋桨之间能量传递的重要系统，其中尾轴轴承起着支承螺旋桨尾轴的作用，对轴系能否安全可靠工作起着关键作用。大多数尾轴轴承采用开式水润滑系统，即直接使用海水或河水作为润滑介质。由于水的理化特性不同于矿物质油，其作为润滑介质存在如下问题[1]：水的黏度小、承载力不高，不易形成流体动压润滑，因而容易造成摩擦副间的直接接触；此外水更易发生空化现象，亦会对轴承造成极大的破坏。针对上述问题，HE等[2]建立螺旋桨轴承混合润滑模型，分析了考虑轴的弯曲和不同空化条件下的水润滑轴承性能；KRAKER等[3]建立了水润滑轴承弹流润滑模型，利用有限差分法计算了在一定负载下摩擦副间的接触压力。

表面织构被认为是改善油润滑摩擦副润滑性能的一种有效手段，其原理是表面上的微坑或微沟槽可以充当微流体动压润滑轴承，所产生的附加流体动压力能够有效避免摩擦副表面的直接接触，从而减小摩擦[4]。但将表面织构用于水润滑轴承的研究甚少，目前的相关研究多为全膜润滑情形[5]，缺乏表面织构对水润滑轴承混合润滑性能影响的研究。

为此，本文作者建立了JFO空化边界条件下具有表面织构的水润滑轴承混合润滑模型并数值求解，以获得不同织构参数下的Stribeck曲线，分析不同织构参数对水润滑轴承润滑状态的影响。

1 数学模型

图1所示为文中研究的水润滑滑动轴承，其轴套内表面加工了一系列规则排列的表面织构。由于水的黏度较低，并假设轴承完全沉浸在水中，因此在润滑分析中可以不考虑压力及温度变化对水的黏度和密度的影响。图1中ω为轴颈的旋转角速度，e为偏心距，ε=e/c，ε、c分别为偏心率和半径间隙，y代表轴承轴向方向。

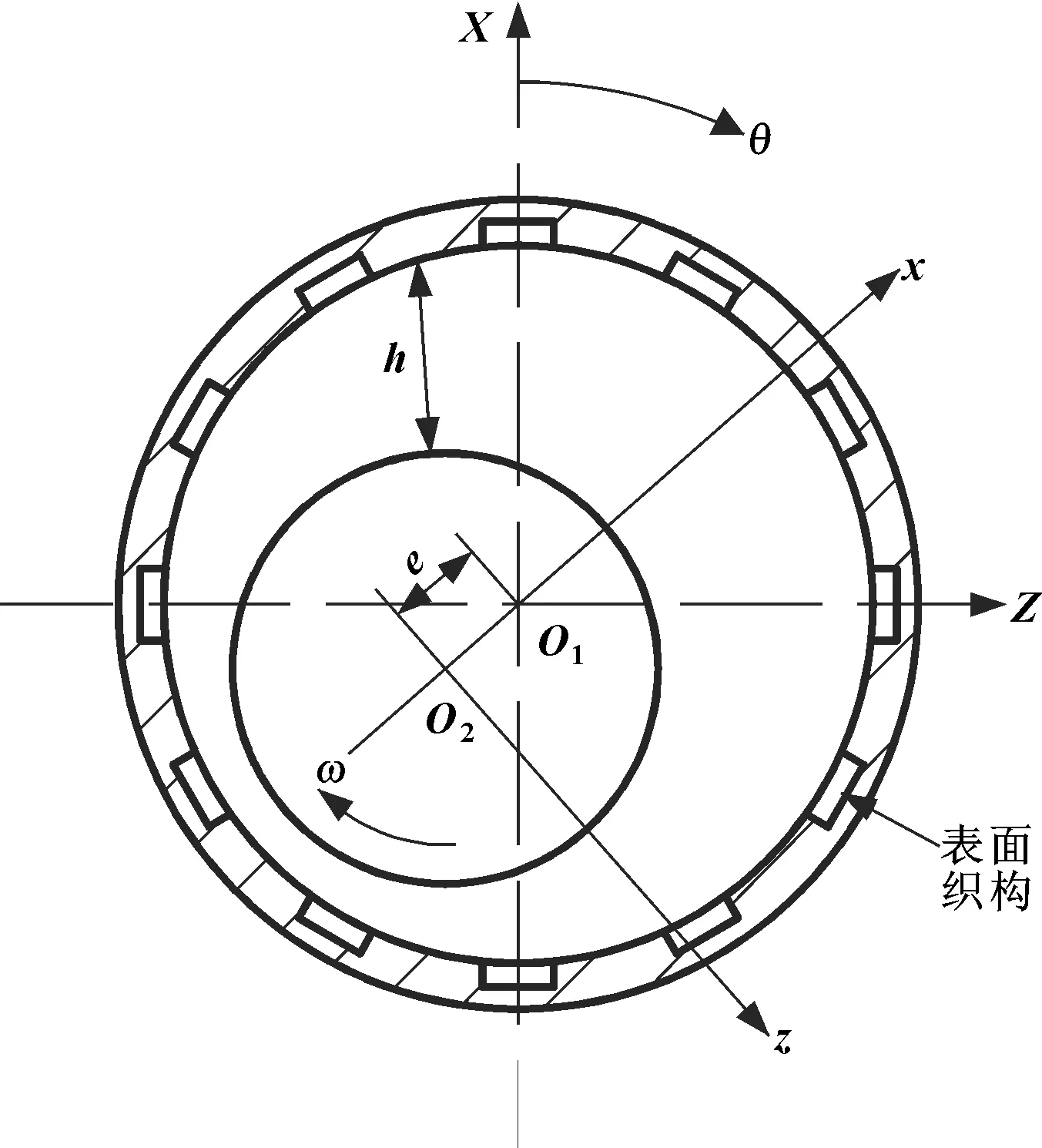
图1 水润滑轴承模型Fig 1 Lubrication model of water lubricated bearing

1.1 膜厚方程

如图1所示，名义水膜厚度h的几何近似关系为

(1)

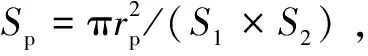
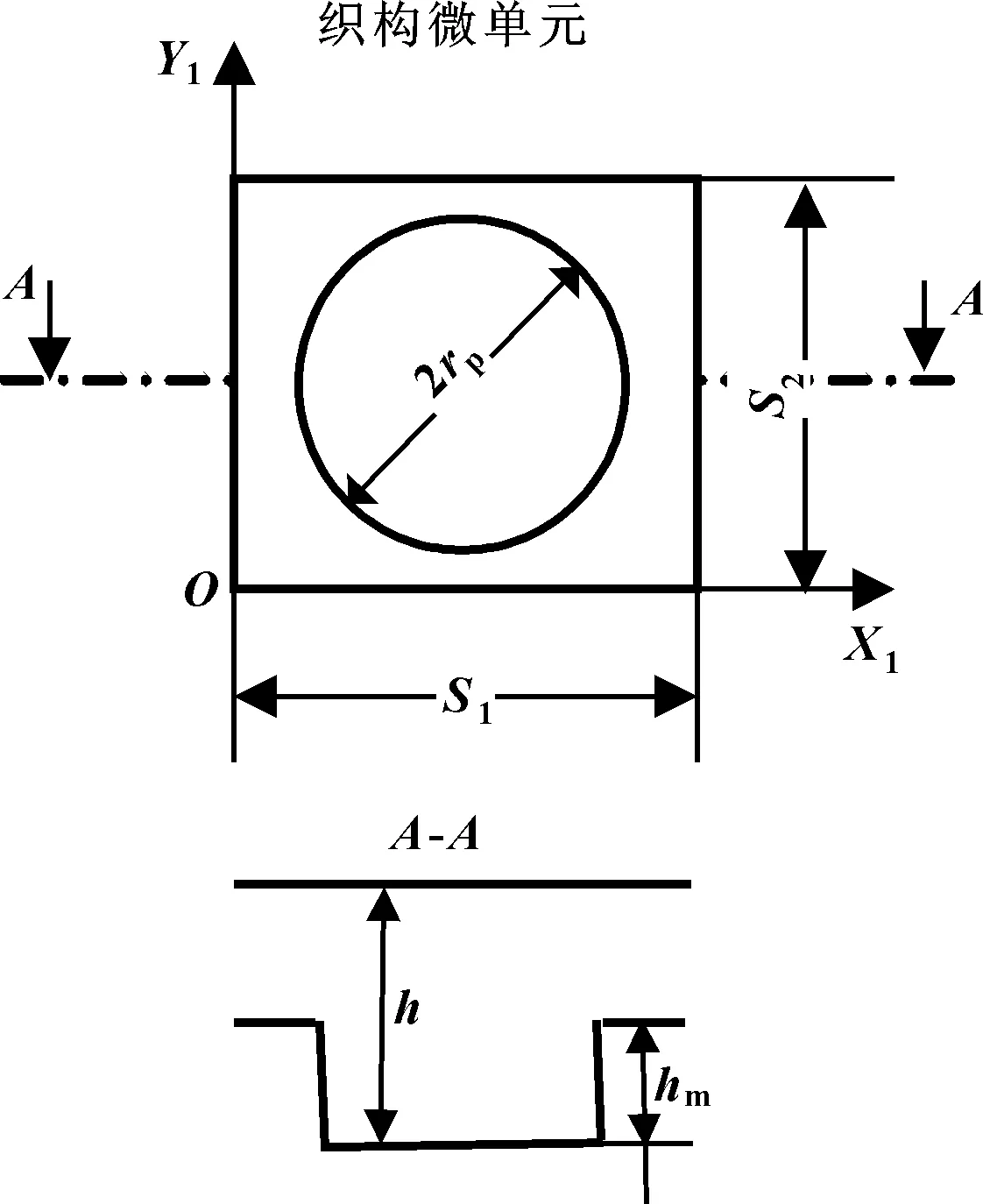
图2 表面织构模型Fig 2 Model of surface texture

1.2 平均流量Reynolds方程

根据文献[6],通过引入变量φ和开关函数F将水膜区和空化区的平均Reynolds方程统一起来，在数值计算过程中自动确定水膜破裂和再形成边界。不同区域内φ的物理含义不同：

(1)在水膜完整区，φ代表量纲一压力，即

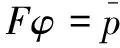
(2)

(2)在水膜破裂区，φ代表空化指数，即

(3)

其中ρ在全膜区时恒等于水的密度ρc，而在空化区时为液-汽两相流的密度。

式(2)、(3)中，F开关函数的定义为

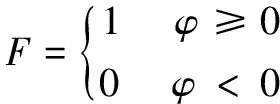
(4)

轴承量纲一化参数如下：

因此，基于JFO空化边界条件并考虑粗糙度影响的平均Reynolds方程量纲一化形式为

(5)

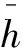
1.3 空化条件和边界条件

JFO空化边界条件为

在水膜的再形成边界上：

求解压力时的边界条件如下：

(6)

式中：p0为环境压力。

1.4 接触模型

轴承表面微凸体在润滑过程中的接触能承担部分载荷，根据BOWDEN和TABOR理论[9]，其接触压力pA计算公式为

(7)

式中：H为轴承材料的硬度。

1.5 承载力和摩擦力的计算公式

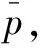
水润滑轴承总的承载力大小为水膜承载力WH与接触力WA之和，即

W=WH+WA

(8)

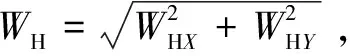
(9)

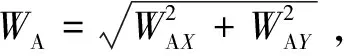
(10)

轴承总的承载力与外部负载平衡，平衡条件为

Fload+W=0

(11)

在混合润滑状态下，摩擦力由流体摩擦力FH和峰元摩擦力FA两项组成，即：

(12)

式中：μf为粗糙峰接触摩擦因数。

因此，摩擦副间摩擦因数为

(13)

2 计算结果与分析

为验证织构模型的正确性，现暂忽略粗糙峰的接触和JFO空化边界条件，将计算结果与文献[10]中的计算结果进行对比。由图3可知，文中计算结果与文献[10]中能够很好地吻合，验证了文中织构模型的正确性。下面将基于该模型及求解方法，研究不同织构深径比及面密度对海水润滑轴承性能的影响。

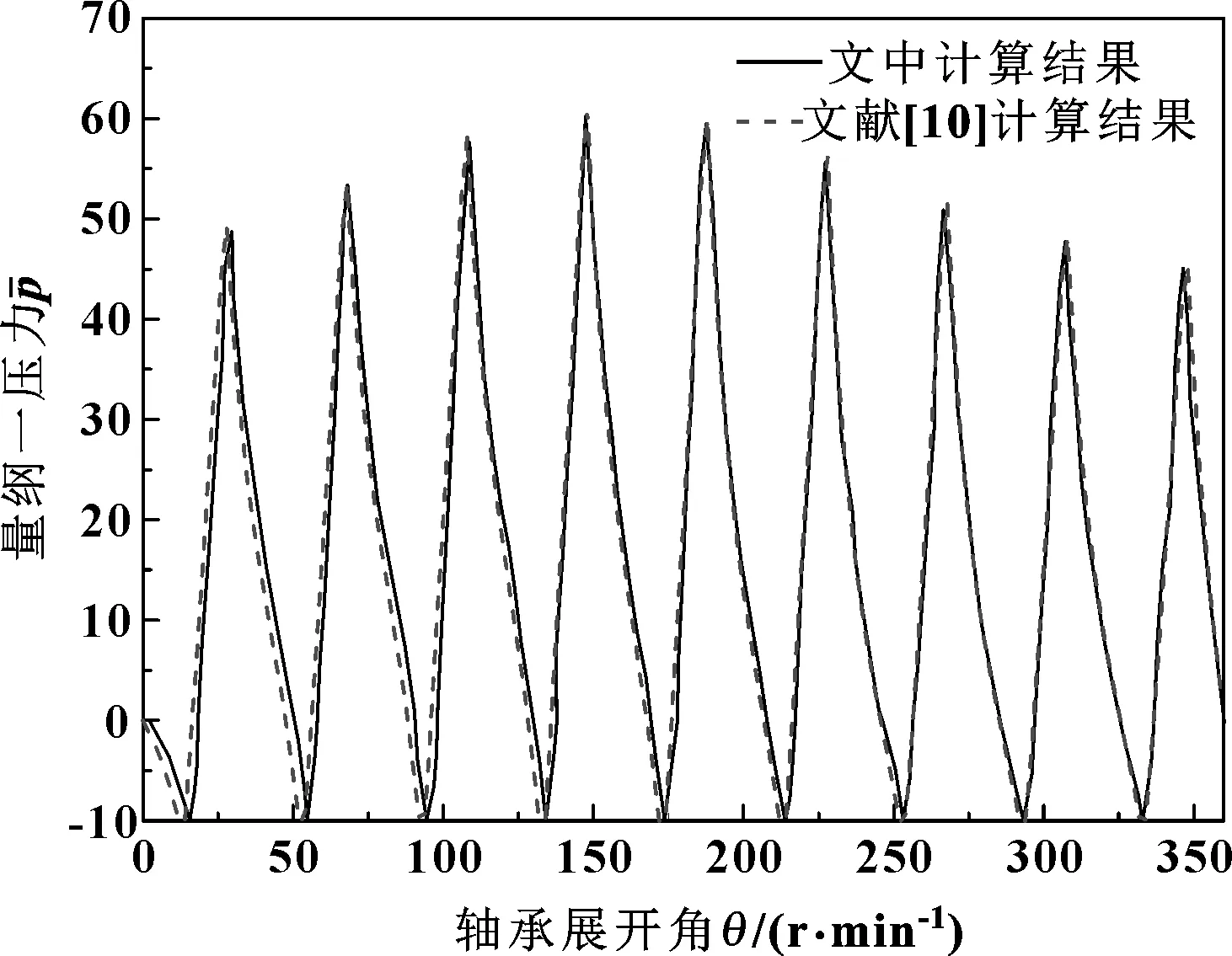
图3 计算结果与文献[10]对比Fig 3 Comparison of calculation results with Ref. [10]

表1给出了计算中所使用的海水润滑轴承参数。

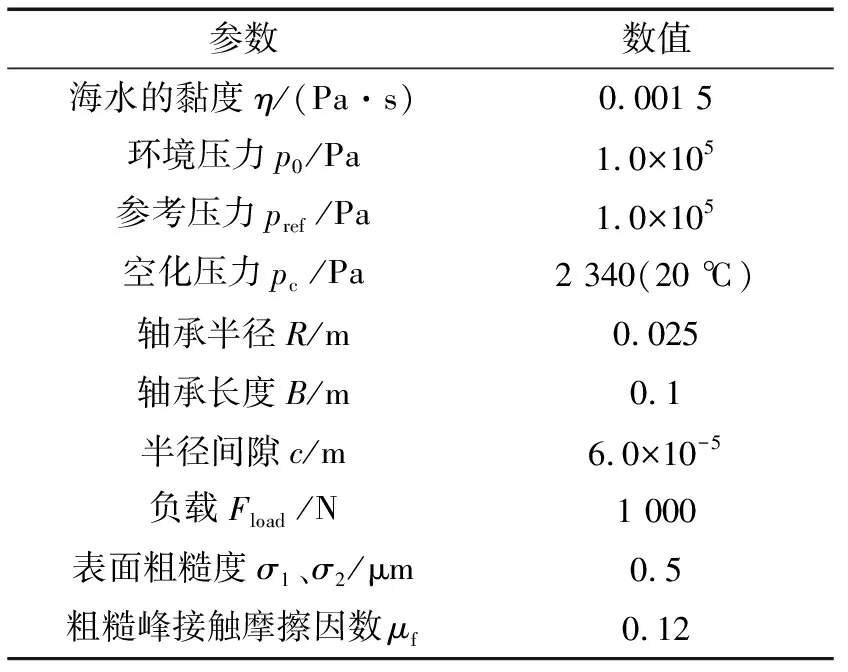
表1 海水润滑轴承参数

2.1 织构深径比对水润滑轴承润滑性能的影响

图4所示为织构半径rp=500 μm时，不同深径比下最小膜厚比随转速的变化曲线。图中h/σ=3的横线代表混合润滑和流体动压润滑的分界线，横线上方代表流体动压润滑，下方代表混合润滑。A、B、C、D 4点分别代表各曲线由混合润滑进入流体动压润滑的转折点。从图4可以看出，当转速相同而织构深径比λ<3%时，轴承间的最小膜厚比随深径比的增加而增大，而当深径比λ=3%时，轴承最小膜厚比无织构时还有所降低。

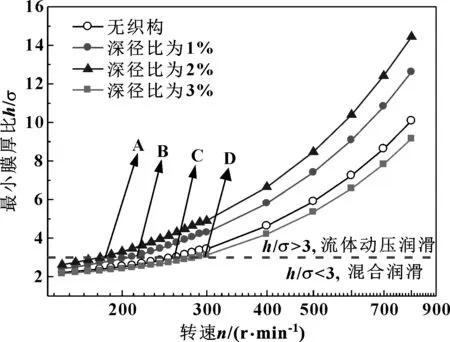
图4 织构深径比对最小膜厚比的影响Fig 4 Effect of texture aspect ratio on minimum film thickness ratio

图5所示为织构半径rp=500 μm时，不同深径比下摩擦因数随转速的变化曲线。可以看出，当转速相同而深径比λ<3%时，摩擦因数随深径比的增加，呈现减小的趋势，深径比λ=2%时摩擦因数最小，并且在最低转速下由混合润滑进入流体动压润滑；但深径比λ=3%时轴承摩擦因数比无织构时还有所增加，且在较高的转速下才能进入流体动压润滑状态。其原因在于：随着深径比的增大，织构内流体动压效应增强，水膜厚度变大，摩擦因数减小；当深径比过大时，由于微凹坑织构内负压的增大，降低了流体动压效应，反而造成了摩擦因数的增加。

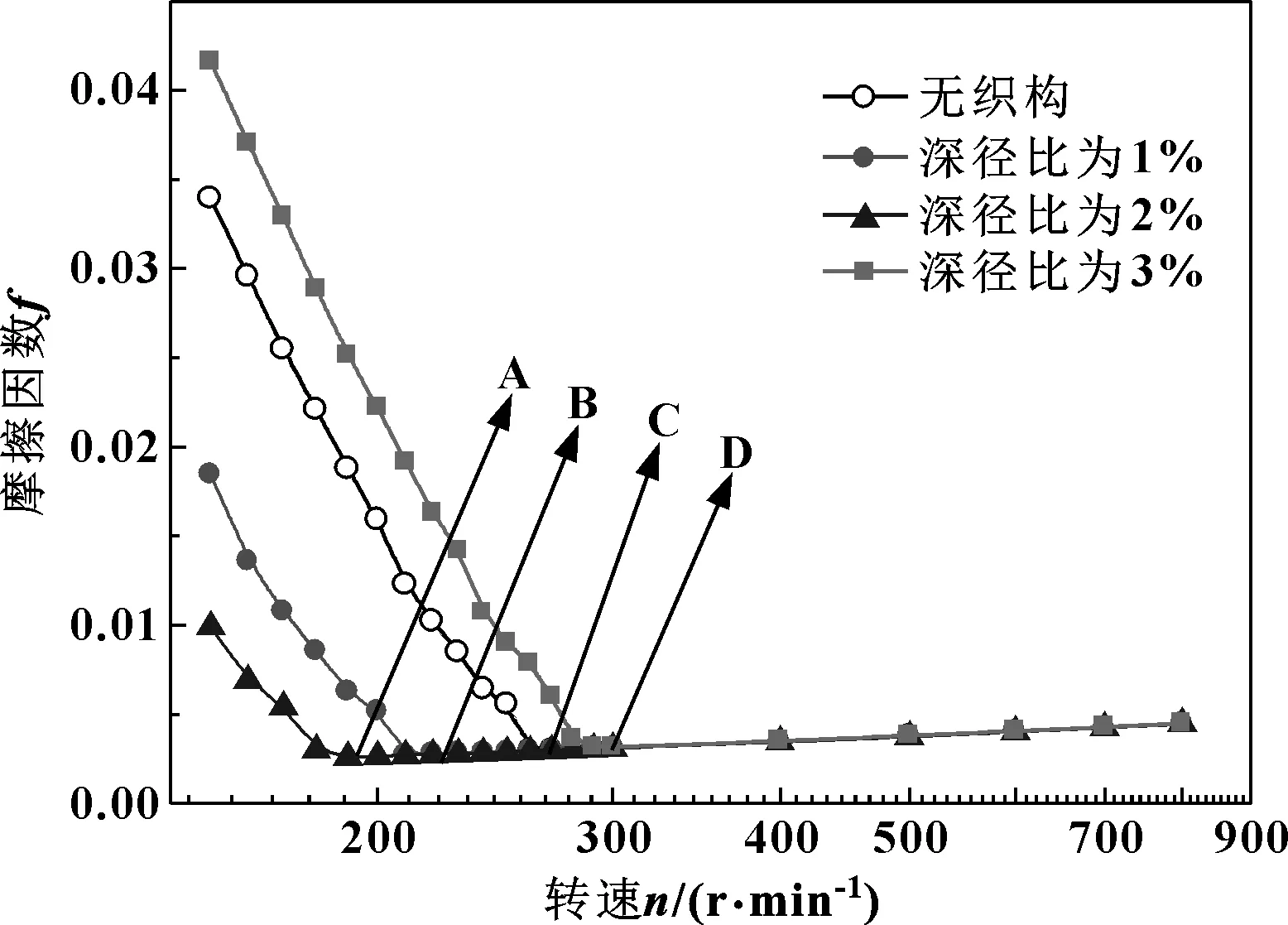
图5 织构深径比对摩擦因数的影响Fig 5 Influence of the ratio of depth to diameter of surface texture on friction coefficient

由此得出：织构深径比是影响水润滑轴承摩擦因数的重要参数之一，深径比在一定范围内能有效降低摩擦因数，增加水膜厚度，使轴承在降低转速下进入流体动压润滑。

2.2 织构面密度对水润滑轴承润滑性能的影响

图6所示为织构深度hp=10 μm时，不同面密度下最小膜厚比随转速的变化曲线。图中h/σ=3的横线代表混合润滑和流体动压润滑的分界线，横线上方代表流体动压润滑，下方代表混合润滑。A、B、C、D 4点分别代表各曲线由混合润滑进入流体动压润滑的转折点。从图6可以看出，在转速相同而面密度Sp<15%时，轴承间的最小膜厚比随着面密度的增加而增大，而当面密度Sp=15%时，轴承最小膜厚比无织构时还有所降低。

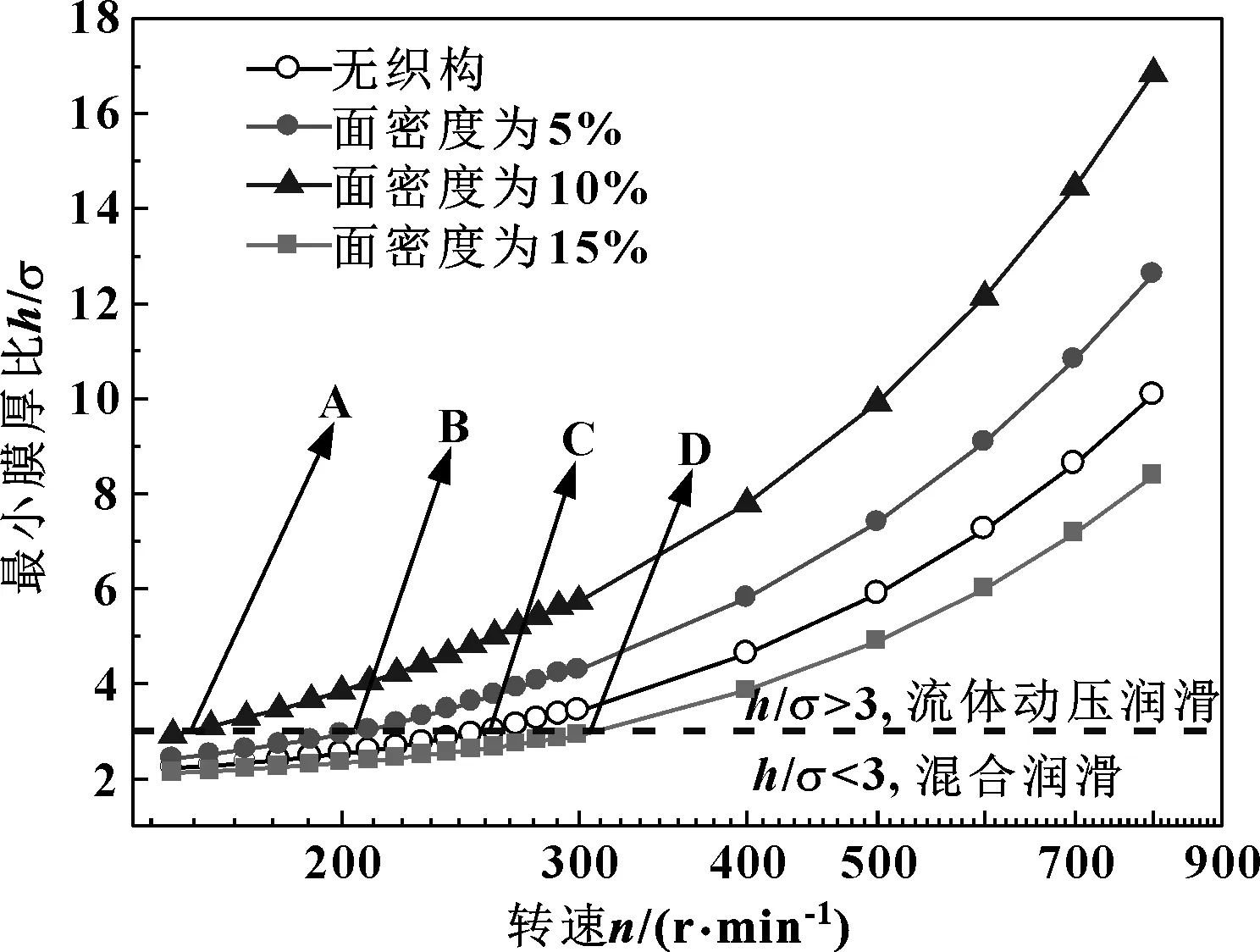
图6 织构面密度对最小膜厚的影响Fig 6 Effect of texture surface density on minimum film thickness ratio

图7所示为织构深度hp=10 μm时，不同面密度下摩擦因数随转速的变化曲线。

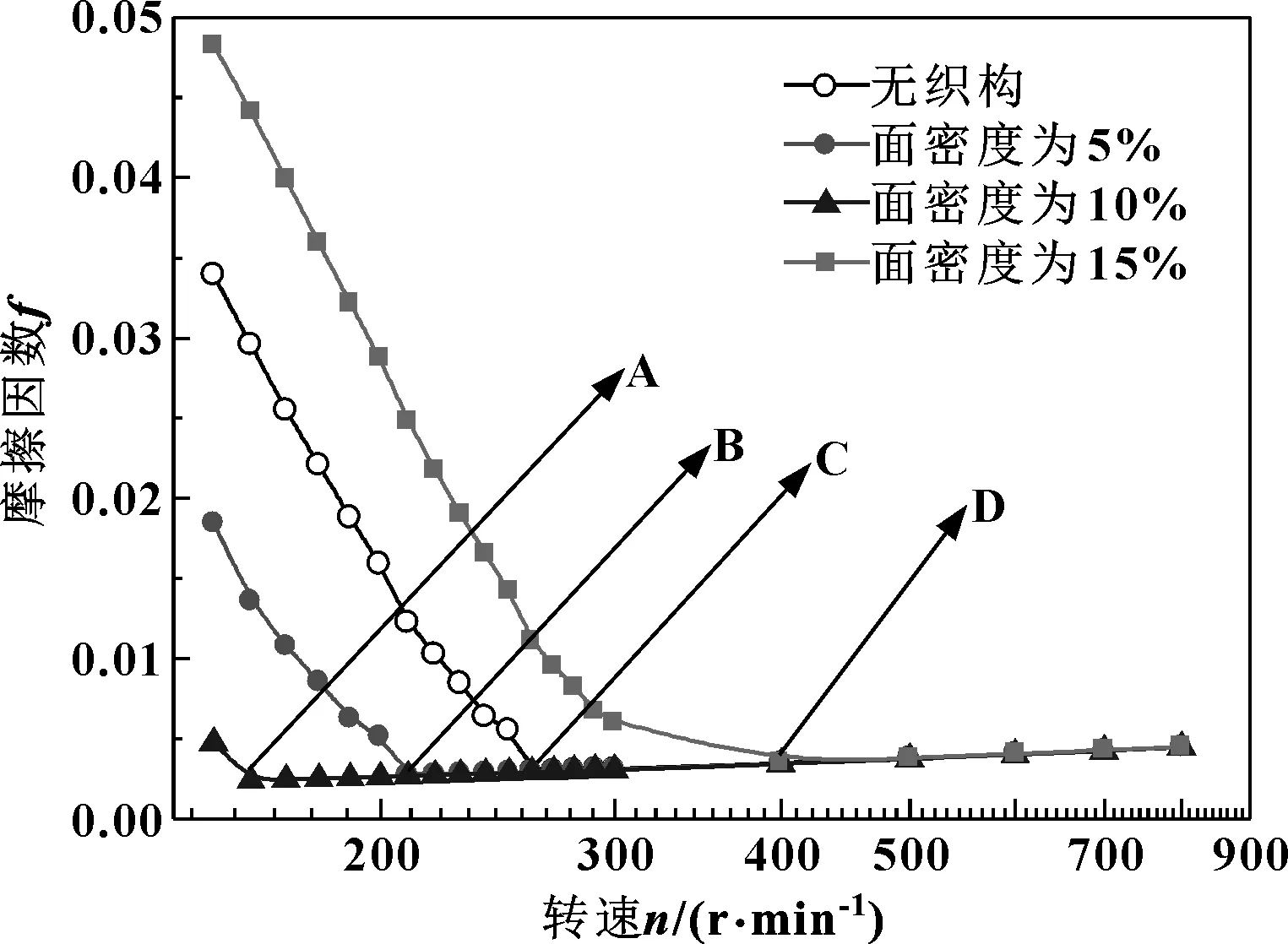
图7 织构面密度对摩擦因数的影响Fig 7 Influence of texture surface density on friction coefficient

可以得出，当转速相同而面密度Sp<15%时，摩擦因数随面密度的增加，呈现减小的趋势，面密度Sp=10%时摩擦因数最小，并且在最低转速下由混合润滑进入流体动压润滑；但面密度Sp=15%时轴承摩擦因数比无织构时还有所增加，且在较高的转速下才能进入流体动压润滑状态。其原因在于：随着织构面密度的增大，织构内收敛楔形间隙产生的流体动压效应升高，造成了水膜厚度的增加和摩擦因数的减小；但过大的间距会使压力峰值降低，减弱流体动压效应，从而造成水膜厚度的减小和摩擦因数的增大。

由此得出：织构面密度是影响水润滑轴承摩擦因数的另一重要参数，面密度在一定范围内能有效降低摩擦因数，增加水膜厚度，使轴承在降低转速下进入流体动压润滑。

3 结论

建立带有表面织构的水润滑轴承混合润滑模型，并采用JFO空化边界条件进行数值求解，绘制了不同织构参数下轴承的Stribeck曲线，得出如下结论：

(1)表面织构的深径比和面密度是影响水润滑轴承摩擦因数及改善润滑性能的重要参数，但是织构的加入并不一定能减小摩擦因数。

(2)表面织构的面密度和深径比存在最优值，能使水润滑轴承获得最大的膜厚比与最小的摩擦因数，并在较低的转速下由混合润滑状态进入流体动压润滑状态。