K均值聚类改进与行驶工况构建研究

刘子谭 朱平 刘旭鹏 刘钊

（1.上海交通大学，上海 200240；2.上汽大众汽车有限公司，上海 201805）

1 前言

行驶工况是通过数据分析所构建的一个区域内一系列代表性的速度-时间数据，可以模拟真实的交通状况，以测试车辆尾气排放和燃料消耗。此外，其在交通协同控制、新车评价、风险评估和车辆的设计、选型、匹配和控制策略等方面有着广泛的应用[1-3]。

常用的行驶工况构建方法是短行程法，将数据划分成短行程片段，通过分析片段特征参数组合生成对应的行驶工况[4]。Lin 等采用短片段划分以及随机过程选择方法构建了行驶工况[5]。Fotouhi和Montazaeri 描述了基于短行程和K 均值聚类方法的汽车行驶工况构建过程，将开发的行驶工况特征与FTP-75、联合国欧洲经济委员会（Economic Commission for Europe，ECE）汽车法规和市郊循环工况（Extra Urban Driving Cycle，EUDC）进行了对比分析[6]。同济大学胡志远利用短行程、主成分分析、聚类分析等方法对上海市公交车进行研究，生成了最优短行程组合[7]。吉林大学秦大同等利用K 均值聚类算法与工况选择方法构建了较为精准的区域行驶工况[8]。李孟良等学者采集了北京、上海和广州车辆行驶速度等运动学特征，生成3个城市的工况并与ECE 15 工况相比较，说明中国城市行驶工况的特点[9]。彭美春等学者沿广州市中心区2 条典型公交线路进行试验，得到广州市公交车行驶工况并与欧洲瞬态循环（European Transient Cycle，ETC）城市工况进行了比较[10]。

我国汽车行驶工况方面的标准、试验方法、测试手段等全面沿用新欧洲行驶工况（New European Driving Cycle，NEDC），但其与中国的相似程度较低。李孟良等学者根据采集的北京市、上海市、广州市实际道路工况提出了QC/T 759—2006《汽车试验用城市运转循环》，但该工况提出较早，对当前广州市实际交通状况的适应性有待验证。因此，构建较为精确的广州市交通特征行驶工况对于分析广州市交通状态，以及广州市机动车排放测试、新车仿真有着重要价值。

本文利用短行程法、主成分分析及聚类方法，并针对K均值聚类稳定性较差的缺陷进行改进研究，将改进后的聚类方法应用于工况构建，生成了广州市行驶工况并与美国、欧洲等地区的典型行驶工况进行比较，给出广州市工况的特点。

2 行驶工况构建流程与理论方法

2.1 短行程法构建工况流程

先将数据划分成短行程片段，再根据片段特征参数，将具有相似特征的片段聚合成3 类，对生成的类数据集采用一定的片段拼接算法生成行驶工况[7,11]，本文采用的行驶工况构建流程如图1所示。

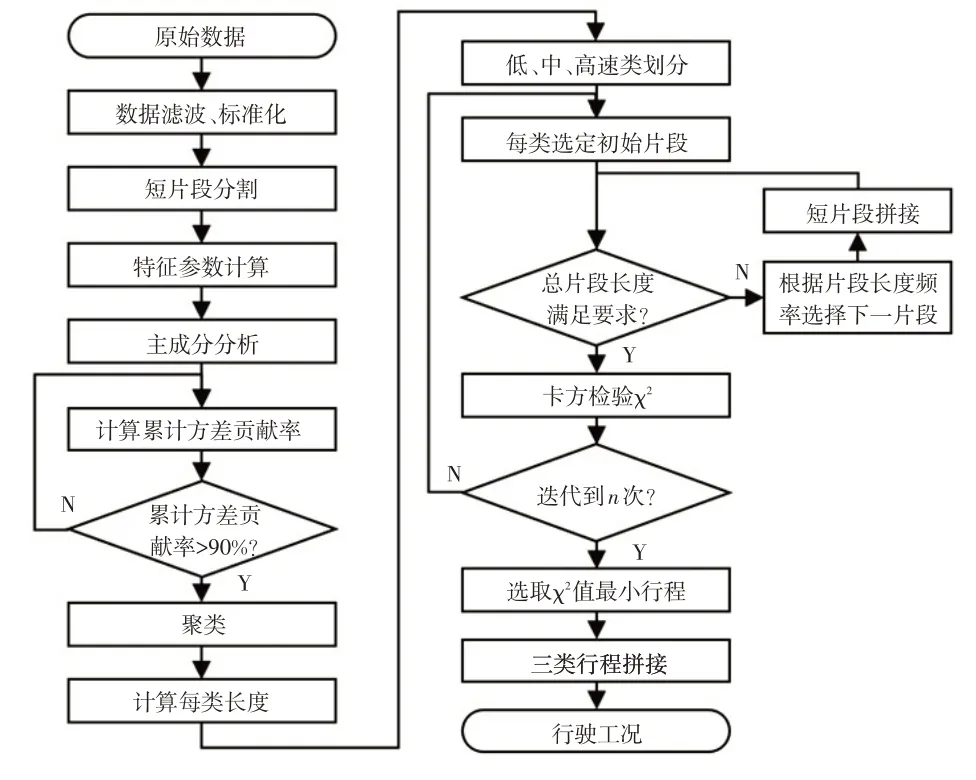
图1 短行程构建流程

2.2 主成分分析

主成分分析法是一种多元统计方法，可以通过较少的综合变量尽可能多地反映原变量的信息。本文数据量大、数据维度多，且各维度之间有一定的信息重叠，通过主成分分析能够大幅减小数据规模，提高计算效率。

2.3 聚类理论

K 均值聚类（K-Means）作为最常用的聚类算法之一，具有算法简单、收敛速度快等优点。K 中心点聚类（K-Medoids）与K 均值聚类不同，选用类中位置居于最中心的对象作为迭代过程新聚类中心。模糊C 均值算法（Fuzzy C-Means，FCM）与K 均值聚类方法的主要区别在于FCM采用模糊划分，使得每个数据点用[0,1]区间内的隶属度来确定其属于各个类的程度。高斯混合模型（Gaussian Mixture Models，GMM）每个维度用均值和标准差（方差）描述簇的形状。

3 数据采集与预处理

3.1 数据采集

行驶工况的构建采用数据解析方法，对于样本量和样本质量有一定要求。表1 显示了收集数据的基本信息。每日数据由多个短行程组成，数据记录从汽车起动开始到汽车熄火结束。车型选择需要考虑用户覆盖不同的职业和年龄段，选择了A0 级、A 级、B 级车型共计20 辆。经过6 个月的广泛采样，共采集了广州市2 800余万条行驶数据。

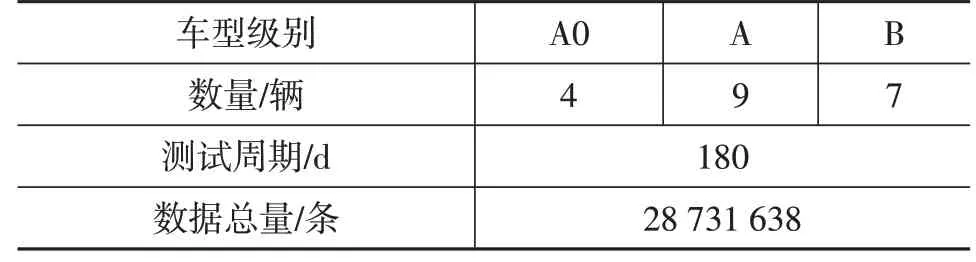
表1 数据采集基本信息

3.2 数据预处理

短行程是汽车行驶过程中一个怠速开始到下一个怠速开始的运动学片段，可以看作怠速段与运动段的组合。通过道路试验得到汽车运行过程中的速度-时间数据，将数据分割成111 321 个短行程片段。为了描述短片段的特征，选用行驶距离、最高车速、最大加速度、最小减速度、平均加速度、平均减速度、加速度标准差、平均车速、平均运行车速、速度标准差、减速时间、加速时间、怠速时间、巡航时间、片段时间作为特征参数。

对原始数据进行主成分分析，结果如表2所示。选择使累计贡献率达到90%的前4 个主成分代表所有原始变量，使得主成分方差贡献率达到91.28%。

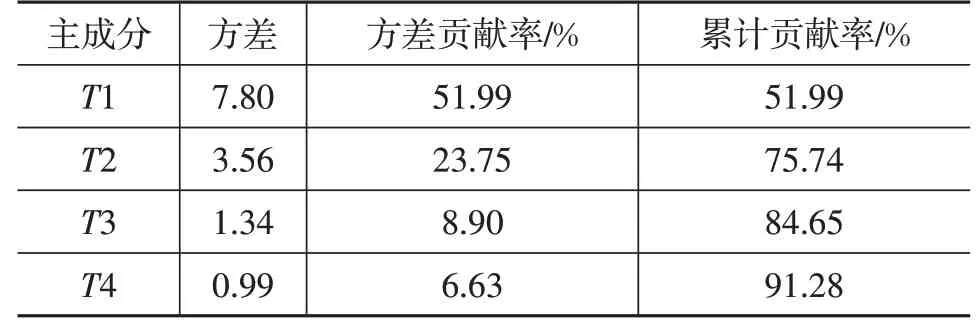
表2 主成分贡献率及累计贡献百分率

4 聚类方法对比分析

聚类方法多种多样，其效果对行驶工况构建的精度也有重要影响。行驶工况构建过程中涉及大量数据的处理，根据聚类方法适用性选取K 均值聚类、K 中心点聚类、模糊聚类与高斯混合聚类进行比较分析。

为了判断聚类方法的优劣，聚类中心设为3 个，分别运用4种方法进行10次聚类并对结果进行计算分析。

4.1 聚类稳定性

短片段的速度特征是描述片段的重要参数，每个类的速度分布也能较直接地的反映聚类效果，10 次聚类每一类的最大速度频率分布如图2所示。

图2 最大速度频率分布

为了描述聚类稳定性，计算相关变量，比较聚类中心偏差值ε，ε越小，稳定性越高。计算公式为：

式中，K为聚类中心数量；N为试验次数；nij为第i次试验第j类聚类中心坐标；-n为N次试验的平均值。

ε的计算结果如表3所示。由图2、表3可知，4种方法生成的类速度分布整体趋势相似，且每类的速度分布有明显差别，因此可将3 类划分为低、中、高速类。此外，结果反映出了聚类结果的稳定性：模糊聚类10次聚类频率分布曲线几乎重合，偏差小、稳定性好；K中心点聚类次之；高斯混合较为发散；K 均值聚类则出现了混乱的结果，偏差值较大。

表3 聚类稳定性评价指标

4.2 样本适应性

速度、加速度联合概率分布是描述工况状态的重要指标，也是短行程拼接筛选的依据。每一类内部速度、加速度联合分布差异越小，越易筛选到与该类联合分布匹配的短片段。

轮廓系数（Silhouette Coefficient）是描述轮廓团聚性的变量。对于单个样本，计算公式为：

式中，a为其与同类别中其他样本的平均距离；b为其与距离最近的不同类别中样本的平均距离。

对于一个样本集合，轮廓系数是所有样本轮廓系数的平均值。轮廓系数取值范围是[0,1]，同类别样本距离越相近且不同类别样本距离越远，即数值越大，团聚性越高。

图3所示为4种聚类方法平均速度与平均加速度联合分布情况，表4 所示为4 种适应性指标。可得两种K聚类中各类的速度、加速度联合分布具有更明显的团聚性，低速类的平均加速度整体较高，高速类的平均加速度整体较低，这与实际低、高速行驶状态相一致，说明K聚类更适合该样本，其中K均值聚类样本适应性最好。

4.3 聚类时间

表5 所示为4 种聚类方法的平均聚类时间，由图5可以明显看出K 均值聚类在计算时间方面较其他聚类算法有明显优势。

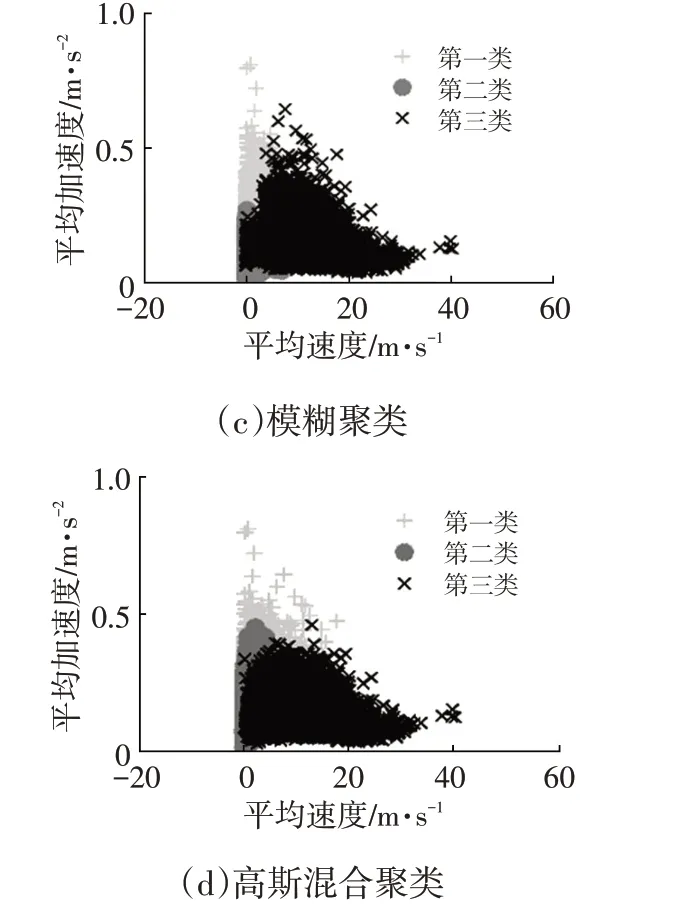
图3 平均速度与平均加速度联合分布

表4 聚类适应性评价指标

表5 聚类平均时间

4.4 紧密性与分离性指标

为了量化描述聚类效果以及聚类的稳定性，采用紧密性（Compactness）CP与分离性（Separation）SP指标。前者描述各点到聚类中心的平均距离，越小说明同一类紧密度越高，效果越好；后者描述各聚类中心两两之间的平均距离，越大说明不同类间隔性越高，效果越好。紧密型指标和分离性指标的计算方法分别为：

式中，k为聚类中心个数；Ωi为第i个聚类集合；wi为第i个聚类中心；xi为第i个聚类所包含的元素。

表6 所示为4 种聚类CP与SP指标的均值与方差。4 种聚类方法得到的CP与SP指标均值接近，且聚类紧密度与间隔度此消彼长，但指标方差差别较大，模糊聚类方差最小，K 中心点聚类次之，高斯混合聚类最大，K均值聚类较大，这与稳定性指标分析结果相吻合。

图4、图5 分别 为4 种方法10 次 聚类CP值 与SP值。10次聚类结果中模糊聚类与K中心点聚类指标变动小，高斯混合整体波动较大，而K 均值聚类出现了尖点。因此，4 种聚类方法准确性效果相似，但稳定性有差异。其中，模糊聚类、K中心点聚类稳定性较好，高斯混合聚类较差，而K均值聚类除了一次偏差较大的不合理聚类外，其余结果较稳定。

表6 CP与SP均值与方差

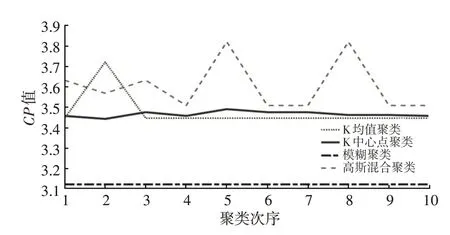
图4 10次聚类CP值

图5 10次聚类SP值

综上，K均值聚类综合性能较优，样本适应性最好，聚类效率最高，但其稳定性有待改进。

5 K均值聚类改进研究

K均值聚类对初始值较敏感，结果发生突变的主要原因是初始聚类中心选到了数据集中的边缘点或者孤立点。针对这一问题，对数据集进行统计学分析。

在数据空间中，通常认为处于低密度区域的点为噪声点[12]。由表7主成分统计特征参数可得，主成分均值均为0，每一维数据具有正态性，且其置信度90%区间范围相对于原有区间范围大幅缩小。每个维度都采用置信度90%区间范围计算的联合分布概率为75.98%，点平均密度增加为原来的15 万倍，即舍弃了原空间中的边缘点与孤立点。

因此采用置信度90%区间作为K 均值聚类初始聚类中心的选择区间，10次聚类结果如表8所示，改进前、后聚类中心偏差减小，轮廓系数增加，CP和SP指标方差减小，稳定性提高显著，且计算效率相近。

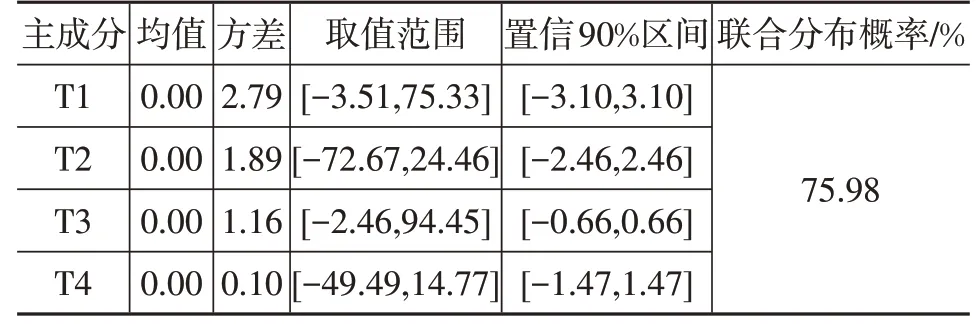
表7 数据集统计特征参数

表8 改进前、后参数对比

6 行驶工况构建验证

根据某汽车企业的测试标准，行驶工况时间长度为1 800 s，其中低、中、高速时间分别为413 s、920 s和467 s，利用改进的K均值聚类法构建广州市行驶工况如图6示。

选取9 个指标对生成的工况进行验证，表9 为试验数据与拟合工况参数对比结果。可见，改进方法生成的广州市道路行驶工况各项误差均小于10%，低、中、高速类以及整体平均相对误差为小于6%，运动学特征较吻合。

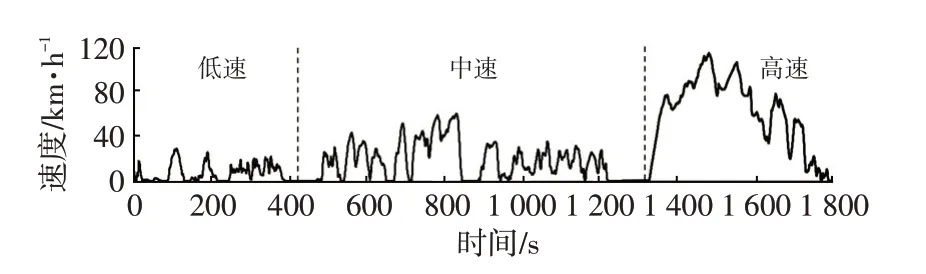
图6 广州市行驶工况

行驶工况的主要运动学特征为汽车行驶的速度和加速度，且两者具有强相关性。因此，能准确描述数据集运动学信息的行驶工况应具有与原数据集相似的速度-加速度联合分布。由表9 可知，广州市低、中、高速以及整体速度-加速度联合分布概率卡方检验值均小于0.1，即卡方检验合格，说明拟合工况与试验数据显著相关。通过运动学特征比较以及速度-加速度频率分布卡方检验证明，利用本研究方法所得到的行驶工况能够反映实际道路交通状况。

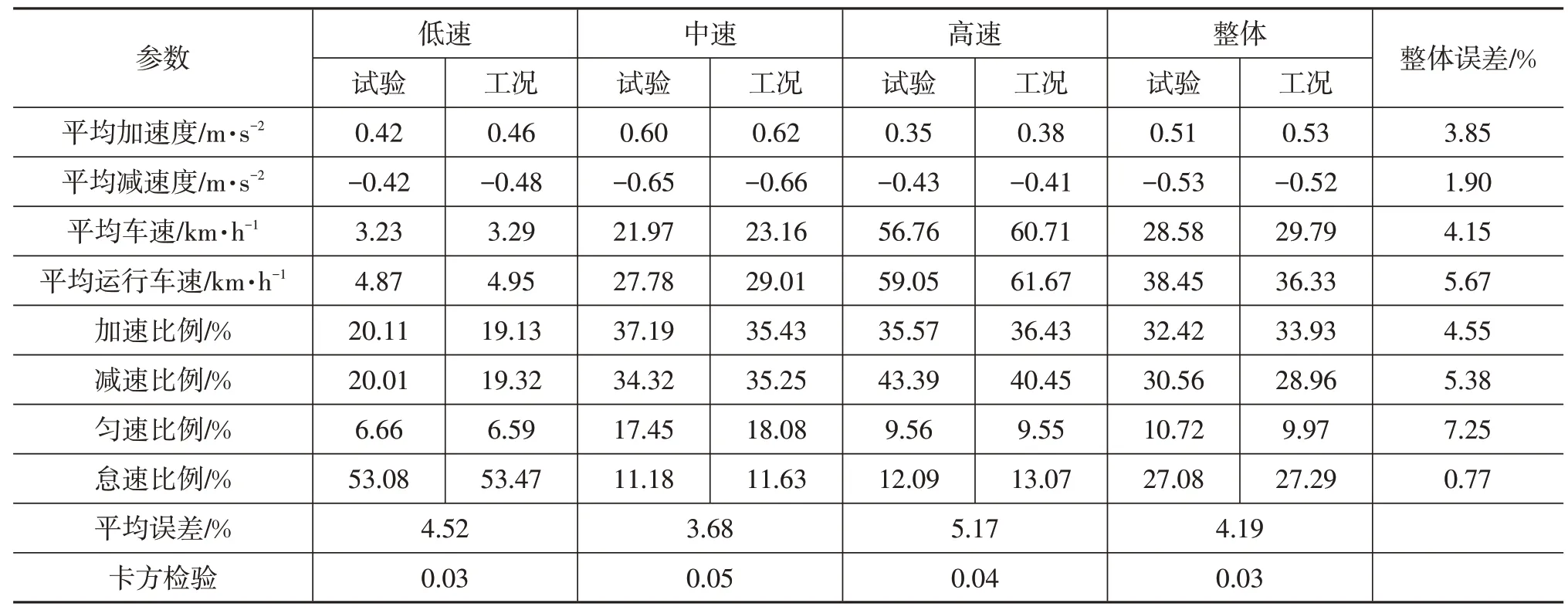
表9 试验与拟合工况参数对比

将广州市行驶工况与国际上常用的行驶工况全球统一轻型车油耗测试规程（World Light Vehicle Test Procedure，WLTP）、NEDC、美国城市道路循环（Urban Dynamometer Driving Schedule，UDDS）、日本工况JC08、中国汽车试验用城市运转循环（QC/T 759—2016）相比较，结果如图7所示。由图7可以看出：广州市行驶工况怠速比例高达27%，速度分布频率随着速度的提高逐渐降低，最高速度约为110 km/h；而UDDS、NEDC 以及QC/T 759 循环中速段频率高于低速段；WLTP 速度分布较平均；JC08 低速分布频率最高。QC/T 759 循环最高速度为90 km/h，显然不符合广州市实际交通工况。因此，广州市工况低速段比例较高、平均速度较低，与其他代表性工况有一定差异。

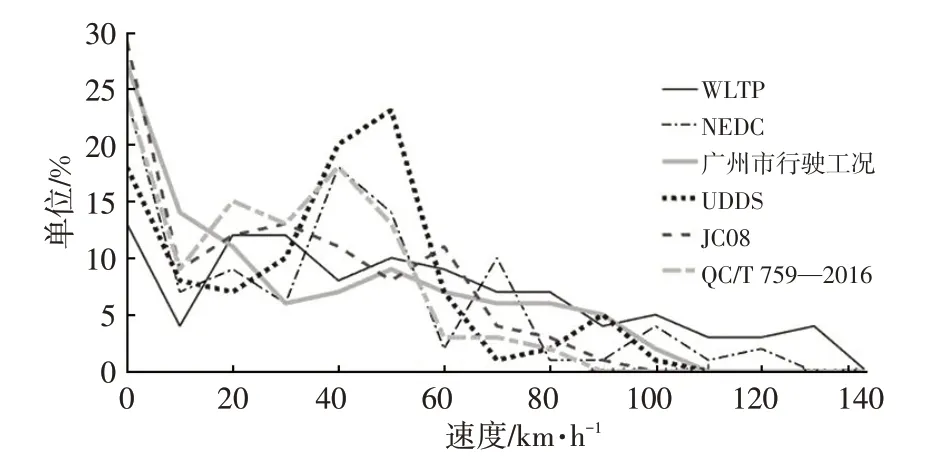
图7 广州市行驶工况与世界典型行驶工况速度频率分布对比

对广州市工况的相关运动学参数分析可得，广州市车辆运行加、减速比例高达60%以上，加、减速频繁，起停过程多、怠速比例高，交通状况较拥堵，相应的燃油消耗和尾气排放高，交通状况有待改善。因此，中国现行NEDC 以及QC/T 759 工况不能完全反映广州市的实际交通状况，而本文构建的广州市行驶工况代表性、准确度高。

7 结束语

本文以广州市为例，利用短行程法、主成分分析法对采集的数据集进行处理。对4 种聚类方法进行比较分析，并对K 均值聚类进行了改进，改进算法稳定性大幅提高，生成的行驶工况平均相对误差小于6%。

通过分析广州市试验数据与行驶工况的特征参数，验证了工况的准确性。广州市工况与世界典型工况对比结果表明，广州市行驶工况加减速比例高、低速段占主导、交通状态较拥堵，与其他代表性工况有一定差异。本文构建的工况在速度分布等方面较中国现行的测试工况NEDC 和QC/T 759—2016 更符合广州市的交通特点。