复数三角形式的教学与探究

贾凌云

(广东省惠州市黄冈中学惠州学校 516001)

一、教材地位与背景分析

2018年高考改革明确提出高中教学中增加复数的三角形式.通过引入复数三角形式,可以简化复数乘除运算,彻底解决复数乘方开方运算,使复数知识的教学更完善,将复数与三角知识综合,不但对三角公式能起到巩固作用,并使某些知识如倍角、解方程等知识得到发展与深化,可以衔接高次方程的解法,使学生解方程的能力得到拓展.教师在引导学生进行复数三角形式的乘除运算的教学时,可以轻易得出棣莫弗定理,如果再适当介绍欧拉公式,得出复数指数形式,三角形式和指数形式可以形成顺利对接!或者将二项式定理用于棣莫弗公式,实现复数与二项式定理的沟通,为学生展开了一副非常壮阔的数学前景,可以为学生数学核心素养的形成起到了引领的作用.

二、对教材内容操作的探究

能力的培养是教学活动的中心，理解教材是一个复杂的思维过程，为了便于学生准确地理解教材，正确思维，教师要善于运用比较、分析、综合等逻辑思维方法和归纳、演绎等逻辑推理形式，来引导和组织学生的思维过程，让学生在课堂中自己去观察、去探索、去发现问题并解决问题，为了达到这样的教学目标，精心设计的教学思路就是一个老师对学生最好的帮助，下面是我的一个设想.

首先, 在复平面内将复数的代数形式转化成三角形式，从而得复数的到三角形式的定义,即

其次，设z1=r1(cosθ1+isinθ1),z2=r2(cosθ2+isinθ2),通过使z1=z2=z得到

z2=r2(cos2θ+isin2θ) ,再继续推导出z3=r3(cos3θ+isin3θ),……

从而归纳出棣莫弗公式zn=rn(cosnθ+isinnθ).

再次,引导学生用数学归纳法对棣莫弗公式进行证明:

第四,介绍欧拉公式eiθ=cosθ+isinθ,并代入z=r(cosθ+isinθ)得到复数的指数形式z=reiθ,在指数形式下再来证明棣莫弗定理：

证明：zn=rn(cosθ+isinθ)n=rn(eiθ)n=rneiθn=rn(cosnθ+isinnθ).

这个证明方法实在太漂亮了，哪个学生不会因此爱上数学？

对于多数学生而言,复数三角形式的教学到此完成一个段落,但是对于基础好的学生,可以继续拓展深化.

第五,将(cosθ+isinθ)n=cosnθ+isinnθ的左边用二项式定理展开得到

本文样本来自《中国工业企业数据库》，样本时间区间为2002～2006年。剔除相关变量缺失、数据明显错误(比如员工数量为0，资产小于0)样本，最终形成时间范围为2002～2006年的平衡面板数据，共计77 705家企业，所属行业均为制造业。

在此，复数与二项式定理完美结合，为学生开启了一扇领略数学之美的智慧之窗.

三、对教材其他模块知识的深化

概念的掌握并不是一次完成的，它是一个由浅入深、由易到难的循序渐进的过程，学生学习了复数的三角形式后容易将一些含有三角符号的复数表达式混同于复数的三角形式.为使学生准确认识复数三角形式的结构，教师设计问题帮助学生区别其本质与非本质的属性是必不可少的关键环节.

例如：将复数z=1-cosθ+isinθ(0<θ<π)转化为标准的三角形式.

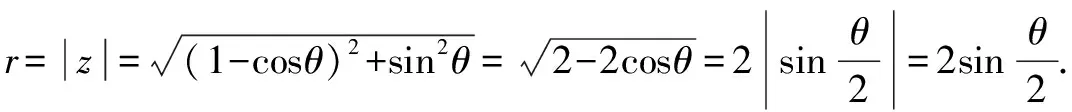
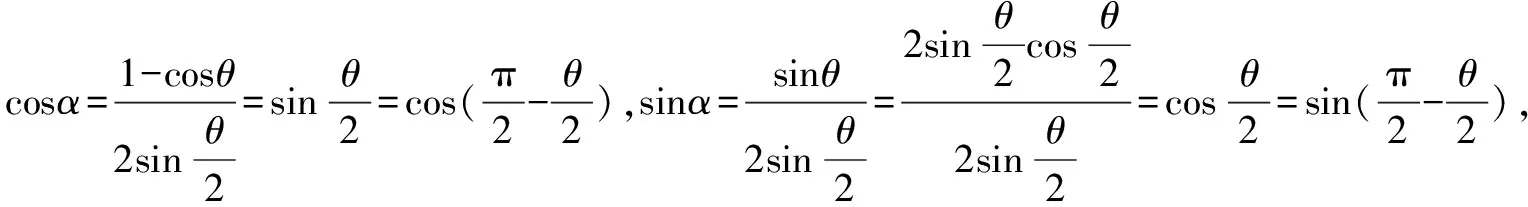
此时复数z满足了“模非负，角相同，余弦前，加号连”，是标准的三角形式.通过这个问题的分析，复数三角形式的本质特点清晰得呈现出来：“模非负，角相同，余弦前，加号连”.教学中通过将代数形式的复数转化为三角形式，训练了学生的思维能力，也深化和巩固了三角函数，对数学必修四中三角诱导公式及三角恒等变形能力有很大的促进.

即eiπ+1=0，这个等式将数学中最常用的五个数联系起来的，被称为欧拉恒等式.

纵观这节课的教学设计，紧紧围绕复数的三角形式这一主题，依照学生的认识规律，由浅入深地剖析概念，用例题辨析易错点，通过知识点间的新旧交融、步步设疑、点拨诱导、归纳类比、适度拓展的教学策略，启发学生积极思考，不断探索，用老师的教促进学生学，即教学生学！让课堂成为学生思维活动展示的舞台.数学教育的终极目标是“用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界”.通过对复数三角形式的教学，我们可以向学生充分展示数学之美，是新课标中落实数学核心素养的绝好的载体.