无传感器永磁同步电动机转矩脉动抑制

陈日垚，王金昌，徐建英，陈耀文，陈 雪

(辽宁科技大学，鞍山 114051)

0 引 言

永磁同步电动机(以下简称PMSM)具有结构简单、运行可靠、功率密度高、体积小、噪声小等优点，因而被广泛应用[1]。对于PMSM矢量控制系统，由于反电动势畸变、磁路饱和、磁链非正弦分布等因素，即使变频器拥有理想的输出特性，也会产生转矩脉动。特别是PMSM由转子磁链非正弦引起的非正弦感应电动势产生的转矩脉动，相对于转子转速具有周期性的特点。转矩脉动存在于整个控制过程中，针对此种问题，国内外学者提出很多有效的方法。如对电机结构进行分析，采用新的定子设计方法减小电机的齿槽转矩[2]，或是应用有限元法，优化电机内部结构来减小转矩脉动[3]。文献[4]对电机6次脉动信号进行采集，通过数学模型产生补偿电流，对特定频率的脉动信号进行抑制。文献[5]采用转子位置检测器，而不使用转矩传感器，通过电机的逆模型获得抑制脉动的补偿电流，给出了6次，12次谐波转矩抑制的补偿电流解析表达式和实验结果，但没有考虑对18次等更高次谐波转矩脉动进行抑制。文献[6]运用自学习的方法对脉动信号进行补偿。为削弱由开关频率引起的脉动，文献[7]通过改变开关表的开关频率来降低转矩脉动。

包含位置传感器装置的系统具有体积大、成本高、耐环境能力差等缺点，无位置传感器PMSM调速系统避免了这些缺点，越来越引起人们的关注。在PMSM的位置估计方法中，对反电动势进行积分的磁通估计方法已经成为中、高速范围位置估计的主流。文献[8]提出一种基于电机磁链的位置估计方法，采用近似积分环节替代纯积分环节，通过全通滤波器进行相位校正，使其较准确地实现反电动势的积分运算，获取磁通向量得到位置信息。本文研究一种无转矩传感器、无位置传感器，即无传感器的PMSM转矩脉动抑制方法。它采用一种简单的信号提取方法，对于特定次数谐波电流进行补偿，通过快速滑模控制器进行速度控制，增加鲁棒性；通过近似积分功能代替纯积分得到磁通估计值，全通滤波器保证了近似积分的相位滞后特性。在全频段上，能够维持磁通幅值恒定，进行相位补偿。动态过程也可以保证估计的准确性。仿真实验验证了这种无传感器PMSM转矩脉动抑制调速系统的有效性与可行性。

1 PMSM调速系统的数学模型

1.1 PMSM的数学模型

基于以下假设：

(1) 定子线圈产生磁场沿气隙为正弦分布；

(2) 忽略定子齿槽对于转子角度的影响；

(3) 铁心磁路为线性(非饱和)；

(4) 温度和频率变化对于电阻电感无影响。

得到定子电压表达式：

(1)

(2)

式中：ud是d轴电压；uq是q轴电压；id是d轴电流；iq是q轴电流；R是定子电阻；Ld是d轴电感；Lq是q轴电感；p是微分算子；T是电机转矩；TL是负载转矩；p是极对数；J是转动惯量；ω是电角速度；em为2×1向量，是考虑永磁谐波磁链时在电枢绕组里产生的感生电动势。

θ为图1所示d轴和α轴(u轴)的夹角[4]。

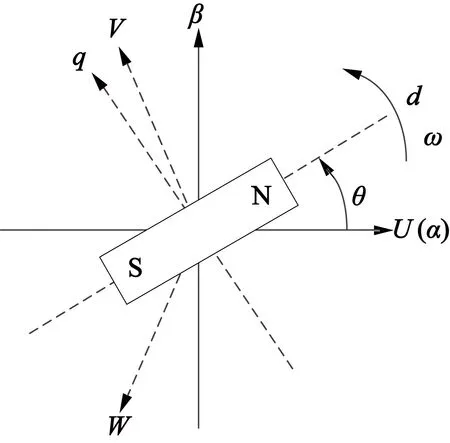
图1 三种参考坐标系

upk，unk的表达式如下：

(3)

(4)

式中：k为非负整数。

1.2 非正弦感应电流的补偿方法

电机转子永久磁场的空间谐波磁通，会在电枢绕组中产生相应次数的谐波感生电动势，即5次，7次，11次，13次，17次，19次，23次，25次…谐波感生电动势，从而在电枢绕组中产生相应次数的谐波感生电流，造成转矩脉动。电机电枢5次谐波电流产生与基波磁场逆相序的5倍于基波磁场旋转速度的谐波旋转磁场(与基波磁场反向)，而电枢7次谐波电流产生与基波磁场正相序的7倍于基波磁场旋转速度的谐波旋转磁场(与基波磁场同向)。同理，11次，13次，17次，19次谐波电流分别产生相应次数的谐波旋转磁场。通过相数变换和旋转变换使三相PMSM电枢绕组变换为两相同步旋转绕组，d轴定在转子永磁基波磁场的轴线上，则5次，7次谐波磁场会在绕组中产生6倍于基波频率的电流，从而造成6倍于基波转矩的转矩脉动。同理，11次，13次谐波磁场造成12倍于基波转矩频率的转矩脉动。为了获得更高的谐波转矩脉动抑制控制精度，还应该考虑17次，19次谐波磁场造成的18倍于基波转矩频率的转矩脉动。这时的转子磁通、电枢感生电动势、电机转矩表达式分别如下[4-5]：

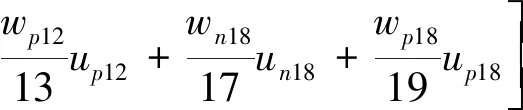
(5)

em=ωψfG[up0-wn6un6+wp6up6-

wn12un12+wp12up12-wn18un18+wp18up18]

(6)

T=Tr+Te=

wn12un12+wp12up12-wn18un18+wp18up18]

(7)

式中：

(8)

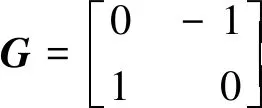
(9)

当考虑更高次谐波，即18次转矩脉动(电磁转矩脉动，磁阻转矩脉动)时，系统的数学模型如式(5)～式(7)所示。为抑制18次谐波电流引起的转矩脉动，18次谐波补偿电流推导如下：

em=ωψfG[up0-wn6un6+wp6up6-wn12un12+wp12up12-wn18un18+wp18up18]=

[emf+emh6+emh12+emh18]

(10)

(11)

为抑制电动机的电磁转矩脉动，有：

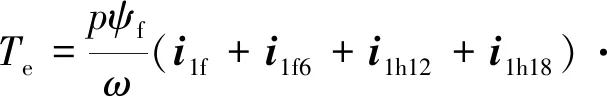
(emf+emf6+emf12+emf18)

(12)

通常高频成分的幅值，比基波成分幅值小得多，那么高频波之间的乘积更小，可以忽略，式(12)可以近似整理：

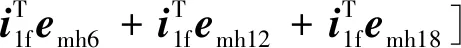
(13)

式(13)的右边第1项是产生电磁转矩的基波成分，第2、5项是6次脉动成分；第3、6项是12次脉动成分；第4、7项是18次脉动成分。18次谐波转矩脉动成分为0的条件是：

(14)

式(12)代入式(14)，可得18次高频电流：

iqh18=-iqf(wp18-wn18)cos(18θ)+

idf(wp18+wn18)sin(18θ)

(15)

由此，得到使得18次脉动成分变成0的q轴的脉动补偿信号(电流补偿值)：

(16)

6次、12次的电流补偿值见文献[5]，这时有补偿电流值：

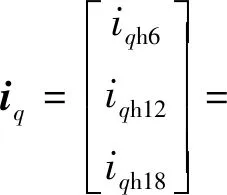
(17)

为了抑制由电机凸极性引起的磁阻转矩脉动，通过式(7)的第一项和式(11)可得：

Tr=2pLm(idf+idh6+idh12+idh18)·

(iqf+iqf6+iqf12+iqf18)

(18)

式(18)中，高次谐波成分之间的乘积非常小，可以忽略，近似整理成下式：

Tr≈2pLm(idfiqf+idh6iqf+idfiqh6+idh12iqf+

idfiqh12+idh18iqf+idfiqh18)

(19)

式(19)括号中右边第1项意味着磁阻转矩基波成分，第2、3项是6次脉动成分；第4、5项是12次脉动成分；第6、7项是18次脉动成分。在式(19)中，18次脉动成分为0的条件如下：

idh18iqf+idfiqh18=0

(20)

18次高频谐波电流补偿值整理后可得：

(21)

6次、12次的d轴电流补偿值见文献[5]，这时有补偿电流值：

(22)

这时可以得到如下电流补偿值:

(23)

式中：q轴的高次谐波补偿值如式(18)所示。

1.3 基于全通滤波器(APF)的位置估计方法

(24)

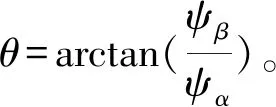
通过扩展磁链矢量的估计方法来实现转子位置估计：

(25)

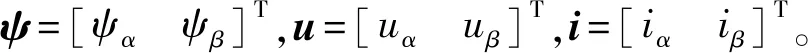
(26)

式中：ωc为位置估计系统的截止频率。

近似积分器的相位特性随着频率增加而从0到90°变化。在低频区域失去积分特性，变成了惯性环节，能够实现基于近似积分器稳态阶段的相位特性修正。如图2所示，用近似积分器替换纯积分器而产生的相位特性变化，通过arctan(ωc/ω)补偿由于位置估计迟滞效应造成的位置角度误差θ1，但是上述方法是基于近似积分器的稳态特性，并且需要定子电势u-Ri的角速度。ω的急剧变化使得在过渡过程中的相位修正存在一定误差，进而，在ω<ωc时，arctan(ωc/ω)的运算精度下降。所以在低速时，相位补偿精度会下降[8]。

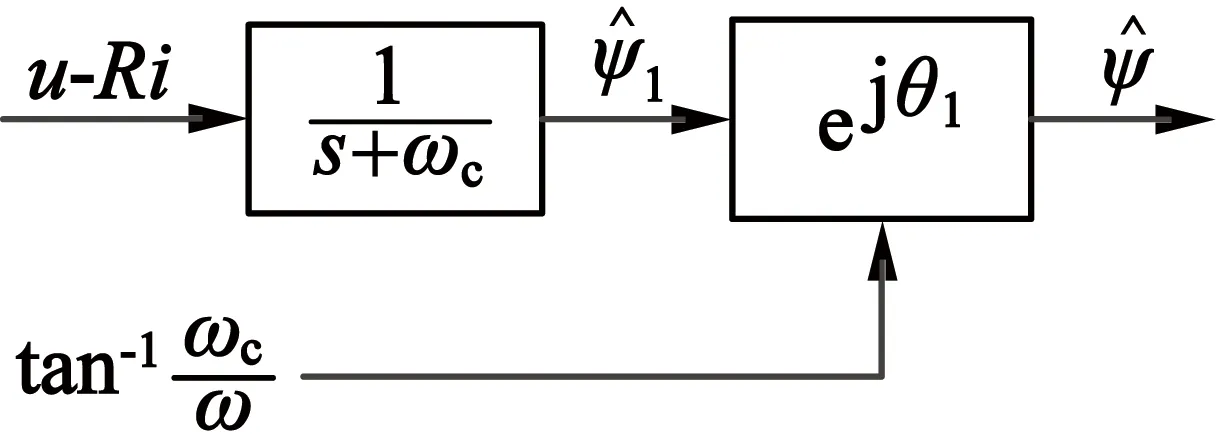
(a) 磁链估计原理框图

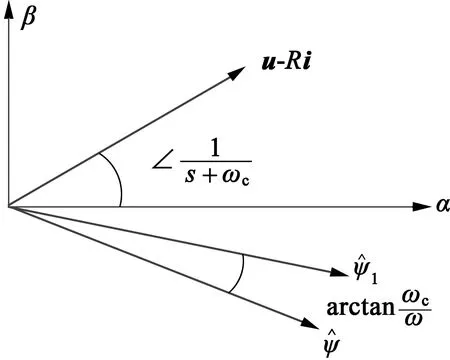
(b) 磁通估计的矢量图图2 传统的位置估计方法

1.4 全通相位变换器(APF)实现方法

结合近似积分器和APF，把传递函数的相位特性设定为-90°。根据近似积分器和APF的输出相位特性的点对称原理，为了突出近似积分器的优点，克服纯积分器的缺点，这里取ωc=400 rad/s，则有下式：

(27)

据此，必须：

(28)

得到k的参数值，k=282.8。

1.5 基于滑模的速度控制器

滑模控制是变结构控制系统的一种控制策略，与普通PID控制方法相比具有较好的鲁棒性。本文采用一种快速趋近律的滑模控制方式，来改善控制器的控制特性[9]。

首先对速度误差进行分析：

e=ω*-ω

(29)

定义上述速度误差为滑模面函数：

S=e=ω*-ω

(30)

得到速度滑模控制器的表达式：

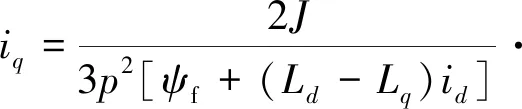
(31)

其中趋近律：

(32)

2 仿真实验

依图3搭建仿真平台，在Simulink环境下进行仿真，验证所提理论的正确性。电机参数如表1所示，速度环滑模控制器的参数：k=70，δ=1，ε=0.5，其中k值越大，系统响应越快，但是其值过大会造成系统振荡，ε决定了趋近的速度。采用模拟带通滤波器来提取谐波信号。由于PMSM的结构设计不同，高次谐波信号幅值并不相同，可以离线通过对磁链作傅里叶变换获得[10]。

图3 仿真系统整体框图表1 仿真电机各项参数表

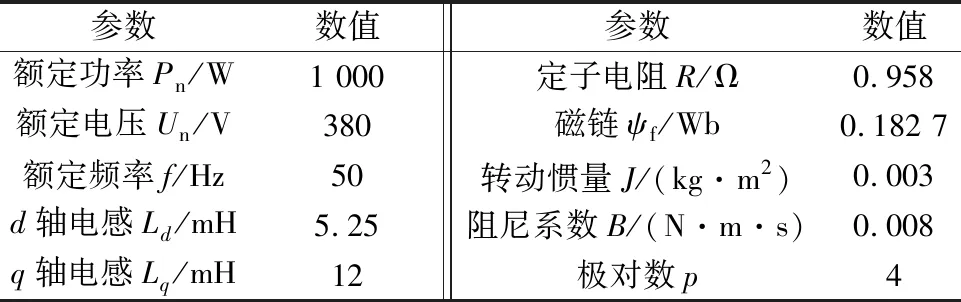
参数数值参数数值额定功率Pn/W1 000定子电阻R/Ω0.958额定电压Un/V380磁链ψf/Wb0.182 7额定频率f/Hz50转动惯量J/(kg·m2)0.003 d轴电感Ld/mH5.25阻尼系数B/(N·m·s)0.008 q轴电感Lq/mH12极对数p4

参考转速值1 000r/min，初始时刻转矩为0，在0.2s时突加10N·m负载转矩，进行系统仿真得到的控制系统各项波形，如图4～图6所示。

仿真实验得到的实际位置检测值和转子位置估计值的差值如图4所示。

图4 转子实际位置和估计位置差值图

转子实际速度检测值和估计的速度差值如图5所示。

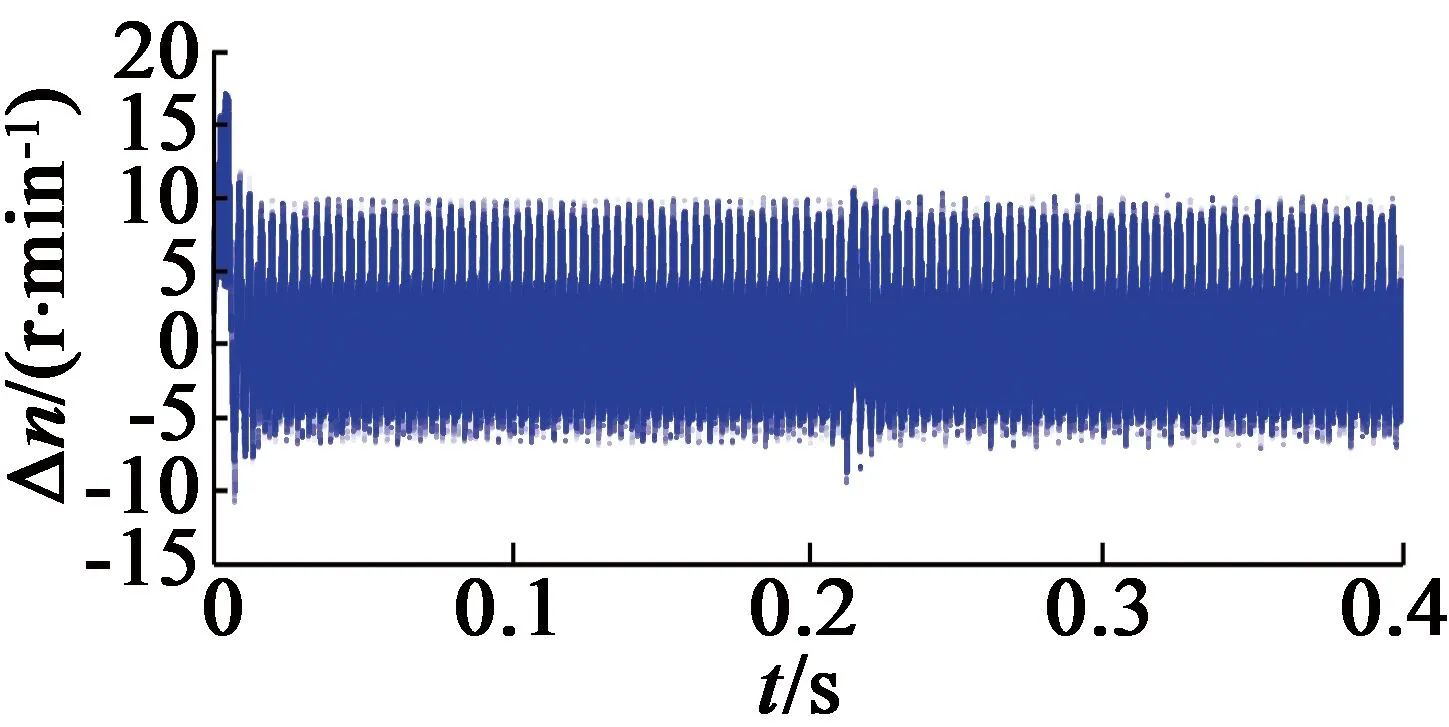
图5 转子实际速度和估计速度差值图

在进行位置估计时，分别将转子实际位置和估计位置对π/2取余，然后做差，即可得到图4。在电机起动过程阶段，位置估计器误差较大，经历一段时间后，误差减少，呈周期性变化。虽然转子位置估计值和实际值存在周期性的差值，但是相对给定转速来讲已经很小，可以忽略。同样，转速误差值在20r/min范围内波动。所以估计得到的位置和速度信息能够满足对系统的控制要求。

当给定转速为1 000r/min时，电动机起动过程经历了转矩建立、恒最大转矩升速、调速退饱和、进入转速调节阶段，滑模控制器的作用使得系统响应过程加快，大约在0.02s时达到稳定状态。转速超调不明显，同时转矩脉动抑制的算法模块，使得转矩输出更为平滑，如图6所示。0.2s时突加10N·m负载扰动。在突加负载瞬间，速度略有下降，电机的滑模控制器能迅速做出反应，增大电流值。在加入负载0.03s后速度达到稳定状态，速度输出稳定，波动范围小。

(a) 转矩变化

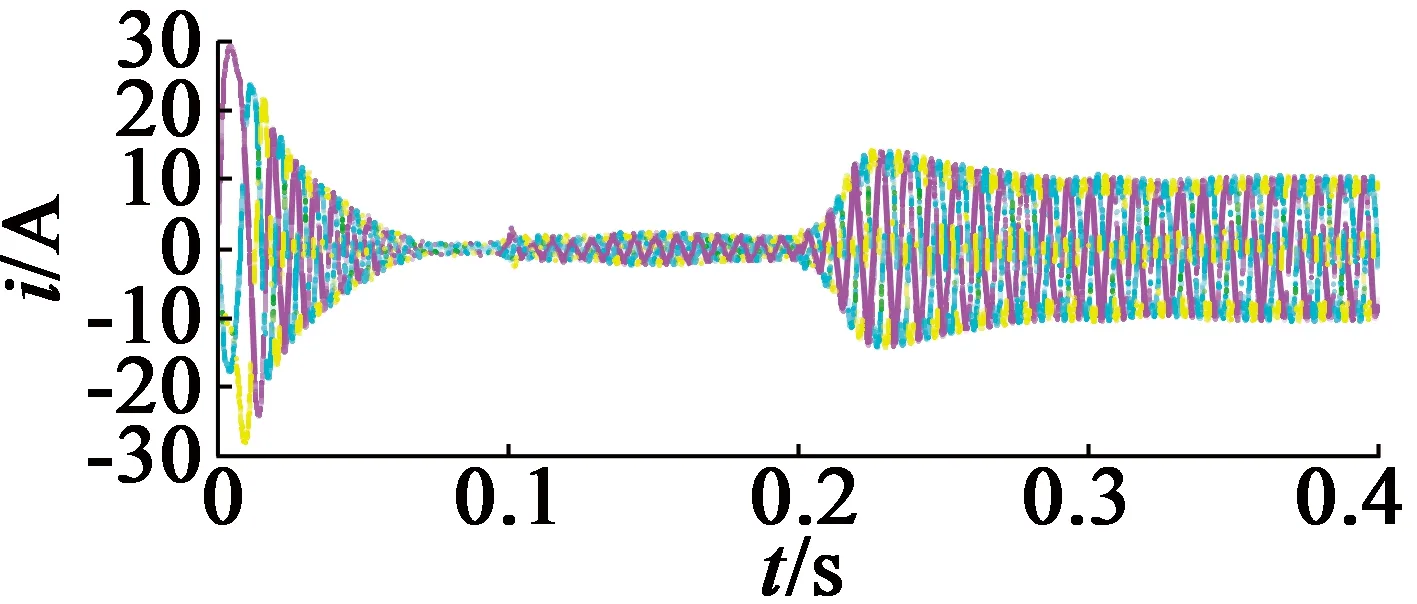
(b) 电流变化图6 无传感器PMSM转矩脉动抑制控制曲线

3 结 语

通过对凸极式PMSM转矩脉动的分析以及公式的推导，研究了一种无传感器的PMSM转矩脉动抑制方法。对d，q轴高次谐波电流的补偿获得了较理想的基波电流，使得转矩输出更为平稳。它不需要转矩传感器和位置传感器；电流补偿设计方法和结构相对简单，采用分别补偿6次，12次，18次转矩脉动的方法；一般可以补偿全转速范围内产生的转矩脉动，补偿次数愈高，得到的转矩输出愈平稳。

在位置估计器的设计上，使用带有全通滤波器的近似积分器，使其逼近纯积分的滞后相位，在全频范围内的位置估计信息更为精准。本文的无位置传感器、无转矩传感器的PMSM调速系统，运用一种快速滑模控制器，使得系统响应过程更快，提高了系统的抗干扰性。最后通过仿真实验验证了本文方法的可行性和有效性。