双转子调磁电机的模型预测控制

沈赟洁，朱 莉，罗 响，赵继敏

(上海交通大学，上海 200240)

0 引 言

磁性齿轮传动机构是利用两磁极异性相吸、同性相斥的原理来传递力矩的[1]。磁场调制型磁齿轮是一种高性能磁性齿轮结构，在内外磁圈中引入一个由高导磁材料和非导磁材料交错组成的调磁环，内外磁圈产生的磁场经调磁环调制后，两永磁圈磁场的空间谐波数目相互匹配，实现内外转子的转矩及转速传递[2]。磁场调制型磁齿轮的永磁体利用率高、转矩密度大，目前较多文献基于这种调磁原理，提出多种磁齿轮电机[3-5]。文献[4]提出一种调磁电机，该电机在定子上没有永磁体，用电枢代替调制型磁力齿轮外转子，磁齿轮的内转子构成高速转子，调磁环构成低速转子，从而使内外转子同时输出电磁转矩，但该结构的电机磁场相互耦合，内外转子的转矩关系受到三层结构的极对数关系制约，在实际应用中，往往需要内外转子输出任意比例的转矩。文献[10]提出一种对转的双转子调磁电机，在三层调磁电机结构的基础上，增加一套永磁同步电机的结构，从而使内外转子的转矩比例不再受到三层结构极对数关系制约，完成内外转子转矩关系的解耦。目前，针对这种电机的控制策略研究较少。本文通过对该电机的结构原理分析，提出针对该电机的控制方法。通过对电机主副绕组的控制，完成对于两个转子转矩的解耦，使得三层结构间的能量可以自由传递。

模型预测控制(以下简称MPC)是Richalet和Cutler在20世纪70年代提出的一种新的控制策略，并在工业控制领域得到快速应用[6]。随着计算机技术的高速发展，MPC也很快被应用到许多工程领域中。与磁场定向控制(以下简称FOC)相比，MPC替代了电流环的PI控制器，使得控制简单、动态响应快；而与直接转矩控制相比，MPC的转矩脉动小[7]。基于以上的优点，本文将MPC控制原理引入到对转式双转子调磁电机的控制中，实现电机的快速动态响应。

1 电机运行原理分析

同心式磁场调制型磁齿轮的机械结构主要包括：内外磁圈永磁体及其转子轭、调磁环与内外气隙。其运行原理：内外磁圈产生的磁场经调磁环调制后，两永磁圈磁场的空间谐波数目相互匹配，从而达到内外磁圈按一定的传动比运行的目的[8]。当调磁环固定时，可以得出这种磁齿轮的传动比Gr[9]：

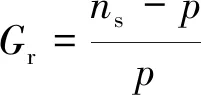
(1)

式中：p为转子极对数；ns为调磁铁块数。

由式(1)可知，磁场调制型磁齿轮使内外磁极产生的磁场经过调制后能与内外磁极相匹配，使内外转子获得相互耦合的转矩。而在实际运行时，往往需要内外转子可以输出任意比例的转矩。本文所研究的对转式双转子调磁电机，在三层调磁电机结构的基础上，增加了一套永磁同步电机结构。可以通过对两套绕组的控制，完成对于两个转子转矩的解耦，使它们可以分别被控制。该电机的设计及磁场分布分析如图1所示。

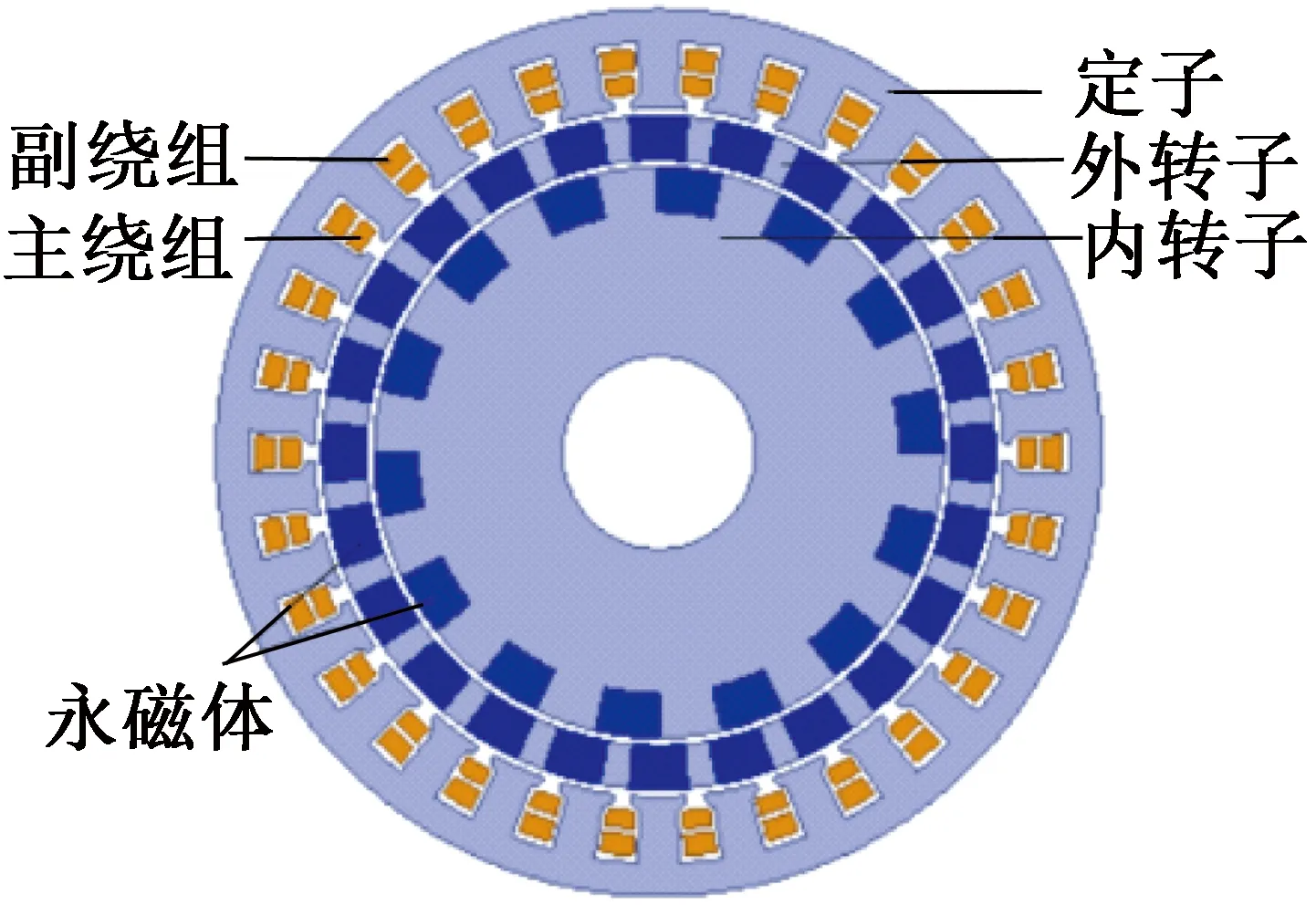
(a) 结构示意图

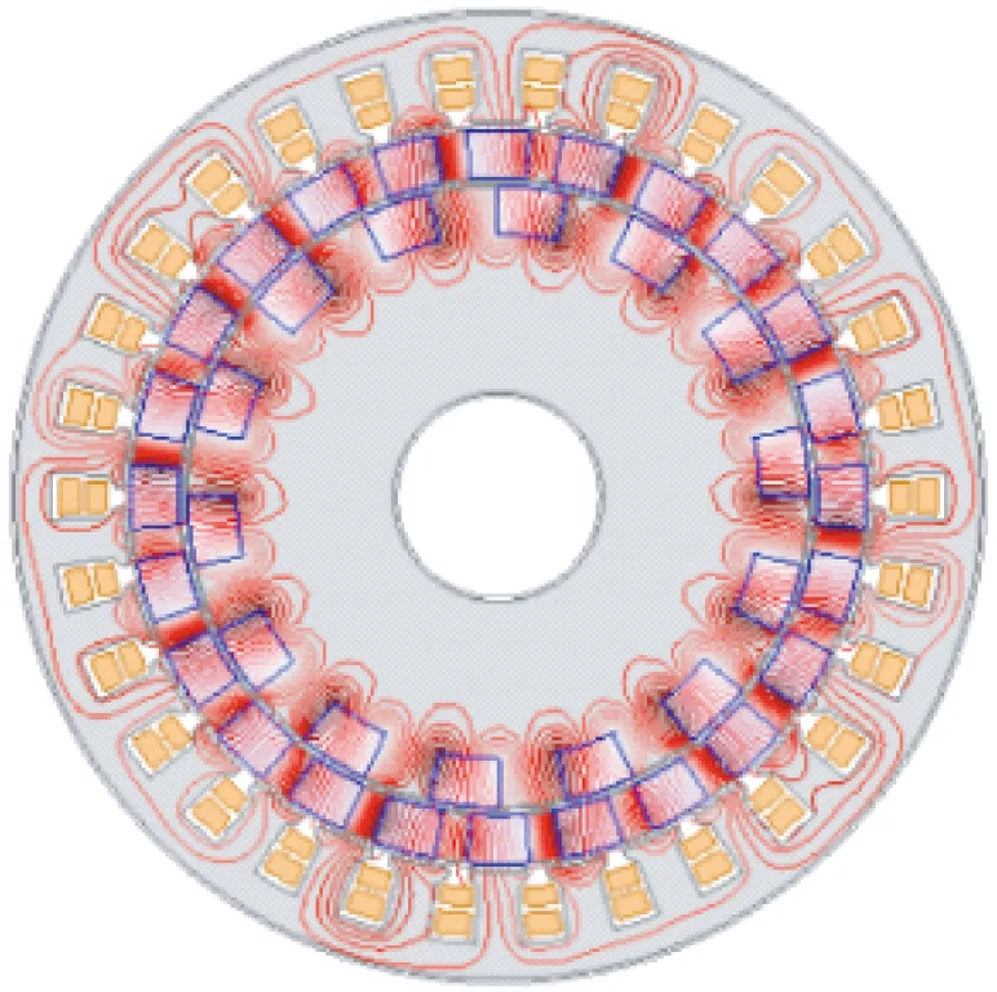
(b) 磁场分布图图1 双转子调磁电机结构与磁场分布图

电机的具体参数如表1所示。

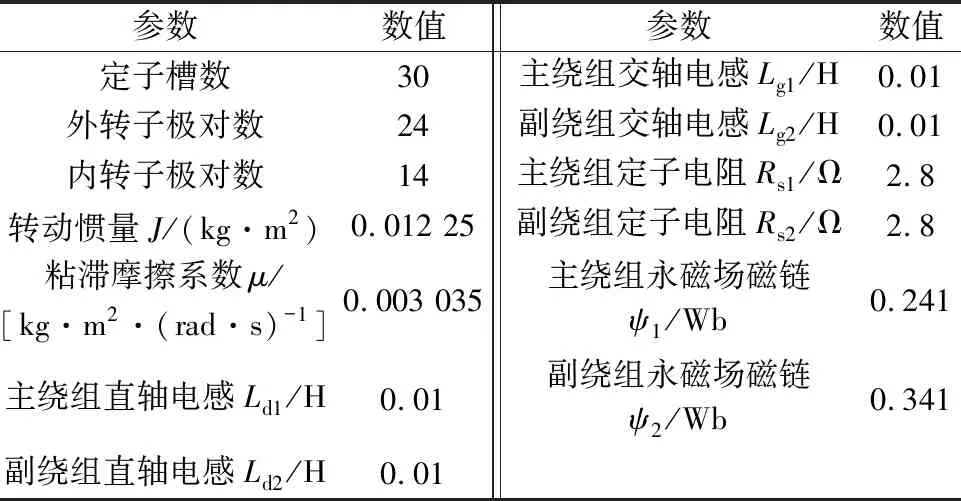
表1 双转子调磁电机设计参数

对于主绕组来说，主绕组与内、外转子构成调磁电机部分，其中外转子24对极，内转子14对极，两转子相对旋转，根据调磁原理，主绕组极对数为10。这样，主绕组、外转子与内转子构成了“定子-调磁铁块-永磁体”与“定子-永磁体-调磁铁块”两套调磁结构，这两套结构均为10-24-14的极对数配比，分别满足调磁原理。在该结构上，另外增加了一组24对极的副绕组，用来与外转子进行单独耦合，这样副绕组与外转子的结构相当于一台永磁同步电机。10对极与24对极的两套绕组均绕在30槽的定子上，共享定子的齿槽结构。

根据磁齿轮与永磁同步电机原理，各层结构的极对数与转速关系：

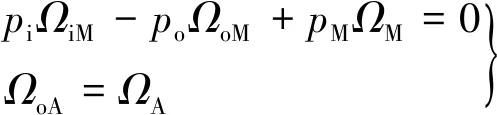
(2)

式中：pi，po，pM与pA分别为内、外转子与主、副绕组的极对数；ΩiM，ΩoM与ΩM分别为主绕组驱动下内、外转子与主绕组的转速；ΩoA与ΩA分别为副绕组驱动下外转子与副绕组的转速。

式(2)给出了主绕组结构的极对数与转速关系，由转速公式Ω=60f/p可得主绕组三层结构的频率关系：

fi-foM+fM=0

(3)

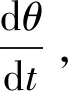
(a) 主绕组结构

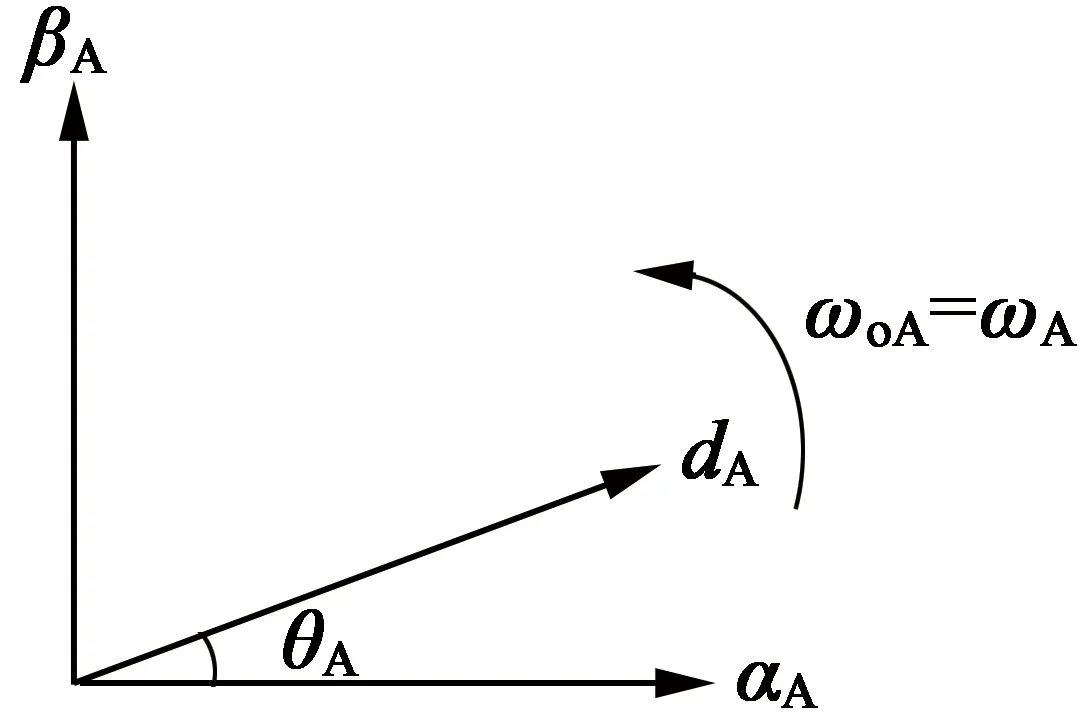
(b) 副绕组结构图2 d-q坐标系下的矢量分布

根据图2可知，在内外转子都以转速为目标进行控制时，外转子转速可以通过副绕组旋转磁场速度确定，即ωo=ωoA=ωA，如图2(b)所示；内转子转速由已经确定的外转子转速及主绕组磁场旋转速度确定，即ωi=ωoM-ωM=ωo-ωM，如图2(a)所示。

在图2(a)中还表征了主绕组磁场与内外转子磁场的相位关系，即式(3)的微分：

θi-θoM+θM=C

(4)

式中：C表征两转子磁链与定子A相绕组(即α轴)之间的夹角，该角度在电机制造时可以调整，同时可以在电机参数辨识时进行测定。

该电机三层结构之间的转矩关系如下：

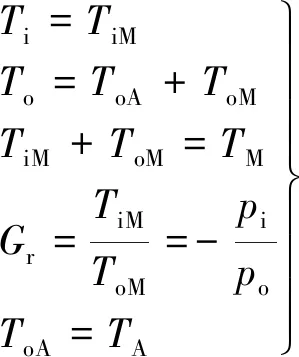
(5)

式中：TiM，ToM与TM分别为主绕组驱动下内、外转子与主绕组的转矩；ToA与TA分别为副绕组驱动下外转子与副绕组的转矩；Gr为主绕组结构的传动比。

由上式可知，在内外转子都以转矩为目标进行控制时，内转子转矩可以通过主绕组电磁转矩确定：Ti=TiM=-TM·pi/(po-pi)；外转子转矩由主副绕组电磁转矩进行合成：To=ToA+ToM=TA+TM·po/(po-pi)。由以上分析可知，与普通调磁电机相比，双转子调磁电机可以通过对两套绕组的控制，实现对内外转子转矩的自由调节。

2 双转子调磁电机的控制

2.1 FOC控制

在d-q坐标轴系统下，永磁同步电机的转矩方程[10]：

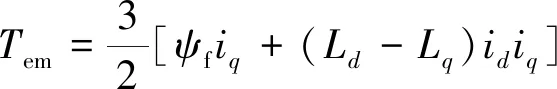
(6)

式中：id，iq为定子电流直轴、交轴分量；Ld，Lq为直轴、交轴电感；ψf为转子永磁磁场。

根据上文对双转子调磁电机的运行原理分析，可得该电机内外转子的转矩方程：

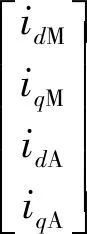
(7)

由式(7)可以看出，该双转子调磁电机的内外转子转矩可以互相解耦。

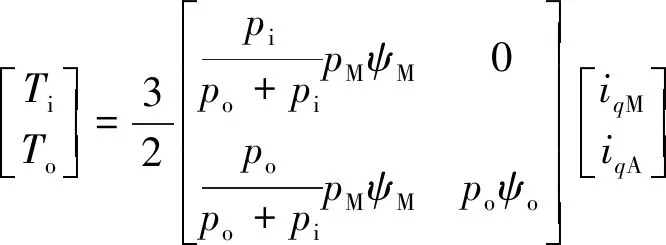
(8)

其控制框图如图3所示。

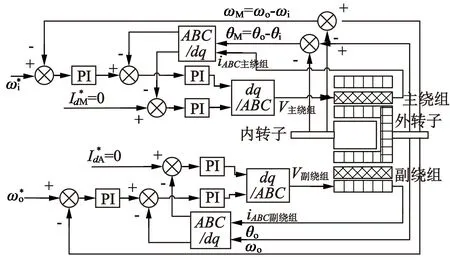
图3 主绕组作为主控制的控制框图

根据式(8)已知，内转子的转矩只由主绕组产生，从而可先以主绕组作为主控制，实现内转子的跟踪，此时由式(5)可见，已在外转子产生一部分电磁转矩，继而通过副绕组控制对外转子转矩进行补偿。图3的控制框图就是以主绕组为主控制展开的电机控制，其具体控制流程如下：主绕组通电产生TM，此时在内转子上产生电磁转矩Ti=TiM=-TM·pi/(po-pi)；以内转子转矩为基础控制目标，对主绕组部分进行PI控制，实现内转子转矩跟踪，即Ti=TLi；此时，外转子上已有部分主绕组产生的电磁转矩ToM=TM·po/(po-pi)；对副绕组部分进行PI控制，补偿ToA(即TA)部分，实现外转子转矩跟踪，即ToM+ToA=TLo。

该双转子调磁电机可以通过对两套绕组的控制，完成对于两个转子转矩的解耦，使它们可以被分别控制。而对于两套绕组的控制顺序没有要求，在具体控制中，也可以副绕组为主控制，主绕组进行跟踪。

2.2 MPC控制

在前一节中，两套绕组均采用FOC控制，尽管稳态响应好，但较多的PI控制器，使得动态响应不可避免地变慢；另外，在仿真实验中也发现副控制部分的PI参数调节较为困难。基于MPC动态响应快的优势，考虑替换副控制部分的控制方式为MPC，使其快速跟踪。

MPC的基本控制原理如下[11]：测量获取当前时刻的电机转速、定子电流等状态量；利用电机数学模型，预测在不同电压矢量作用下的电机转矩与磁链，一般选择两电平逆变器产生的八大电压矢量；确定控制目标，选择使目标函数值最小的电压矢量。图4为MPC与FOC控制框图的对比，与FOC相比，MPC取代了电流环中的PI控制器，使得控制简单、动态响应快。

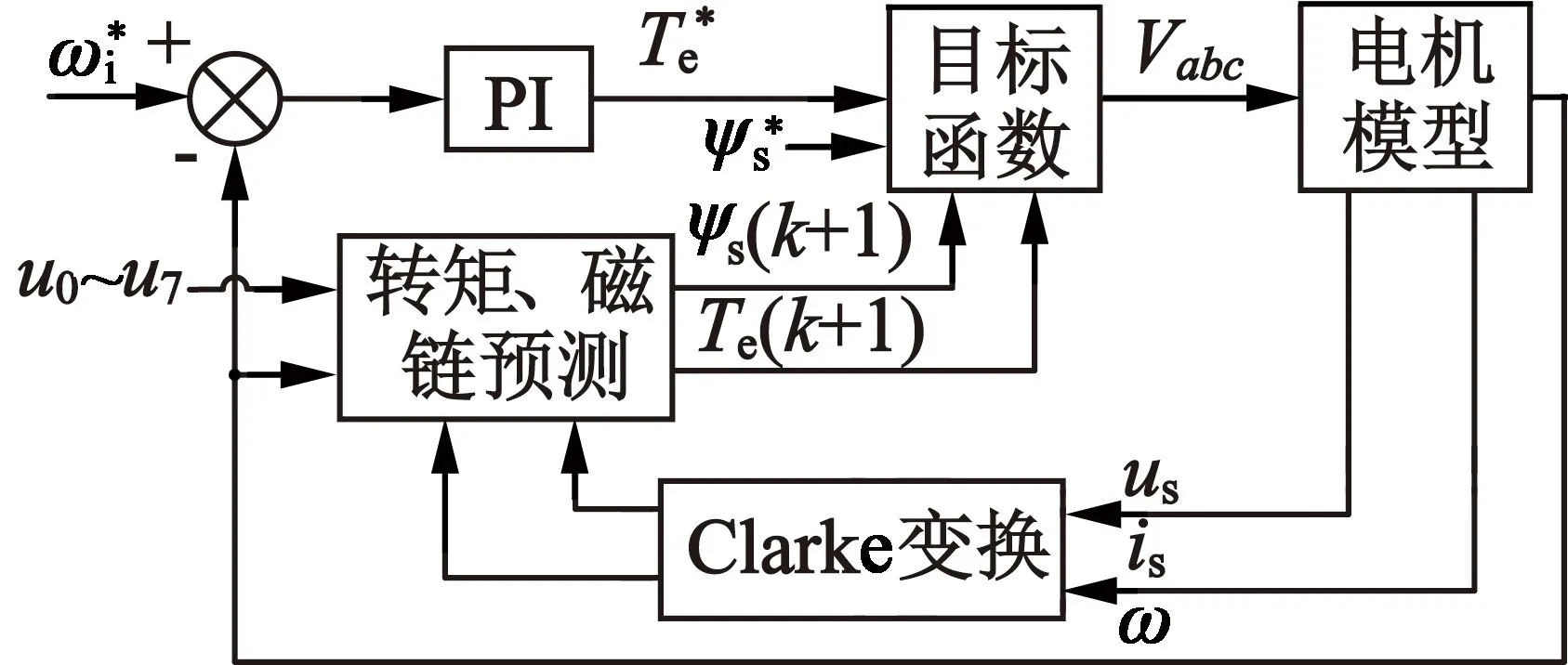
(a) MPC控制框图

(b) FOC控制框图图4 MPC与FOC控制框图的对比

本文的双转子调磁电机分别通过主、副绕组来控制内、外转子，为使副控制部分能够快速跟踪，将其控制方式替换为MPC。以主绕组主控为例，主绕组部分的控制流程与FOC相同，副绕组控制的电流环采用MPC方法快速补偿ToA部分，实现外转子转矩跟踪。控制框图如图5所示。

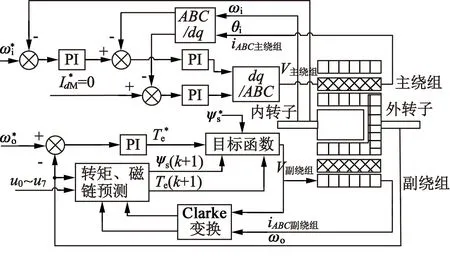
图5 双转子调磁电机MPC控制框图

副绕组与外转子构成一台永磁同步电机，以定子电流is与磁链ψs为状态变量，其在αβ坐标系下的数学模型可表示[12]：

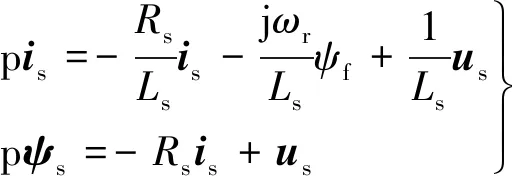
(9)

式中：Rs，Ls为电机定子电阻、电感；us为定子电压矢量；ψf为转子永磁磁场；ωr为电机转速；p为微分算子。

转矩、磁链预测模块采用前向欧拉法对式(9)离散化，具体方程如下：

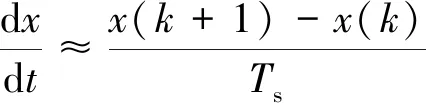
(10)

式中：Ts为系统采样时间；x(k)，x(k+1)分别为k时刻与(k+1)时刻的状态量。

从而，定子电流与磁链在(k+1)时刻的预测值is(k+1)和ψs(k+1)：

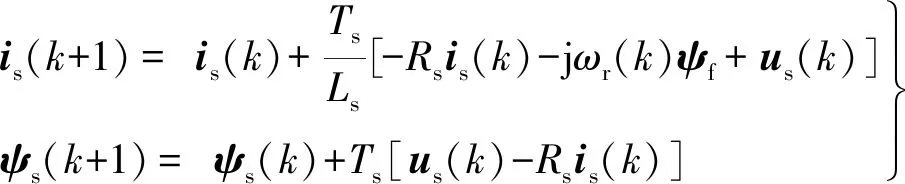
(11)

由式(11)计算得到不同电压矢量作用下定子电流与磁链的预测值，从而可得(k+1)时刻的转矩预测值：

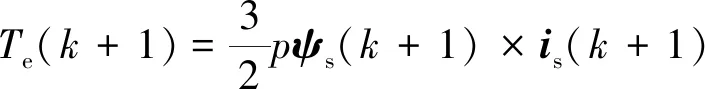
(12)

在矢量选择中，构造如下目标函数：

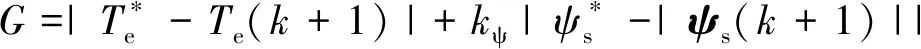
(13)

式中:kψ为权重系数，在控制过程中根据实际情况选取。

由式(11)、式(12)预测在不同电压矢量作用下(k+1)时刻的磁链与转矩，再代入式(13)，选择使目标函数值最小的电压矢量。至于零矢量出现的顺序，根据开关损耗最小的原则来确定，即每次切换开关状态时，只切换一个开关器件。

3 仿真分析

为了验证本文控制算法的有效性，在 MATLAB/Simulink 仿真平台上建立仿真模型。其中电机模型选用表1的参数，仿真时长为0.1 s，采样周期为0.05 ms。仿真时设定内、外转子角速度给定值分别为360 rad/s，500 rad/s，对内、外转子分别施加负载转矩1 N·m，2 N·m。

在主绕组主控时，主绕组部分保持FOC控制，对副绕组部分分别进行FOC与MPC控制，此时外转子在两种控制方法下的转速与转矩响应如图6所示。

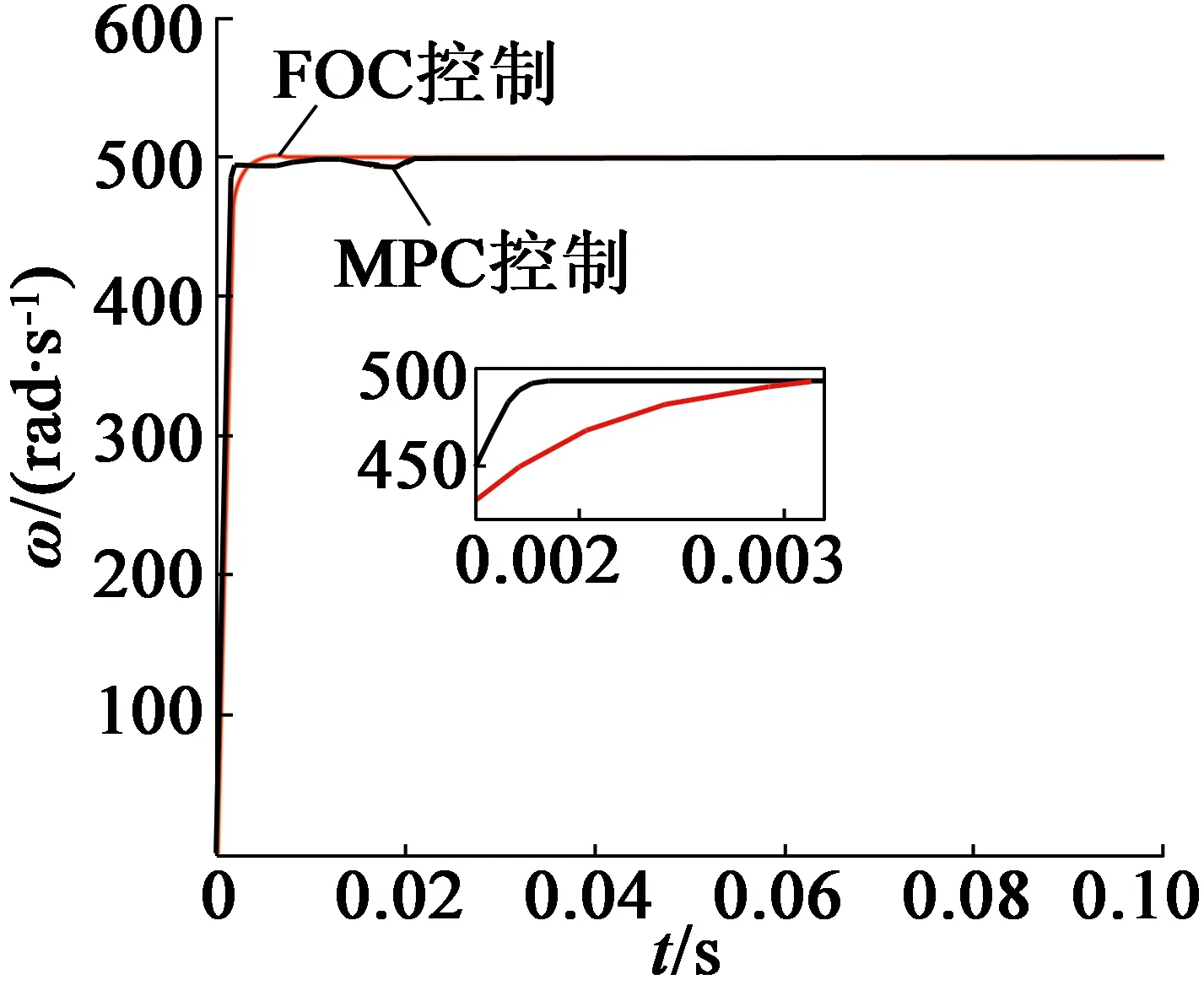
(a) 转速响应

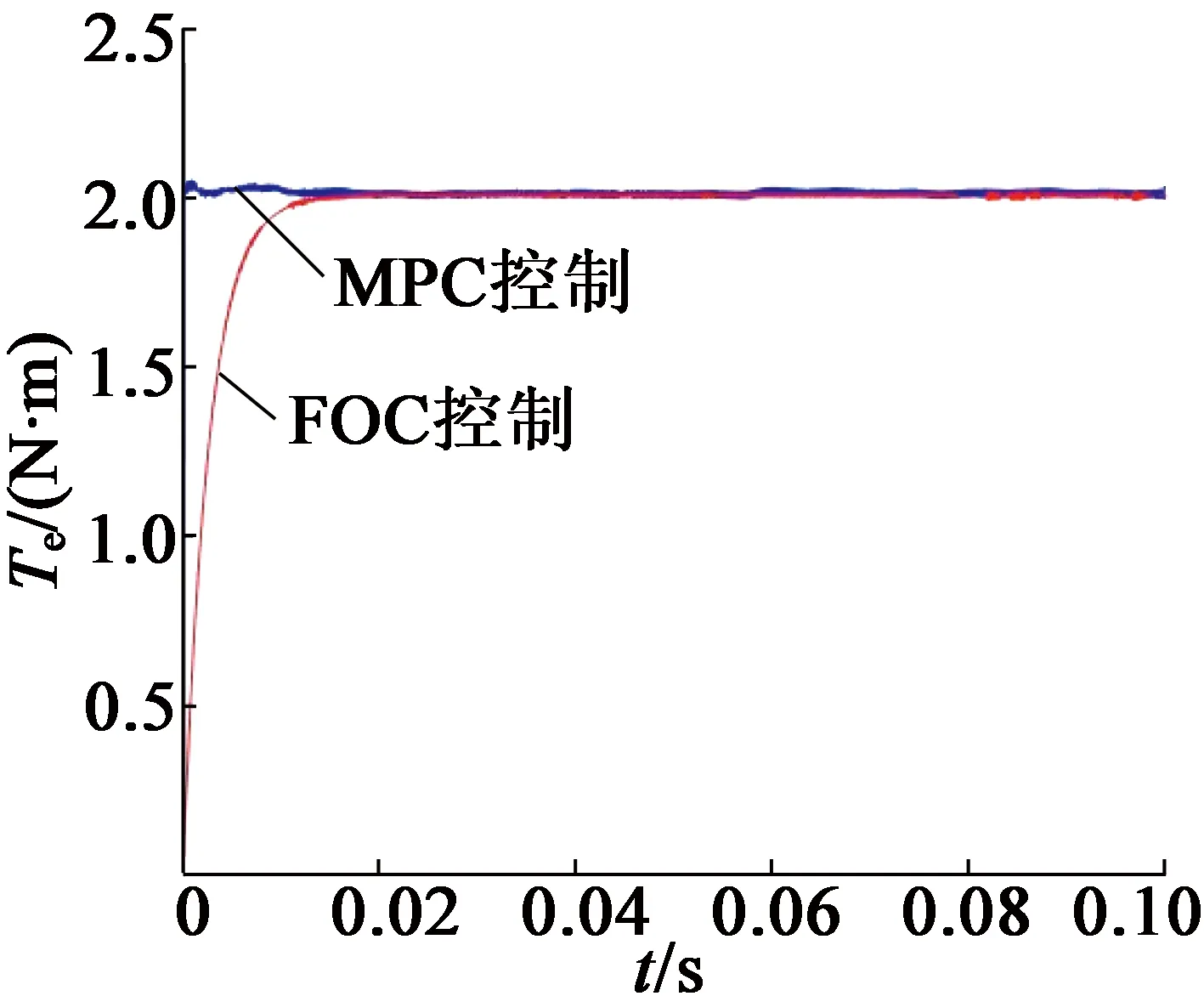
(b) 转矩响应图6 主绕组主控时外转子仿真结果

由图6的仿真结果可以看出，主绕组主控时，将副绕组控制方法替换为MPC，可实现转速与转矩的快速响应。

为验证该双转子调磁电机对于两套绕组的控制顺序没有要求，同样对副绕组主控的控制方法进行仿真分析，即副绕组部分保持FOC控制，对主绕组部分分别进行FOC与MPC控制，此时内转子在两种控制方法下的转速与转矩响应如图7所示。

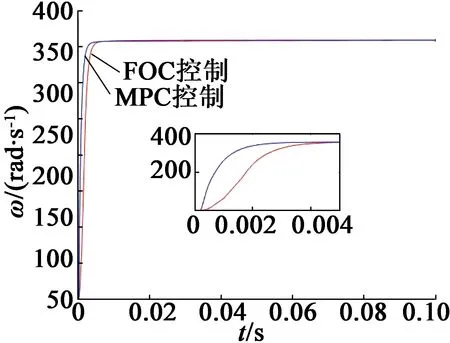
(a) 转速响应

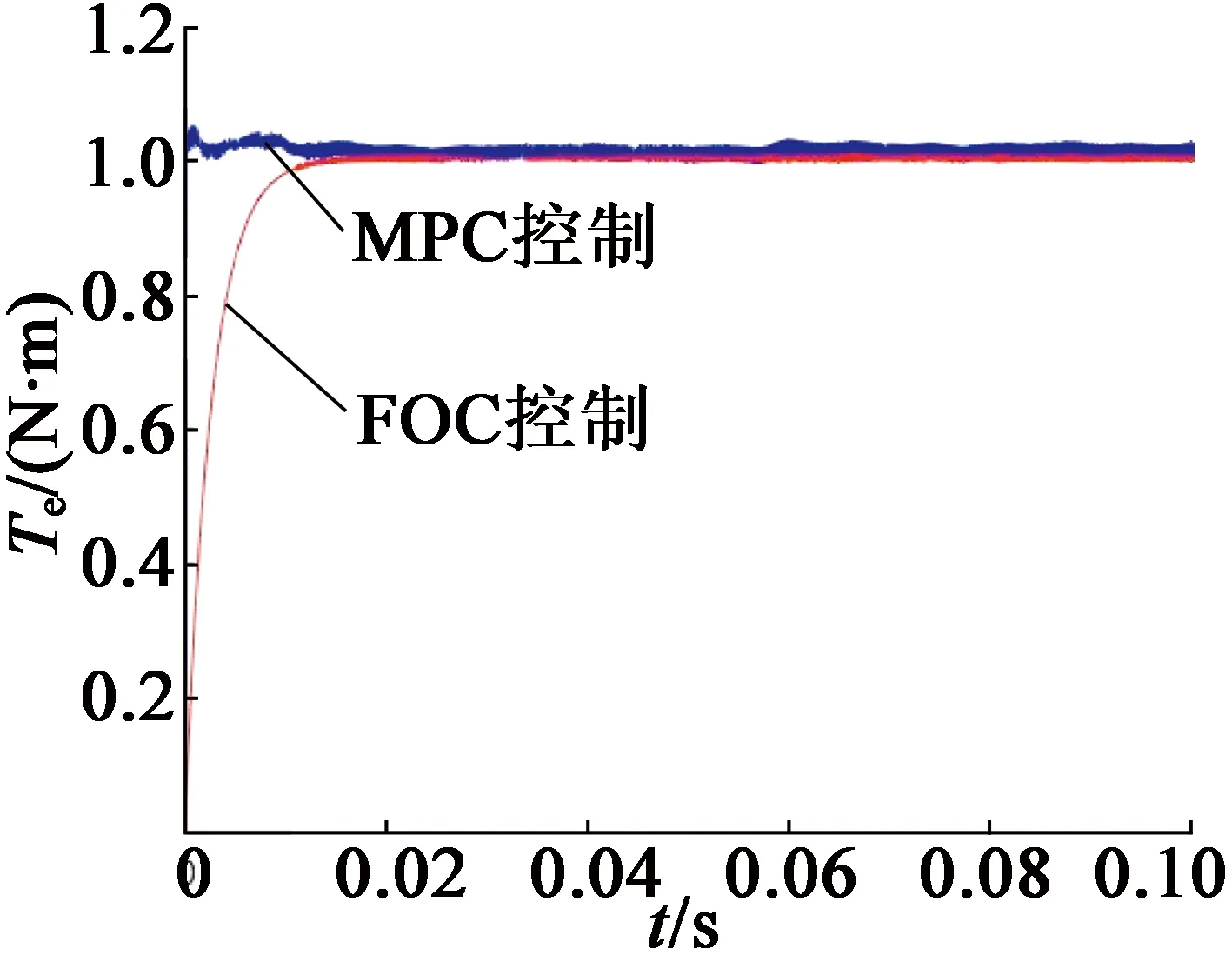
(b) 转矩响应图7 副绕组主控时内转子仿真结果

图7的仿真结果表明，副绕组主控时，将主绕组控制方法替换为MPC，同样可实现转速与转矩的快速响应。

通过上述仿真可以看出，两套绕组的主控制选择并不会影响该双转子调磁电机的运行。电机内、外转子的转矩并非按照极对数关系固定传动，证实该电机可以实现对内外转子的解耦控制。对比MPC和FOC的仿真结果可知，副控制部分采用MPC控制时，其转速和转矩均可快速跟踪给定值。本文的双转子调磁电机的模型预测控制方法是可行的，且相比于FOC控制，其动态响应更快。

4 实验验证

为了验证本文方法的正确性和有效性，使用两台伺服电机作为双转子调磁电机的负载进行测试，实验平台如图8所示。

图8 实验平台

图9为双转子调磁电机实物图，其外转子外径为108 mm，内径为74.7 mm，厚度为16.1 mm，内转子永磁体厚度为15.8 mm，两层气隙厚度均为1 mm，其余设计参数如表1所示。

(a) 电机整体

(b) 定子

(c) 内转子

(d) 外转子图9 电机实物图

电机控制器采用TI公司的TMS320F28335芯片，设计了一套双绕组控制器，用TMS320F28335芯片的两套PWM端口，分别控制主、副绕组。该系统具有两套电流传感器，双转子的位置分别通过两套旋变反馈给旋变控制芯片，并通过SPI通讯给DSP控制器。

在该实验平台下进行转速实验，在主绕组主控时，主绕组控制器采用FOC控制策略，而副绕组控制器分别采用FOC与MPC控制策略，在起动过程中，DSP每隔固定时间间隔记录当前外转子转速，由此得到外转子的转速响应如图10(a)所示。同样地，在副绕组主控时，副绕组控制器采用FOC控制策略，而主绕组控制器分别采用FOC与MPC控制策略，此时内转子在两种控制方法下的转速响应如图10(b)所示。

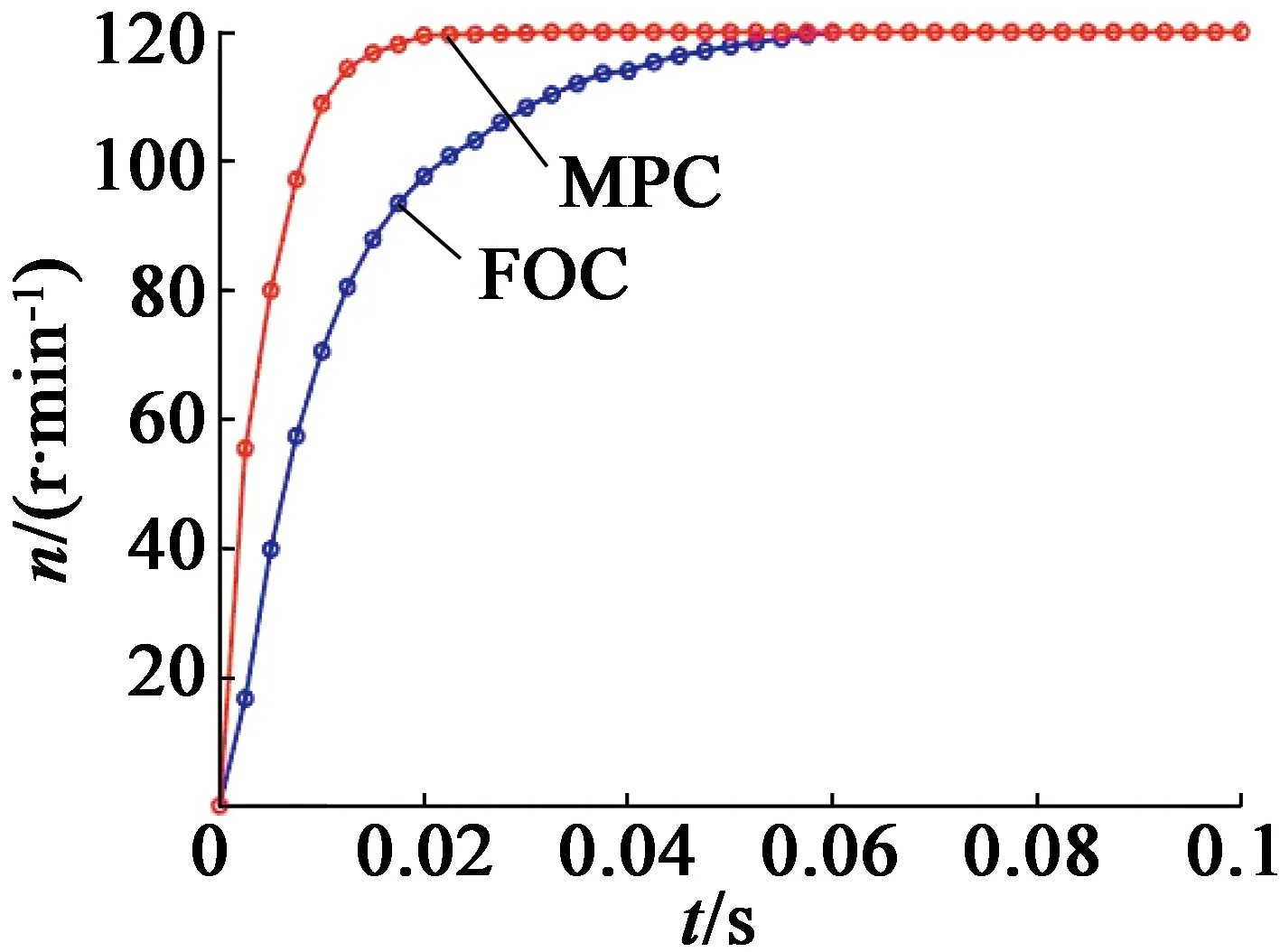
(a) 主绕组主控时 外转子转速响应

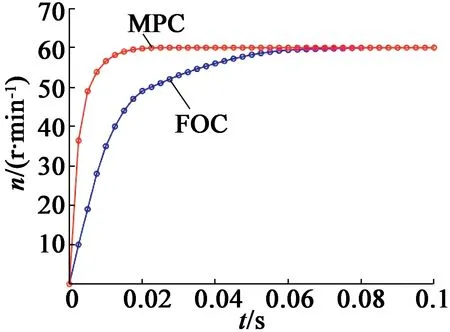
(b) 副绕组主控时 内转子转速响应图10 转速实验结果

由图10的实验结果可知，将绕组控制方法替换为MPC，可实现转速的快速响应，与仿真结果图6、图7的结论一致。

5 结 语

本文在磁齿轮原理的基础上分析了一种对转式双转子调磁电机的结构原理，研究了该电机的控制方法。该双转子调磁电机可以通过对两套绕组的控制，实现对内、外转子转矩的自由调节，且两套绕组的主控制选择对于最终两个转子的转矩、转速解耦控制没有影响。仿真和实验结果表明，双转子调磁电机可以实现对内外转子的解耦控制；将其中一套绕组的控制方式替换为MPC，可加快系统动态响应。