基于改进型滑模观测器的PMSM无传感器控制
2019-11-25叶帅辰姚晓先
叶帅辰,姚晓先
(北京理工大学,北京 100081)
0 引 言
与其他电机相比,永磁同步电机(以下简称PMSM)具有成本低、质量轻、功率密度大、控制可靠性高等优点,被广泛应用于工业设备中的调速及位置精确控制场合。目前,PMSM最为有效的控制方式为矢量控制,而在矢量控制系统中,电机转子位置和速度的精确测量至关重要。常规的测量方法是在电机轴上安装高精度位置传感器,如线性霍尔传感器[1]、光电编码器[2]等。但是这些传感器的使用,会增加电机的质量和加工成本,并且在带有高温、振动和噪声的恶劣工况下,传感器的测试精度会大幅度降低,甚至损坏,进而破坏整个系统的控制可靠性。因此,电机的无传感器控制技术应运而生。近年来,PMSM的无传感器控制技术得到了迅速的发展,并且已成为电力电子系统领域一个重要的研究课题。目前,主流的PMSM无传感器控制方法包括:高频信号注入法[3]、模型参考自适应法[4]、扩展卡尔曼滤波器法[5]和滑模观测器法[6-8]等。其中,滑模观测器法由于具有算法简单、控制可靠性高和工程上易于实现等优点而得到了广泛的应用。
然而,相关文献表明[9-10],在使用传统的滑模观测器对PMSM的转子位置及速度进行估计时,估计结果中会产生大量抖振,进而影响估计精度。抖振的产生主要有以下三个方面的原因:(1)滑模观测器中切换函数的非连续性造成变结构的系统固有抖振;(2)常值的滑模增益会导致在不同转速下系统相对于切换平面的超调或滞后,进而产生抖振;(3)观测器输出的反电动势估计值中带有高次谐波分量,造成转子位置和速度的计算结果中带有抖振误差。
目前,已有较多文献针对抖振的成因做了相关的分析及改进:文献[11]和文献[12]分别利用sat函数和sig函数代替传统的sgn切换函数,用以减小变结构系统的固有切换抖振;文献[13]在传统的滑模观测器中引入模糊控制模块来自适应调节滑模增益,以减小抖振。然而,通过减小观测量中的高次谐波分量来降低抖振的方法在已有文献中却较少涉及。为减小估计结果中的抖振误差并提高估计精度,本文在传统滑模观测器的基础上,引入了串联低通滤波及补偿环节,用以滤除系统估计值中的高次谐波。
1 PMSM矢量控制及数学模型
PMSM转子上安装有永磁体励磁磁钢,定子磁轭上绕有A,B,C三相绕组,当相位差为120°的三相交流电通在绕组上时,会在气隙中产生旋转的定子磁场,进而与永磁体励磁磁场相互作用产生电磁转矩。假设电机磁路不饱和,永磁体励磁磁场和定子磁场在空间中都满足正弦分布,那么在两相旋转d,q坐标系下PMSM的电磁转矩Te可以表示:
Te=p(λdiq-λqid)=p[λfiq+(Ld-Lq)idiq]
(1)
式中:p为磁极对数;λd,λq为直轴、交轴磁链分量;Ld,Lq为直轴、交轴电感;id,iq为直轴、交轴电流;λf为电机磁链。在电机的矢量控制中,为简化控制策略,一般控制id=0,那么电磁转矩可简化:
Te=pλfiq
(2)
通过控制交轴电流iq,在电机磁链已知的情况下,就可以实现对电机转矩的解耦控制。
本文研究表贴式PMSM,其在d,q坐标系下的状态方程:
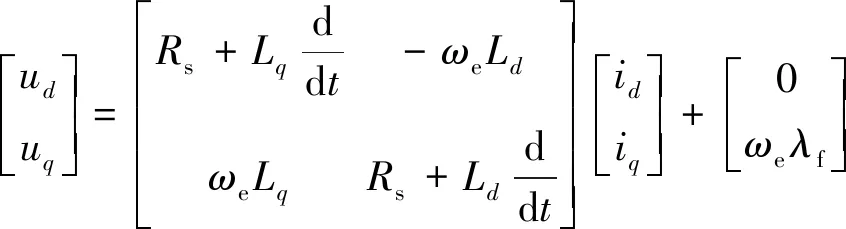
(3)
式中:ud,uq为直轴、交轴电压;Rs为定子绕组电阻;ωe为电机转速。
利用反Park变换,式(3)可转化为电机在两相静止坐标系α,β下的状态方程:
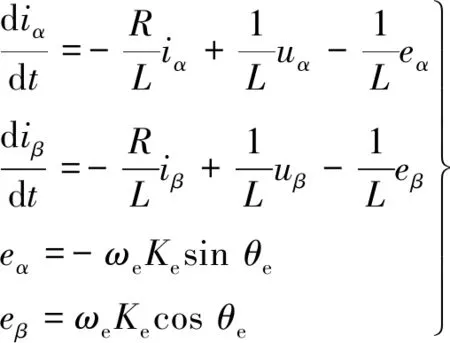
(4)
式中:L=Ld=Lq为定子绕组等效电感;iα,iβ为α轴、β轴电流;uα,uβ为α轴、β轴电压;eα,eβ为α轴、β轴反电动势;θe为电机转子电角度;Ke为反电动势系数。
2 改进型滑模观测器
2.1 传统滑模观测器的构建
对于一个多输入多输出的系统:
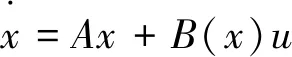
(5)
式中:x∈Rn;u∈Rm;A,B(x)∈Rn×m。
可构造如下的滑模观测器(以下简称SMO),定义滑模面:
s=s(x)=0
(6)
选取控制函数:
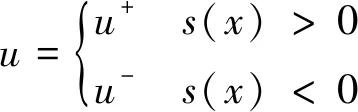
(7)
根据PMSM在两相静止坐标系下的状态方程,构建针对绕组电流的SMO:
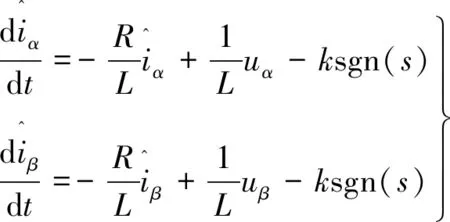
(8)
利用电流估计误差,定义滑模切换超平面:
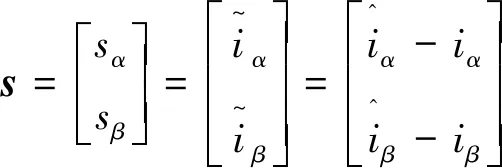
(9)
观测器的切换函数:
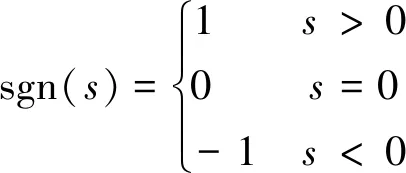
(10)
式中:上标“^”代表观测器的估计值,上标“~”代表观测器的估计误差;k为滑模增益系数。
为证明SMO的稳定性并选取合适的滑模增益,可构建如下的李雅普诺夫函数:
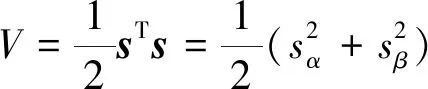
(11)
将式(8)与式(4)的前两个方程作差可得到观测误差s的状态方程:
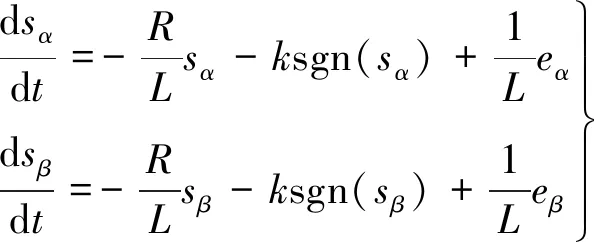
(12)
利用李雅普诺夫稳定性定理,对李雅普诺夫函数求导,并令其小于0,可得:
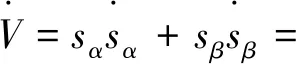
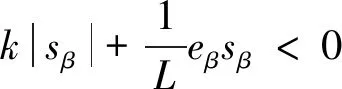
(13)
对式(13)进行进一步缩放,可得:
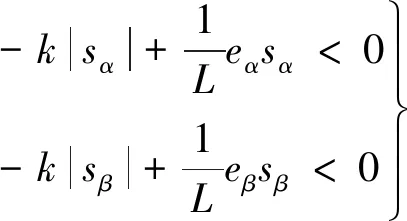
(14)
可以看出,当切换增益满足:
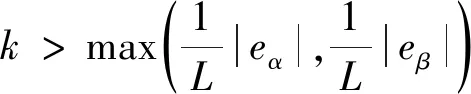
(15)
时,滑模可达性条件满足,SMO可稳定收敛至滑模面。当系统进入滑动模态后,根据式(12)系统的等效控制可写为:
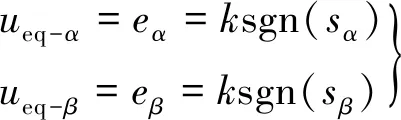
(16)
显然,系统的反电动势信息包含在观测误差的切换开关信号中,再根据式(4)的后两个方程,可得到转子位置及速度的估算公式:
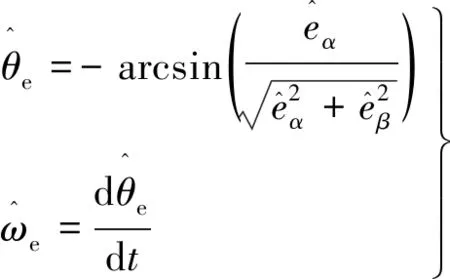
(17)
2.2 串联低通滤波器及其补偿环节
虽然前文所述的传统SMO可以估算PMSM的角位置及角速度,但是受转子两磁极磁钢的安装间隙、逆变器的非线性和气隙磁通空间谐波的影响[10, 14],系统反电动势的估计值中带有高次谐波分量。这些高次谐波分量会被arcsin函数放大,进而在计算角位置和速度的估计值时产生抖振误差,所以,要对反电动势的估计量进行低通滤波。目前,已有相关文献在传统的SMO中引入一阶低通滤波及补偿环节。但实验结果表明,一阶低通滤波器(以下简称LPF)无法完全滤除估计信号中的高次谐波分量,估计结果中依然会存在抖振误差。针对此问题,本文引入了串联低通滤波器(以下简称CLPF),它可以达到一阶低通滤波环节的二倍滤波效果。
CLPF的传递函数:
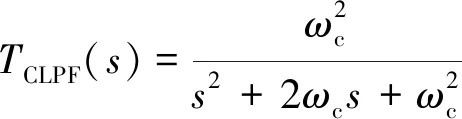
(18)
式中:ωc为串联滤波环节的截止频率。
滤波环节的引入会使系统产生相位延迟,需对其进行补偿,补偿角度:
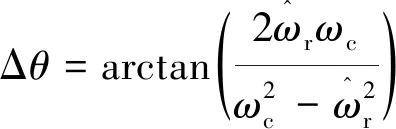
(19)
那么,经过补偿后的转子位置:
引入CLPF及补偿环节的SMO结构框图如图1所示。
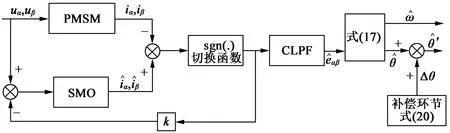
图1 带有CLPF的SMO结构框图
2.3 带有CLPF的SMO性能分析
为证明CLPF的滤波效果,分别利用传统的SMO、带有一阶LPF的SMO和带有CLPF的SMO对反电动势进行估计实验。实验结果如图2所示。
在图2中,图2(a),图2(b),图2(c)表示分别利三种方法估算出的反电动势信号波形,图2(d),图2(e),图2(f)表示三种估计波形的快速傅里叶变换(以下简称FFT)。从图2中可以看出,由于高次谐波的影响,利用不带有任何滤波环节的SMO估计的反电动势信号抖振较为明显,估计误差较大。在引入一阶LPF后,信号的抖振现象有所缓解,但是FFT变换表明,系统中仍有未滤除的高次谐波分量。利用本文的带有CLPF的SMO的信号估计结果最为平滑,大部分的高次谐波分量已被滤除,可大幅提高估计结果的准确性。

(a) 传统SMO
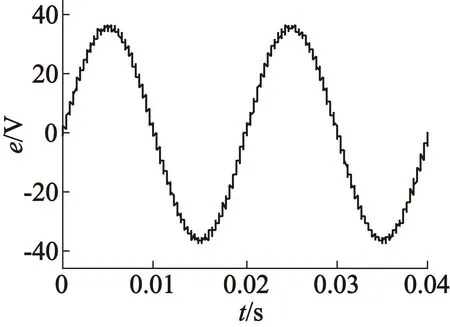
(b) 带有一阶LPF的SMO
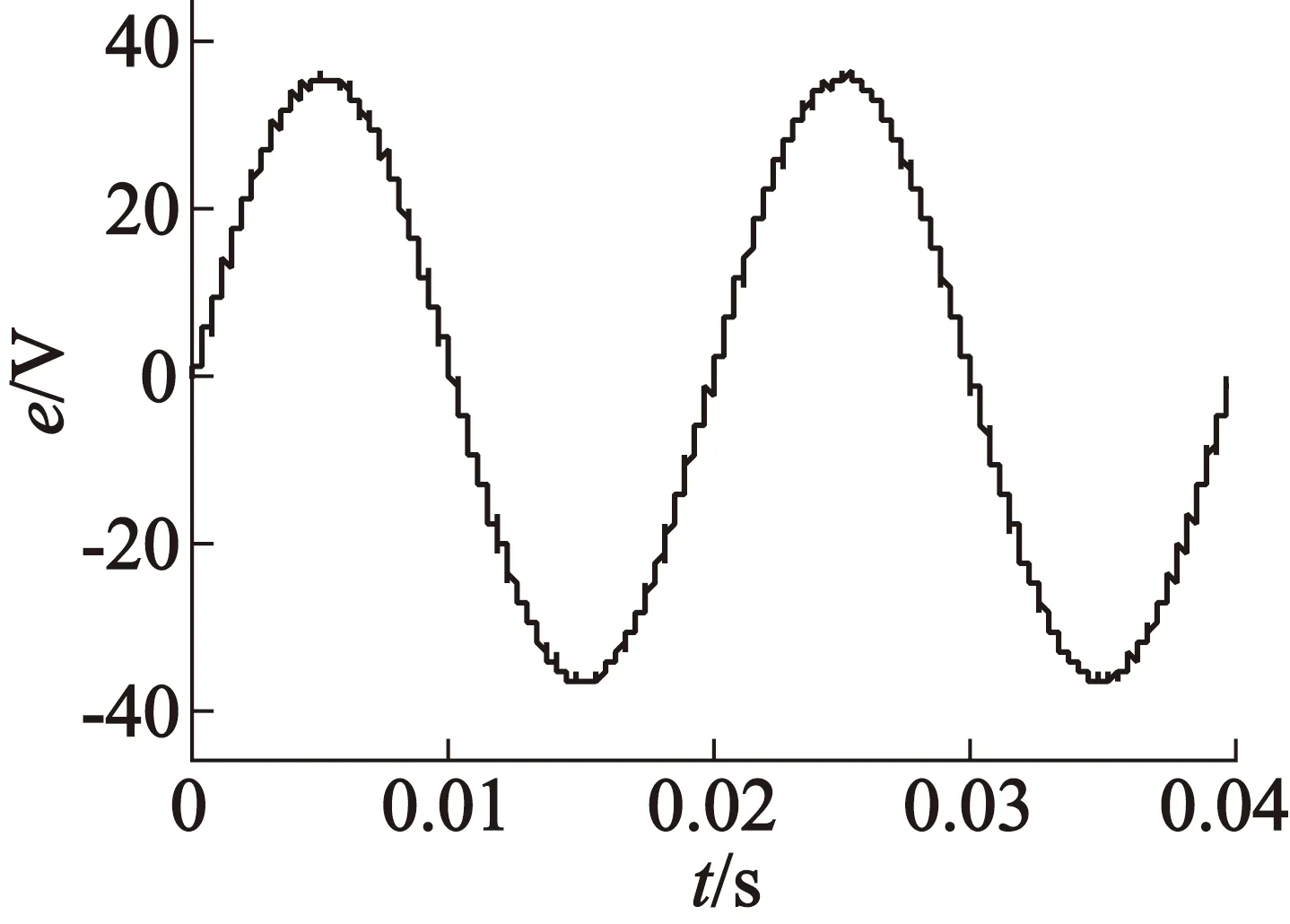
(c) 带有CLPF的SMO
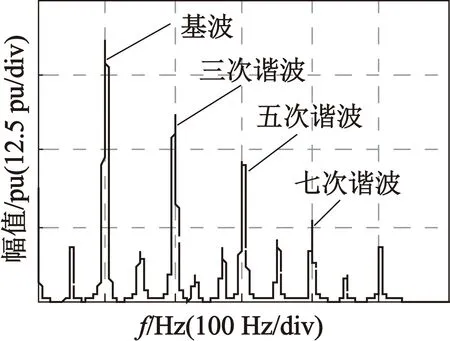
(d) 传统SMO FFT
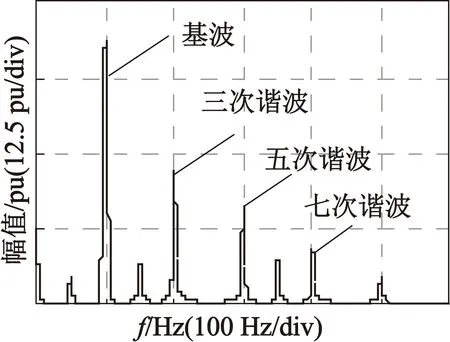
(e) 带有一阶LPF的SMO FFT
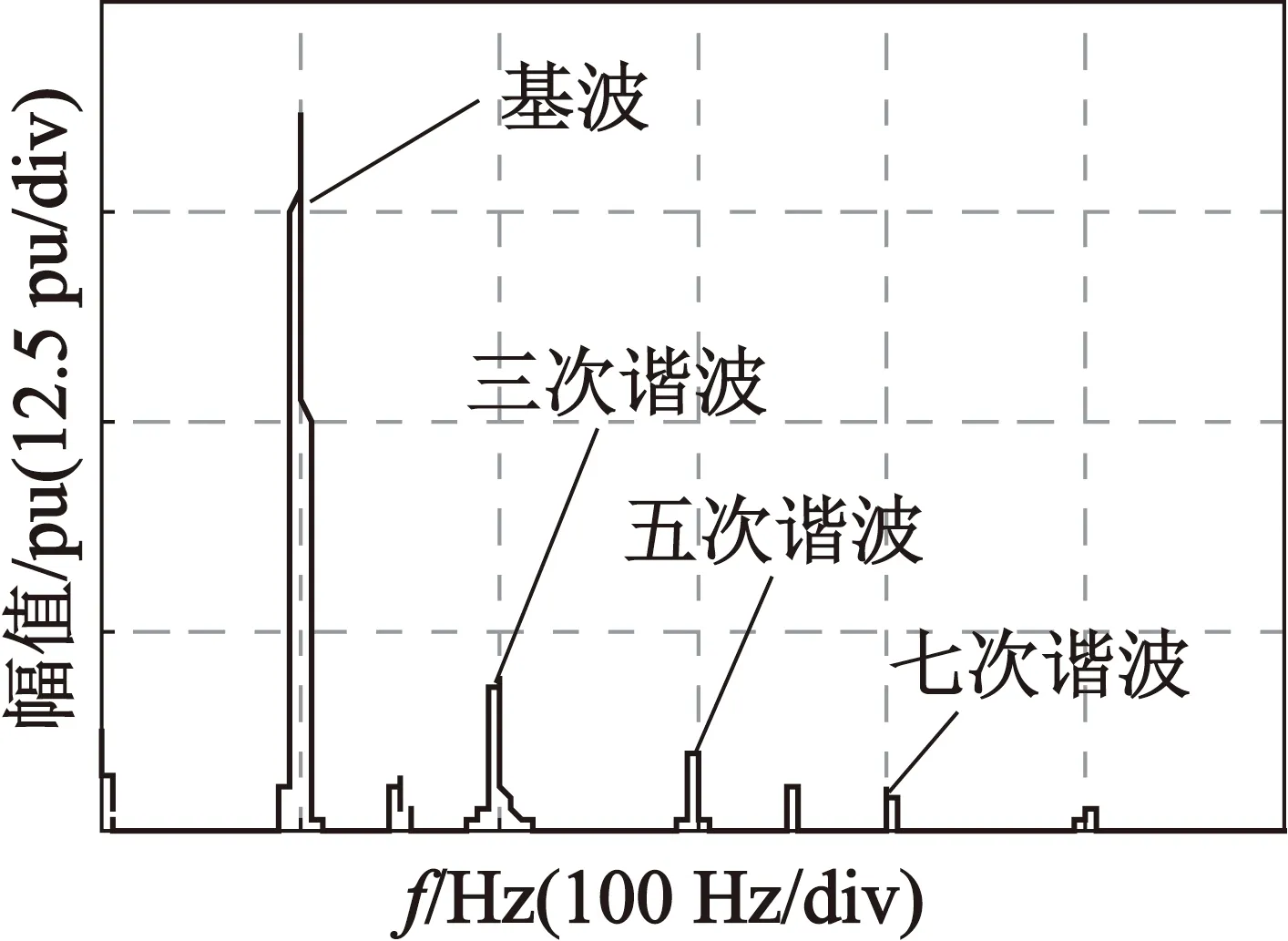
(f) 利用带有CLPF的SMO FFT图2 利用不同方法的反电动势估计结果
3 基于改进型SMO的PMSM无传感器控制系统
为了对带有CLPF的SMO性能进行后续的实验验证,本文搭建了基于这种改进型SMO的PMSM无传感器矢量控制系统。系统整体框图如图3所示。此系统采用速度环和电流环双闭环控制方案,改进的SMO用于估计电机转子的角位置及角速度。
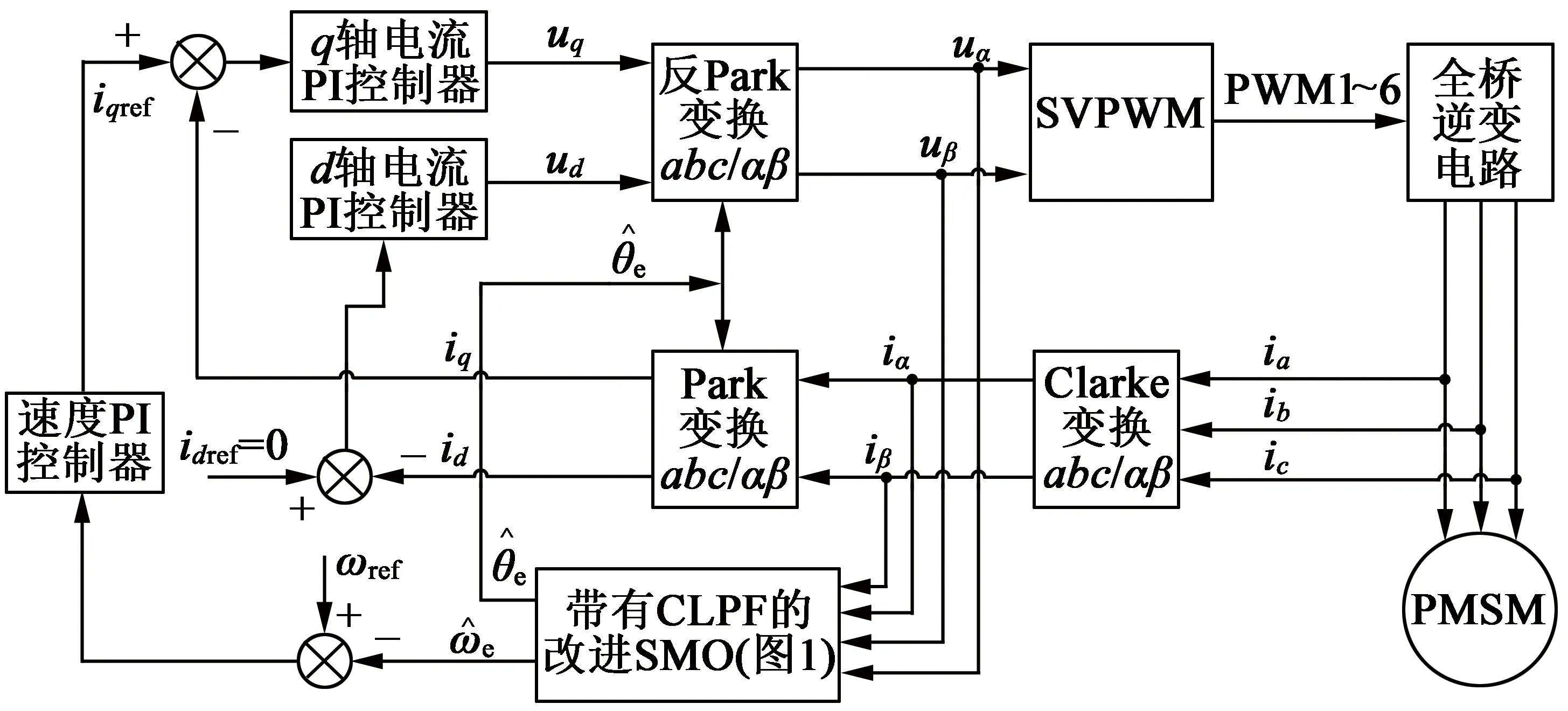
图3 基于改进型SMO的PMSM无传感器控制系统框图
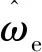
4 实验及结果分析
为验证本文基于带CLPF的SMO无传感器控制系统的控制效果,搭建了以TMS320F28335 DSP为核心的PMSM控制实验平台。实验选用具有如下性能参数的PMSM:极对数为4,额定电压36 V,额定功率400 W,额定转速3 000 r/min,定子电感5.4 mH,电机磁链0.18 Wb。控制系统PI控制器的参数设定:对于电流控制器,Kp=150,Ki=300;对于速度控制器:Kp=0.03,Ki=3。
图4为转速为3 000 r/min时对电机的转子角位置估计结果,图4(a)为参考位置,图4(b)为不带有任何滤波环节的观测器估计结果,图4(c)表示带有一阶LPF的观测器估计结果,图4(d)为带有CLPF的观测器估计结果。图5 表示转速为3 000 r/min时对电机的转子角速度的稳态估计结果,同样,图5(a),图5(b),图5(c),图5(d)分别表示参考转速和利用无滤波器、带有一阶LPF、带有CLPF的观测器估计结果。
(a) 参考位置
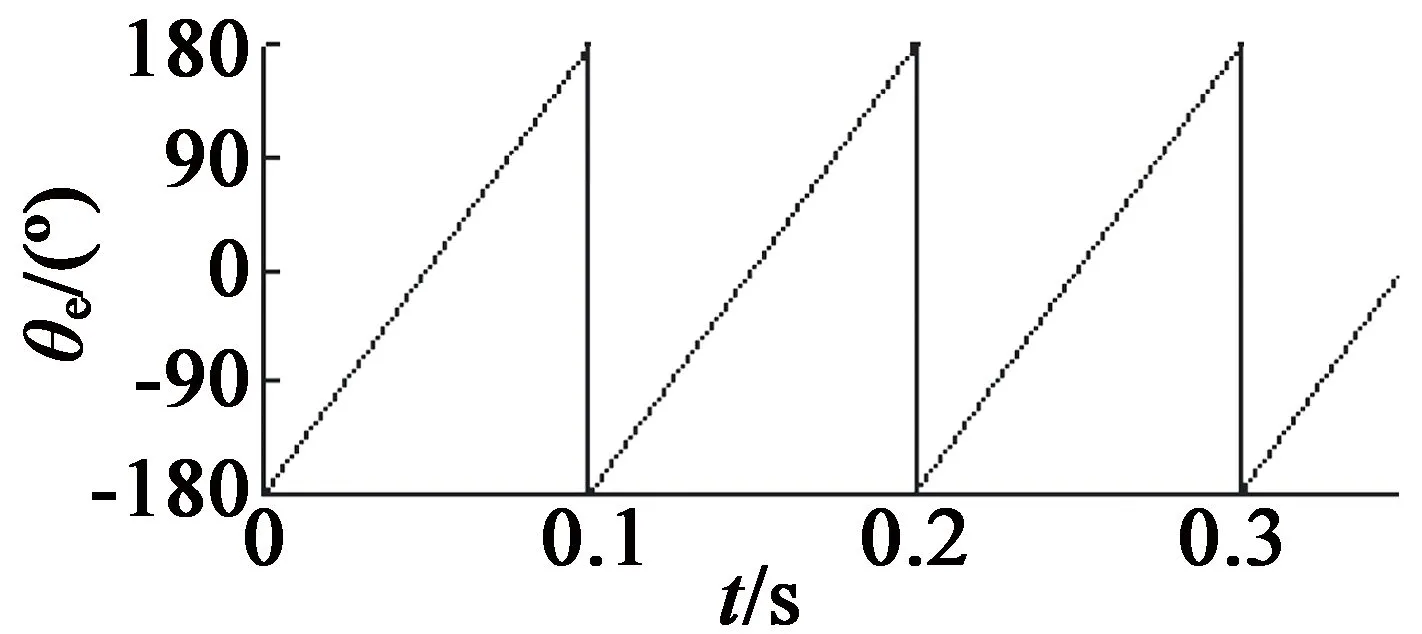
(b) 无滤波环节
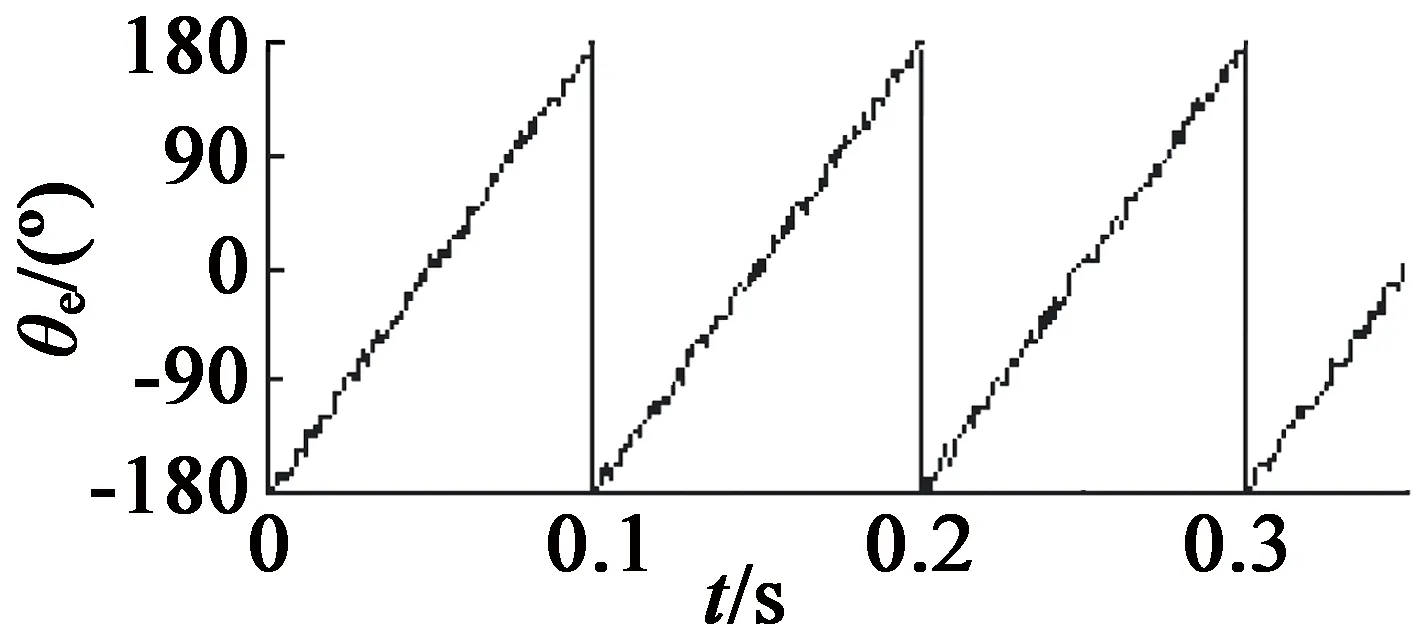
(c) 带有一阶LPF
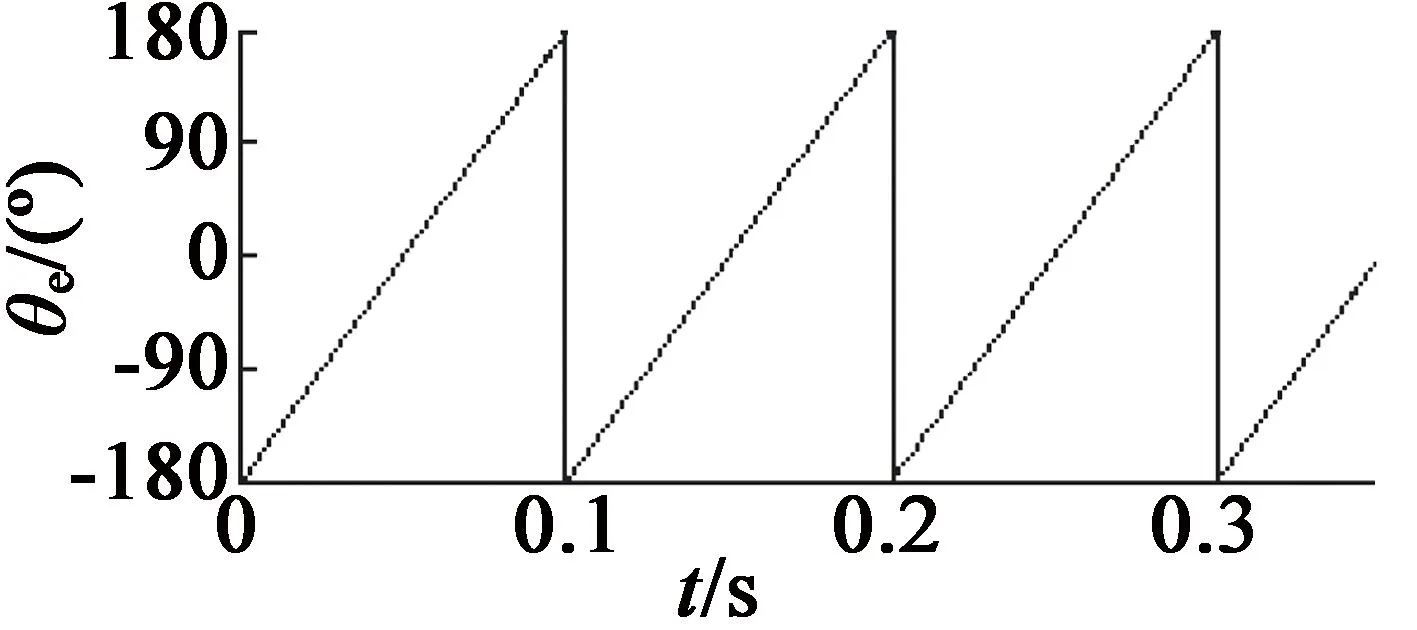
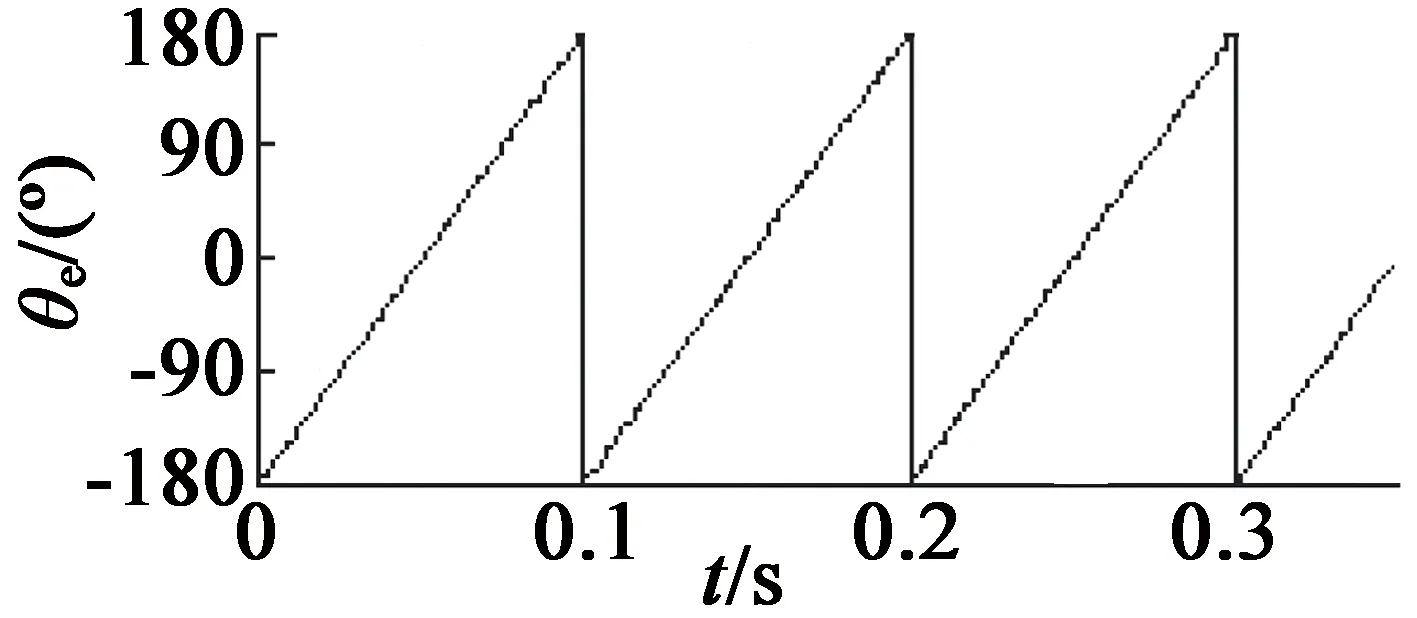
(d) 带有CLPF图4 不同方法的PMSM转子位置估计结果
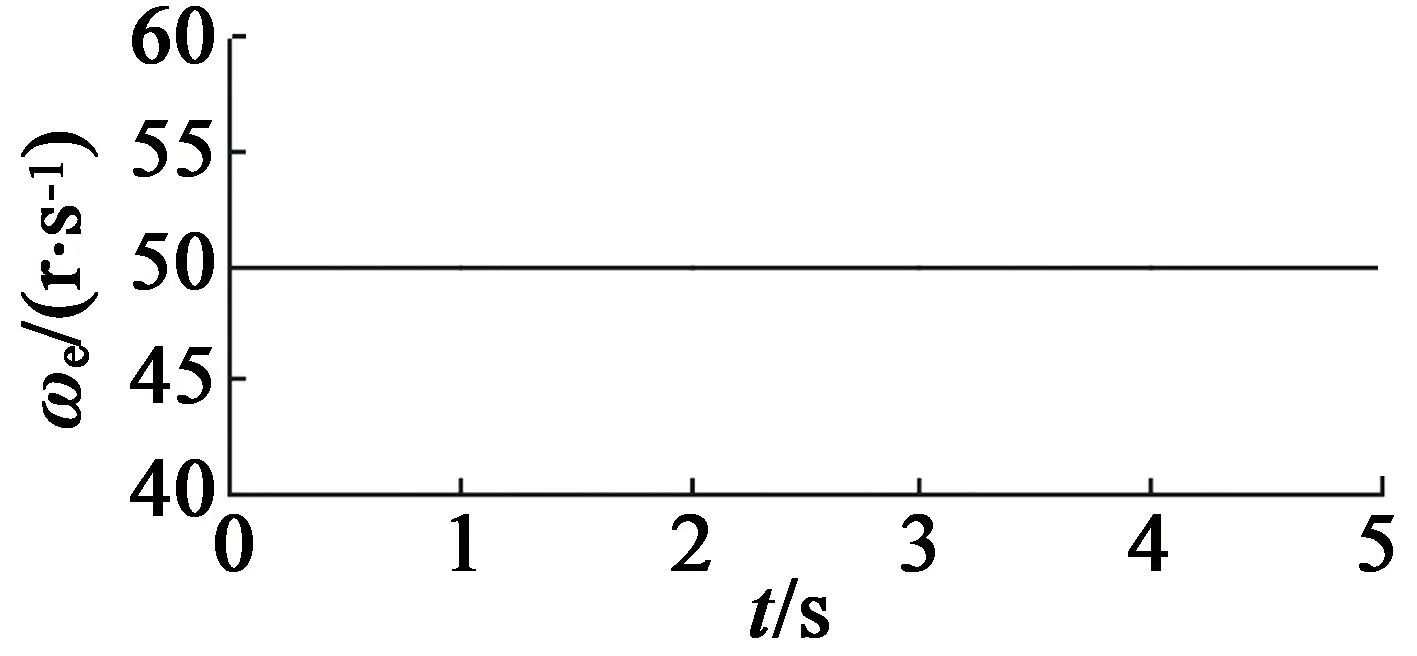
(a) 参考速度
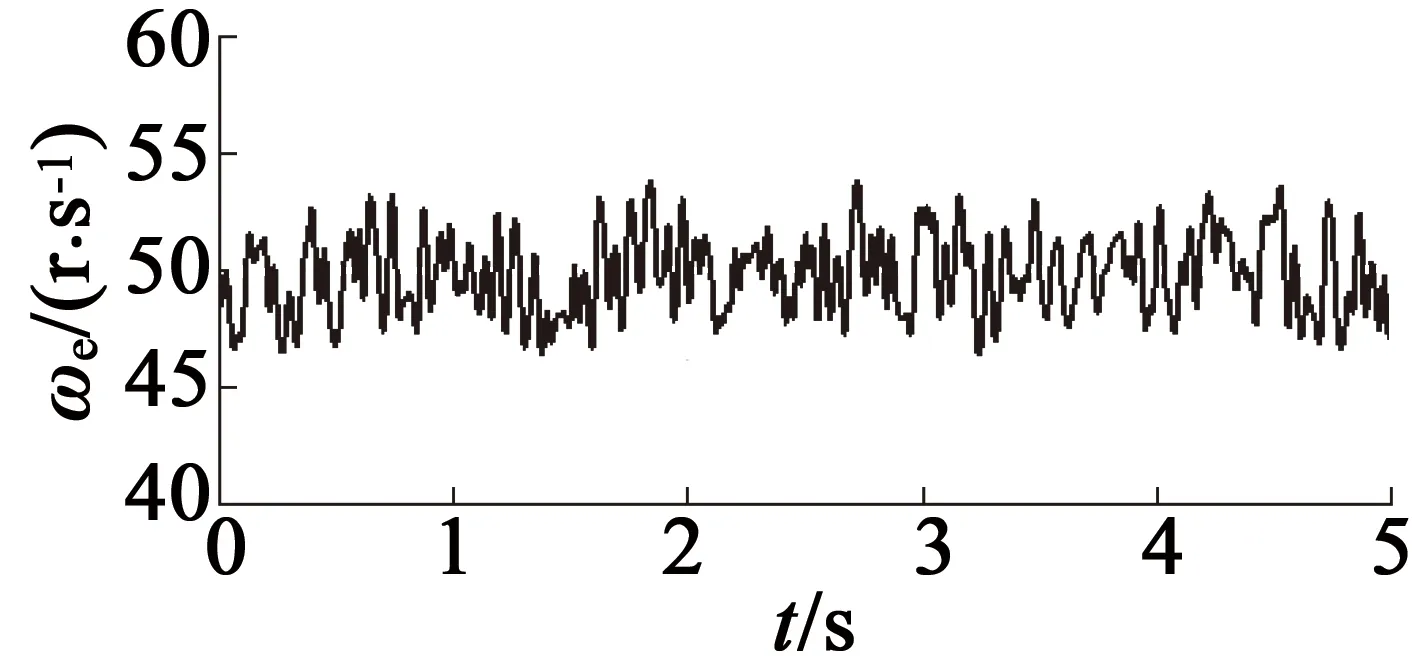
(b) 无滤波环节
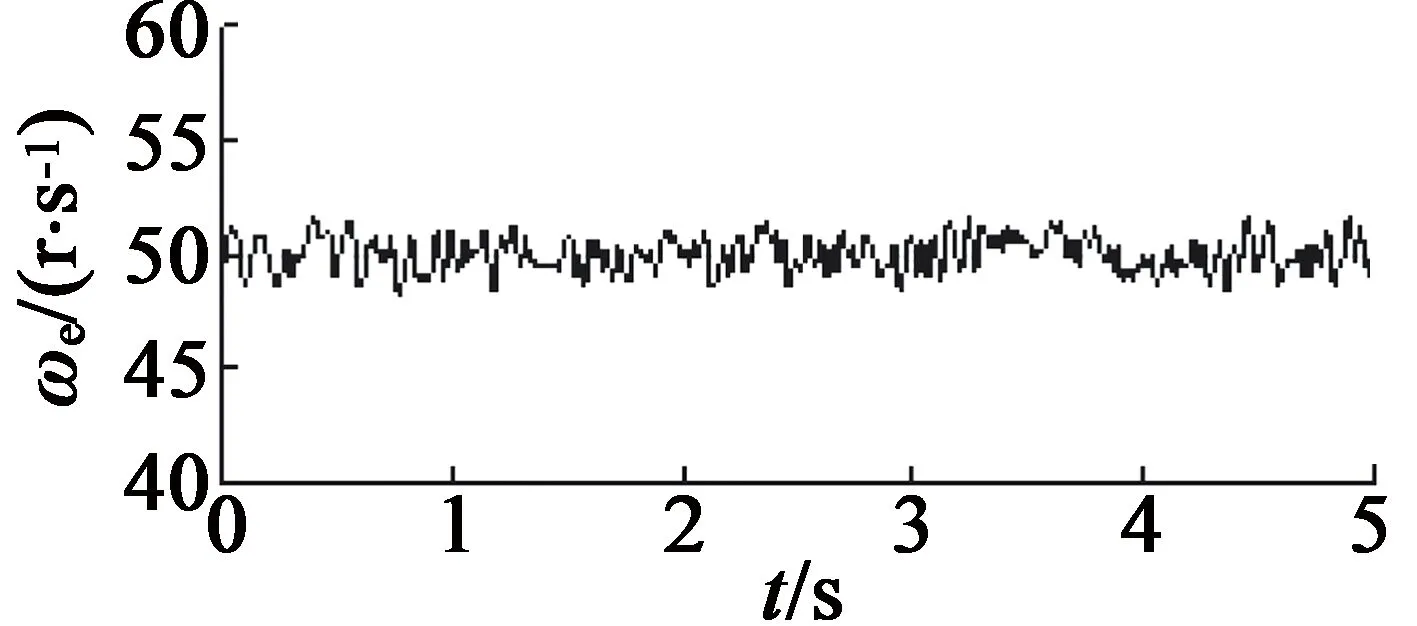
(c) 带有一阶LPF
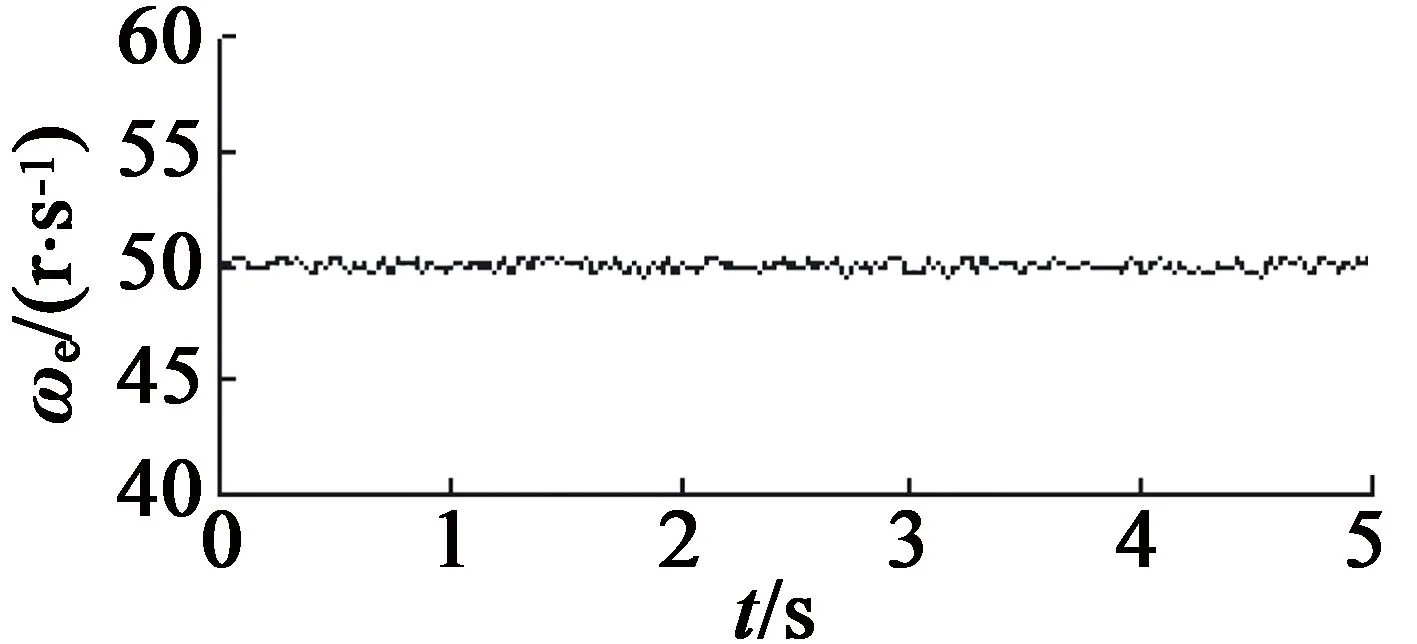
(d) 带有CLPF图5 不同方法的PMSM转子速度估计结果
从图4和图5中可以看出,在对PMSM转子角位置和角速度的估计实验中,无滤波器的SMO估计结果中带有大量抖振,进而导致较大的估计误差,这会严重影响PMSM的无传感器控制系统的控制可靠性。引入一阶LPF后,估计结果中的抖振误差虽然有所改善,但与参考值相比,仍然存在一定的偏差。众所周知,由于DSP具有周期性的工作特性,即使微小的偏差也需要控制系统多个时钟周期的调整时间,这就会影响系统的实时响应速度,从而不利于进行电机的动态控制。而引入CLPF的SMO的估计结果,曲线最为平滑,与参考曲线非常相近,抖振误差得到了大幅降低,从而提高了系统的控制性能。
5 结 语
本文在传统SMO的基础上,引入了CLPF来滤除反电动势估计信号中的高次谐波分量,并构建了基于改进型SMO的PMSM无传感器控制系统,进行
了PMSM角位置及角速度估计实验。实验结果表明,改进型SMO明显滤除了系统中高次谐波,进而减小了估计结果中的抖振误差,提高了估计精度和控制系统的性能,可应用于实际工程。
