数学表达也很关键

朱琴

[摘 要]小学数学教学中，为了将复杂的逻辑讲明白，或者将一些概念揭示清楚，鉴于小学生的理解力和语言表达能力，只能采用通俗易懂、平实无华的语言，但是，简单的口语化表达并不代表在关键处可以含混不清，该咬文嚼字的地方还得咬文嚼字。

[关键词]数学表达; 严谨;轴对称;百分数

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2019）29-0036-02

教师身处教学前沿，听课评课是家常便饭，也是日常必修课。通过听课评课，教师不仅能客观探究教法和教育理念，互相取长补短，而且可以积累真实的教学资料。教学是一门艺术，尤其是小学数学教学，教师的一点小毛病或者失误，都会令课堂教学效果大打折扣，甚至会严重误导学生。本文就两个教学案例，谈谈小学数学教学中教师用语的严密性。

一、轴对称与对称

【案例1】轴对称图形教学片段

师：让我们乘上时光穿梭机，重新回顾什么是轴对称图形。

生1：将图形沿着一条线对折，如果能够完全重合，那么这个图形就是轴对称图形。

师：回答正确，看来这位同学找到了过去的记忆，回答准确无误。

师：请举例说明哪些常见的图形是轴对称图形。

生2：长方形、菱形。

生3：等腰三角形、正三角形。

生4：还有平行四边形。

生5：不对，平行四边形不是对称图形。

师：为什么把平行四边形排除在外？请做出解释。

生5：因为按照轴对称图形的定义，通过操作，发现平行四边形对折后无法与自身重合。

师：这说明“对折后能否重合”是判别一个图形是否是轴对称图形的重要依据。

解析：上述案例中，学生说出了“对称图形”和“重合”两个重点词语，虽然表述不够流畅，但是教师还是给予充分的赞许。然而，教师描述概念时务必要严密，表述准确，不能含糊其辞、模棱两可，更不能存在逻辑语法上的漏洞。难道平行四边形不是中心对称图形吗？平行四边形属于中心对称图形，还是对称的，只是不是轴对称。这节课主讲的是轴对称图形，所以一字之差则天壤之别。涉及重要论断时，切记要逐字逐句推敲，切不可闪烁其词，否则会将命题“平行四边形是对称图形”判错。

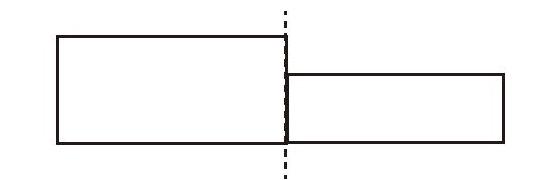
另外，轴对称图形的定义也应该严格陈述为“把一个图形沿某条直线对折后两边完全重合，这样的图形称为轴对称图形”。表述语中的关键词“完全重合”至关重要，不可随意删减，否则就会产生歧义。如下图所示，把该图沿着虚线所在直线对折后左右两边也能重合，只不过是部分重合，没有完全重合，所以严格来说，它不是轴对称图形，因为不满足“完全重合”的要求。概念表述朦胧，造成的直接后果就似是而非。无怪乎总有教師反映，无论怎么强调学生就是无法正确甄别轴对称图形，因为在概念这一源头上就走偏了。

二、百分数

【案例2】百分数练习课

在复习时，教师出示了填空题：“8千克比5千克多（），4毫升比5毫升少（）。”教师点名让两位学生上台演算，并填空，其他学生独立演算。上台演示的两位学生迅速算出结果，但是却给出了截然不同的答案：3千克和20%。预设的答案应该是60%和20%。面对这般结果，师生间进行了如下交流：

师：这两位同学的结果，你们认可吗？（学生中有的支持第一种结果，有的支持第二种结果，有的认为两种结果都正确）

师：这样吧，我们整理一下大家的观点。（经统计，全班60人，有9人赞同第一种结果，有32人赞同第二种结果;教师让大家围绕两种结果展开讨论。）

生1：我觉得两个空都应填写百分数，目的是表示差量占单位“1”的比重。

生2：我反对，就字面意思，题目并未指明要填差量与单位“1”的关系，直接填写差额也说得过去。

生3：第一个空应填差值3千克就行，而第二空应填写差额与标准值的比例20%。

……

（教师选取了几个代表性意见进行分析，同时提供权威解答，发表结论性结语。）

师：这节课的主题是百分数的专项复习，所以要用百分数解决问题。

师：如果全部用百分数解题，答案会是什么呢？

生4：第一个空的结果应该是（8-5）∶5=60%，第二个空的结果应该是（5-4）∶5=20%。

师：非常棒！通过这个练习题，我们巩固了“求一个量比另一个量多（或少）百分之几”的题型和计算方法……

解析：上述案例中，教师为了“推销”自己的观点而误导了学生，最终学生被教师强行洗脑，接受了教师的观点和结论。但是，知识是客观的，“吾爱吾师，吾更爱真理”，求知掺不得半点水分，尤其是数学学科，往往一个关键词或者引导语的失误，或者表述有歧义，就会带来思维混乱。

笔者认为案例中的这道题，本就是低年级比较大小求差值的问题，而并非求百分比的问题。原题的大意应该是：“8千克比5千克多几千克？4毫升比5毫升少几毫升？”若非要按教师的预设来回答，应该对原题做一些改动：“8千克比5千克多百分之几？ 4毫升比5毫升少百分之几？”题面中一定要写明求的是百分比，让要求具体化，其实这也是分数和百分数应用题的解题关键。条件或者问题表述有歧义时，学生往往就会左右为难，难以决断，结果就会出现很大的随意性。

综上可知，当教师授课语言不够精炼时应该及时调整，数学有别于语文，语文里语义相近的词可以互相替代，不影响阅读与理解，但是数学却说一不二，近义词所指代的具体内容会有所差别，容易引起混淆。数学有它的严密性，一个概念往往由几个关键词共同定义，缺一不可。比如，倒数是相互依存的一对数，互为倒数关系的数绝不可以独立存在。再如，对于“同圆或等圆中，圆的半径都相等”，学生往往会忽略前提条件，直接抽取中心信息，得出结论“圆的半径都相等”，从而出错。被忽略的前提条件，正是需要被强调的关键词。教学中，教师要不断通过举一反三，让学生深刻体会到数学表达的严密性，进而重视数学表达。

[ 参 考 文 献 ]

[1] 方代新.多层促“说”，提升学生数学语言表达能力[J].小学教学参考，2019（11）：86-87.

[2] 袁朦朦.学生表达能力在数学教学中的培养途径[J].基础教育论坛，2019（4）：40-41.

[3] 刘桂芳.浅谈低年级计算教学中学生数学语言表达能力的培养[J].新教师，2018（12）：58-59.

（责编 罗 艳）