稀疏正则非凸优化问题之全局收敛分析
2019-11-23储敏
储敏
(武汉大学数学与统计学院, 湖北武汉 430072)
1 引言
近年来, 随着数据量的加大和计算机性能的急速提升, 极大地促进了以机器学习为主导的人工智能技术研究.然而, 当前应用数学家所关心的是如何把实际的问题进行数学上的刻画, 并且求出其显示解或者数值解.以目前最流行的深度神经网络为例, 在训练集上, 我们可以把它归纳为一个非凸非光滑的优化问题[1].同样地, 在矩阵分解以及张量填充中, 其目标函数也是非凸的.另一方面, 由于大数据的高维特性(观测样本量个数小于人们关心的属性的维数), 使得很多传统的数学工具、统计方法不再有效, 对所观测到的大数据本身作更好的先验假设, 则是有效处理大数据的关键.幸运的是, 大多数的实际问题中造成某种结果的影响因素有可能有很多, 但是真正有显著影响的因素实际上很少, 只需要很少的某些属性就能较好的满足于表征我们所关心的这些事物, 反映到数学思想方法上, 稀疏性这个合理的先验假设给处理大数据问题打开了一扇窗.例如, 在图像处理领域, 近些年的发展很大程度上得益于提出:“自然图像可以在某些变换下稀疏表示”这样一个合理的假设[2].又例如, 在日常生活中,一个人的健康指标通常只采用由少数的生物指标来反映.由此, 寻求稀疏解不仅符合问题本身的需求同时也有益于节省存储成本.
考虑如下非凸组合优化问题
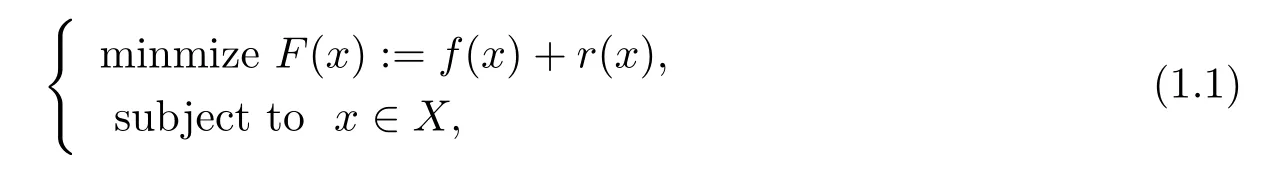
其中X是欧式空间Rd上的凸的紧集,f:X→R是一个光滑非凸函数,r:X→R是一个凸的但非光滑的正则化项.若: 稀疏l1正则化[3], 问题(1.1) 涵盖了一系列非凸组合优化问题.
例1给定一个n维序列(a1,b1),··· ,(an,bn), 其中ai∈Rd,bi∈R, 若令f(x)=其中c是偏差,ϕ是Sigmoid 函数, 即那么问题(1.1) 即化为感知机问题(非凸); 若令在函数f和正则化项r间起到了平衡的作用, 这时问题(1.1) 即为著名的Lasso[3].
2 预备知识
对于实值函数f:X→R∪{+∞},f的定义域domf:=x→X:f(x)<+∞;f为正常函数, 即为闭函数, 即f是下半连续的.
定义2.1[4]给定一个正常函数f:X→R∪{+∞}, 对每个x∈dom(f),f在x处的Frchet 次微分记为f(x), 其定义为
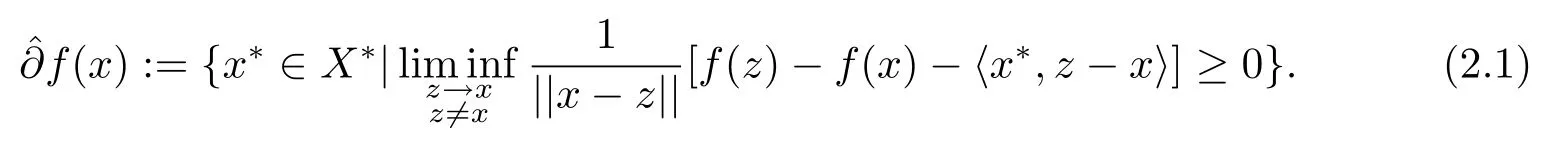
定义2.2[5]给定一个正常函数f:X→R∪{+∞}, 对每个x∈dom(f),f在x处的次微分记为∂f(x), 其定义为

定理2.1[5]令J(x,z) :=H(x,z)+f1(x)+f2(x), 其中f1:X→R∪{+∞} 是一个正常的下半连续的凸函数,f2:X→R∪{+∞} 是一个正常的连续可微函数,H也是连续可微函数.那么∀(x,z)∈X×X, 有
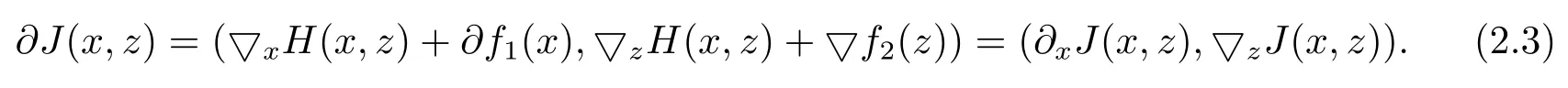
定义2.3[5]f的临界点{x|0 ∈∂f(x)}, 满足的必要非充分条件.
定义2.4[6](KL 函数) (a) 设若存在的某个邻域U, 连续凹函数ϕ:[0,ζ)→R+满足
(i)ϕ(0)=0;
(ii)ϕ在(0,ζ) 上是一阶连续可导的;
(iii) 任意z∈(0,ζ),(z)>0;
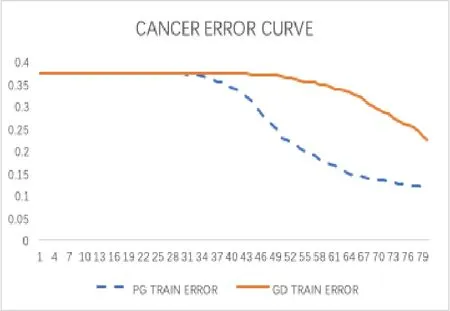
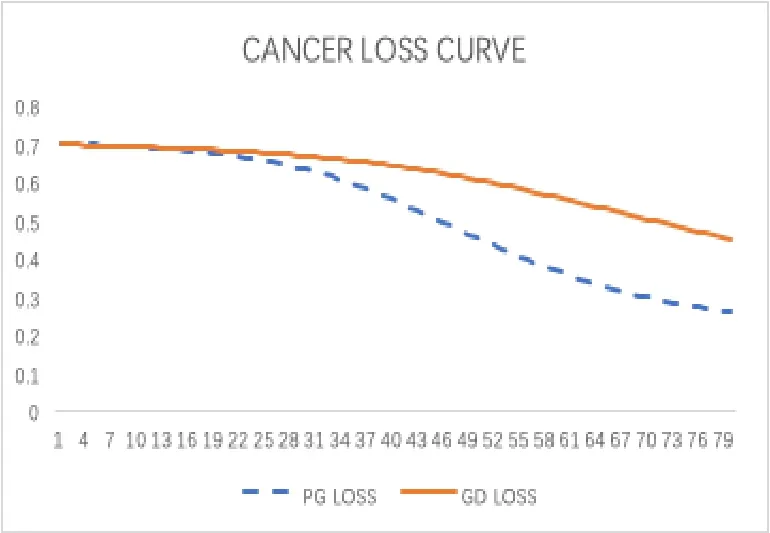
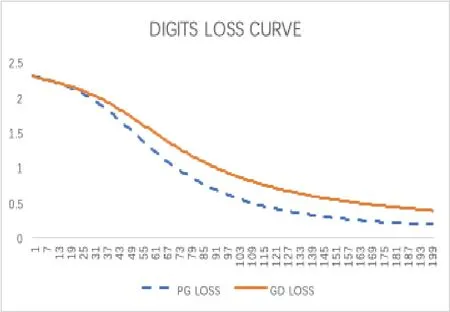
(iv) 任意x∈U∩[f(x) 则称f:Rn→R∪+∞在x∗满足Kurdyka-Lojasiewicz 性质[6]. (b) 在dom∂f内每个点都满足Kurdyka-Lojasiewicz 不等式的正常下半连续函数, 称为KL 函数. 首先, 纵观全文对函数f和g做如下假设. (i)f是Lipschitz 连续可微函数, Lipschitz 常数L> 0, 即∀x,y∈X都有 (ii)f和g是非负、正常、强制、半代数函数. 基于以上假设, 给出如下近端梯度算法[7] 表1: 近端梯度算法 在这个部分, 分析算法1 的收敛性.有必要先对算法1 中的序列{xk} 的特性进行分析. 引理3.1假设(i) 成立且算法1 产生的序列{xk} 满足 (ii) 证(i) 首先定义如下函数 进行化简后可得到 利用f的Lipschitz 连续可微性, 得到 从而(i) 得证. 对于(ii), 将上(3.1) 式两边同时进行求和, 得到 从而(ii) 得证. 对于(iii), 由∂F(x) 的定义, 令 另一方面, 由算法1 的一阶优化条件, 得到 化简得到 由(ii) 中的不等式(3.2), (iii) 得证. 为了证明算法1 的收敛性, 还需要如下定理. 定理3.1[8−10]假设(i) 成立且是算法1 产生的序列, 则{xk}收敛到F的临界点. 证为了证明算法1 的收敛性, 首先要证明以下三个条件. (H1) (充分下降条件)∀k>0, 存在a>0,F(xk)−F(xk+1)≥a||xk+1−xk||2; (H2) (相对误差条件)∀k>0, 存在b>0, 存在使得 (H3) (连续条件)存在子列xki和聚点使得当i→+∞,有xki→且F(xki)→F().事实上, 令a=µ, (H1) 很容易由引理3.1 得出.令易由引理3.1 得出.下面证明(H3). 由F(x) 的强制性, 知道{xk} 包含在水平集{xk∈X:F(xk)≤F(x1)} 中, 利用Bolzano-Weierstrass 定理, 得出存在子集记为xki收敛到某个聚点.由xk+1的定义有 又由Φk的定义, 有由上可得F(xki+1)≤F(). 一方面, 由F的连续性, 得到其中是收敛到的序列, 由引理3.1, 得到{xki+1} 也收敛到.另一方面, 由F(·) 的下半连续性, 得到F(), 于是可以得到: 存在一个子列{xki} 收敛到, 且当得证. 回到算法1 的收敛性证明, 知道F(x) 是半代数的, 且是一个KL 函数, 由KL 函数的性质(见定义2.4), 存在ζ>0,的邻域V和一个连续凹函ϕ:[0,ζ)→R+, 对所有的x∈V, 有 其中F∗:=F(). 取r>0, 则Br()⊆V.已知存在子列{xki} 收敛到, 则意味着存在一个xkN, 使得 (a)xkN∈V; 通过(H1), (H2), (H3), (a), (b) 和(c), 利用文献[10]的定理2.9, 可以得到{xk} 收敛到. 考虑(1.1) 优化问题, 我们通过设计加L1,L2 正则化项的神经网络做分类试验, 来验证算法的有效性. 神经网络[11]的模型如图1 所示, 一个神经元对输入信号X=[x1,x2,...,xn]的输出为y=f(u+b), 其中公式中各字符含义如图1 所示.神经网络的训练通常用误差函数(也称目标函数)E来衡量, 当误差函数小于设定的值时即停止神经网络的训练.误差函数为衡量实际输出向量Yk与期望向量Tk误差大小的函数, 常采用二乘误差函数来定义为为训练样本个数.在模型训练时, 如果参数过多, 模型过于复杂, 容易造成过拟合(overfit), 即模型在训练样本数据上表现得很好, 但在实际测试样本上表现得较差, 不具备良好的泛化能力.为了避免过拟合, 最常用的一种方法是使用使用正则化, 例如L1 和L2 正则化, 其中L1 正则化产生更加稀疏的权值.在误差函数的基础上加正则化项后的损失函数为 图1: 人工神经元模型 表2: L1+ 近端梯度下降算法与L2+ 梯度下降算法分类错误率 在不同数据集上, 采用L1+PG 和L2+GD 的模型进行神经网络训练, 可以看到L1+PG 模型的分类错误率均低于L2+GD 模型, 通过损失曲线的对比, 可以看出L1+PG 比L2+GD模型的训练更加快速达到收敛. 图2: CANCER 数据集上的错误率曲线 图3: DIGITS 数据集上的错误率曲线 图4: CANCER 数据集上的损失曲线 图5: DIGITS 数据集上的损失曲线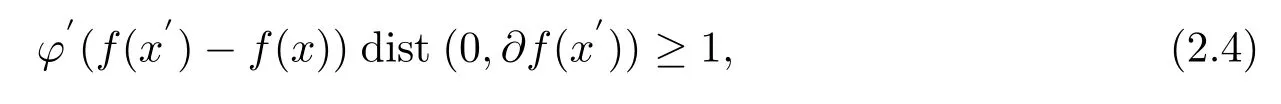
3 模型及收敛性分析



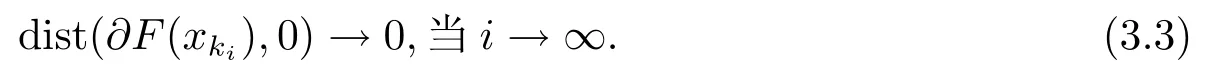

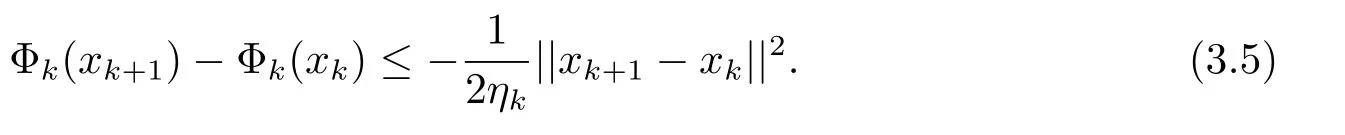


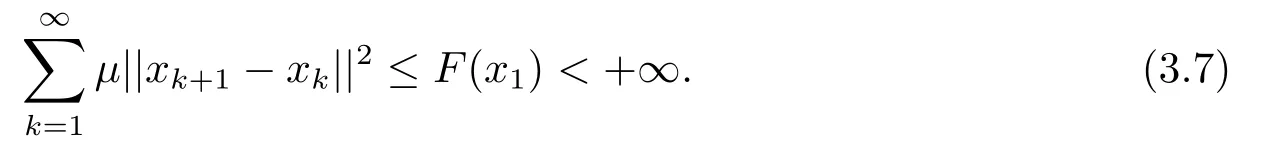
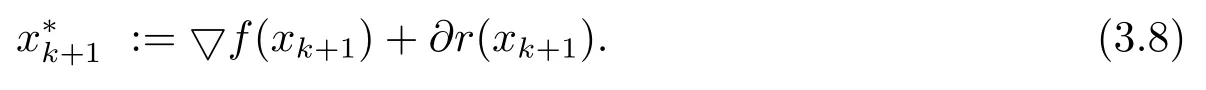

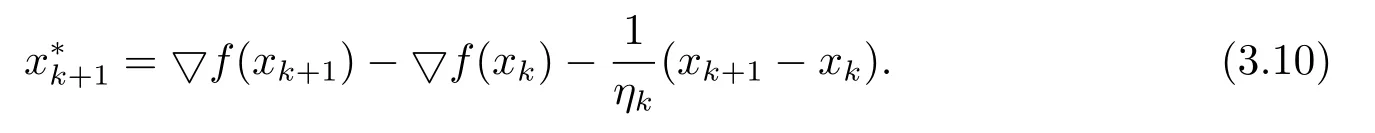


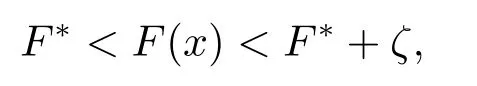
4 数值试验