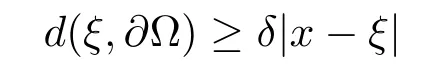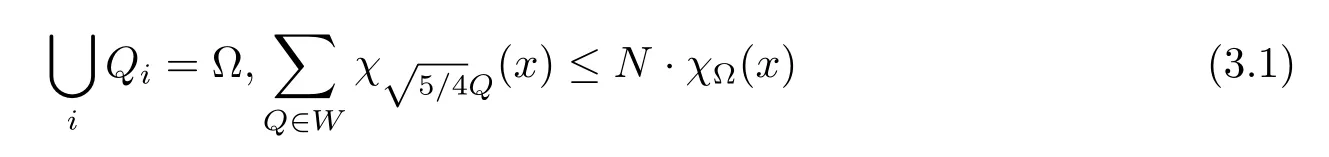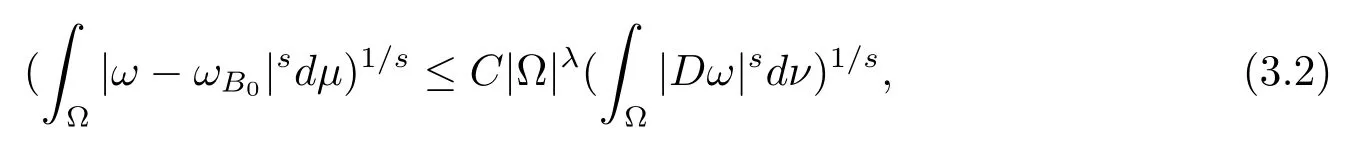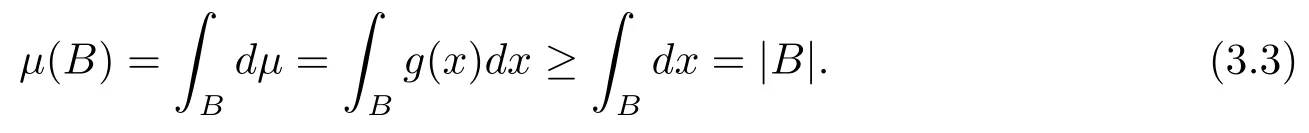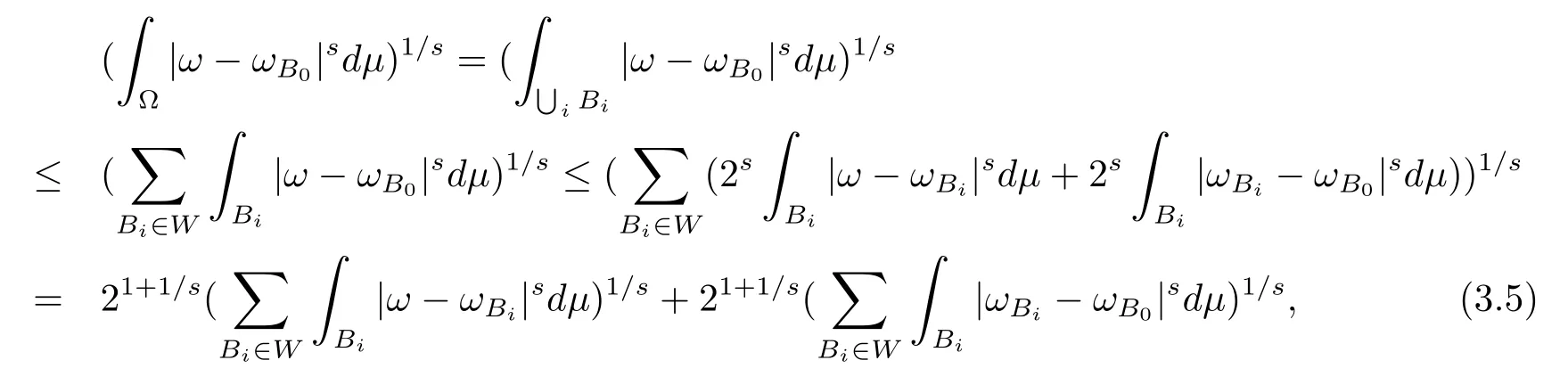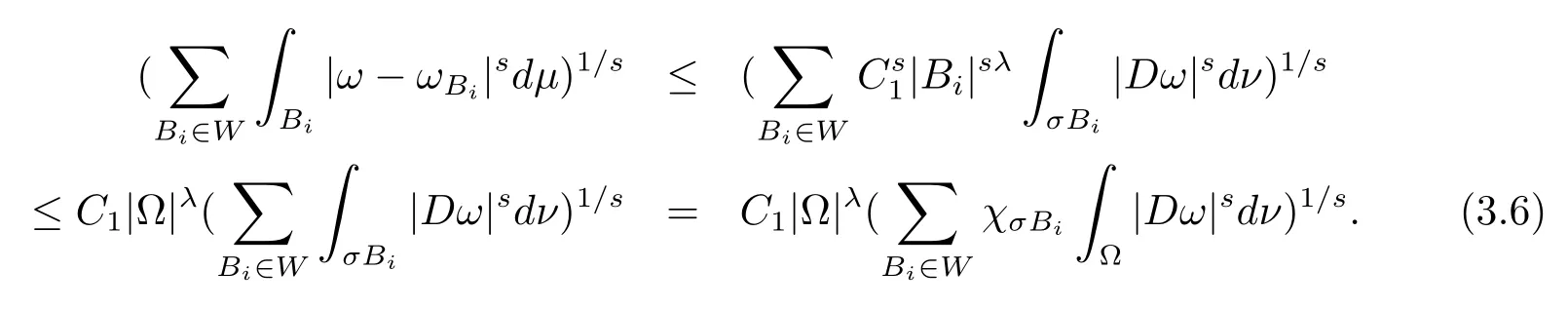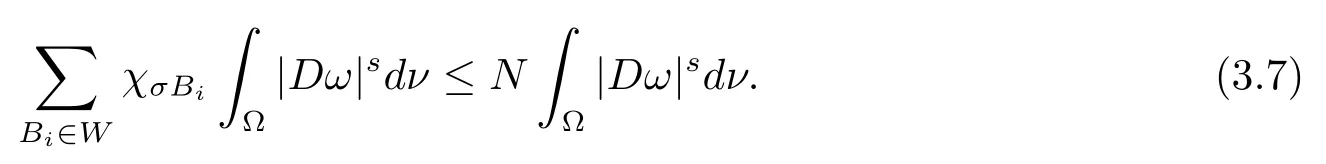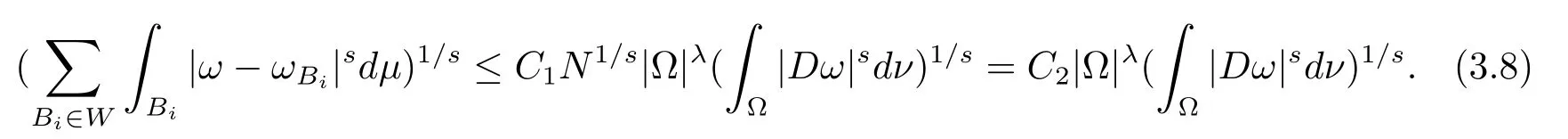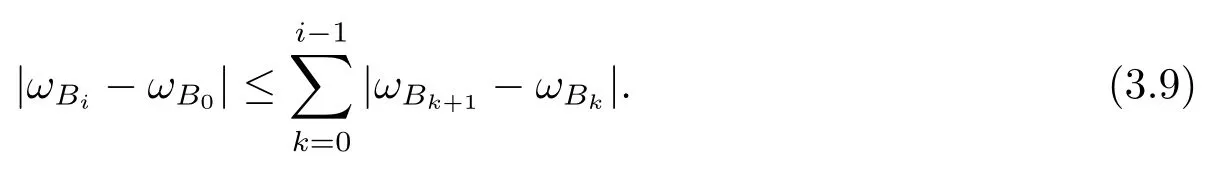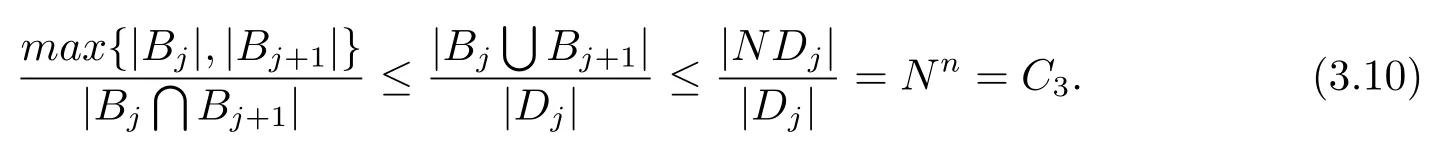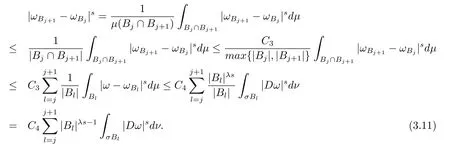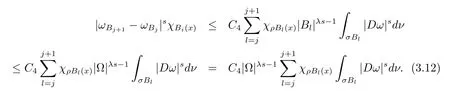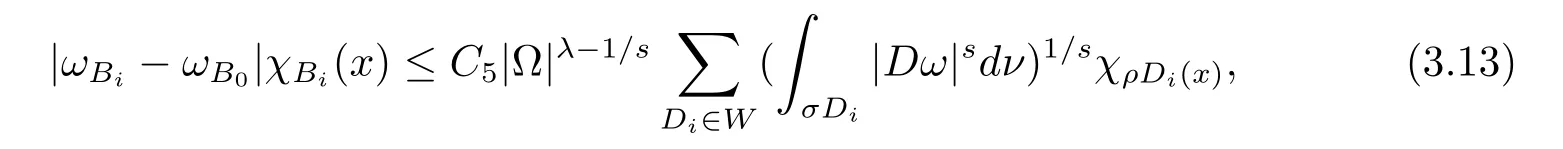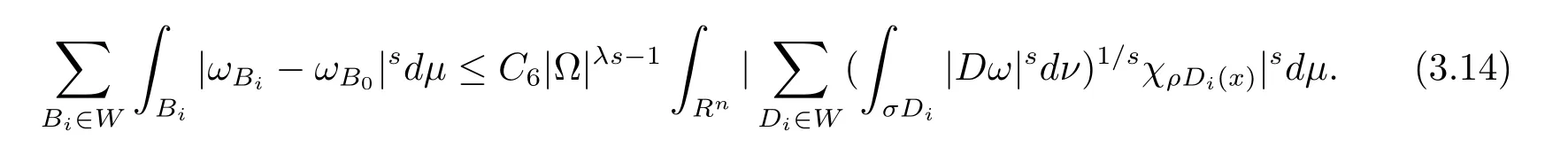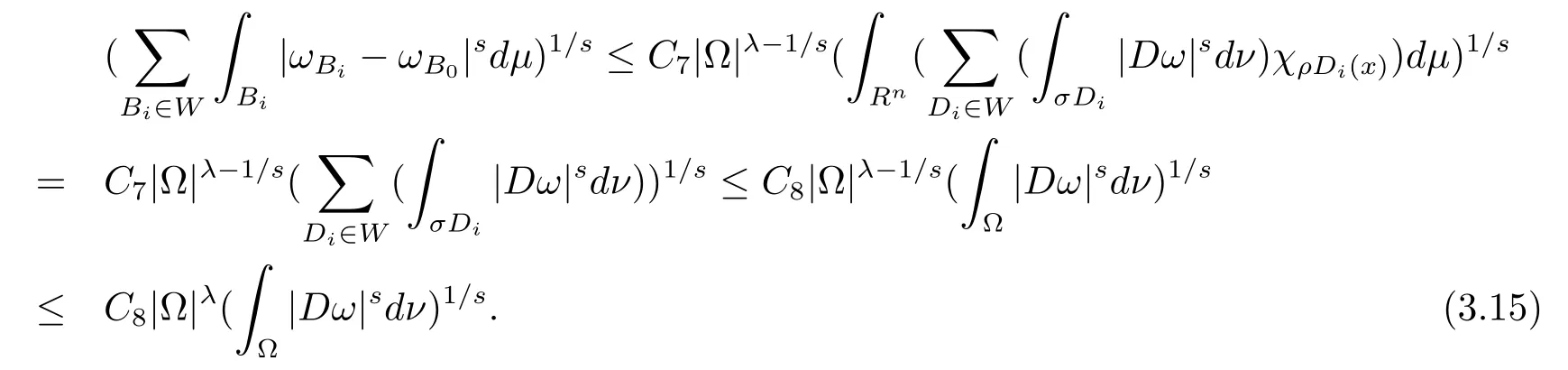关于Radon 测度的积分不等式
2019-11-23李华灿李群芳
李华灿, 李群芳
(1.江西理工大学理学院, 江西赣州341000)
(2.赣州师范高等专科学校数学系, 江西赣州341000)
1 引言
近些年, 非线性弹性理论和拟共形映射的发展促使微分形式的椭圆方程的研究取得了极大的进展, 已经从最初的Laplace 方程扩展到了A-调和方程.目前, 关于满足A-调和方程的微分形式的研究已取得较丰富的成果, 如Ding, Weisz, Liu 等数学工作者们分别做出了作用于满足A-调和方程的微分形式的Hardy-Littlewood-型、Poincar-型以及Caccioppoli-型经典积分不等式[1−5], 文献[6–9]进一步地做出了上述三类经典不等式的各类加权估计式.来源于理论物理学的Hodge-Dirac 算子, 不仅在量子力学和广义相对论中有着极为重要的作用, 还为代数学和几何学等数学分支领域的研究提供有力工具.2015 年, Ding 和Liu 在文献[10]中借助于传统的齐次A-调和方程d∗A(x,dw)=0 和Hodge-Dirac 算子得到如下形式的齐次Dirac-调和方程

其中D称为Hodge-Dirac 微分算子, 定义D=d+d∗,d是外微分算子,d∗是Hodge 上的微分算子定义为d∗=(−1)nl+1∗d∗,∗是Hodge 星算子,A是满足特定条件的算子, 更多有关Hodge 星算子∗、Hodge 上的微分算子d∗以及算子A的详细介绍可参见文献[11].作为A-调和方程的衍生方程, Dirac-调和方程的理论研究目前仍处于起步阶段, 其数学意义和实际作用还需要更深入的研究.因此, 本文将以满足Dirac-调和方程的微分形式为研究对象, 首先研究作用于其上的关于Radon 测度的局部圆域上的Poincar-型不等式, 然后以此为基础证明δ-John 域上全局的Poincar-型不等式.
本文通篇假定Ω 为Rn中的连通开子集,B为球体,ρB表示与B同心且diam(ρB)=ρdiam(B)的球体, 用|E| 来表示Rn中子集E的勒贝格测度, 文中所有积分均为勒贝格积分.设g(x)是定义在Rn上非负可积函数, Radon 测度µ由dµ=g(x)dx给出, 即µ(E)=Eg(x)dx为Rn中子集E的Radon 测度.设e1=(1,0,··· ,0),e2=(0,1,··· ,0),··· ,en=(0,0,··· ,1)为Rn上标准正交单位向量组, 用Λl=Λl(Rn) 表示由外积eI=ei1∧ei2∧···∧eil所生成的l-维向量空间, 其下标所对应的有序l-丛I=(i1,i2,··· ,il), 1≤i1 本节将在有界域上证明作用于满足Dirac-调和方程(1.1) 的微分形式的带Radon 测度的局部Poincar-型不等式, 在本节的相关证明中将用到以下重要引理. 引理2.1[10]设ω是Ω 上Dirac-调和方程(1.1) 的解,p> 1 是与方程(1.1) 有关的确定指数, 则对任意满足σB⊂Ω 的球体B, 存在不依赖于ω的常数C, 使得 成立, 其中σ>1, 0 引理2.2[10]设u∈,Λl) 是微分形式则对满足Q⊂Rn的球体Q, 有u−uQ∈Lp(Q,Λ) 且 其中C是不依赖于u与Du的常数,p>1. 引理2.3(广义Hlder 不等式) 设f,g是两个定义在Rn上的可测函数, 则对Rn中的任意子集E, 有 其中0<α<∞, 0<β<∞, 且s−1=α−1+β−1. 定理2.4设是有界域Ω 上满足Dirac-调和方程(1.1) 的微分形式,则对任一满足σB⊂Ω 的球体B, 存在不依赖于ω的常数C, 使得 上述Radon 测度µ,ν分别由dµ=g(x)dx,dν=h(x)dx定义,且其中K1> 0,K2> 0,n>α>β,σ> 1,均为常数,xB为球体B的球心. 证设rB是球体B的半径, 选取正数ε满足0<ε 不妨设球体B的球心xB为原点O(若不然, 只需将xB平移至原点O即可), 利用多重积分的极坐标变换可得 其中σ>1 为常数.综合Hlder 不等式,以及极坐标变换, 得 从而有 式(2.9) 说明式(2.1) 成立, 故定理2.4 证毕. 本节将以定理2.4 中的局部圆域上的关于Radon 测度的Poincar-型不等式(2.1) 为基础, 结合δ-John 域的相关性质, 进一步证明δ-John 域上关于Radon 测度的全局的Poincar-型不等式.在本节定理的证明中将利用下述关于δ-John 域的定义和性质. 定义3.1[12]设Ω 是Rn的一个子区域, 若存在一点x0∈Ω, 它与Ω 中任一点x均可以由Ω 中连续曲线γ连接, 且对任意ξ∈γ, 有 成立, 则称Ω 为δ-John 域, 其中δ>0,d(ξ,∂Ω) 是ξ与∂Ω 间的欧几里得距离. 引理3.2[12](覆盖引理)Rn中的每一连通开子集Ω 均有一个修正的立方体链的Whitney 覆盖W={Qi}, 且存在某常数N>1, 对所有的x∈Rn, 有 成立, 其中χ是特征函数.此外, 若则存在立方体R⊂Rn(R不必是W中的元素) 有下式成立 进一步, 若Ω 是δ-John 域, 则对于W中每一个立方体Q, 存在一中心立方体Q0∈W, 它可以通过W中立方体链Q0,Q1,Q2,··· ,Qk=Q将立方体Q连接起来, 并且有Q⊂ρQi成立,其中i=0,1,2,··· ,k−1,ρ=ρ(n,δ) 为一常数. 因为立方体与球体具有相互包含关系, 故可将引理3.2 中的立方体链{Qi} 替换为球体链{Bi}, 于是便可得到引理3.2 中关于δ-John 域的性质如下等价描述. 引理3.2设Rn中的连通开子集Ω 是δ-John 域,则存在Ω 的Whitney 覆盖W={Bi},满足下述两个条件 (1) 存在一常数N>1, 使得对所有的x∈Rn, 成立其中χ是特征函数; (2) 存在一中心球体B0∈W, 它可以通过W中球体链B0,B1,B2,··· ,Bk=B将W中任何一个球体B连接起来, 且有B⊂ρBi成立,i=0,1,2,··· ,k−1,ρ=ρ(n,δ) 为常数,并存在立方体R(R不必是W中的元素) 有下式成立 定理3.3设Ω 是δ-John 域,是Ω 上满足Dirac-调和方程(1.1) 的微分形式则存在不依赖于ω的常数C, 使得 其中Radon 测度µ,ν分别由dµ=g(x)dx,dν=h(x)dx定义且这里K1>0,K2>0,β<α 证对Ω 中任意球体B, 由g(x)≥1 可得 其中σ>1 为常数.应用初等不等式可得 其中B0⊂Ω 是满足引理中的一中心球体.由式(3.4) 可得 综合式(3.6)–(3.7), 可得 综合式(3.3),(3.10),(3.4), 便有 由β<α 其中x∈Rn.(3.13) 式两端先作s次幂, 然后在Rn上作µ-积分, 可得 综合式(3.5), (3.8), (3.15), 可得 定理3.3 证毕.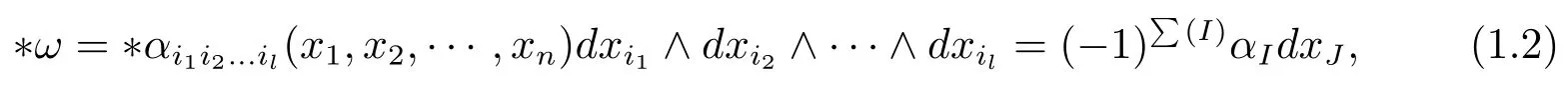
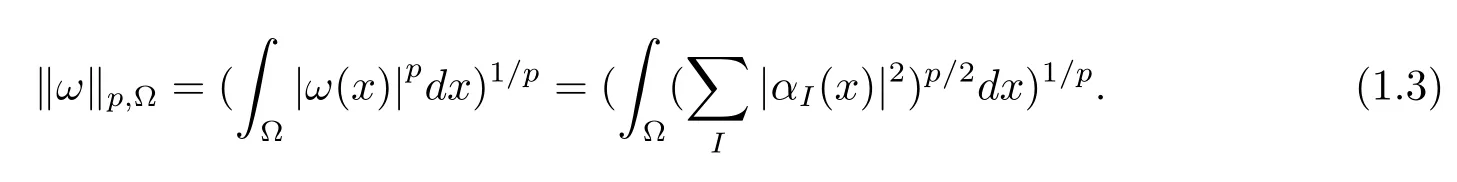
2 有界域上关于Radon 测度的局部Poincar-型不等式

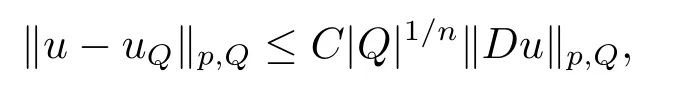
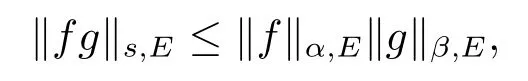
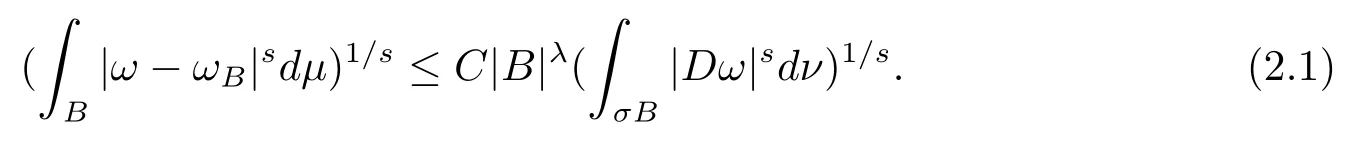
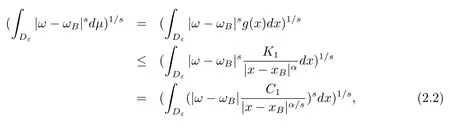



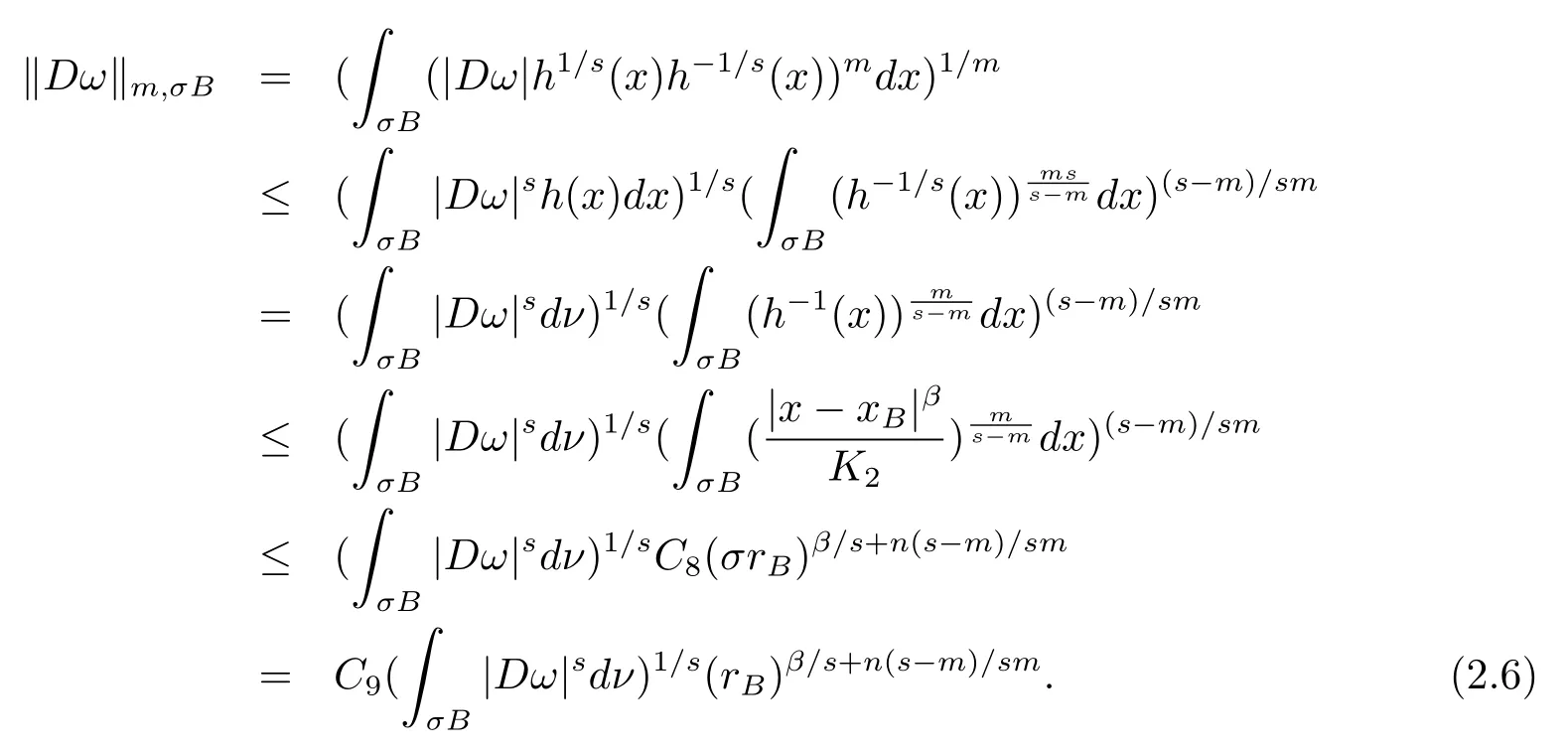

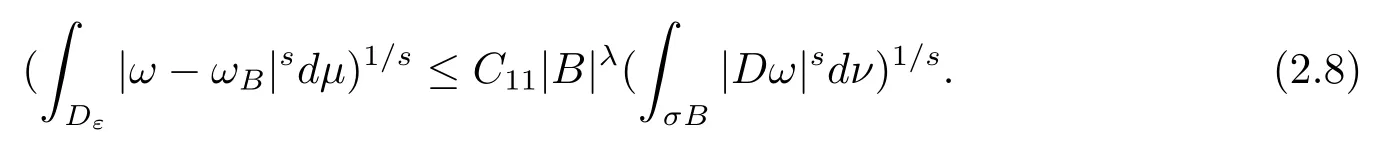
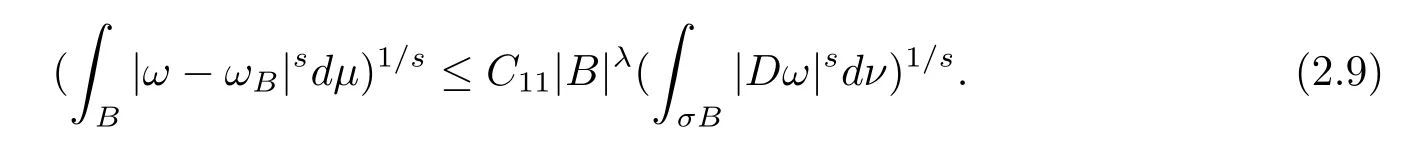
3 δ-John 域上关于Radon 测度的全局的Poincar-型不等式