Victor-Carmen 混沌系统的有限时间滑模同步

毛北行

(郑州航空工业管理学院数学学院, 河南郑州450015)

1 引言

混沌系统的同步控制逐步成为研究的热门课题[1−12], 而利用滑模控制方法研究同步逐渐成为研究不确定性系统的便捷方法, 并取得了丰富的成果.主动滑模方法, 自适应滑模方法, 积分滑模方法及比例积分滑模方法, 有限时间滑模方法, 模糊滑模等方法被相继提出.例如: 文献[13]利用主动滑模方法研究了一类混沌系统的同步控制问题, 实现了驱动响应系统的主动滑模同步控制; 文献[14]研究了分数阶Van der pol 振子网络的混沌同步; 文献[15]基于自适应滑模方法研究分数阶参数不确定系统的异结构混沌同步; 文献[16]研究Rssler 混沌系统的自适应滑模控制问题; 实现了对Rssler 混沌系统的同步控制; 文献[17]利用积分滑模滑模方法研究航天器的姿态容错控制; 文献[18]利用有限时间滑模方法研究了多涡卷混沌系统的同步.

另一方面, Victor-Carmen 混沌系统的同步激起众广大学者的极大热情, 例如: 文献[19]研究了Victor-Carmen 混沌系统的投影同步问题; 文献[20]基于自适应滑模方法研究了分数阶Victor-Carmen 混沌系统的自适应滑模控制问题.在以上研究的基础上, 研究Victor-Carmen 混沌系统的有限时间滑模同步问题, 设计新型滑模面, 能够使误差动态系统有限时间内收敛到滑模面, 较大提高了滑模同步的效率.

2 系统描述及主要结果

考虑Victor-Carmen 混沌系统[20]

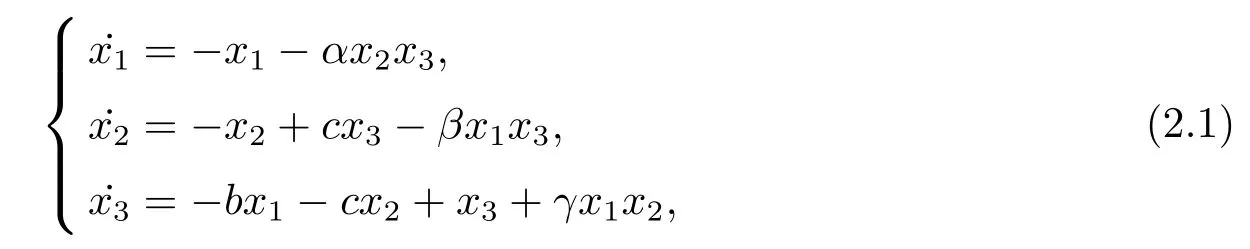
其中x1,x2,x3∈R3为状态变量;c,b,α,β,γ为常值参数.当α=50,β=20,γ=4.1,c=5,b=9 时出现怪异吸引子, 其轨相图如图1 所示.

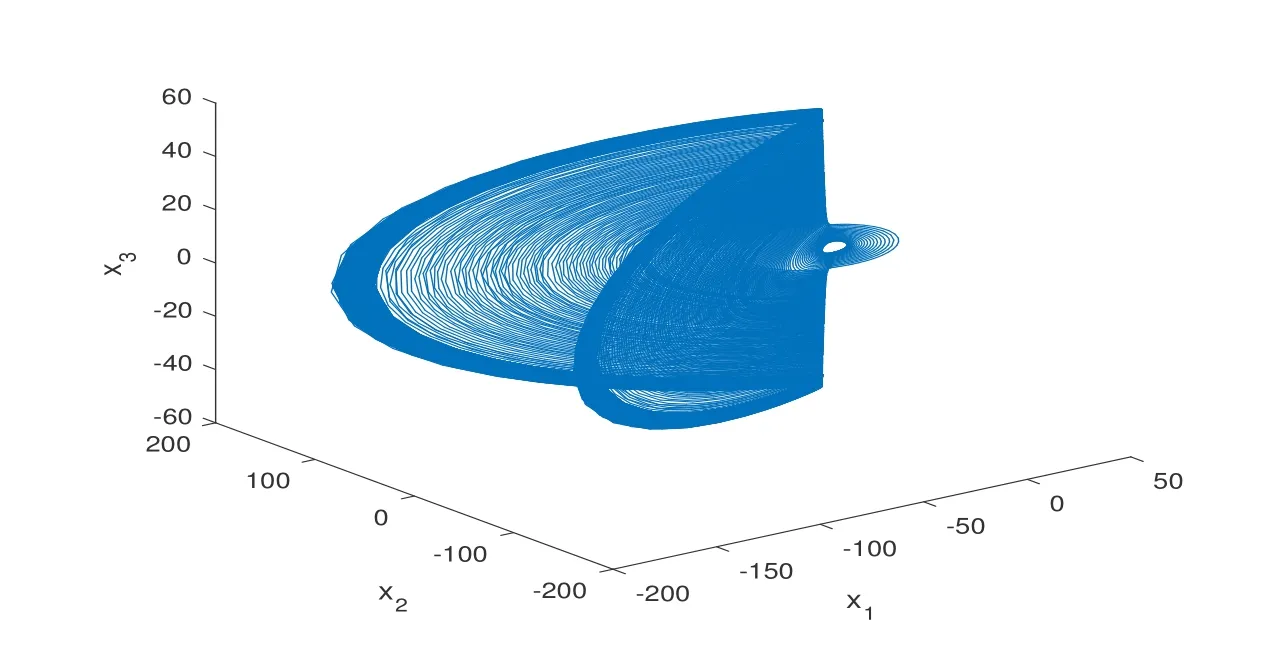
图1: Victor–Carmen 混沌系统的相轨图

从系统设计为

其中∆fi(y)(i=1,2,3) 为不确定项,y=[y1,y2,y3]T,di(t)(i=1,2,3) 为外部扰动.

假设1设不确定项∆fi(y) 和外部扰动di(t) 有界.即存在常数mi,ni>0, 使得

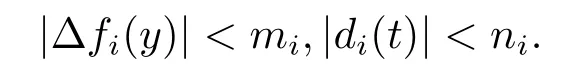
定义系统误差ei=yi−xi(i=1,2,3), 很容易得到误差方程

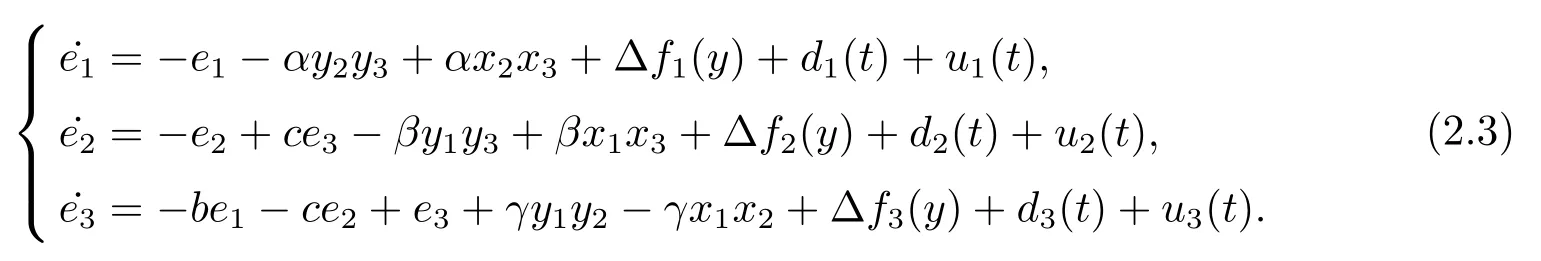
引理1[21]假设存在连续正定函数V(t) 满足微分不等式

式中p>0,0<η<1 是两个正常数.则对于任意给定的t0,V(t) 满足如下不等式

并且V(t)≡0,t≥T, 其中

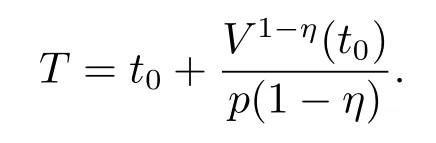
定理1在假设1 条件下, 构造滑模函数控制律

其中ki>0(i=1,2,3,4,5), 则系统(2.3) 将在时间T内收敛至切换面si=0, 其中

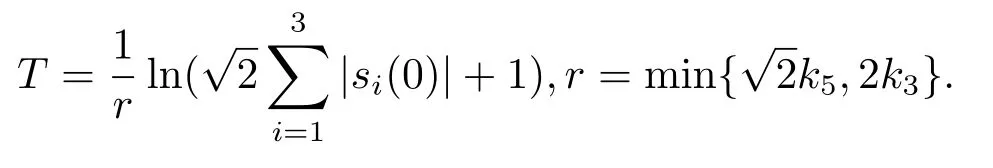
证构造函数从而得到

由引理1 滑模面具有可到达性.

定理2构造滑模函数则该滑模动态系统渐近稳定并且收敛到坐标原点, 其中

证滑模面上运动时得到

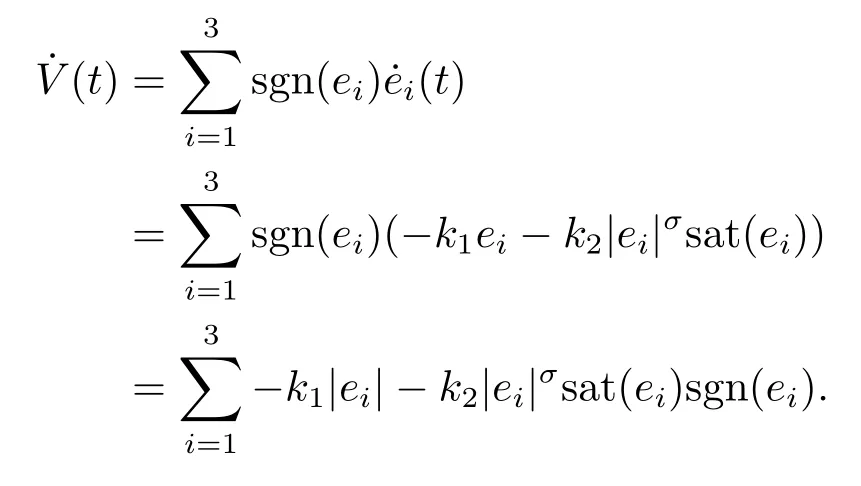
由于

定理3若满足假设1, 构造上述滑模函数和控制律, Victor-Carmen 混沌系统的主从系统(2.1) 与(2.2) 是有限时间滑模同步的.

证当不在切换面上运动时, 根据定理1 可知滑动模态系统可以被驱动到滑模面, 即滑模面具有可达性; 在切换面上时, 根据定理2 可得系统渐近稳定, 从而ei→0 , 从而具有稳定性.所以(2.1) 与(2.2) 就取得有限时间滑模同步.

3 数值仿真

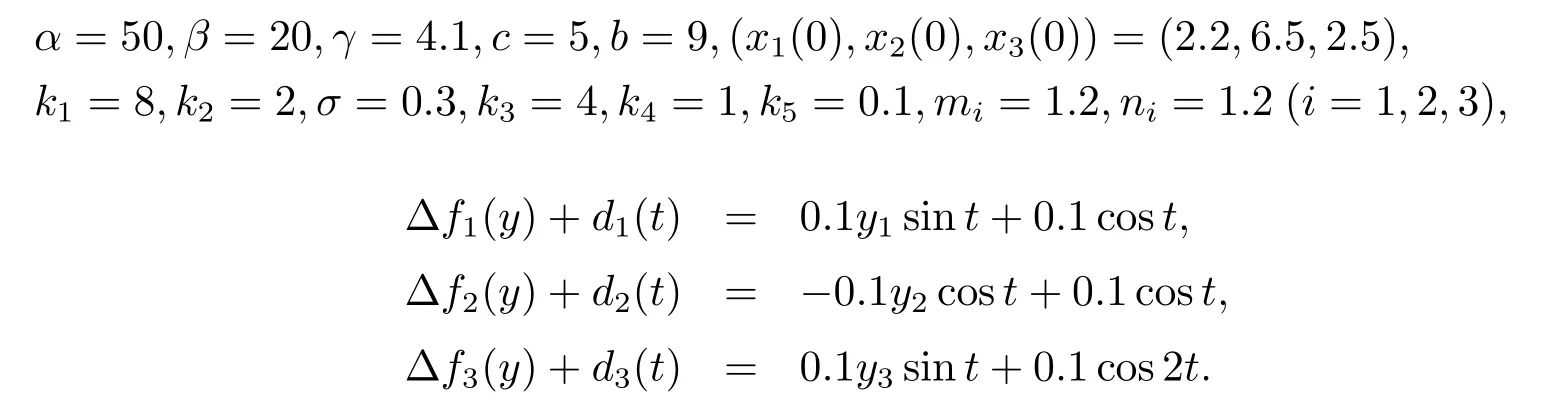
系统参数选取如上, 定理中系统的误差曲线如图2 所示, 图中可以看到, 初始时刻系统误差距离原点较远且相差较大, 随时间推移系统误差渐趋一致, 逐渐趋近于坐标原点, 表明系统取得了同步.图中看出一段时间以后系统达到混沌同步, 当时间T时刻以后, Victor-Carmen 混沌系统的主从系统(2.1)与(2.2)达到滑模同步的.时间T可由公式来推算.它给出了时刻T大小估计.若选取为传统的等速趋近律求得从而需要更长的时间才能趋于同步.

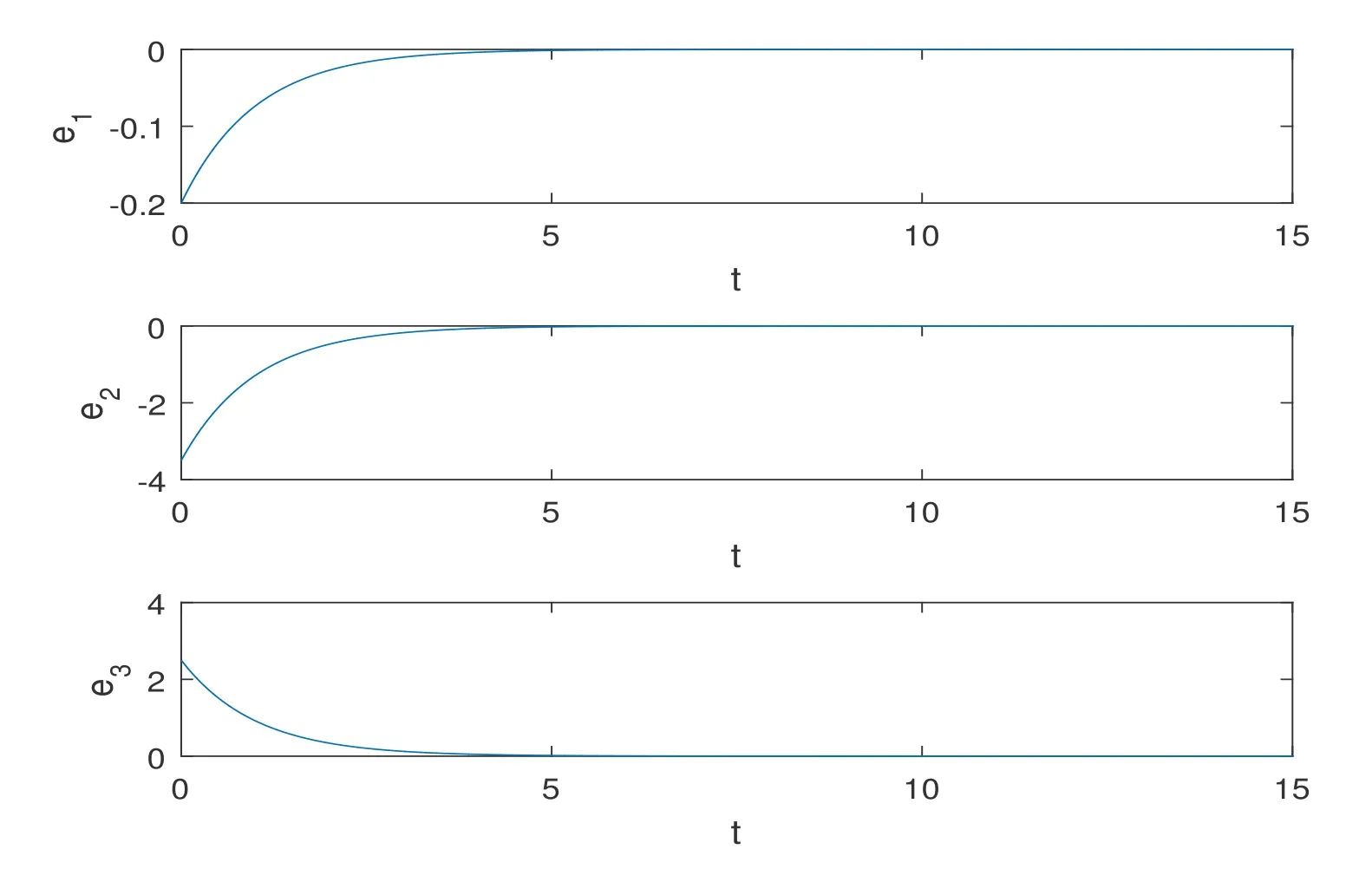
图2: 定理3 中的系统误差曲线

4 结论

基于新型滑模方法研究Victor-Carmen 混沌系统的有限时间同步, 取得Victor-Carmen混沌系统的主从系统达到有限时间滑模同步的充分条件, 从数学角度给出了严格证明和逻辑推理, 通过数值仿真检验方法的合理性和正确性.